基于共享矩阵和混沌的图像分存算法
田小平,田慧明,吴成茂
(1.西安邮电大学 电子工程学院, 陕西 西安 710121; 2.西安邮电大学 通信与信息工程学院, 陕西 西安 710121)
随着计算机技术的发展进步,信息表达形式逐渐多样化,图像信息具有较强的综合性和直观性,已成为人类表达信息的重要手段之一[1],因而有关数字图像的安全问题已经成为广泛关注的热点问题之一。迄今,研究者已经提出了多种图像加密算法[2-3],其中,Shamir[4]最早引入秘密共享的概念并给出一种门限共享方案。该方案利用拉格朗日插值将秘密值D分成n个不同的随机子秘密,只有得到不少于k(k≥n)个子秘密才能完全恢复D。进一步研究发现,秘密共享技术能够应用于视觉认证和识别[5]、离散无记忆网络[6]和数据共享[7]等各个领域。秘密图像共享方案(Secret Image Sharing Scheme,SIS)[8-9]逐渐成为数字图像加密技术中的一种重要的方法。
SIS大致分为两类,一类是视觉加密(Visual Cryptography,VC),另一类是基于多项式的秘密图像共享(Polynomial-based Secret Image Sharing,PSIS)。文献[10]给出一种独立秘密份额的VC算法,其加密效果较好,但是,重建图像质量不够理想,仅适用于二值图像且有较大的像素扩展率。文献[11]对视觉加密算法进行了改进,使用误差扩散方法,将VC算法应用到CMY彩色空间,使视觉加密算法能够运用于彩色图像。基于概率的视觉加密[12]和基于视觉加密的随机网络[13]等方法,能够有效地降低像素扩展率,这些VC方法仍然存在着一定像素扩展[14],需要花费大量的传输和存储成本。文献[15]利用分存不同图像的共享方案,虽然能够降低部分存储成本,却存在数据丢失的情况,为有损重建。为了实现无损重建,在伽罗华域(Galois Field,GF)上利用计算拉格朗日插值的方法[16]或者使用二次残差获得无损PSIS[17],而这两种方法也仅适用于固定参数的秘密共享。
目前VC和PSIS方法虽然在一定程度降低了像素扩展率和存储空间,但是,依然存在像素扩展和计算量大等问题。为了进一步提高加密性能,降低像素扩展率和存储空间,本文拟提出一种广义的基于共享矩阵与图像加密相结合的秘密图像共享算法(Combination of sharing matrix and image encryption for secret image sharing,SMIE-SIS)。首先引入一种新的(k,n)共享矩阵的概念,并分别给出构造方法及证明。再利用所构造共享矩阵的特性,将Tent混沌加密后的图像序列做行扩展后与共享矩阵进行编码后,产生秘密份额,并生成安全的多幅共享图像。
1 共享矩阵及构造方法
SMIE-SIS是利用共享矩阵对图像进行编码的一种算法。本部分分别引入一种新的共享矩阵定义,给出构造方法,再从理论上证明该构造方法所构造的矩阵满足共享矩阵的条件。
1.1 共享矩阵定义
构造参数(k,n)为正整数的n×w阶矩阵
S(k,n)=[S(k,n)(i,j)]n×w,
其中k≤n,w的大小由参数(k,n)确定,矩阵第i行第j列元素S(k,n)(i,j)∈{0,1}。随机选取矩阵S(k,n)的任意p行,构成p×w阶矩阵
Z=[Z(s,j)]p×w。
若矩阵S(k,n)和Z满足条件
(1)

(2)
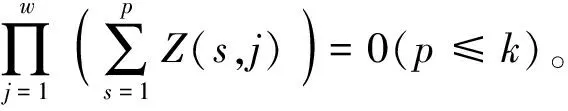
(3)
则定义S(k,n)为共享矩阵。例如,存在一个满足前述条件(1)— (3)且参数为(3,4)的共享矩阵
(4)
1.2 共享矩阵的构造方法
构造共享矩阵S(k,n)的通常方法是列出二进制矩阵所有可能的组合,并确定每一种组合是否满足共享矩阵的条件,这种方法计算复杂且运算量较大。为此,采用一种简单快速产生共享矩阵S(k,n)的方法,流程如图1所示。

图1共享矩阵产生算法
共享矩阵构造步骤如下。
步骤1初始矩阵的产生。首先,根据参数(k,n)生成矩阵元素包含(k-1)个取值为“0”和(k-1)个取值为“1”的(2k-2)×1阶矩阵,并找到所有可能的矩阵,分别记为N1,N2,…,Nl,即共有l个列矩阵,其中
将其按列组合,构成(2k-2)×l阶初始阵矩
S0=[N1,N2,…,Nl]。
(5)
步骤2根据n的值和“迭代”次数I,把矩阵S0扩展成一个新的矩阵Se。其中“迭代”次数
I=max { log2(n/(2k-2)),0}。
“迭代”方式:当n≤2k-2时,I=0,则Se=S0;当n>2k-2时,S0被“迭代”I次后扩展为矩阵Se。在第i(i=1,2,…,I)次迭代中,将矩阵Si-1在其列方向上分为列数相等的(k-1)个子矩阵,依此记为Dj(j=1,2,…,k-1)。矩阵Si-1每列上的第j个矩阵元素“1”被第j个子矩阵Dj的矩阵元素所替换,其余位置的“0”被矩阵元素全为“1”的同阶子矩阵元素所替换。直到完成“迭代”,最终扩展为一个新的矩阵,记为Se,显然,Se是2I(2k-2)×Ne阶矩阵,其中Ne=lI+1。
步骤3在所扩展的矩阵Se中,随机选取其n行,即得到一个参数为(k,n)的n×Ne阶共享矩阵S(k,n)。
以构造共享矩阵S(2,3)为例。确定矩阵Ni的数目l=2,“迭代”次数I=1。按前述步骤可得
(6)
(7)
(8)
可以证明,依前述构造方法所得矩阵满足共享矩阵的3个条件。
考虑到(2k-2)×l阶的初始矩阵S0由矩阵Ni组成,矩阵S0每行中矩阵元素“1”和“0”的数目相同,且均为l/2。当k≥2时,可得
因此,在矩阵S0中的每一行都至少有一个取值“1”矩阵元素,满足条件(1)。
考虑到S0每列包含(k-1)个取值为“1”和(k-1)个“0”的矩阵元素,任取S0中的p行,当p≥k时,每列中“1”的个数为
o-(k-1)=p-k+1≥1,
即满足条件(2)。
当p≤k-1时,至少有一列矩阵元素全为“0”元素。由于每列取值为“0”的矩阵元素总数为(k-1),所以,选取不大于(k-1)行矩阵,至少有一个列矩阵元素全为“0”,亦满足条件(3)。
从矩阵S0扩展为矩阵Se时,每列矩阵元素添加了更多取值为“1”的矩阵元素,而取值为“0”矩阵元素个数仍然为(k-1)。矩阵Se也可以看作是其第一列元素全部可能的排列组合所构成的矩阵,则每行取值为“0”的矩阵元素个数为(l/2)2。考虑到I≥1,l≥2,因此,矩阵Se每行中“1”的个数为
lI+1-(l/2)2=≥3,
即在Se中任取k行所得矩阵Sk每行至少有3个取值为“1”的矩阵元素,显然,Se满足条件式(1)。
在矩阵Sk中任取p行得到矩阵Z。如果p=k,矩阵Z中每列矩阵元素至少含有1个取值为“1”的矩阵元素,不多于(k-1)个取值为“0”的矩阵元素。如果p≤k-1,每列中取值为“0”矩阵元素个数最多为(k-1),矩阵Z中至少有1列全为“0”,满足条件(2)和条件 (3)。
综上所述,按照共享矩阵构造方法所得矩阵Se满足共享矩阵条件。
2 共享编码与解码
本部分将利用所引入的共享矩阵的特性,对图像数据进行加密与重构,分为共享和重建两个过程完成。
2.1 共享过程
共享过程是利用所构造共享矩阵S(k,n)对图像数据矩阵P进行分享。
首先,对图像数据矩阵P进行行扩展得到矩阵
A1(i,:)=P(i=1,2,…,n)。
(9)
其中P为1×w阶矩阵。
然后,对矩阵A1进行分享运算,可得秘密份额矩阵
R=A1*S(k,n)。
(10)
式中运算符“*”表示两矩阵对应位置元素相乘。
例如,取图像数据矩阵
P=[1,23,128,32,8,45],
共享矩阵取式(4)所示的S(3,4),那么有
(11)

(12)
矩阵R中每一行形成一个秘密份额,则形成4个不同的秘密分享分存在不同接收者。
2.2 重建过程
重建过程是利用共享矩阵把秘密份额恢复为原始数据的过程。首先产生一个与矩阵R同阶的矩阵Rm,其中Rm有kr行矩阵元素取值均为“1”,其余行矩阵元素取值为“0”,其中kr为任意选取矩阵R的行数。
然后,利用矩阵Rm产生矩阵
R1=R*Rm=A1*S*Rm,
(13)
和重建矩阵Rr=[Rr(j)]1×w,其中
Rr(j)=R1(1,j)‖R1(2,j),…,‖R1(n,j)=
(A1(1,j)*S(1,j)*Rm(1,j))‖(A1(2,j)*
S(2,j)*Rm(2,j)),…,‖(A1(n,j)*S(n,j)*Rm(n,j))=
(P(j)*S(1,j)*Rm(1,j))‖(P(j)*
S(2,j)*Rm(2,j)),…,‖(P(j)*S(n,j)*Rm(n,j))=
P(j)*[(S(1,j)*Rm(1,j))‖(S(2,j)*
Rm(2,j)),…,‖(S(n,j)*Rm(n,j))]=
P(j)*Rs(j)
(14)
其中
Rs(j)=[S(1,j)*Rm(1,j)]‖[S(2,j)*
Rm(2,j)],…,‖[S(n,j)*Rm(n,j)]
(j=1,2,…,w),
(15)
符号“‖”表示十进制按位异或运算。
根据式(2)可知,如果kr≥k,共享矩阵每列至少有一个取值为“1”的矩阵元素,显然,对于每个给定的j,必有一个矩阵元素满足
S(i,j)*Rm(i,j)=1(i=1,2,…,n)。
所以
Rs(j)=1,Rr(j)=P(j),
表明重建矩阵Rr与原始数据矩阵P相同。
根据式(3)可知,当kr S(i,j)*Rm(i,j)=0(i=1,2,…,n), 所以,至少存在一个Rs(j),从而导致 Rr(j)≠P(j)。 采用式(12)数据,分别选取2个和3个秘密份额的两种情况,以说明计算过程。选取2个秘密份额的重构过程描述如下。 依据式(14)可得6个重构数据份额分别为 同理,选取3个秘密份额的重构过程分别如下。 根据式(14)可得4个重构数据份额分别为 因为共享矩阵中参数k=3,n=4,故选取2个秘密份额不能完全恢复原始数据,而选取3个秘密份额能完全恢复原始数据。 根据混沌系统和共享矩阵的特性,给出SMIE-SIS算法。利用混沌系统将原始图像变成与噪声类似的随机序列,并将“密钥”隐藏在序列中,再利用共享矩阵对混沌加密图像进行点积编码。 混沌系统是图像加密的一种有效工具,考虑到帐篷映射(tent map)[3]是典型的二维混沌系统,其参数少且鲁棒性好等优点。为此,本文利用它产生随机序列实现图像像素扩散加密,提高图像分存共享的安全性,在使用过程中也可以用其他混沌系统进行混沌加密。 将大小为W×L的原始图像转变为一维数据矩阵U,利用随机数产生长度为192的密钥 K=(k1,k2,…,k192), 其中ki∈{0,1}(i=1,2,…,192)。 利用密钥K产生Tent混沌序列的两组初值(r1,C1(1))和(r2,C2(1)),其中 (16) (17) 其中x=1,2,且 将式(16)和式(17)所得到混沌序列初值代入 (18) 式中y=1,2,…,(W×L)。利用C1序列,先把一维数据U加密为数据 (19) 然后,将数据E1(y)加密为数据 (20) 将加密数据E2和密钥K结合成最终加密数据 E=[KS,E2]。 (21) 其中KS=〈K⊕‖∑E2‖〉,“⊕”表示二进制按位异或运算,‖x‖定义为将十进制数转变为二进制数,且总比特位应与秘钥的总长度相同,且为192 bits。〈x〉定义运算为把二进制数转为24个十进制数,每个十进制数包括8个比特位。因此,加密数据E阶为1×(W×L+24)。 共享矩阵对混沌加密数据进行共享编码,产生最终的分存加密图像。 利用共享矩阵的产生方法得到共享矩阵S(k,n),把矩阵S(k,n)重复列扩展,使最终扩展为n×(W×L+24)阶矩阵。按照式(9)和(10)编码方式,对数据E进行编码。可以看出,对于E中每一个元素,如果其共享矩阵的对应位置矩阵元素为“1”,则使E中该位置元素保留,如果共享矩阵该位置矩阵元素为“0”,则E中该位置元素被删去,最终编码后得到了一个降阶矩阵,记为Hi,其中i与共享矩阵的参数n选取有关。可以看出,降阶后矩阵实现数据量至少减半。 将共享矩阵的信息融合在矩阵Hi中,得到融合信息数据列矩阵,记为Fi。其融合方式为 Fi=[D,B,Hi]。 (22) 式中D,为1×2阶的矩阵,与Ne有关,其表示式为 (23) D(2)=Nemod 256。 (24) (25) (26) 最后,将列矩阵Fi转换为矩阵 (27) 其中qi为每个Fi中矩阵元素素个数;01×v是1×v阶的全零矩阵,且v=f(qi,W)。 图像重建是图像加密的逆过程,要完全的恢复原始图像,用户需要接收到任意kr(kr≥k)个秘密共享图像。 将每个秘密共享图像转变为一维数据矩阵,把一维数据矩阵分为三部分。 1) 矩阵序列的前两个数为第一部分,按照式(23)—(24)得到Ne的值。 3) 除去矩阵中第一、二部分的元素为第三部分,记为矩阵Hd。 利用恢复的共享矩阵和式(14)—(15)重构方式将Hd重构为矩阵Ed。把矩阵Ed分为两部分,前24个矩阵元素素为第一部分记为矩阵Ks,其余矩阵元素素为另一部分记为E2。 从矩阵Ks提取密钥K,其提取方式为 K=‖Ks‖⊕‖∑E2‖。 (28) 然后利用式(16)—(18)产生混沌序列C1和C2,利用序列C2将E2恢复为数据E1,其中 (29) 其中如果-256≤E1(i)<0,则E1(i)+256;如果E1(i)<-256,则E1(i)+2×256。 再利用C1将E1恢复到原始数据U,其中 (30) 其中如果-256≤U(i)<0,则U(i)+256;如果U(i)<-256,则U(i)+2×256。 为了验证算法的有效性和鲁棒性,在Matlab.R2014.a平台上分别对灰度、二值和彩色等3种图像进行测试。 取不同的(k,n)参数,对不同的图像种类进行仿真分析,结果如图2—图4所示。图2(a)为原始灰度图像其大为256×256,图2(b)—(e)为使用(3,4)共享矩阵产生4个不同的秘密共享图像,且大小为都为256×129。图2(f)—(g)为分别选择秘密共享中的任意2个和3个份额重建的结果。图3(a)为原始二值图像其大为256×256,图3(b)—(g)为使用(4,6)共享矩阵产生6个不同的秘密共享图像,且大小为都为256×129。图3(h)—(j)为分别选择秘密共享中的任意2个、3个和4个份额重建的结果。图4(a)为原始彩色图像其大为256×280×3,图4(b)—(i)为使用(5,8)共享矩阵产生8个不同的共享秘密图像,且大小为都为256×141。可见,加密数据与原始数据相比,数据量减半。图4(j)—(m)为分别选择秘密共享中的任意2个、3个、4个和5个份额重建的结果。 图2 灰度图像测试结果 图3 二值图像测试结果 图4 彩色图像测试结果 由图2、图3、图4可见,该算法适用于不同种类图像,通过设置不同参数,能得到不同数目的秘密共享图像。在重建图像中,要选取不少于k个秘密份额才可以完全恢复原始图像。 对SMIE-SIS算法进行秘钥空间分析,其密钥空间是由192个随机数来决定的,故其密钥空间为2192,远大于2100的基本密钥空间要求[18]。由于是随机的密钥,使得即使输入相同,每次将也会产生不同的加密结果,如图5所示。这个性质克服了许多现有图像加密方法的缺点,使其能够抵抗密码分析攻击[19]。 针对秘钥空间大小,给出证明 (31) 因为Enc(o,k)=e,所以 P(E=e,O=o)=P(K=k,O=o), (32) 又因K和O相互独立,所以 P(E=e,O=o)=P(K=k,O=o)= (33) (34) (35) (36) 其中P表示成功攻击的可能性,Enc表示加密过程Sharing表示的是共享过程,且加密结果e∈E,原始图像o∈O。 根据式(35)—(36)可得在加密和共享编码过程中成功攻击的可能性为 P(Encbreak)=2-192, (37) P(Sharingbreak)=256-(1+WL/2)。 (38) 如果实验中图像大小为256×280,其成功攻击的可能性为 P(Sharingbreak)= (39) 由式(37)—(39)计算可得本文算法被成功攻击的可能性为2-286 920,是几乎不可能被攻击,故本文算法具有较高的安全性。 图5 相同图像的不同秘钥加密结果 对图2中原始图像和加密图像进行直方图分析,如图6和图7所示。 由图7可以看出,每个密文图像的直方图形状几乎一样且每个灰度值大致呈均匀分布,说明该算法对明文置乱效果较好。 图6 原始灰度图像直方图 图7 灰度图像加密直方图 对明文中特定位置不同像素块经加密后的比较进行差分攻击,测试结果如图8所示。其中原始图像大小为256×256,初始参数(k,n)=(3,4)。 图8 差分攻击测试图 图8(a)为原始明文图像,图8(b)为差分攻击(a)中(50,150)位置的像素后的图像,且他们的差值图像如图8(c)所示。图8(d)—(g)为原始明文图像加密后的秘密份额。图8(h)—(k)为明文攻击图像加密后的秘密份额。图8(l)—(p)为原始图像密文和差分攻击图像密文的差值显示。实验可知,差分攻击明文的加密图像与原始明文的加密图像相差很大,接近于噪声序列。说明该算法能够抵抗差分攻击。 暴力攻击的好坏是图像加密算法的另一种体现。对秘密共享份额施加暴力攻击的结果如图9所示,其中原始图像大小为256×256,初始参数(k,n)=(4,6)。图9(a)—(d)为四个原始的秘密份额,图9(e)为攻击(d)中(80,80)位置的像素后的秘密份额。图9(f)为错误份额和正确份额的差值。 图9 暴力攻击测试图 由图9可知,把攻击密文图9(e)与图9(a)—(c)重构图像时,未能成功重建图像,如图9(g)所示。仅当四个或更多秘密份额正确接收,接收者能够成功重建原始图像,如图9(h)所示。正确猜测一个共享份额中所有像素值的概率为2-256×256,这几乎是不可能的,表明提出的SMIE-SIS算法可以抵抗暴力攻击。 信息熵可以反映数字图像中像素灰度值的分布状态。像素灰度值分布越均匀,信息熵越大,对于理想的随机图像,所有灰度级出现的概率相等。在这种情况下,信息熵的值达到最大值,且为 因此,有效的加密算法应使信息熵尽可能达到最大[20]。信息熵定义为 (40) 计算图4—6中各参数下不同种类图像的信息熵值,如表1所示。 表1 信息熵(平均值) 单位:bit 由表1可以看出三种图像的秘密分享图像的信息熵都接近理论的最大值,说明其加密效果较好。从未成功重建图像的信息熵中,可以看出他们的值也接近理论的最大值,表明未成功重建图像的像素值随机分布,没有原始信息泄漏。 针对VC和PSIS算法存在的安全性差和像素扩展率大等问题,给出一种共享矩阵与混沌图像加密相结合的图像分存方法。通过二值、灰度和彩色图像的测试表明,SMIE-SIS算法的秘密共享图像是均为原图像的一半,有效的缩小了像素比和存储空间;同时,SMIE-SIS能够抵御暴力攻击,差分攻击和检测假的共享份额,具有较强的鲁棒性。鉴于所提算法具有秘密分存算法的特性,且能够有效的降低存储和传输成本,因此,将该算法可以应用于数字签名、视觉认证以及现代加密体制等领域。3 共享矩阵混沌加密算法
3.1 混沌图像加密
3.2 加密图像共享编码
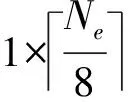


3.3 图像重建
4 实验结果和分析
4.1 测试结果



4.2 密钥空间分析
P(K=k)P(O=o),
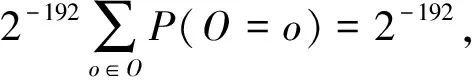

P(Encbreak)P(Sharingbreak)=
2-192256-(256×280/2)=2-286 920。
4.3 灰度直方图分析
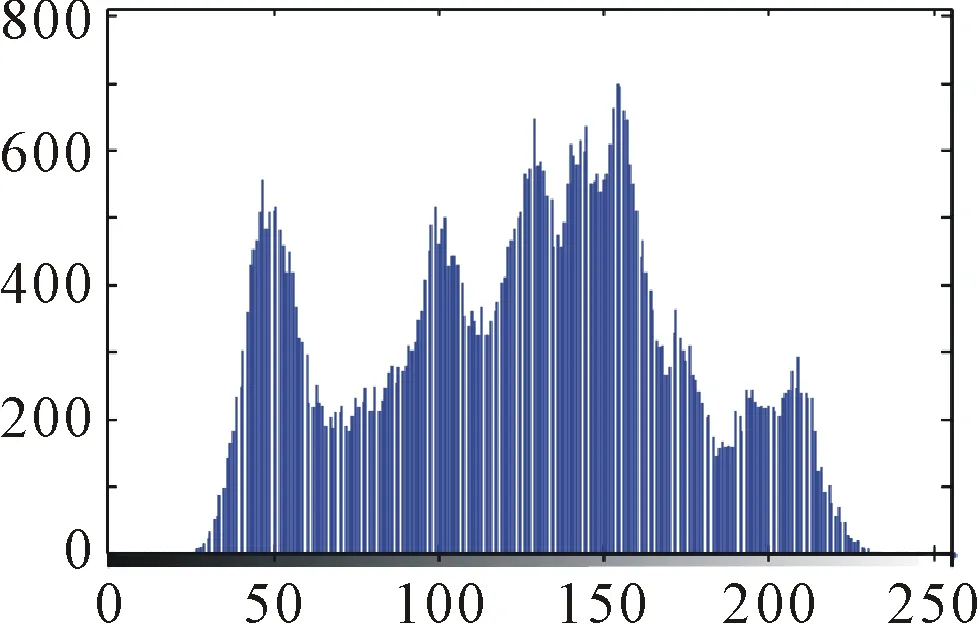

4.4 差分攻击分析

4.5 暴力攻击分析

4.6 信息熵分析


5 结束语

