皮尔士存在图直观性辩护

程　橙

(中国人民大学 哲学院，北京 100872)

1896年末，时年57岁的皮尔士于创立了存在图系统(the system of existential graph，简称EG)。在随后的十几年中，他全身心地投入到存在图研究中，发现它与模态理论、符号理论、范畴理论和实用主义哲学密切相关①Robert,Don D.The Existential Graphs of Charles S.Peirce.Netherlands:Mouton & Co.N.V.,Publishers.1973:p.12.。1905年和1908年，他宣称存在图是他的“杰作”②Peirce,Charles S.Collected Papers of Charles Sanders Peirce.Vol.4.Edited by Charles Hartshorne,Paul Weiss,and Arthur Burks.Cambridge,Mass:Harvard University Press.1934:p.291.。存在图理论遭受了诸多质疑，进展面临着困难与挑战。学者们的质疑大体可以分为两个方面，一方面认为存在图的表达力不足，另一方面则认为存在图不够精确，容易导致模棱两可的解读。最终，提出如此质疑的学者们大多都表示出了对代数逻辑的偏好。而对存在图理论的辩护也从未停止。尤其是20世纪60年代以来，随着计算机技术和认知科学的发展，越来越多的学者重新拾起对图式化推理的兴趣。约瑟夫·泽曼、丹·罗伯茨等人的成果有力地反驳了来自上述两个方面的质疑。首先，和相应的代数逻辑系统的同构性表明，存在图系统的表达力并不逊色。其次，在加入了一些辅助装置和新的变形规则之后，存在图能够有效地避免被误读，其精确性得到了保证。然而，旧的问题解决了，新的问题随之而来。为了增强其表达能力而介入了越来越多的数理逻辑的方法，损害了存在图的在演算方面的直观性。图式逻辑的优势就是证明的直观性，所以，失去了直观性也就失去了优势，于是，重新树立直观性成为图示逻辑研究领域内亟待解决的问题。

一、断言页：涵义与事实

无论是图式逻辑还是代数逻辑，作为表达系统，都不能在推理中运用偶然性质(accidental properties)，因此必须区分语法和语义。例如，在图式逻辑中封闭曲线的大小、形状和线的长短、粗细是偶然性质，也需要对其作出区分，从而制定能指与所指之间的对应关系。如果将偶然性质误当作事实进行推理，势必导致错误。

从语义学角度来解释存在图的直观性是必要的。皮尔士说，存在图的作用在于促进对逻辑结构的分析，而非运算③Peirce.Collected Papers of Charles Sanders Peirce.vol.4.p.373.。蒯因也认为，在分析方面，皮尔士的图式逻辑方法可能比代数逻辑方法更具优势④Quine,W.V.O.“The Simplest Mathematics”,Review of the Collected Papers of Charles Sanders Peirce(Volume 4),Isis 22,p.551-553.。首先，皮尔士将句子与命题看作等同的，能够表达某部分理念(idea)的断言(assertion)，并且这部分理念是通过永恒的、合情合理的事实或法则表现出来的①Peirce.Collected Papers of Charles Sanders Peirce.Vol.3.1933:p.291.。其次，他提出同一个断言能够被两个不同的，但却拥有着相同涵义的句子/命题所表达②Peirce.Collected Papers of Charles Sanders Peirce.Vol.4.1934:p.300,p.331,p.375,p.399,p.346-347.。再次，皮尔士在句子/命题的基础上创造出新概念——断言页(the sheet of assertion)，专门用来表达“真”的语义世界。从此，想表达句子/命题的真值就不必另引入一套语义系统，而是直观地展现在读者面前——“真”即为所见。需要注意的是，后来皮尔士偏向于使用“命题”这个称呼，所以下文中的“皮尔士命题”即指代命题又指代句子。

断言页的定义是，“一张纸，一块黑板，或者一面墙都可以被称作断言页，用以表示论述组成的世界。”③Peirce.Collected Papers of Charles Sanders Peirce.Vol.4.1934:p.300,p.331,p.375,p.399,p.346-347.皮尔士把任何可以写写画画的地方都称作断言页。一般地，我们把断言页看作一张白纸。凡是写在这张白纸上的肯定命题和否定命题其真值都为真(被“切”，即“封闭曲线”，包围的皮尔士命题为否定命题，未被封闭曲线包围的皮尔士命题为肯定命题)④⑤Peirce.Collected Papers of Charles Sanders Peirce.Vol.4.1934:p.300,p.331,p.375,p.399,p.346-347.。当皮尔士把命题写在断言页上的时候，我们就称由该断言页和命题共同构成的整个区域为“图”⑥Peirce.Collected Papers of Charles Sanders Peirce.Vol.4.1934:p.300,p.331,p.375,p.399,p.346-347.。该图的表达力很强，能够表达陈述世界中不同的可能世界的情况(见本文第三节)。

itrains

图1肯定命题的存在图案例

图2否定命题的存在图案例

弗雷格对语句(sentence)的定义是，语句是具有真值的函项表达式。弗雷格把函数概念在语义学和哲学中进行推广，提出了“函数(函项表达式)总能表达成一个概念(语句)，概念是其值总为真值的函数”⑦[德]弗雷格：《函数与概念》，《弗雷格哲学论著选辑》，王路译，北京：商务印书馆，2006年版，第63页。的观点。弗雷格的推广对罗素的影响深远。罗素说：“函数概念不必限于数学，或者限于数学家使我们习知的用途；它可以推广到所有一对多的关系的情形，‘x的父亲’是一个以x为变目的函项，它和‘x的对数’同样是个合法的函项。这种意义上的函项是摹状函项。以后我们将见到一种更普遍、更基本的函项，即命题函项。”⑧Russell,B.“On Propositions:What They Are and How They Mean”,in Proceeding of the Aristotelian Society,Supplementary Volumes,Vol.2,Problems of Science and Philosophy,1919,2(Jul):p.46,p.28.从罗素的这段话中我们看到，命题(proposition)是被赋值的命题函项。需要特别注意的是，罗素所说的命题函项就是开语句，开语句也就是函项表达式，其区别在于赋值之后的命题函项是命题，其值是命题，而赋值之后的函项表达式是语句，其值是真值。随后，罗素又提出：“一个命题是一个信念的内容”，“有一个由意象组成的复合事实，它有一个类似于使这个信念称为真实的客观事实的结构”⑨Russell,B.“On Propositions:What They Are and How They Mean”,in Proceeding of the Aristotelian Society,Supplementary Volumes,Vol.2,Problems of Science and Philosophy,1919,2(Jul):p.46,p.28.，罗素认为信念不是语言成分，而是心理成分，因此，罗素对命题的解释在心理主义的立场上与弗雷格的反心理主义立场背道而驰。

罗素的命题对应于弗雷格的语句，意象对应于涵义，客观事实对应于真值⑩陈晓平：《罗素的命题与弗雷格的语句之比较》，《哲学研究》，2012年第4期。。由此，我们可以将弗雷格语句与罗素命题的异同总结为如下三点：

1.语句和命题都是陈述句。

2.语句的指称是真值，命题的指称是客观事实。

3.语句的涵义是反心理主义的，命题的意象(组合)是心理主义的。

将断言页与命题和语句进行横向比较，断言页的特点可以被总结为如下三点：

a.表达陈述性的皮尔士命题。

b.不同的皮尔士命题可以构成不同的存在图；如果表达了相同的涵义，那么就指向同一个事实，可以进行替换。如果表达了不同的涵义，则指向不同的事实，不可以进行替换。但是，这两个事实可以(通过并列关系)组成一个新的事实。

c.真命题直观地展现在读者面前——“真”即为所见，即为事实。

由此可见，断言页在意象与涵义的对立中选择了涵义以及涵义的反心理主义立场，而在事实与真值的对立中选择了事实。这样，即避免了罗素的关于(带有主观色彩的)意象的含混不清的解释，又避免了弗雷格在涵义不等式问题和从句真值替换问题中遇到的困境。

罗素的关于(带有主观色彩的)意象的含混不清的解释：“命题和它的意象(objective)之间的关系并不是想象之物和事实之物之间的关系，而是两个同样可靠的事实之间的关系。其中，命题由图像(images)和可能的混合的感觉组成。”*Russell，B．“On Propositions: What They Are and How They Mean”: p.30．罗素把命题看作事实，而作为事实的命题有真有假，其真假取决于命题和意象之间的一致性。首先，由图像和可能的混合的感觉组成的命题何以成为事实？其次，既然命题是事实而命题又有真有假，那么“假的命题”即“假的事实”何以存在？

弗雷格在涵义不等式问题和从句真值替换问题中遇到的困境：按照弗雷格的涵义与指称理论，22=4和2>1的真值相同，可以组成一个等式。但是，(22=4)=(2>1)这个等式是违反常识的，因为它不符合人们的直观需求。直观上，人们需要等式两边不仅指称相等，而且涵义也相等。为了辩护自己的涵义与指称理论，弗雷格提出，人们这种“等式两边既要指称相等，又要涵义相等”的直观需求是不恰当的——如果人们不要求24=42这个等式的两边的涵义相等，那么就不应该要求(22=4)=(2>1)这个等式的两边涵义相等。另外，在直接语境中，任何两个同真或者同假的语句可以相互替代而不改变由以组成的复合句的真值。但是，大多数主从复合句不能进行基于从句真值相等的保值替换，这就是为何他不得不把大多数主从复合句解释为间接语境或者其他某种非直接语境的语境。

直观是人们的习惯。符合直观就是符合人们的认知习惯。有的习惯符合事实，有的习惯不符合事实，需要在实践中进行筛选，无论走过多少弯路最终人们会在现有的认知水平内形成一样的习惯，这就是皮尔士实用主义的主旨。

二、同一线与切的空间关系：直观化的关系逻辑

从关系逻辑的角度来解释存在图的直观性是必要的。首先，关系逻辑是皮尔士最重要的贡献之一，他发展了德·摩根的思想，在逻辑史上第一次全面系统地建立了关系演算。其次，皮尔士在多篇文章中尝试用画图的方式表现个体之间的关系，从作为过渡阶段的实体图(Entitative Graphs)到作为最终成果的存在图(Existential Graphs),“关系词(relative)”是理解皮尔士逻辑思想的重要角度。再次，从关系逻辑的角度研究存在图的直观性的文章还很少，本节愿意做一些初步尝试。

在关系逻辑理论中，所有的逻辑词项都被解释为关系词。关系逻辑理论的主要内容有：关系词的定义。从关系的定义可以看出，皮尔士认为关系词优先地带有镜像，或者图像性质：一个关系词仅仅是一个镜像(icon),一个图像(image),与经验无关……但是隐含着对附属性(attachments)的需求①Peirce.Collected Papers of Charles Sanders Peirce.Vol.3.1933:p.290.。关系词的分类。绝对词(一元关系词)，简单关系词(二元关系词)和结合词(三元及以上关系词)②张家龙：《数理逻辑发展史——从莱布尼茨到哥德尔》，北京：社会科学文献出版社，1993年版，第95页。。例如，“人”，“马”和“树”作为一元关系词可以表示成形如“____是一个人”,“____是一匹马”和“____是一棵树”的形式。皮尔士从外延上来考虑关系，可以推广到四元关系，五元关系，等等。关系词的基本运算。逻辑加、逻辑乘、关系加和关系乘，等等③Peirce.Collected Papers of Charles Sanders Peirce.Vol.3.1933:p.195-209.。

皮尔士把关系词视为一种镜像(icon)的，或图像(image)的表达方式。可惜在接下来的工作中，皮尔士并没有把关系逻辑当作图式逻辑的操作对象，而是建立了代数形式的关系演算系统。究其原因，皮尔士于1880年至1885年致力于关系逻辑的研究，而他的图式逻辑(尤其是存在图)理论研究是1896年之后才开始的，所以一方面根据他对关系词的定义，另一方面根据他对存在图理论的描述，可以这样推测：如果他能够继续研究下去，关系逻辑的图式化将成为他的研究内容之一。

下面举例比较代数形式的关系逻辑命题和图式形式的关系逻辑命题。

命题“女人爱她的孩子”中有两个二元关系词，即“____是____的母亲(孩子)”和“____爱____”。做这两个关系词的逻辑乘法运算，得到“既是母子关系又是爱与被爱的关系”，其代数形式的表达式为，

(m,l)ij=(m)ij×(l)ij

这里，下标ij表示二元关系的一对变目。斜体小写字母m表示二元关系词“____是____的母亲(孩子)”或“母子”，斜体小写字母l表示二元关系词“____爱____”或“爱”。

在图式中，ij这对变目化作两条同一线(the line of identity)④在存在图系统中，同一线表示个体，相当于代数表达式中的变目。，其中一条同一线连接着“is a woman”，“loves”的施者和“is child of”的受者，而另一条同一线则连接着“is child of”的施者和“loves”的受者。

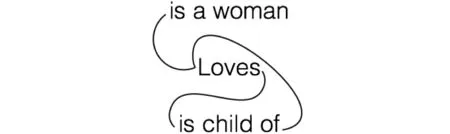
图3　二元关系命题“女人爱她的孩子”示例图

∑是存在量词，Π是全称量词。引入量词之后，命题“有的女人爱她所有的孩子”的表达式为，

∑iΠj(m)ij×(l)ij

按照由外向内的读图规则，被偶数个(包括0个)“切”，即“封闭曲线”，包围的同一线取存在量词，被奇数个封闭曲线包围的同一线取全称量词①“并非存在”可以换算为“全部并非”。。

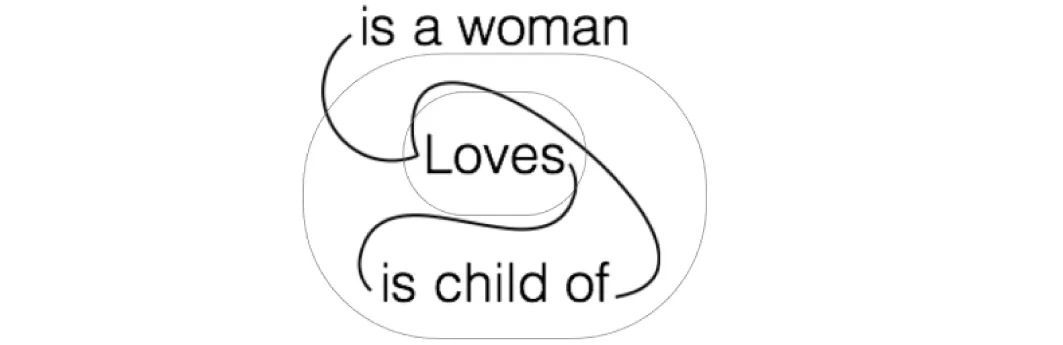
图4　加入量词的二元关系示例图

命题“一个恩人的情人”中有一个三元关系词，这三个个体分别是某人，某人的恩人，某人的恩人的情人。该三元关系词可以分解成两个二元关系，b表示“____是____的恩人”，l表示“____是____的情人”，做这两个关系词的关系乘法运算，得到“一个恩人的情人”，其表达式为

(lb)ij=∑x(l)ix(b)xj

图式的直观性体现在省略了将三元关系词拆分成两个二元关系词这一步骤，

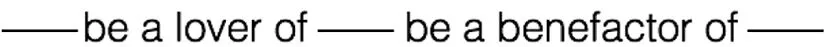
图5三元关系示例图，关系乘示例图

可见，相较于代数形式，存在图对关系逻辑的表现更为直观，而这种直观性优势在三元关系，尤其是在“关系乘”的体现中更为明显。可以推测，随着元数的增加，存在图应该能够成为表现关系逻辑命题的有力工具。

三、视知觉：范畴与颜色

在唯名论和唯实论的对立中皮尔士倾向于唯实论的立场，而在唯理论和经验论的对立中皮尔士选择了经验论的立场。由唯名论和唯实论之争说起，一方面，皮尔士赞美了经院哲学家们谨小慎微地解释亚里士多德经典的精神；另一方面，在批判了亚里士多德、康德和黑格尔的范畴理论之后，他提出了自己的范畴理论——新范畴表。皮尔士寻找新范畴目录的目的是找出适用于任何对象的更简单的，也是最简单的概念，任何其它的概念都可以化简为这三个范畴，而且其推导必须是数学意义上的。

观察(observe)、经验与新范畴表，这三者关系紧密。第一，新范畴表中的三个范畴也称为“存在的三种基本形态”，是通过观察发现到。第二，三个范畴分别为“可能性质的存在”(the being of positive qualitative possibility)，“事实的存在”(the being of actual fact)和“在将来控制事实趋势的法则的存在”(the being of law that will govern facts in the future)，简单地总结为“第一范畴：纯性质范畴”，“第二范畴：交互作用或抗争范畴”和“第三范畴：规律范畴”。第三，经验先于理性②[美]皮尔士：《现象学原理》，《皮尔斯文选》，涂纪亮、周兆平译，北京：社会科学文献出版社，2006年版，第167页。。

皮尔士多次在文章中强调观察是进行科学研究的必备技能，只有通过观察人们才能够把握事实，甚至是心灵事实，因为心灵事实也必须通过物理事实展示出来：“在任何程度上，无论心灵可被观察与否，语言学家，民族学家或历史学家，都不得不认同他的科学在很大程度上，即使不是全部，依赖物理事实。”③Peirce.Collected Papers of Charles Sanders Peirce.Vol.1.1931:p.118.而且，他认为通过科学方法能够使形而上学摆脱困境。

皮尔士在一系列讨论形而上学问题的文章中论述了这三个范畴的不可规约性，其特点如下：

表1　皮尔士的新范畴表

存在图理论是以新范畴表为基础建立起来的，反之，新范畴表依靠了存在图理论才得以直观地展现在读者面前。皮尔士运用了数学中的绘图法来推导范畴(这里体现了皮尔士的一个观点，即数学不应该以逻辑学为基础，这个观点与罗素等逻辑主义者的观点相左)。首先，在一张纸上画一个点来代表某物，即第一范畴的观念，点连成线即成为同一线。在表达某物的时候会立刻引入它者，即第二范畴观念。在两个对象之间的关系即第三范畴。没有某种关系或中介就不可能有两个对象，因此在绘图方法的推导下，即使只有一个点，实际上它已经包括了所有三个范畴。存在图之“存在”即“范畴”，“范畴”即本体。事实上，作为新毕达哥拉斯主义者，皮尔士的确是把自己的三个范畴建立在了数字1，2，3的基础上。根据皮尔士对新范畴目录的解释，任何事物都是第一范畴、第二范畴和第三范畴的综合体，存在图的任务就是把任何事物的“范畴”剥离出来。

在存在图的Gamma部分，皮尔士调动了更多的视知觉的能力，例如对色彩的知觉。颜色(Tincture)是皮尔士在研究存在图的过程中对Gamma部分做出的改进。通过颜色，皮尔士的研究范围已经延伸到了一阶模态逻辑的范畴。皮尔士运用了13种颜色，体现了他对不同的可能世界的考虑。颜色有三个世界(universe)，它们分别是金属(Metal)，彩色(Color)和毛皮(Fur)。三个世界又分成13个次世界(sub-universe)，它们分别是白色、奶油(cream)、富饶(Fer)、填充(Plomb)、深蓝色、浅蓝色、红色、绿色、紫色、灰色、棕色、黄色和橙色。这些颜色就是模态算子的图式装置，如何理解它们的意义十分关键：如果将断言页看作一张纸，那么切的一侧是这张纸的正面(recto),另一侧是这张纸的反面(verso)。金属表示正面的世界，正面世界专门负责各种必然性的情况；颜色表示反面的世界，反面世界表示各种可能性的情况；毛皮是皮尔士独创的第三世界，可以“缝”在正面和反面任意位置作为“补丁”，毛皮为了实用主义证明而被设定为“命中注定的结局”(Destined Result)，是与“肯定与否定”“必然与可能”相区别的。

下面以深色表示的“逻辑可能”(logical possibility)和浅色表示的“主观可能”(subjective possibility)为例，说明视知觉在断言页直观性方面的应用。

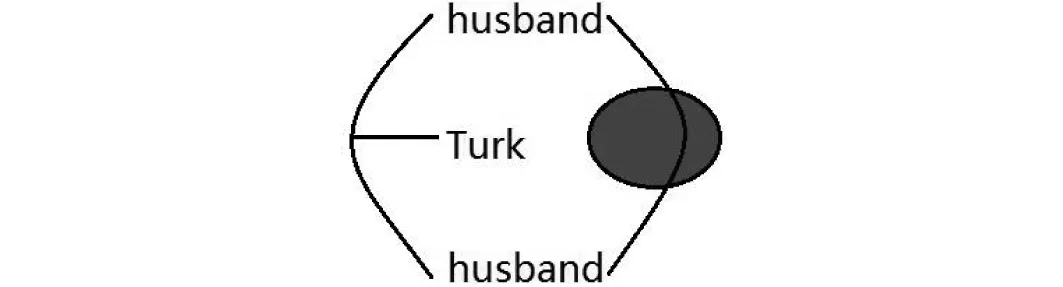
图6　命题“存在一个人，他是土耳其人，并且他是两个人的丈夫，并且这两个人并非逻辑可能地等同”的存在图

图7　命题“存在一个人，他是土耳其人，并且他是两个人的丈夫，并且这两个人并非主观可能地等同”的存在图

图8的断言是“存在两颗星，它们并非主观可能地是同一颗星，并且他们其中的一个颗是金星。”因为在天文观测水平达到一定程度之前，人们主观上不可能根据不同的时间和位置推断出晨星和暮星是同一颗星。之后随着天文观测水平的进步，相应的情况应该运用毛皮的图式装置，即“命令”(commanded)或者“强迫”(compelled)所对应的颜色。

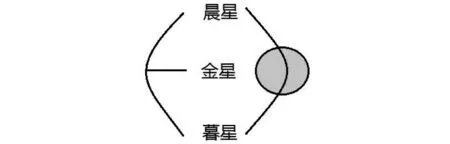
图8　命题“存在两颗星，它们并非主观可能地是同一颗星，并且他们其中的一个颗是金星”的存在图

四、结　语

皮尔士认为逻辑学是一门实证科学，逻辑学的目标是获得真理，想让形而上学摆脱困境，就必须将形而上学视作探讨经验事实的实证科学，用逻辑学来规范思想，规范形而上学的思辨。在语义学理论中，皮尔士创造出了相当于句子和命题的断言页，断言页本身就可以表达真值，从此，表达真值就不必另引入一套语义系统——“真”即为所见。在关系逻辑理论中，存在图省略了将三元关系词拆分成两个二元关系词这一步骤，由此可见，相较于代数形式，存在图对关系逻辑的表现更为直观，而这种直观性优势在多元关系，尤其是在“关系乘”中更为明显。在形而上学理论中，首先，新范畴表需要依靠存在图理论来直观地展现在读者面前。其次，当同一线穿过颜色的时候它连接了现实事物和可能事物，也就是说，它连接了现实世界和可能世界，将现实世界里的事物与可能世界里的事物连接了起来。存在图的直观性特征使它成为讨论逻辑学问题以及哲学问题的的便利工具。而且，随着对存在图理论研究的深入和补全，其在视知觉领域的扩展引起了越来越多的来自逻辑学、符号学、认知科学等领域内学者们的关注，这又说明存在图理论是一个具备活力和潜力的交叉研究领域。