自然灾害风险的一个形态发生更新算法*

田　静，黄崇福，张建毅

(1. 防灾科技学院 防灾工程系，河北 三河 065201； 2. 北京师范大学 环境演变与自然灾害教育部重点实验室，北京 100875；3.北京师范大学 地理科学学部减灾与应急管理研究院，北京 100875)

自然灾害风险是指由自然变异为主因导致的未来不利事件情景[1]，它作为自然灾害在未来发展变化的一种“投影”，显然不是静止不变的，它会随着时空的变化而呈现出差异[2]。自然灾害领域的风险分析研究已经从静态风险分析步入到了动态风险分析的初步探索阶段，动态风险问题本质上属于风险认知问题，须遵循动态风险分析的基本原理[3]来认识。目前，对动态风险分析技术的研究，主要是探讨更新算法，也就是探讨风险更新的算法问题。本质上看，风险更新属于信息更新问题，其动机和任务就是消除吸收新信息所带来的矛盾，使整个系统保持协调。其在计算机领域的发展尤为突出，在风险领域的研究成果不多。风险分析的时效性很强，使用有限的知识和资料快速进行风险计算和风险更新，是风险分析的活力所在。有关风险计算的研究相对较多，而有关风险更新的研究进展不足，需要进一步研究[4]。

探讨风险的更新问题时，首先须界定所探讨的风险的类型。黄崇福[5]认为，人们之所以对一种风险有不同的认知，原因在于我们掌握的信息不同，所以可基于人类对信息的认知水平将风险分为伪风险、概率风险、模糊风险和不确定风险四类。而概率风险由于应用较为广泛，探讨其更新模型也更具有代表性。在自然灾害风险的更新上，2008年黄崇福[6]首次提出了自然灾害风险区划图的更新原理，保真更新原则与满意更新原则，分别给出了极值区划和软风险区划的加权算法以及概率区划的加权期望值更新。2008年黄崇福探讨了模糊风险的更新问题，给出了用新观测资料直接更新由可能性-概率分布表达的模糊风险的洪水灾害分析案例[7]。2011年张俊香等[8]给出了缺失原始资料条件下台风暴雨灾害风险区划图更新案例。

因此，概率风险的更新是一个宽泛的科学问题[4]，探讨具体更新模式时，需对问题进行分解细化。具体到自然灾害领域，其存在问题为：一是有关自然灾害概率风险的更新理论尚未建立，风险更新目标、对象、方式并不统一，缺乏规范平台。二是现有更新方法需建立在大量数据基础上，但在实践中却根本不具备这样的基础。对于不确定性与复杂性较大的缺失原始资料条件下的更新问题更是少有研究成果。本文以概率风险更新问题为研究对象，提出了一类灾害风险更新的新算法——形态发生更新算法。

1　概率风险更新

1.1　基本概念

风险更新是依据最新信息对原有风险分析结果进行修正更改的过程。用概率来度量风险时，风险更新就意味着概率分布参数的变动。由图1可理解更新的目的与原因。如图1所示，总体分布为真实分布，假设它代表了某个致灾因子的概率分布。进行致灾因子风险分析时，要利用有限的观测样本去估计总体分布。从形态上看，相对于旧样本估计的总体分布，利用新旧混合样本估计的总体分布的形态与总体分布形态更为接近。这是因为由于样本的加入，提供了更多的关于总体的信息，使得对总体的估计结果更加精确了。

图1　概率分布更新示意图

从旧样本估计结果变换到新旧样本估计结果的过程就是风险更新过程。对于风险这一未来现象而言，风险更新是必然的。风险更新的目的和作用在于用最新信息修正原有认识，减少由于认识不完善造成的主观不确定性和客观不确定性。最新信息表现形式多样，涵盖了风险分析中涉及到的任何信息，例如专家经验、观测结果、社会环境变化等。最常见的风险更新是基于数据的风险更新，即最新信息为新观测资料。约束时空下的风险分析结果会随着数据量的增多或环境的改变而变化，认知并解释这一变化过程的行为就是风险更新行为。用公式可简化表达：

Updated Risk=z×Observed Risk+(1-z)×Old Risk。

(1)

式中：Updated Risk表示更新风险，Observed Risk表示由最新信息得到的风险，Old Risk指旧风险，z表示Observed Risk的权重。确定权重z是更新问题中的难点问题。

1.2　问题提出

在自然灾害风险领域，目前并无统一的风险更新理论[4]。根据给定旧风险信息的不确定性程度，可将风险更新算法分为更新Ⅰ、更新Ⅱ和更新Ⅲ三类。其中更新Ⅰ指将新的资料加入原有的资料中用原有风险模型进行更新的算法，其主要特点是旧观测资料和风险分析模型均已知，其计算结果是验证其他更新算法有效性的标准。更新Ⅱ指通过重新收集所有资料计算风险的算法，其主要特点是基于新的风险分析模型重新收集新旧资料来更新。而更新Ⅲ是缺失原始资料条件下的更新算法，缺失原始资料且旧风险分析模型不确定是它的主要特征。更新Ⅰ、更新Ⅱ相对简单，不是讨论重点，难点是更新Ⅲ，即缺失原始资料时的更新问题，这在地震危险性评估、地震动参数区划等地震工程领域常见。

同时，由于原始资料缺失，旧概率风险又通常用风险曲线或风险值来表达，故依据旧风险值的已知信息，可分为三种情况：“情况1”指已知概率分布类型与参数。例如已知原始资料得出的分析结果为期望值与方差已知的正态分布。“情况2”指不知概率分布类型，至少知道3个旧风险值的情形。例如已知特定超越概率下的取值，如概率水平为0.1，0.01等时对应的灾害参数值。“情况3”指不知概率分布类型，且仅知道1个风险值。情况3中对过去的不确定性最大，很难保证结果的可靠性。

情况1相对容易些，情况2则非常普遍。故本文以更新Ⅲ、情况2为主，解决如何从有限点(样本)获得整体结果特征，并符合保真更新与满意更新原则。

为此，本文提出了一种形态发生更新算法来解决缺失原始资料条件下概率风险的更新问题。

2　形态发生更新算法

2.1　形态发生更新原理

形态发生更新的基本思想是将新旧风险变换到以背景H表征的同一个数学空间中，通过形态计算再现旧风险和新观测资料风险的形态发生过程，以它们与背景的相似度作为加权依据。背景H提供了更新空间，将观测值与风险值联系在一起。任意风险曲线都可看作是高维对象空间中的点，作为矢量，它与背景的相似性可通过它与在背景中的投影之间的夹角余弦相似性来度量。

形态发生更新的原理如图2所示。其原理是直接从数据的形态特征出发，通过构建由过去相似形态组成的背景，建立新信息与旧风险的形态发生系统，以背景的投影算子为工具，以形态计算为技术，利用形态的记录与重现过程估计出各个形态内在结构后，再以新旧形态与背景的相似性为加权依据，计算更新风险。

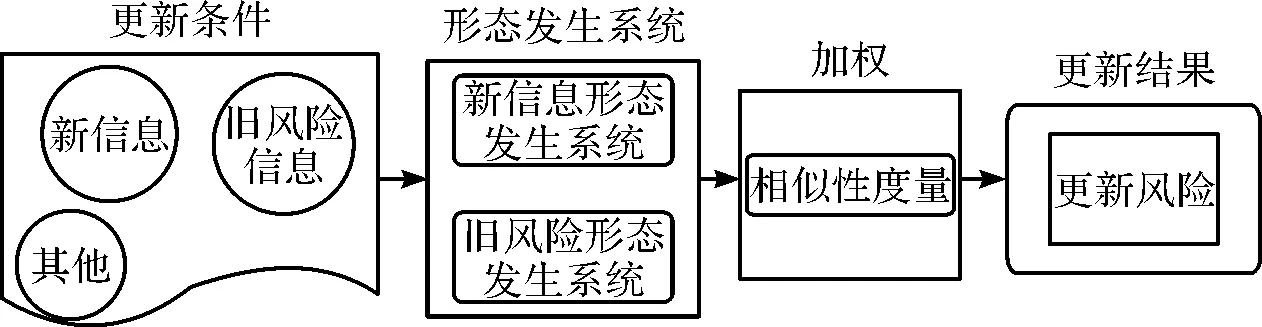
图2　形态发生更新原理

2.2　形态发生更新算法

算法分为三块，先构建背景，再由背景组建形态发生系统，由形态计算估计总体结构特征，最后利用相似性度量来加权更新。

2.2.1构建背景

背景是形态发生过程的局部环境，形态计算依赖于给定背景。以线性回归问题为例，由两条已知直线组成的线性空间即是背景。为什么要构建背景？由更新条件知，已知最新信息和旧风险值。最新信息是总体的一个样本，旧风险值是某个样本的处理结果，如何将它们变换到同一个空间呢？答案是通过形态发生系统中的背景来变换。简单地说，形态发生系统中的背景就是解决某类问题的约束环境。

图3　信息金字塔

以图3信息金字塔结构来看，最新信息属于样本值，位于最底层；旧风险信息属于样本统计量层的信息，位于中间层；总体参数为最高层，背景就是由最高层的信息组合出的代表某一形态特征的环境。在这个环境下，可观测特定形态的发生过程。最新信息与旧风险信息都被变换到背景中，这样它们就在同一个数学空间中了，在这个前提下，才可考虑加权问题。

如何构建背景呢？构建背景要从样本出发，即从最新信息出发，估计出最新信息概率值后，根据经验先构建其相似形态的背景，通过形态比较择优选择最适背景。由于假设新旧观测资料均来自同一个总体，故旧风险的背景与最新信息的背景具有一致性。背景构建时，须遵循简单原则和校正测试原则[4]。

2.2.2构建形态发生系统

更新问题需构建两个形态发生系统：最新信息的形态发生系统和旧风险信息的形态发生系统。前者描述为：以最新信息的m个观测值为对象，构成m维对象空间；以观测值对应概率值组成的矢量为输入场；以已知相似分布组成背景。由形态计算可记录和重现最新信息的形态。后者描述为：风险值由两个分量组成，即观测值与其概率，以观测值为对象，以概率值组成的矢量为输入场，以已知相似分布组成背景。由形态计算可记录和重现风险值的形态。

2.2.3加权更新

确定背景是加权的前提，它提供了同一个数学空间。如何加权呢？由于形态发生系统是一个用来记录、保存和重现所有各种形态的系统，其重现某一形态的过程其实是计算某一形态在背景中的投影。风险更新问题中，假设不同时期收集的样本服从同一总体分布，所以，当把基于给定样本得到的概率风险视为输入场时，特定背景必然是由相似分布组成的。对于同一类分布，诸如正态分布，背景不会变化。这种“不变性”便找到了处理更新问题的基准。新旧时期的风险曲线均是在同一个背景中生成的，它们与背景的相似性越大，则在加权更新中作用越大。加权更新问题转化为寻找合适的相似性度量问题。

模式相似性的定量描述主要有距离相似性度量和角度相似性度量。距离相似性度量最常用的是欧氏距离和马氏距离，角度相似性度量为夹角余弦。夹角余弦对坐标系的旋转和尺度的缩放具有不变性，受到几何学中相似形的启发，可用来衡量两个矢量方向的差异，机器学习中借用它来衡量样本矢量之间的差异。鉴于形态发生系统计算投影的特点，采用“夹角余弦相似性度量”。

在多维对象空间，任意形态均被看做是一个矢量，其投影也为矢量。假设旧风险曲线为形态A，其在背景H的投影为形态A’；新风险曲线为形态B，其在背景H的投影为形态B’。由于形态A’和B’均在背景H中，则形态A与B和背景H的差异性可通过它们与其投影的夹角余弦表达。

由于形态发生系统的对象空间一般为高维空间，所以涉及两个n维样本点a(a1,a2,…,an)和b(b1,b2,…,bn)的夹角余弦。其公式为：

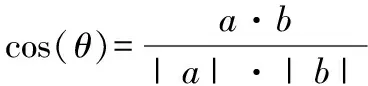
(2)

式中：θ(0≤θ≤π)表示矢量a和b夹角，|·|表示矢量的模，|a|·|b|表示矢量a和b内积。

夹角余弦取值范围为[-1,1]。夹角余弦与夹角成反比，夹角为0时，即两矢量重合时，余弦值为最大值1；夹角为90°时，即两矢量垂直时，余弦值为0；夹角为180°时，两矢量方向相反，余弦值为最小值-1。夹角余弦相似性与更新权重为正比关系，余弦值越大，则权重越大。夹角余弦值越接近于1，两者相似度越高，形态最为相近，输入场与背景的匹配程度越好。

由本文1.2知，通常的三种更新情形都可采用夹角余弦作为权重依据。

2.2.4 加权更新步骤

总的说来，形态发生更新算法为：

第1步：估计新观测资料的概率值，根据经验建立背景。

第2步：建立新观测资料的形态发生系统，计算其内源Sn和夹角余弦cos(γn)，由内源估计总体参数θn。

第3步：建立旧风险值的形态发生系统，计算其内源S0和夹角余弦cos(γ0)，由内源估计总体参数θ0。

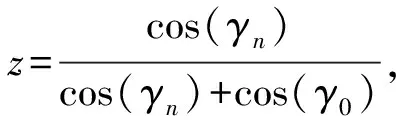
3　形态发生更新算法应用

3.1　应用实例描述

以文献[7]中提出的直方图更新问题为算例来展现形态发生更新算法的应用。

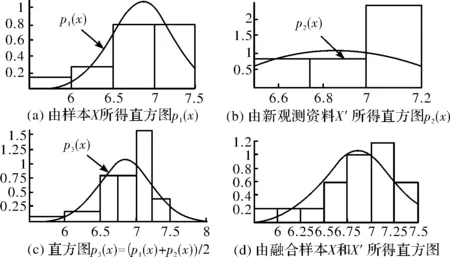
图4　缺失原始资料条件下更新问题示意图注：曲线是正态分布N(6.86,0.3722)概率密度分布的一部分

这一问题描述为：对于某个总体，抽取两个不同时期的样本，一个记为旧观测资料X，另一个记为新观测资料X′。用直方图估计方法，由X得p1(x)；由X′得p2(x)。缺失X时用加权平均方法得p3(x)=(p1(x)+p2(x))/2，它与由融合X和X′得到的更新估计有较大差异。即在缺失原始资料条件下，不能正确更新直方图p1(x)。依据风险更新条件，此类更新问题的风险分析模型为直方图估计方法，但旧观测资料未知，依据风险更新原理由于未合理地进行旧风险的反演与加权，此类更新很难实现。但用形态发生更新算法则可以实现此类更新，即在缺失X时，能正确更新直方图p1(x)。在小样本条件下，由于扩散估计结果优于非扩散估计结果，所以本文用扩散估计来替代直方图估计，所采用方法为形态发生估计的非参数估计与参数估计方法。

仿真实验设计：先设定正态总体为N(6.86,12)，使用随机数生成器先得到旧观测资料X，再得到新观测资料X′。其中

X={5.29,6.94,7.28,7.48,8.48}，n1=5。

X′={4.02,5.53,5.54,5.7,5.75,6.26,6.34,6.45,6.53,6.92,7.08,7.26,7.39,8.13}，n2=15；

算例中，旧观测资料为X，容量为5；新观测资料为X′，容量为15；新旧资料为X∪X′，容量为20。由本文1.2知，“情况2”所对应的更新问题的基本条件为：已知旧风险值与新观测资料，而旧观测资料缺失，其中旧风险值是旧观测资料的处理结果。保真更新与满意更新是评价更新模型的两个标准，这两个标准都以“由新旧资料混合后得到的风险值”这一母板为比较对象，但仿真实验中可用真实分布来验证效果。

3.2　更新过程

利用形态发生估计对三类样本(X，X′和X∪X′)分别进行估计，先利用非参数估计得到概率值，由概率值的分布形态对总体分布类别进行推断后，再建立背景利用参数估计模型得到参数值。形态发生更新算法过程如下所示。

第1步：由形态发生估计的非参数估计模型估计新观测资料X′的概率值，根据经验建立3个已知正态分布组成的背景，已知正态分布的参数由置信区间最初确定，再通过形态计算中内源取值情况进行调整。

经过非参数估计计算，给出了6个基本场函数示意图(图5)；以6个基本场为属性空间，利用场函数计算对象与各基本属性的联接程度，得到背景H(为15×6矩阵，见式(3))。

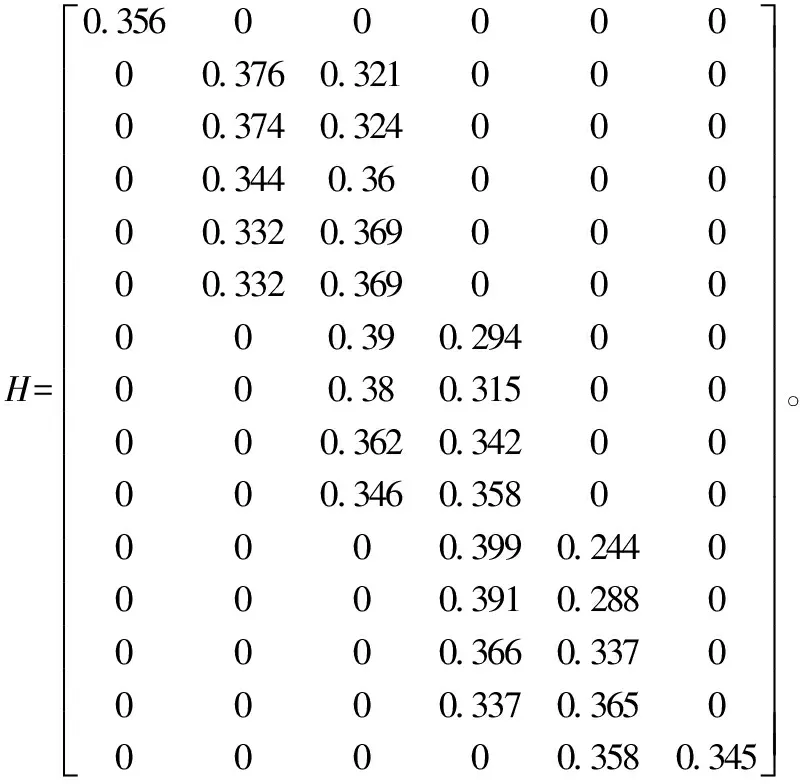
(3)

图5　6个基本场函数组成的背景

最后，由概率估计公式(4)得到新观测资料非参数估计结果——概率值估计值图6。

(4)

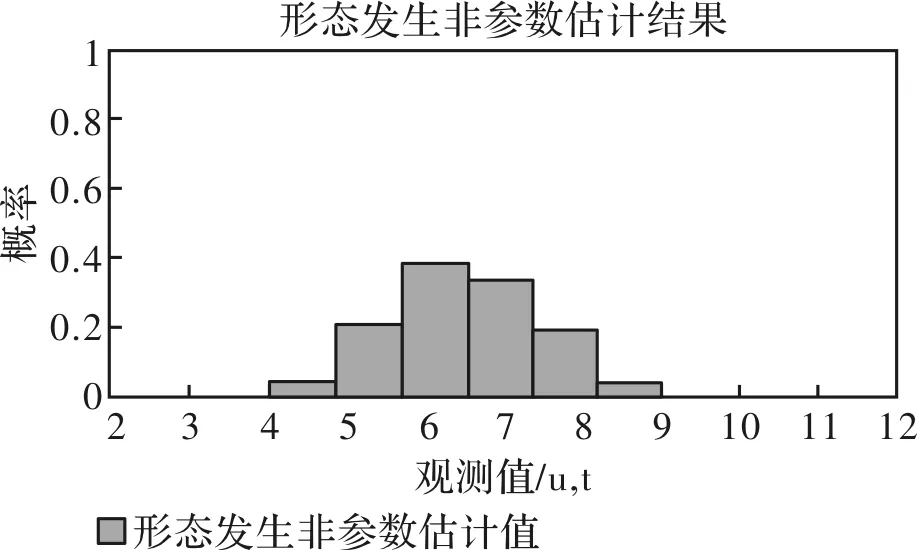
图6　新观测资料非参数估计结果

第2步：建立新观测资料的形态发生系统，对于正态分布，涉及两次形态发生系统，先由概率值的形态发生系统计算出夹角余弦cos(γn)=0.998，由形态变换后得到的直线的形态发生过程计算的内源估计总体参数θn为N(8.036,0.7942)。

其计算过程为：通过对概率值分布的形态来假设相似分布，再利用形态发生估计的参数估计模型优化。由图6的图形形态判断，总体可能服从正态分布，故建立正态分布背景来进行参数估计。背景由已知正态分布构成，已知正态分布的参数通过区间估计的置信区间来确定，再通过形态计算中内源取值来调整。样本数为15，取95%的置信水平，σ未知时，μ的置信区间为(5.762,6.865)；μ未知时，σ的置信区间为(0.729,1.57)。以四个正态分布N(5.762,0.7292)，N(5.762,1.572)，N(6.865,0.7292)，N(6.865,1.572)组成背景后，将概率值作为输入场，经过形态计算得内源为(0.43,-0.176,0.402,0.368)，由于N(5.762,1.572)的内源为负值，故删除。最终背景由3个正态分布构成。

图7展示了第1个形态发生系统的过程和结果。第1个形态发生系统为：对象为6个观测值，输入场为观测值对应概率值(图7中的6个点)；背景由3个正态分布构成(图7中的3个正态分布)。新观测资料的形态发生过程指的是图中实点(即输入场)在由个正态分布表示的背景中生成其投影(用圆圈点表示，即输出场)的过程。这一过程对应着形态计算中的写运算与读运算。写运算是计算三个正态分布对应的内源的过程，读运算是由三个正态分布与其内源叠加组合为输出场(即投影)的过程。从形态上判断，输入场与输出场相差不大，这表明所选正态分布背景能够展现出输入场的性质，故背景可接受。

图7　新观测资料概率值形态发生过程

图8所示为第2个形态发生系统，其以内源为媒介，进行形态变换，将正态分布的参数估计问题简化为线性回归问题求解。

图8　新观测资料线性形态发生过程

由图8中所得估计直线的截距与斜率来估计总体参数，得N(8.036,0.7942)，为图9中形态发生估计结果。此外，图9中还给出了真实正态分布与样本统计量结果的图形表示。

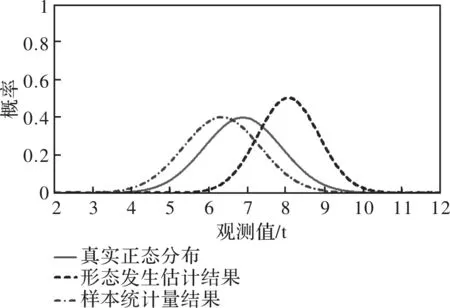
图9　新观测资料参数估计结果

第3步：同理，建立旧风险值的形态发生系统，计算其夹角余弦cos(γ0)=0.981，由内源估计总体参数θ0为N(5.855,1.3392)。对旧观测资料和混合资料进行处理的结果见图10和图11。

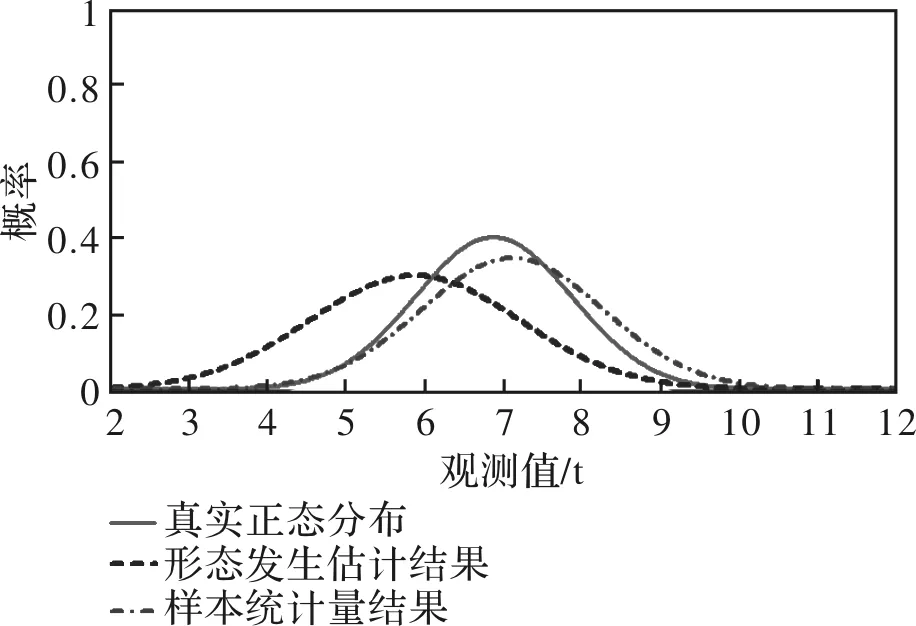
图10　旧观测资料参数估计结果

图11　混合资料参数估计结果

第4步：计算加权权重并求更新参数

3.3　计算结果分析

表1给出了各种参数估计结果，正态总体为N(6.86, 12)，将各结果与真实分布进行比较。

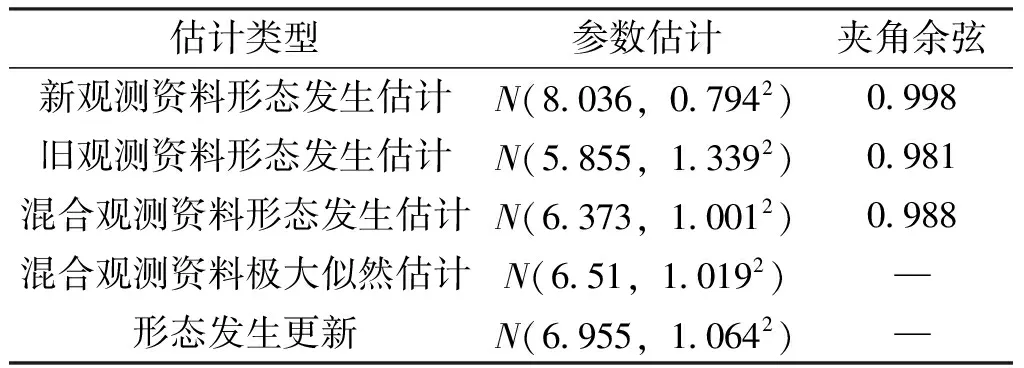
表1　参数估计结果

首先，进行形态上的比较。图12给出了形态发生更新结果与真实分布、混合资料形态发生估计结果、混合资料极大似然估计结果的对比图。由形态上看，形态发生更新结果与真实分布最为接近，两者几乎重合，所以这种更新算法是有效的；既优于混合资料极大似然估计的结果，也优于作为判断更新模型效果的母板-即由混合资料得到的估计结果。形态上看，混合资料极大似然估计的结果与混合资料形态发生估计的结果基本重合，这表示形态发生估计的效果与极大似然估计的效果相当。

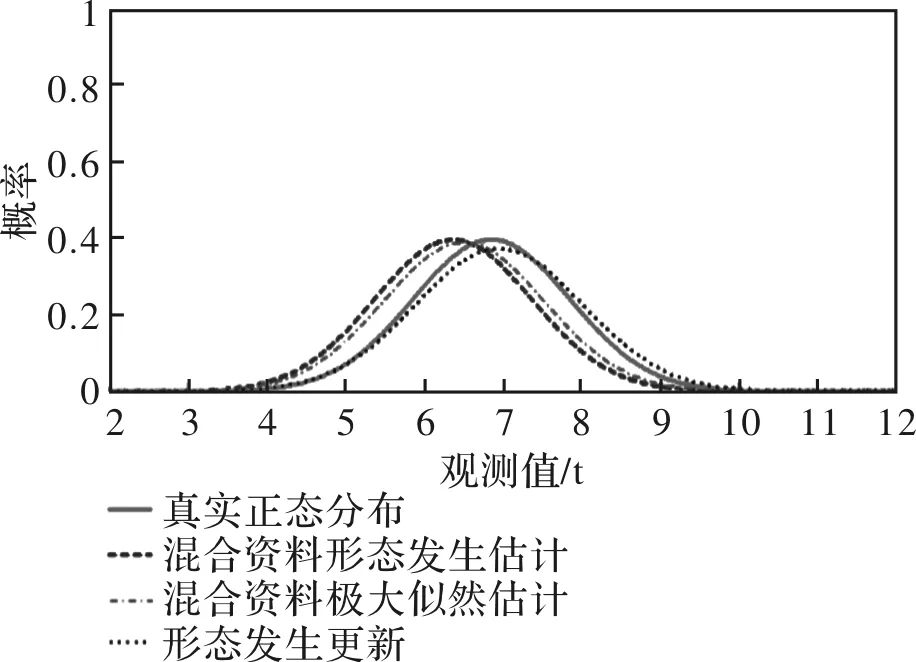
图12　形态发生更新结果对比

其次，将估计值转换为参数空间中的点进行定性比较。参数空间的横坐标为均值，纵坐标为标准差。由图13可直观地感受到形态发生更新参数值与真实分布参数最为接近，而极大似然估计参数值和形态发生估计参数值相差远一些，这表明形态发生更新算法有效。

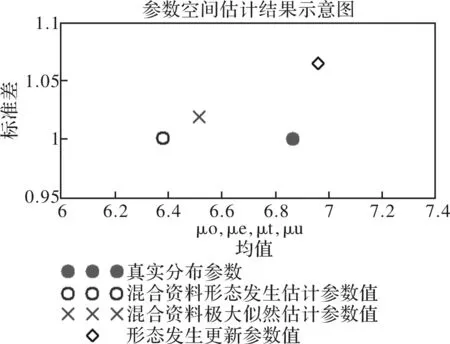
图13　更新结果参数空间示意图

最后，利用参数空间中点的距离来进行定量比较。以真实分布为基准点，通过各点到基准点的距离来度量它们与真实分布的差异。距离公式为：

(5)

式中：μ0,σ0表示基准点参数值，μ,σ表示待评价参数值。记du、dt、dm分别为形态发生更新参数值、极大似然估计参数值和形态发生估计参数值到真实分布参数值之间的距离，经计算，du=0.115,dt=0.351,dm=0.487，故du

总的来说，无论是从形态上来判断(图12)，还是通过观察参数空间中的点(图13)，或是利用点的距离进行定量判断，形态发生更新算法给出的更新结果均与真实分布最为接近，这表明形态发生更新算法有效且可行。

4　结论

开展灾害风险科学研究，需要建立完善的研究方法，其中模型与模拟技术、案例分析与实证研究是目前开展综合灾害风险研究的基本手段和技术体系之一[9]。为了给复杂、不确定性大的缺失原始资料的自然灾害概率风险更新提供具体、可行的技术，本文提出了形态发生更新原理，并给出了形态发生更新算法及其应用。

(1)剖析了灾害风险更新算法的类型，分为“更新Ⅰ，更新Ⅱ和更新Ⅲ”三大类，更新Ⅲ指缺失原始资料条件下的更新，为更新中的难点。

(2)提出了形态发生更新原理，即直接从数据的形态特征出发，通过构建由过去相似形态组成的背景，建立新信息与旧风险的形态发生系统，以背景的投影算子为工具，以形态计算为技术，利用形态的记录与重现过程估计出各个形态内在结构后，再以新旧形态与背景的相似性为加权依据，计算更新风险。同时，建立了形态发生更新算法，算法表述为先构建背景，再由背景组建形态发生系统，由形态计算估计总体结构特征，最后利用夹角余弦相似性度量来加权更新。

(3)以计算机仿真实验为工具，用算例展示了形态发生更新算法。算例表明形态发生更新的结果和形态与真实分布更接近，且形态发生更新参数值到真实分布参数值的距离要小于极大似然估计参数值到真实分布参数值的距离。

总的来说，本章从理论层面详细介绍了形态发生更新算法，并以算例详细阐述了算法应用步骤，同时论证了其有效性。

感谢减灾与应急管理研究院史培军教授课题组相关人员给出的建议与帮助。