重视教材资源 彰显文化自信

文/连州市连州中学　陈伟坚

一、背景呈现

2015年6月7日下午，在湖北省高考文科数学卷上，考题第20题是以鳖臑这一几何体为背景的立体几何问题命题。考题中出现了 “鳖臑 （biē nào）”“阳马”两个名词，涉及到了 《九章算术·商功》里的知识。

二、阳马、鳖臑

1.何为 “阳马、鳖臑”

《九章算术·商功》：“阳马居二，鳖臑居一，不易之率也”，今称为刘徽原理。刘徽注 《九章算术》关于体积问题的论述已经接触到现代体积理论的核心问题，指出四面体体积的解决是多面体体积理论的关键，而用有限分割和棋验法无法解决其体积。为了解决这个问题，他提出了一个重要原理：斜解壍堵，其一为阳马，一为鳖臑。

2.阳马、鳖臑的几何教学阐释

阳马和鳖臑是我国古代对一些特殊锥体的称谓，取一长方体，按下图斜割一分为二，得两个一模一样的三棱柱，称为堑堵。

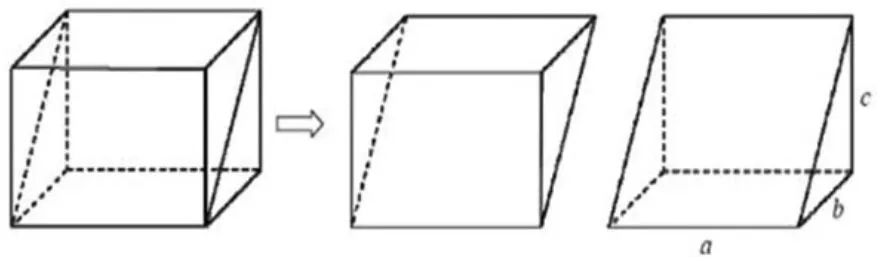
图1

再沿堑堵的一顶点与相对的棱剖开，得四棱锥和三棱锥各一个。以矩形为底，另有一棱与底面垂直的四棱锥，称为阳马。余下的三棱锥是由四个直角三角形组成的四面体，称为鳖臑。

图2

三、教材溯源，基于鳖臑的模型

人民教育出版社 《普通高中课程标准实验教科书数学必修2》中 《第二章 点、线 、面之间的位置关系》的2.3.2“平面与平面垂直的判定”里 ，教材在例题3中就给出了以鳖臑为载体的几何命题的证明问题 （第 69页）：

如图3，AB为⊙O的直径，⊙O所在平面为α，PA⊥α于A，C为⊙O上异于A，B的一点。

求证：平面PAC⊥平面PBC。

紧接着为让同学们更进一步认识这一特殊几何体，教材又借助一个探究，给同学们介绍了鳖臑几何体，并提出探究思考：

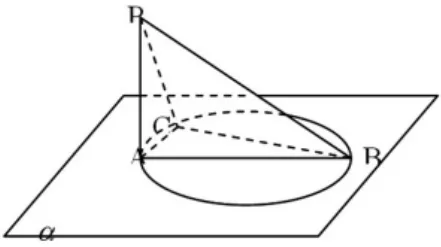
图3

如图4，已知AB⊥平面BCD，BC⊥CD,你发现哪些平面互相垂直？为什么？仔细观察，我们可以从图4中发现并证明以下现象：

1.平面ABC⊥平面BCD

2.平面ABD⊥平面BCD

3.平面ABC⊥平面ACD

4.平面ABD⊥平面ACD

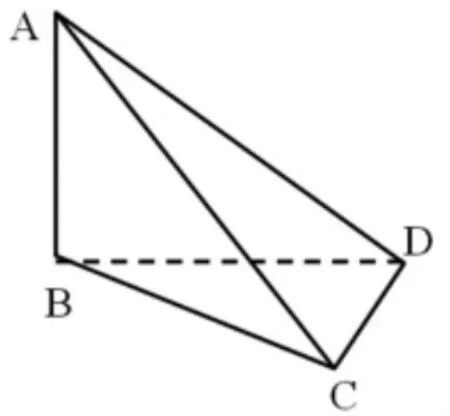
图4

该探究借助于鳖臑这一几何体中丰富的垂直关系，让学生熟悉垂直中的判定定理以及性质定理的应用。

接着在教材73页习题2.3A组第3题就设计了一道有关鳖臑的习题：

如图 5，在三棱锥 V－ABC中，∠VAB=∠VAC=∠ABC=90°，试判断平面VBA与平面VBC的位置关系，并说明理由。

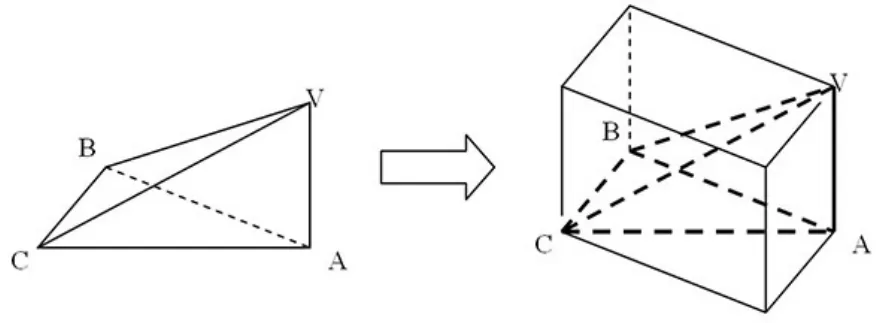
图5

由前面可知，实际上三棱锥V－ABC就是一个鳖臑，△VBC，△ABC都是直角三角形，所以BC⊥平面VBA。故平面VBA与平面VBC

教材这样的编排，遵循了学生的认知规律，有利于学生对知识理解、掌握、运用。

鳖臑几何体覆盖了立体几何中点、线、面的各种位置关系，以及各种空间角的计算，又突出了 “垂直”这个横贯立体几何知识的 “红线”，因此，鳖臑几何体是探求空间中线线、线面、面面垂直关系的十分重要的基本图形，也是研究棱锥、棱台的基本模型。

在教材中注重挖掘各种信息，并加以提高运用也是高考备考重要一个环节。我们要吃透教材，尤其是对有关中华优秀传统文化的知识，让学生真切体会中华民族的伟大，中华文化的伟大。