半空间内椭圆夹杂对出平面荷载的Green函数解

许华南, 张连刚, 汤小伟, 王永辉

(1.龙岩学院资源工程学院, 福建 龙岩　364000; 2.北京科林斯幕墙工程咨询有限公司, 北京　100020; 3.上海庞源机械租赁有限公司, 上海　200030; 4.哈尔滨工业大学土木工程学院, 黑龙江 哈尔滨　150090)

0　引言

地下复杂结构与裂纹复合缺陷对弹性波的散射解答对于爆炸力学、 地球物理学及材料力学性能的研究具有重大的工程实践意义, 在地下勘测和探索、 石油开采、 采矿工程、 地下隧道工程等领域有着广泛的应用.近20年以来, 对地下结构与复杂裂纹缺陷的解答已经有了大量的成果, 文献[1-8]采用复变函数法、 Green函数法和裂纹“切割”技术研究了孔洞、 夹杂和裂纹的散射问题； 而文献[9-13]则运用数值分析的方法、 基于边界积分方程法中的非超奇异牵引法等方法解答了孔洞、 夹杂与裂纹的相互作用问题.在已有的研究成果中, 选取的结构大都具有较为规则的几何形状边界, 而在实际工程中, 地下结构往往具有复杂的不规则的几何形状, 如椭圆形、 三角形等.研究地下不规则的椭圆形状结构对弹性波的散射问题具有重大的工程意义.

研究弹性波入射作用下地下具有复杂几何形状的结构与裂纹缺陷的动力学问题, 建立Green函数为首要问题.给定一定边界条件及初始条件, 点源入射作用下产生的位移场定义为Green函数, 本研究选取的地下结构为椭圆形夹杂, 具有不规则形状边界, Green函数不易建立.该问题模型的不规则边界可采用复变函数法中的“保角映射”方法将其映射为圆形边界, 再进一步推导弹性半空间内和表面上任意一点分别作用出平面线源载荷时产生的位移场的基本解, 即Green函数, 所得结果可为SH波入射下地下复杂结构和裂纹缺陷的动态响应问题开拓新的途径, 并进一步服务于全空间问题的解答.

1　问题描述

如图1所示为含椭圆形夹杂的弹性半空间模型, 图1(a)～(b)分别为时间谐和的出平面线源荷载作用在水平表面和半空间内任意一点的情形.介质Ⅰ和介质Ⅱ分别为基体和椭圆形夹杂, 具有不同的材料常数(ρ1,μ1;ρ2,μ2).ρi和μi(i=1, 2)分别为介质的质量密度和剪切模量.假设椭圆的半长轴和半短轴长分别为al和bl, 椭圆夹杂中心与水平地表的垂直距离为h.图中有两个坐标系：XOY和X′O′Y′, 它们之间的关系为：

x′=xy′=y-h

(1)

图1　出平面线源载荷作用在含椭圆形夹杂的弹性半空间模型Fig.1　Half-space model of elliptical inclusion impacted by an out-plane source load

2　控制方程

(2)

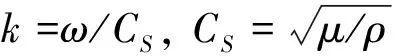
(3)

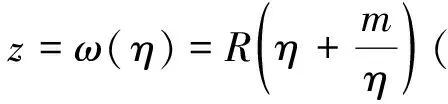
(4)

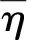
则式子(3)变成

(5)

3　弹性半空间内的位移场

在出平面线源荷载的作用下, 由于椭圆夹杂的存在会激发产生一个散射场, 夹杂内会产生一个驻波场, 具体表述如下.

3.1　基体内的散射波

在出平面线源荷载的作用下, 椭圆夹杂激发产生的散射场, 在水平表面上的应力应为零, 并满足无穷远处的Sommerfeld辐射条件, 同时还要满足控制方程(4), 则该散射场的表达式可构造为

(6)

3.2　椭圆夹杂内的驻波

(7)

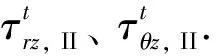
4　Green函数的导出

4.1　Green函数G1

本研究所求解的第一个Green函数为出平面荷载作用在含椭圆夹杂的半空间表面任意一点时的基本解, 用G1表示, 如图1(a)所示.

边界条件为：

(8)

在夹杂边界的法向方向, 即η=eiθ时(R=1).

(9)

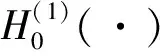
至此, 便得到了介质Ⅰ的总波场, 即第一个Green函数G1, 具体表达式如下：

(10)

总应力场为：

(11)

将相关位移场和应力场的表达式代入边界条件(8), 可推导出

(12)

其中：

用e-imθ乘以方程组(12)两边, 并在区间(-π, π)上积分, 则得

(13)

其中：

式子(13)为求解未知系数An和Bn的复系数代数方程组, 通过控制边界精度对其截断有限项进行求解.

4.2　Green函数G2

如图1(b)所示, 本研究的第二个Green函数为出平面线源荷载作用于含椭圆夹杂的弹性半空间内任意一点产生的位移场的基本解, 用G2来表示, 且满足控制方程(2).边界条件表示为式子(8).

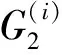
(14)

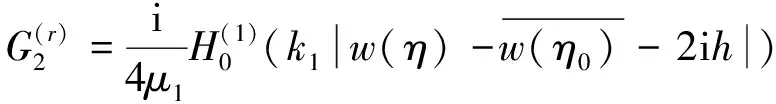
(15)

至此, 同样也得到了区域Ⅰ内的总位移场, 即本研究的第二个Green函数G2, 表达式如下：

(16)

总应力场为：

(17)

Green函数G2中未知系数的求解与4.1节一样, 不再赘述.

5　动应力集中系数(DSCF)

根据已求出的两个Green函数, 分析出平面荷载作用下弹性夹杂周边的动应力分布问题, 从而进一步验证本研究所推导出的Green函数的准确性.

(18)

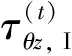
6　算例分析

选取具体算例分别得出在两个Green函数情况下弹性椭圆夹杂边缘的动应力集中系数的数据图, 分析入射波数k1, 基体与夹杂的波数比k*=k1/k2, 剪切模量比μ*=μ2/μ1, 椭圆夹杂中心到水平表面的距离h, 点源作用位置以及入射方向等参数对夹杂边缘动态响应的力学规律.动应力集中系数公式由式子(18)定义.通过验算, 当方程组(13)中m和n取7时, 边界处的计算精度达10-8, 极大满足了精度的要求, 所以本研究建立的Green函数是精确的.文献[11]基于Green函数解, 研究了弹性半空间中单个椭圆夹杂与单个裂纹的问题, 将问题模型退化为单个圆形夹杂与裂纹的情形, 并给出了同一算例下与文献[6]的数据比较结果, 通过对比得出两者的数据结果近似一致的结论, 验证了采用Green函数法解决该问题的准确性.

本研究分别考虑三种情况： 1)μ*=0.25,k*=0.5; 2)μ*=4.0,k*=2.0; 3)μ*=16.0,k*=4.0.分别表示夹杂与基体相比较硬、 较软、 更软.

1) 图2～4为出平面荷载作用在弹性半空间表面即Green函数G1情况下的数据结果.

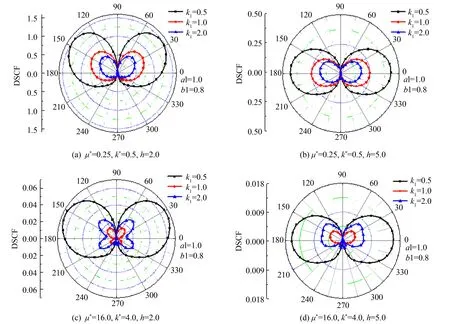
图2　DSCF随k1的变化Fig.2　Variation of DSCF with k1

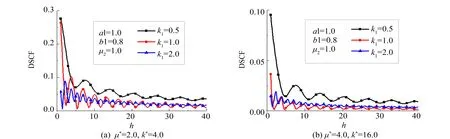
图3　θ=0°处DSCF随h的变化Fig.3　Variation of DSCF with h at θ=0°

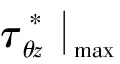
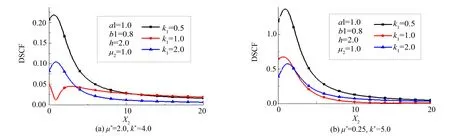
图4　θ=0°处DSCF随点源位置的变化Fig.4　Variation of DSCF with the location of the load at θ=0°

2) 图5～6给出了出平面荷载作用在半空间内即Green函数G2情况下的数据结果.

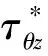
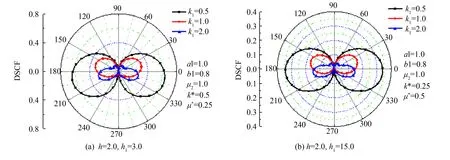
图5　DSCF的分布Fig.5　Distribution of DSCF

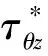
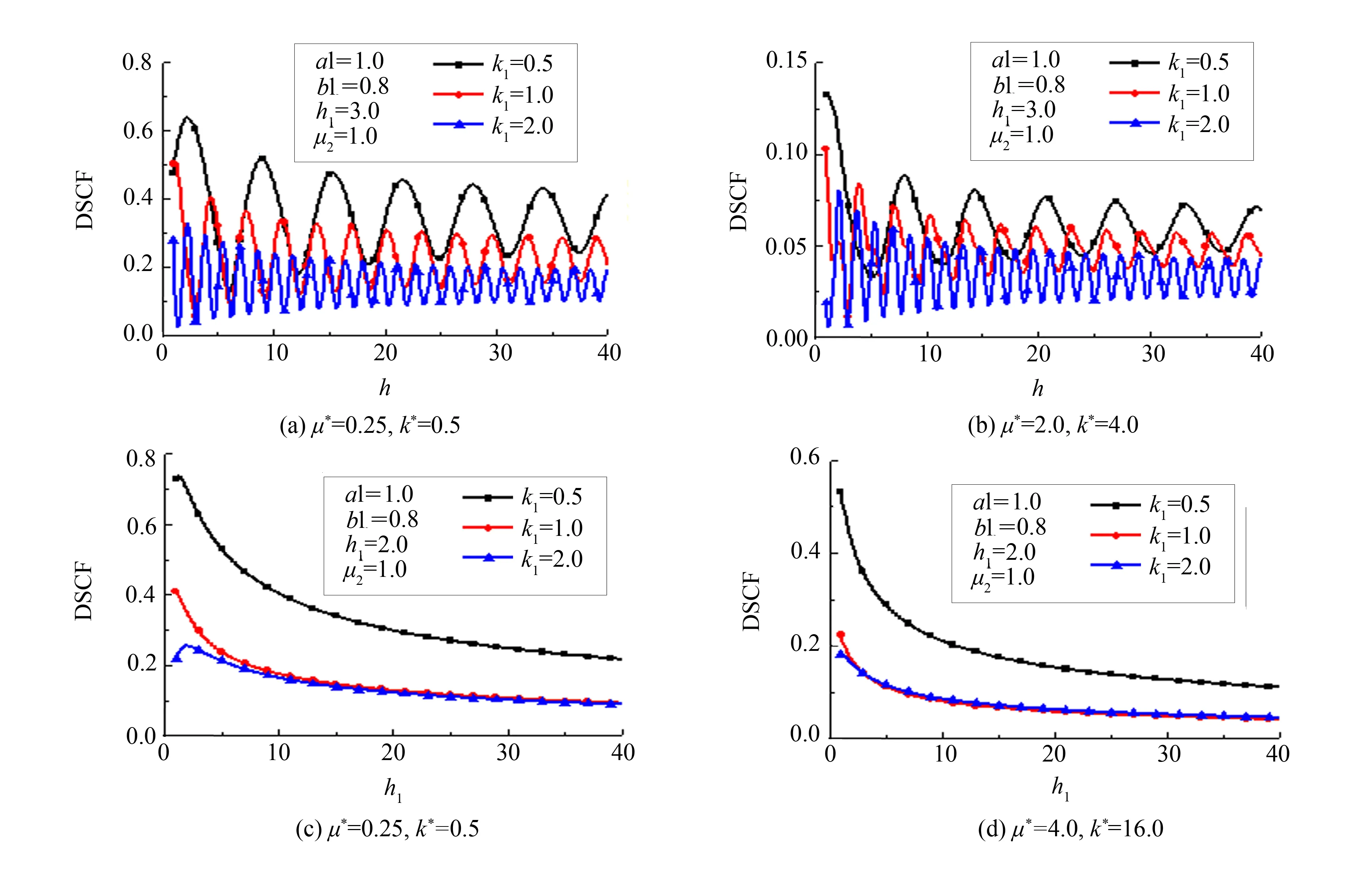
图6　θ=0°处DSCF随h、 h1的变化Fig.6　Variation of DSCF with h and h1 at θ=0°

3) 图7给出了点源荷载作用在弹性半空间内水平地表位移|G2|随入射波数k1变化的反应结果.点源荷载分两个方向(h=2.0,h1=3.0;h=15.0,h1=15.0)入射.由图7可直观地看出, 随着入射波数k1的增大, 水平地表位移|G2|的变化曲线呈现出越来越明显的振荡的动力学特征.通过图7(a)～(b)比较可知, 点源荷载作用于同一方向时, 与基体夹杂比为μ*=0.25和k*=0.5的情况相比,μ*=4.0和k*=2.0情况下的|G2|幅值要小的多.点源荷载作用位置的不同也会导致水平地标位移|G2|变化曲线的差异.图7(a)～(b)分别为点源荷载作用两个方向时|G2|的变化曲线, 通过比较发现, 点源荷载入射的位置越远, |G2|的变化曲线就越平缓, 且数值也越小.

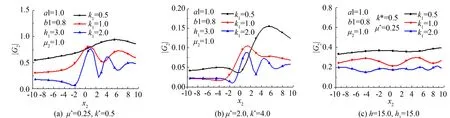
图7　地表位移|G2|随k1的变化Fig.7　Variation of|G2| with k1

7　结论

本研究选取了大量的具体算例, 给出两个Green函数情况下椭圆夹杂周边动应力集中系数、 水平地表位移的数据结果, 探讨了不同参数下弹性夹杂周边的动应力集中、 水平地表震动的力学规律, 得出以下结论.

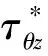
3) 本研究所得计算结果可为地下椭圆夹杂的弹性波动问题提供参考, 以所建立的Green函数为理论基础, 可进一步研究解决地下复杂结构和裂纹缺陷的动态响应问题, 拓展至全空间问题模型的研究, 为地下复杂结构的勘探、 无损检测等领域提供理论参考.