南中国海台风“莫拉菲”风场模型建立

陈 橙, 李 焱

(福州大学土木工程学院, 福建 福州　350116)

0　引言

热带气旋(如台风)是一种强烈的灾害性海洋天气系统, 危害巨大, 海面气压场和风场可直接影响到风暴潮的强度[1].强烈的台风亦可生成台风浪[2-3], 严重威胁沿海居民的生产生活.因此多年来我国学者十分重视对热带气旋的研究[4-6].南中国海海域是我国频繁遭受生成于西北太平洋和南中国海热带气旋的侵袭的地区[7-8], 故对南中国海海域的热带气旋进行研究具有典型代表性[9].

本研究建立一种南中国海热带气旋的风场模型, 选取0906号台风“莫拉菲”进行模拟, 利用实测资料进行验证, 得出风场、 气压等值线、 风速等值线等一系列数值模拟结果, 并对其进行分析, 以期对今后台风灾害的预防以及台风浪、 风暴潮的模拟起到一定帮助.

1　热带气旋风场模型

1.1　研究简介

热带气旋是一种绕中心旋转同时又向前移动的强烈气旋, 通常产生于热带洋面.国际上将底层中心附近最大平均风速32.7 m·s-1、 风力12 级以上的热带气旋定义为台风.热带气旋风场模型的研究主要有两个方向： 一是经验风场模型, 即统计模型； 二是动力理论, 即梯度风原理.国内外常见的静止圆对称风场的计算方法基本上可以分为以下两种.

第一种是用经验公式, 直接由最大风速、 最大风速半径等热带气旋要素求出风场.经验风场模型认为, 风场模型是一个可以表示台风剖面风速分布的函数表达式, 常见的有Rankine涡风场模型[10]、 Jelesnianki风场模型[11]、 Miller风场模型[12]等.Rankine涡风场模型是一个理论模型, 认为台风是一个旋转的刚体, 只能反映出台风风场的基本特征, 且计算得到的风场外围衰减较快, 使得外围风速偏小.Jelesnianki调整了Rankine涡风场模型的衰减指数, 并且提出了修正模型.Miller风场模型也对Rankine涡风场模型进行修正, 在最大风速半径内采用Rankine涡风场模型, 而在最大风速半径外改用了变化的衰减指数.

第二种是根据梯度风原理, 首先求出台风气压分布, 再由台风气压分布通过梯度风或地转风方程计算台风风场, 然后与移速进行合成.台风气压分布模型主要有3大类： 第一类是理论气压模型, 常见的圆对称气压模型主要有高桥模型、 20世纪50年代藤田模型、 Myers模型等[13]； 第二类为经验模型, 常见的有Holland模型[14]等； 第三类是半理论半经验模型, 常见的有盛立芳椭圆模型[15].这些气压模型是在理想气压条件下, 给出了以台风中心为起点的任意剖面的气压分布函数表达式, 通过这个表达式计算出整个海面的气压分布.

1.2　圆对称风场模式介绍

圆对称风场模式主要以藤田模型、 Myers模型和Holland模型为代表.

1)藤田模型：

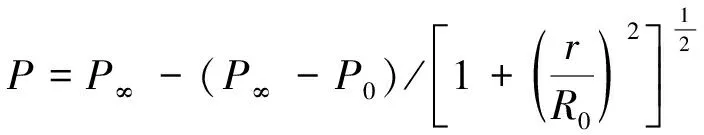
砚台里头不养鱼。卢一平从官场移身文坛,两个行业的巨大反差,让他蓦然警醒了。他发现,同官场相比,自己目前从事的,是一个投资高、回报低的行业。过去,他知道自己将成为一个富人（起码是生活宽裕的人）。那时候,他为不能成为名人心有不甘。现在,他即将成为一个名人（或者已经是准名人了）,却发现,并不能带来相应的物质回报。卢一平可以坚持下去,坚持下去,前景也很好：名气会越来越大,作品会越来越多。可是结果呢,他将成为一个有“名”的穷人！

(1)

式中：P为计算点压强；P0为台风中心气压；P∞为台风外围气压；r为计算点至台风中心的距离；R0是表征台风系统特征的参数, 可以根据最大风速半径调整, 也可以根据台站观测气压调整.

2)Myers模型：

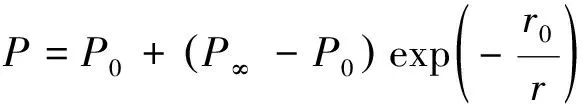
(2)

式中：P为计算点压强；P0为台风中心气压；P∞是台风外围气压；r为计算点至台风中心的距离；r0是最大风速半径.

3)Holland模型：

(3)

式中：P为计算点压强；P0为台风中心气压； ΔP为台风中心压差；r为计算点至台风中心的距离；r0是最大风速半径；B是Holland拟合参数, 取值可在0.50～2.25之间, 最优值在1.05～1.75之间.

2　模型建立

2.1　台风选取

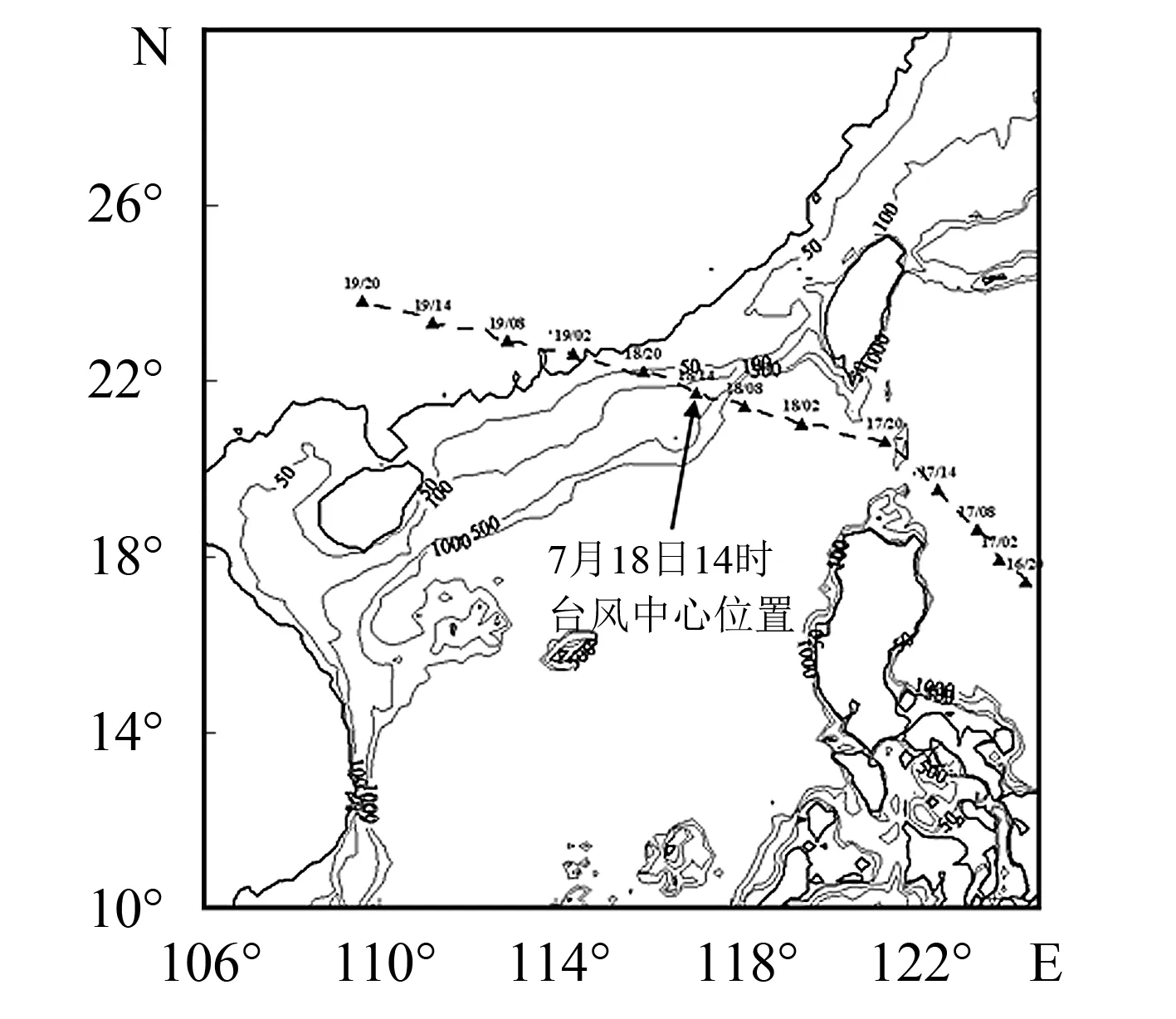
图1　台风“莫拉菲”中心的移动路径与相应时刻Fig.1　　　　Marching track of typhoon Molave and its time histories

2009年06号台风“莫拉菲”(路径图见图1)致广东省受灾人口达24万多人.台风登陆时, 惠州市沿海地区出现了10级、 阵风13级的大风和大到暴雨天气, 大亚湾马鞭洲最大风力达49 m·s-1.县(区)的37个镇(办)20万7千多人受灾, 直接经济损失近2亿元人民币.该台风发展速度快、 强度强、 危害大, 并具有如下特点： 生成于7月份, 生成源地为西北太平洋, 强度等级为台风, 移行方向为西北向, 登陆地为阳江市到深圳市一段.这些特点在建国以来的68年间登陆广东省的台风中具有非常典型的代表性, 因此研究选择该台风进行数值模拟计算.图1为“莫拉菲”移行路径, 粗实线表示海岸线, 细实线表示水深等值线(单位： m), 三角形上方标出了不同时刻台风中心所在位置(如16/20表示7月16日20时台风中心所在位置).

台风“莫拉菲”于2009年7月15日生成于北太平洋, 在菲律宾以东海域形成的热带低气压, 然后以18 km·h-1的速度朝西北偏西方向移动； 7月16号晚上升格为热带风暴； 7月17日下午14时50分升格为强烈热带风暴, 并向西北偏西移动, 速度约20 km·h-1, 移向南海北部； 7月18日上午7时40分升格为台风； 7月19号上午2点, 在深圳市盐田区一带登陆, 中心风力瞬时可达近40 m·s-1； 稍后时分, 莫拉菲以西北或西北偏西方向横过深圳一带； 上午5点, 减弱为强热带风暴, 其后稳定以西北偏西方向横过广东西部； 上午7点减弱为热带风暴, 继续向偏西北方向移动； 下午1时30分移入广西苍梧县境内； 7月19日晚上8时, 莫拉菲减弱成低压区, 逐渐消散.表1列出了台风要素.

2.2　风场计算

(4)

式中：P0为台风中心气压；P∞是台风外围气压, 取101.33 kPa；r为计算点至台风中心的距离；r0是最大风速半径, 可表示为：

(5)

式中：φ是台风中心点的纬度；vf是台风中心的移行风风速.

对式(4)求r的偏导, 可得：

(6)

梯度风的表达式为：

(7)

式中： 空气密度ρa取1.29 kg·m-3;f为科氏力参数, 可表示为f=2ωsin Ø,ω是地球自转角速度, Ø是计算点的纬度.

移行风场采用宫崎正卫公式[16], 其形式为：

(8)

式中：r为计算点至台风中心的距离；vx和vy分别是台风中心移动速度的正东分量和正北分量.vx和vy可以通过经纬度变化进行差分化求得, 表示为：

vx=111 000(θt+Δt-θt)cosφt/Δt

(9)

vy=111 000(φt+Δt-φt)/Δt

(10)

式中：θt和φt分别为t时刻台风中心的经度和纬度；θt+Δt和φt+Δt分别为t+Δt时刻台风中心的经度和纬度； Δt为两计算时刻的时间间隔.

将式(7)的梯度风表达式与式(9)、 (10)的移行风表达式进行迭加, 可得台风的风场模型表达式为：

(11)

式中：c1和c2是修正系数；α是计算点和台风中心的连线与正东方向的夹角；β是梯度风与海面风的夹角.

风场计算范围是(105°～125°E, 10°～30°N), 空间分辨率为0.5°×0.5°； 计算时间是2009年7月16日20时至2009年7月19日20时, 时间分辨率为6 h.

3　结果与讨论

3.1　结果验证与分析

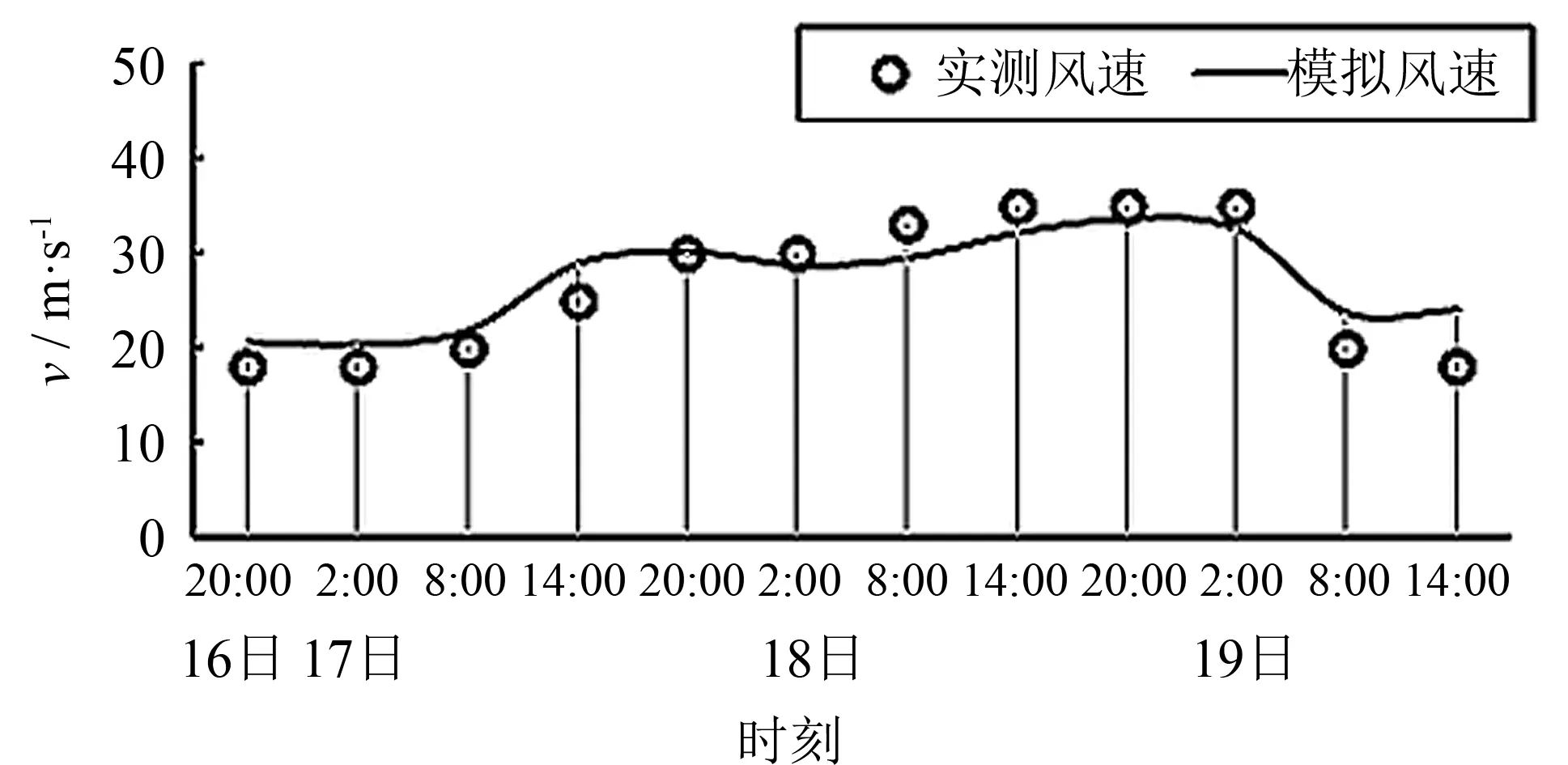
图2　台风“莫拉菲”实测风速与模拟风速最大值对比Fig.2　　　　Comparison of measured and simulated values for typhoon Molave maximum wind speed

为了验证所建立风场模型的计算准确性, 利用现实中台风实测风速的最大值来验证模型中台风模拟风速的最大值.图2为0906号台风“莫拉菲”从2009年7月16日20时至2009年7月19日14时实测风速最大值与模拟风速最大值的对比.如图2所示, 最大风速的模拟值和实测值的变化趋势相同, 且二者差值较小.其中, 该过程可分为3个时间段： ① 2009年7月16日20时至2009年7月18日02时期间, 台风中心处于远海海域(1 000 m等深线以外), 该时段的模拟风速值略大于实测风速值, 误差基本小于15%； ② 2009年7月18日02时至2009年7月19日02时期间, 台风中心经过广东沿海的近海海域(1 000 m等深线以内), 该时段的模拟风速值略小于实测风速值, 误差基本小于10%； ③ 2009年7月19日02时以后, 台风中心登陆广东省, 此后模拟风速值大于实测风速值, 误差最大值可达30%以上, 这是由于台风中心登上陆地后会受到地形以及建筑物的阻碍, 而模型中未考虑地形以及建筑物摩阻的影响, 这是今后有待于改进的方向之一.

3.2　台风风场

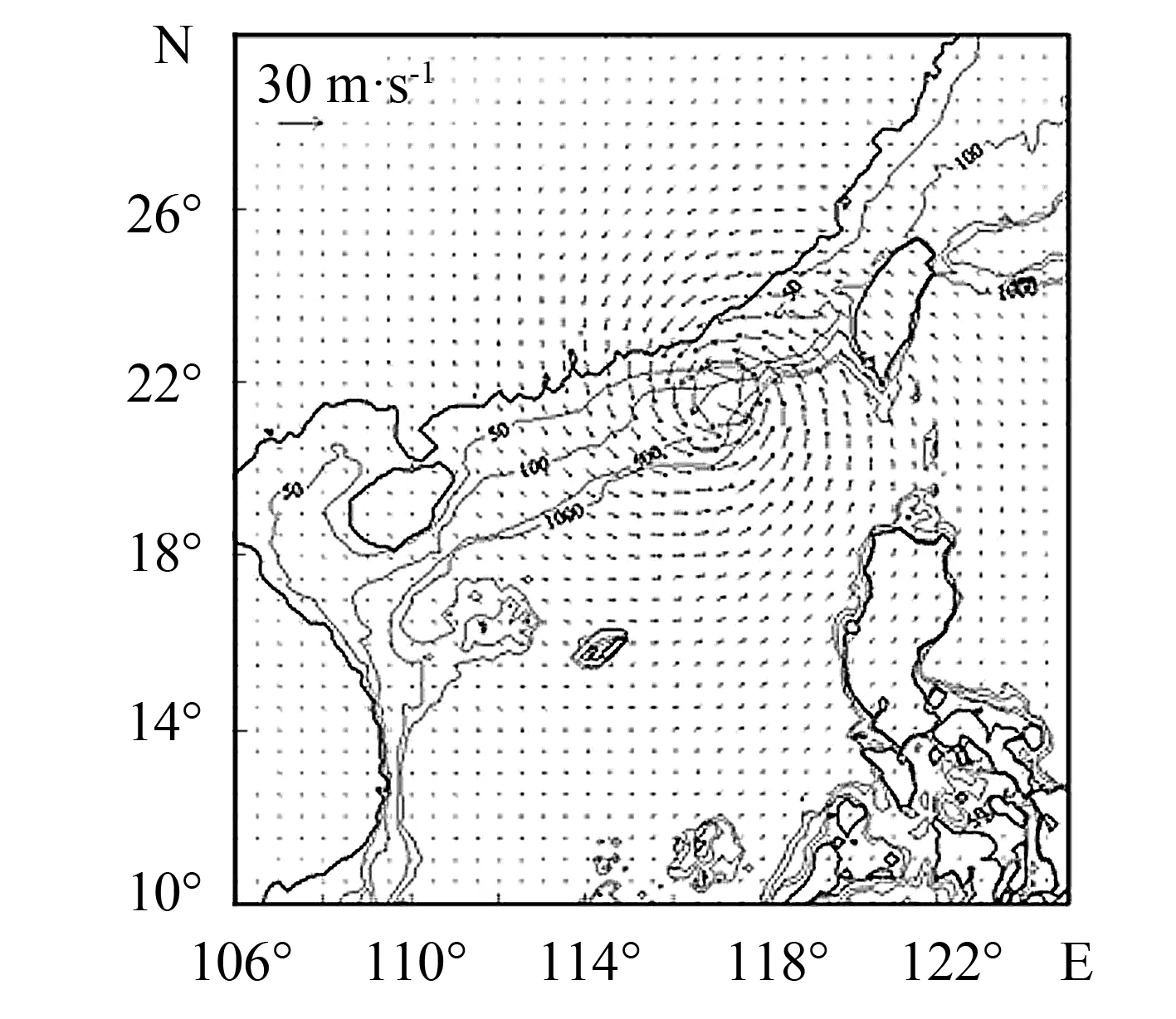
图3　模型计算出的台风风场(2009年7月18日14时)Fig.3　　　　Simulated wind field from model results (14:00 July 18th, 2009)

台风风场是台风特征最直观的体现.图3为模型计算出的2009年7月18日14时台风风场, 该时刻台风中心位于1 000 m与50 m等深线之间.由计算结果可知, 在台风影响下, 台风中心附近的风场大致沿着台风中心呈现圆对称分布, 各计算点的风向均指向逆时针的方向, 这亦符合北半球热带气旋的实际特征.由于北半球地转偏向力指向运动方向右侧, 与气压梯度力合成后, 气团由外围流向中心便形成逆时针的运动方向.最大风速处于台风中心附近, 可达32.2 m·s-1, 风速大小沿着台风中心向外围递减.此外, 台风的影响一般仅限于直径几百公里范围内, 台风外围风速强度较小.由此可推测, 在台风中心附近海域形成的台风浪亦呈现逆时针旋转的方向, 该风场有助于计算台风中心附近的浪高与波向.

3.3　风速等值线

风速等值线亦是台风的重要特征之一, 它直接反映台风灾害的破坏强度.图4是模型计算出的2009年7月18日14时的台风风速等值线.由计算结果可知, 在台风中心附近, 风速等值线的分布和气压等值线的分布趋势相似, 二者密切相关.在台风中心, 风速可高达32 m·s-1以上, 而在台风的外围, 风速逐渐减弱至4 m·s-1.值得注意的是, 风速等值线的计算结果虽与气压等值线相关, 但并不是严格服从圆对称分布, 而是呈现出不对称的椭圆形, 这一现象在台风中心附近尤为明显； 在台风行进路线的左侧(西南侧), 风速等值线略微向里凹, 在台风行进路线的右侧(东北侧), 风速等值线略微向外凸, 这说明台风行进路线的左侧风速较小, 而行进路线的右侧风速较大.这一现象的原因是因为在Myers模型中加入了宫崎正卫模型的移行风速的影响, 即Myers模型中的风场绕台风中心逆时针旋转, 而宫崎正卫模型的风场沿着台风行进的方向, 当两个模型叠加时, 台风行进路线左侧的风速减弱, 台风行进方向右侧的风速加强, 这就形成了“左小右大”的风场现象.

3.4　气压等值线

气压等值线反映了台风影响下的气压分布特征.图5是模型计算出的2009年7月18日14时的台风气压等值线.由计算结果可知, 气压等值线围绕着台风中心基本服从圆对称分布, 这与Myers模型的设想一致.气压呈现出“中心低, 外围高”的变化趋势, 越接近台风中心, 气压等值线的变化梯度越大.由图5可知, 99.9 kPa的气压等值线范围大致对应着20 m·s-1的台风风速区域.在台风中心, 气压可低至97.0 kPa； 而在台风的外围, 气压逐渐恢复至标准大气压101.1 kPa, 即不受台风的影响(此时台风风速已降至4 m·s-1之下).

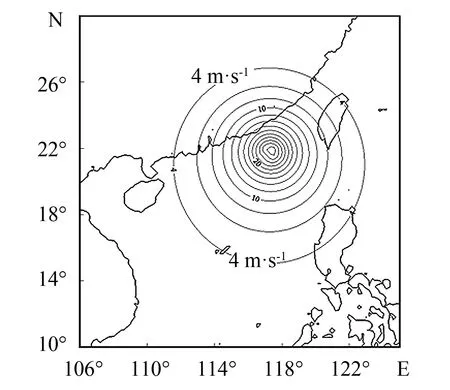
图4　　　　模型计算出的台风风速等值线(2009年7月18日14时)Fig.4　　　　Simulated wind speed contour from model results (14:00 July 18th, 2009)

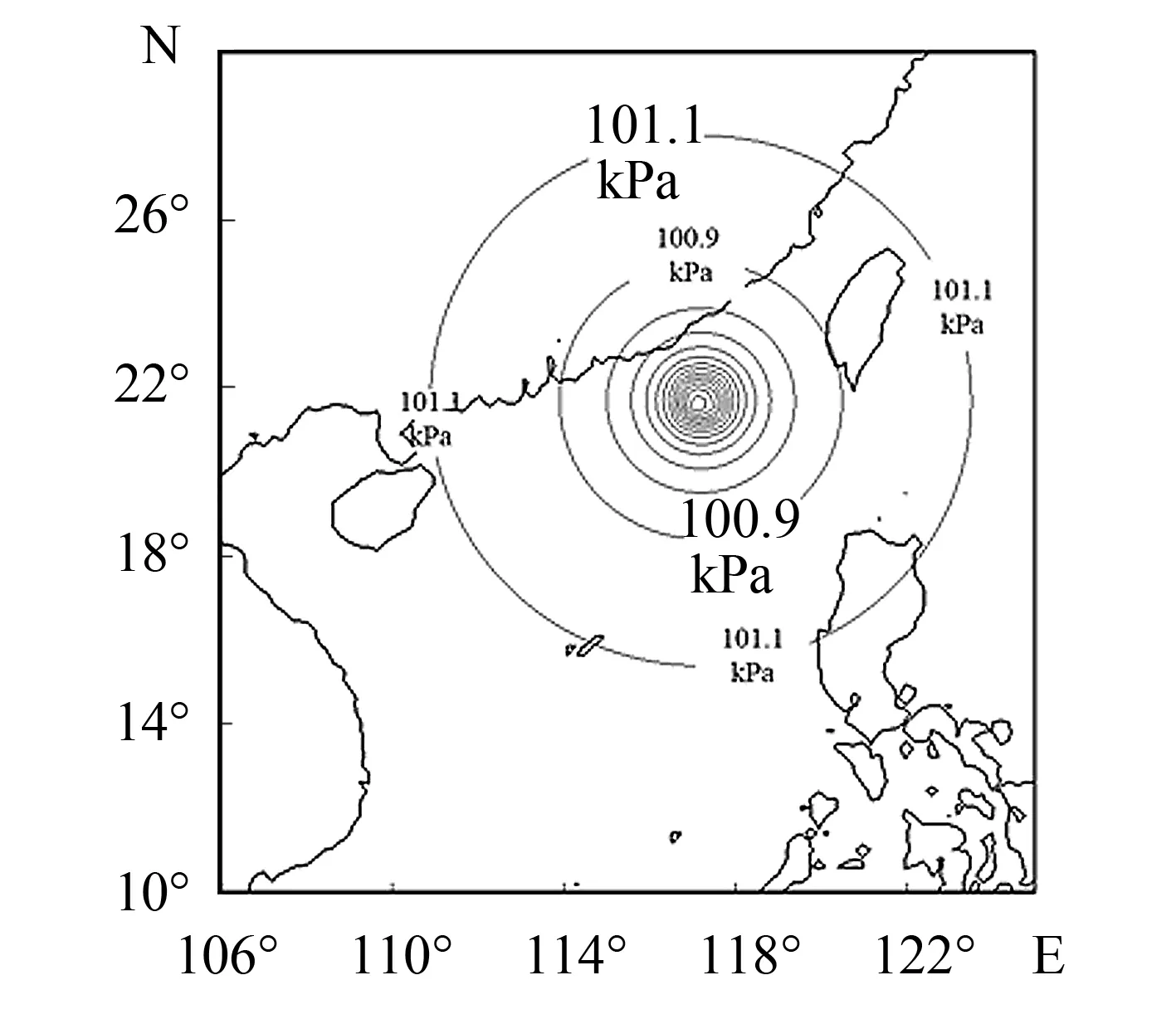
图5　　　　模型计算出的台风气压等值线(2009年7月18日14时)Fig.5　　　　Simulated barometric isoline from model results (14:00 July 18th, 2009)

4　结语

对热带气旋的风场模型进行介绍, 包括研究进展以及主流的圆对称风场模式.选取2009年06号台风“莫拉菲”的特征要素, 利用Myers圆对称风场模型, 与宫崎正卫的行风场相结合, 建立了热带气旋模型, 结果表明该模型在台风中心登陆陆地前具有较好的计算精度, 可用于推测台风浪的高度和方向.计算结果表明, 台风风场、 气压等值线、 风速等值线均围绕台风中心呈现圆对称分布, 符合实际情况.由于移行风的影响, 在台风行进方向形成了“左小右大”的风场现象.模型未考虑陆地上的地形及建筑物的摩阻, 造成了台风登陆陆地后模拟结果偏大的情况, 这是今后需要改进的方向之一.