基于双地震动强度指标的桥墩地震易损性模型研究

陈力波, 王化河, 黄才贵, 涂 意, 谷 音

(福州大学土木工程学院, 福建 福州　350116)

0　引言

桥墩作为桥梁的主要构件, 在以往地震中往往发生较为严重的破坏, 因此对桥墩的抗震性能的评估具有重要意义.地震易损性分析作为地震风险评估中的一个重要环节, 可以从概率层面对桥梁的抗震性能进行有效的评估, 近年来不同学者对地震易损性问题展开了相关的研究, 其中地震动强度指标(intensity measures, IM)的选择尤为关键.Apostolopoulos等[1]在桥梁地震易损性的研究中, 选择地表峰值加速度(PGA)为地震动强度指标, 分析得到桥梁易损性模型.Goda等[2]对非延性框架结构进行倒塌易损性分析, 选取谱加速度(Sa(T))为地震动强度指标构建倒塌易损性模型.陈力波[3]针对汶川地区典型简支梁桥构建了桥梁概率性地震需求模型, 对地震动强度指标进行刷选.

基于单一地震动强度指标建构的易损性模型, 在预测结构的损伤概率时存在一定偏差.Rajeev等[4]基于两个不同周期的谱加速度对框架结构进行风险评估, 结果表明, 与单一地震动强度指标相比, 双地震动指标提高了地震风险评估的准确性.李宁等[5]通过双地震动强度指标的易损性曲面对桥墩的损伤概率进行分析, 结果表明双指标地震易损性曲面可以更准确地评估桥墩的抗震性能.虽然部分学者对双地震动强度进行了初步研究[4-6], 然而这些研究依然存在部分欠缺.

本研究选取工程实际中较为常用的21种地震动强度指标, 采用受试者工作特性分析方法(receiver operating characteristic, ROC)对其进行评价, 选择出有效性较好的地震动强度指标, 同时基于线性组合的方法分别建立双地震动强度指标和单地震动指标的桥墩易损性模型, 通过对比更加合理地评估桥墩的地震风险, 研究结果可为桥梁结构的后续风险评估及加固决策提供参考.

1　桥墩地震易损性模型理论

1.1　基于IDA的地震易损性模型

桥墩地震易损性模型具体可以表述为： 在某一地震动作用下, 桥墩达到某种损伤状态的超越概率.本文假设桥墩的地震易损性函数为对数正态分布[1-2]形式, 具体表达式如下：

(1)

式中：C为桥墩抗震能力;D为桥墩的最大需求;X为所选用的地震动强度指标IM;m和β分别为易损性模型的中位值和对数标准差.

IDA方法最早由Bertero提出[7], 经由Vamvatsikos和Cornell等的发展[8], 在结构的地震易损性分析中应用广泛.基于IDA方法开展桥梁结构的地震易损性分析, 具体流程如下： 首先选择一系列地震动记录, 按PGA进行调幅缩放, 利用SeismoSoft软件得到所调幅缩放后的地震动强度指标, 然后对桥墩进行非线性时程分析, 得到桥墩地震响应； 选择桥墩的损伤指标并定义其极限状态值, 然后对桥墩进行ROC分析, 获得有效性较好的IM, 同时对筛选出的IM进行组合后再次进行ROC分析, 选择出组合效果较好的IM, 通过线性组合方法建立桥墩地震易损性模型.

1.2　墩柱极限状态定义

参考美国FEMA灾害评估手册HAZUS[9], 将桥墩的损伤状态分为5个性能水准.位移延性系数作为常用的桥墩损伤指标, 既能反应墩柱的变形能力也能体现其承载能力, 参考Hwang提出的5级抗震性能水准进行划分[10].从既往研究中发现, 近断层地震动作用下墩柱顶部残余位移是刻画结构或者构件损伤的重要参数[11], 通过查阅文献[12-13]确定得到5级抗震性能水准划分.位移延性系数μΔ与残余位移漂移率DR具体如表1所示.

表1　位移延性极限状态

2　桥墩样本设计及非线性动力时程分析

2.1　桥墩样本设计及有限元建模

研究中充分考虑了桥墩参数的随机性, 其中桥墩直径、 长细比(剪跨比)、 轴压比、 配筋率、 配箍率采用3水平刻画, 混凝土强度、 纵筋强度、 箍筋强度采用2水平刻画.根据文献资料以及调研结果[14-15], 现将桥墩各个设计参数的取值汇总如表2所示.由于桥墩分析参数所取的水平数不同, 采用混合水平正交设计方法进行分析, 最终确定的混合水平正交设计试验表为L36(23×35), 共计36个桥墩样本.

基于OpenSees[16]平台建立桥墩有限元模型, 桥墩采用非线性纤维单元模拟.选择Concrete01WithSITC Material来模拟约束和非约束混凝土材料[17], 基于Lee的建议, 重复加载应变的值取为0.02[18]； 钢筋本构模型选用的是Giuffre-Menegotto-Pinto本构模型.桥墩的阻尼选用Rayleigh阻尼模式, 其中阻尼比为3%.本文未考虑桩土效应对桥墩地震响应的影响, 墩底直接采用固接模拟.

表2　墩柱分析参数及其取值

2.2　桥墩非线性动力时程分析

1) 地震动输入.美国太平洋地震研究中心数据库提供了近40年来全球范围内具有代表性的地震动有关数据.通过查阅相关文献制定的筛选条件如下： 震级为6～8； 断层距为0～100 km； PGV/PGA在0.15附近.其中: 断层距为0～20 km、 PGV/PGA>0.15为近断层地震动; 断层距为20～100 km、 PGV/PGA<0.15为远场地震动.基于上述条件, 共筛选出60条地震动, 其中包含30条近断层地震动、 30条远场地震动.为了更加真实和有效地反映桥墩的地震响应, 本文采用三向地震波输入方式和地震动截断处理[19].

2) 地震动强度指标分类和选择.地震动强度指标一般可以分为3种类型： 峰值型强度指标、 频谱型强度指标和综合型强度指标[3].选用地表峰值加速度PGA、 地表峰值速度PGV、 地表峰值位移PGD、 持续最大加速度SMA、 持续最大速度SMV、 Arias强度IA、 加速度谱强度ASI、 均方根加速度Arms、 均方根速度Vrms、 均方根位移Drms、 特征强度Ic、 地震动峰值的比值PGA/PGV和不同周期对应的频谱型地震动强度指标Sa, 共计21个地震动强度指标进行后续分析计算, 汇总见表3.

表3　地震动强度指标汇总

3　受试者工作特性分析

受试者工作特性(ROC)分析是一种数理统计方法, 通常根据一系列不同的二分类方式, 以真阳性率(灵敏性)为纵坐标, 假阳性率(特异性)为横坐标绘制曲线, 从而反应体系的敏感性与特异性关系.该方法是国际公认的比较、 评价参数效能差异性的客观标准方法, 被广泛应用于气象学、 医学诊断等领域[20].在进行ROC分析时, 首先将评估的目标分为理论组与检验组, 而且两组的数目保持一致； 然后确定理论组的阈值, 若理论组的数值大于阈值记为1, 反之记为-1; 再统计检验组实际检验的状态, 同样将符合条件的记为1, 不符合条件的记为-1, 根据这两组结果便得到一个混淆矩阵, 见表4.

表4　ROC混淆矩阵

其中TP、 FP、 FN、 TN分别代表真阳性、 假阳性、 假阴性、 真阴性的统计个数.通过统计所有混淆矩阵中的状态可以得到敏感性参数、 特异性参数、 准确性参数.其中, 敏感性用真阳率(TPR)来表示, 特异性用假阴率(FPR)来表示, 准确性用ACC来表示, 其计算公式具体如下:

(2)

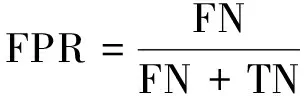
(3)

(4)

表5　ROC评价指标(AUC)

研究学者一般是通过面积指标(AUC)、 准确率指标以及敏感性、 特异性指标对评价参数进行判断.其中, AUC可直接反应参数效能的好坏, 因此面积指标应用最为广泛.根据式(2)～(4), 计算得到真阳率(TPR)、 假阴率(FPR)与准确率(ACC), 将每个点(假阴率, 真阳率)依次绘于坐标中, 并用光滑的线进行连接, 便可得到桥墩的ROC曲线.利用梯形公式计算ROC曲线下的面积(AUC), 如下式.依此进行评价, 目前公认的AUC区分标准见表5.

(5)

式中：N为阈值的数目；x代表假阴率；y代表真阳率.

3.1　基于单IM桥墩ROC分析

对前述选择的60条地震动进行分组, 编号1～30为理论组, 31～60为检验组.桥墩的损伤概率阈值P0, 其范围是[0, 1].在程序调试过程中发现： 当阈值的个数为150时, 真阳率与假阴率基本满布[0, 1], 从而保证计算结果的可靠性.考虑桥墩的两个损伤指标, 根据桥墩的地震响应结果, 基于多样条分析思想的估计方法[21]得到桥墩易损性模型及其参数, 得到损伤混淆矩阵.根据公式(5)计算出AUC值, 参考表5对地震动强度指标进行评价.由于地震动强度指标众多, 本文仅列出每种强度指标综合排列的前4个, 具体结果见表6.

表6　地震动强度指标评价结果

3.2　基于双IM桥墩ROC分析

上一节中已对单IM进行了ROC分析, 并对IM的有效性进行了判断.进一步将对筛选出的IM进行组合, 具体选择的地震动强度指标有： PGA、 PGV、 Arms、 Vrms、IC、 ASI、Sa(T=0.4 s)、Sa(T=1.0 s)、Sa(T=2.0 s)、 PGV/PGA, 共组合出33组IM, 并建立两个IM的地震易损性曲面.本文假定地震易损性函数服从对数正态分布, 如式 (1)所示, 其中地震动强度指标X根据既往学者的研究, 采用线性相加的形式组成[22], 如下式：

(6)

式中：α1,α2为两个地震动强度指标线性组合的回归系数.

将式(6)代入式(1), 得到同时考虑两个地震动强度指标的易损性函数表达式, 如下式：

P[D≥C|IM1, IM2]=Φ[β1ln(M1)+…+β2ln(IM2)-β0]

(7)

式中：β1=α1/[(α1+α2)×β],β2=α2/[(α1+α2)×β],β0=ln(m)/β为易损性模型中的参数.

本文采用广义线性回归模型中的Probit模型对3个参数进行估计[23], 通过以上分析步骤建立桥墩基于双IM的地震易损性模型, 同时根据3.1节进行ROC分析的步骤, 进一步对双IM组合进行分析比较.本节中共分析了33组双IM, 经过对比统计发现有两组IM的计算结果较为理想, 具体如表7所示.比较ROC评价指标发现： 同时考虑两个地震动强度指标其有效性与单一地震动强度指标相比有较大的提高, 其中以PGV与PGV/PGA组合的效果最好.

表7　ROC分析结果

注： 由于PGV/PGA是非常规地震动强度指标, 具有随机性, 其计算出的AUC为0.5, 没有采用其进行易损性分析

4　基于双IM桥墩地震易损性模型研究

4.1　桥墩地震易损性曲面模型

根据3.2节中的分析结果, 本节分别针对PGV与PGV/PGA、Sa(T=0.4 s)与Sa(T=2.0 s)两组IM组合来进行地震易损性分析.其中, 第一组地震动强度指标组合不存在相关性, 第二组组合存在较强的相关性.根据桥墩在地震作用下的响应, 同时考虑位移延性系数与残余位移漂移率, 采用广义线性回归方法得到桥墩每一损伤状态的参数及其概率, 进而得到桥墩基于双IM的易损性曲面, 具体结果如图1、 图2所示.由图1可知: 随着地震动强度增加, 桥墩除了完全损伤时概率增幅较小外, 其它各类损伤增幅较大.其中, 当固定PGV/PGA时, 随着PGV的增加, 4种损伤状态概率增加的幅度随着损伤等级的提高而逐渐减小, 当PGV取值固定时, 随着PGV/PGA的增加, 桥墩发生4种损伤的概率逐渐增加, 但增加幅度较小.可见PGV对桥墩损伤概率的影响要大于PGV/PGA的作用.

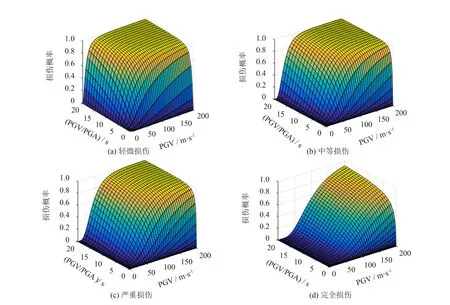
图1　桥墩的地震易损性曲面(PGV、 PGV/PGA)Fig.1　Seismic fragility surface of piers(PGV、 PGV/PGA)

由图2可知： 随着Sa(T=0.4 s)与Sa(T=2.0 s)的增加, 桥墩发生损伤概率逐渐增加.在桥墩发生轻微损伤时, 由其易损性曲面可以看出两个坐标轴的曲面缓陡情况有较大不同, 说明在轻微损伤时Sa(T=0.4 s)的作用要高于Sa(T=2.0 s).桥墩在其余的3种损伤状态, 曲面两侧的缓陡情况基本相近, 说明两者对桥墩损伤的影响相近.

图2　桥墩的地震易损性曲面(Sa(T=0.4 s)、 Sa(T=2.0 s))Fig.2　Seismic fragility surface of piers(Sa(T=0.4 s)、 Sa(T=2.0 s))

4.2　桥墩地震易损性模型对比

为更好地研究基于双IM的地震易损性曲面模型, 对地震易损性曲面模型与单IM地震易损性曲线模型对比分析,固定PGV/PGA, PGV由小到大变化结果如图3所示.

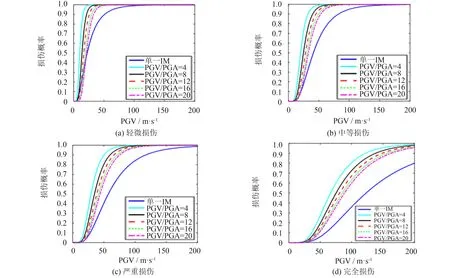
图3　桥墩易损性模型对比(PGV/PGA)Fig.3　Seismic fragility models’ comparison of piers(PGV/PGA)

通过对比图3可以发现： 双IM得到的4种损伤状态的中位值有大幅度的减小, 但随着PGV/PGA的增大, 两种模型得到的中位值偏差逐渐减小, 对数标准差也有相应的减小, 说明双IM的易损性曲面模型预测桥墩的损伤概率较大, 而且其离散性较小, 可以更好地预测桥墩发生的损伤.

第二组为Sa(T=0.4 s)与Sa(T=2.0 s), 两者存在较强的相关性[22].当其中一个IM取值较小时, 另外一个IM取值不可能过大, 即两个地震动强度指标的数据点仅在一定区域分布.因此, 本文将在对数空间里对其进行线性拟合, 确定出两者数据点的分布范围, 并根据其预测值95%置信区间来确定取值范围.Sa(T=0.4 s)与Sa(T=2.0 s)在对数坐标系中的拟合关系如下所示：

ln[Sa(T=2.0 s)]=1.010×ln[Sa(T=0.4 s)]-1.262

(8)

对应的预测值95%置信区间的上下限分别为：

ln[Sa(T=2.0 s)]=1.010×ln[Sa(T=0.4 s)]-1.262±1.202

(9)

根据公式(8)、 (9)可得到Sa(T=0.4 s)与Sa(T=2.0 s) 及其预测值95%置信区间的线性拟合关系.根据拟合结果可确定地震动强度指标范围, 根据拟合关系式得到易损性曲线模型, 如图4所示.

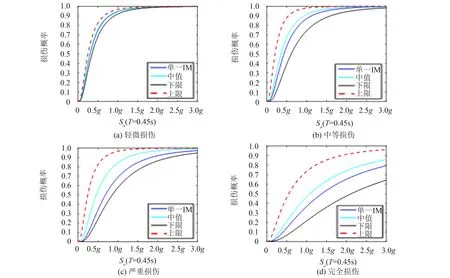
图4　桥墩易损性模型对比(Sa)Fig.4　Seismic fragility models’ comparison of piers(Sa)

由图4可以看出： 桥墩基于单一IM所得到的4种损伤状态易损性模型的中位值均小于基于双IM线性拟合所得到的易损性模型的中位值, 说明桥墩基于双IM发生4种损伤的概率比基于单一IM所发生的损伤概率要高.考虑双IM进行易损性分析可以较为准确地刻画桥墩损伤的状态, 该模型可为后续桥梁加固与风险评估提供更为准确的建议.

5　结语

1) 采用ROC分析方法, 实现了对地震动强度指标的评价, 通过比较发现： 基于两个地震动强度指标的有效性普遍优于单一地震动强度指标的有效性, 可以反应更多地震动的信息.

2) 根据线性组合建立地震易损性曲面, 通过分析发现： 对于PGV与PGV/PGA而言, PGV对桥墩损伤概率的影响要大于PGV/PGA； 对于Sa(T=0.4 s)与Sa(T=2.0 s)而言, 两者对桥墩损伤概率的影响则基本相同.

3) 通过对比地震易损性曲面与地震易损性曲线发现： 在易损性分析中考虑双IM后, 桥墩发生损伤的概率发生一定程度变化, 基于双地震动强度指标的易损性模型能够更为准确地评估墩柱的地震风险.