一种云环境下的虚拟机负载均衡算法
江 伟, 刘漳辉, 邱启荣, 黄启成
(1.福州大学数学与计算机科学学院, 福建 福州 350116; 2.福建省计算机网络与智能信息处理重点实验室, 福建 福州 350116; 3.福州大学科技处, 福建 福州 350116)
0 引言
云计算已经成为引领未来信息产业乃至整个经济社会创新发展的战略性关键技术和基础性创新平台[1], 以一种按需处理的方式, 用于随时随地访问应用程序、 服务和基础设施[2].作为云环境下任务和资源分配的一个重要属性, 负载均衡的相关研究吸引了越来越多专家和学者的密切关注, 并提出了一些优化算法和模型.
基于系统的状态考虑, 可以将负载均衡算法分为静态和动态两大类.静态算法, 如文献[3]提出了一种基于轮转调度的算法 (round robin, RR), 将任务以类似轮转的方式分配给每个节点, 并进行了不同轮转方式的对比; 文献[4]提出了机会均衡负载算法(opportunistic load balancing, OLB), 根据任务的平均完成时间将任务分配给可用的节点, 保持节点处于繁忙状态; 文献[5]提出了一种结合OLB和基于Min-Min的负载均衡算法 (load balance min-min, LBMM)的两阶段调度算法, 以达到提高执行效率, 同时维持系统的负载均衡的目标.动态算法方面, 随着群体智能技术的发展, 遗传算法、 粒子群算法、 蚁群算法等被广泛用于处理动态负载均衡问题.如文献[6]提出了一种结合模拟退火算法(simulated annealing, SA)和果蝇算法(fruitfly optimization algorithm, FOA)的多目标优化算法, 将过载虚拟机上的任务分配到合适的虚拟机上, 在负载均衡的同时, 最小化数据中心的能量开销; 文献[7]提出一种混合元启发式算法 (ant colony optimization with particle swarm, ACOPS), 将主机的内存利用率、 CPU利用率以及磁盘利用率作为优化目标, 其结合了蚁群算法正反馈机制和粒子群算法收敛性快的优势.
目前, 多数负载均衡算法都以虚拟机的CPU、 内存、 磁盘等资源的利用率作为优化目标, 而未考虑虚拟机上总任务执行时长不均衡导致任务总完成时间增加的问题.本研究提出一种结合随机森林分类器的多目标粒子群优化算法(particle swarm optimization with random forest, PSORF), 该算法不仅均衡了虚拟机的CPU和内存的利用率, 也将虚拟机上总的任务执行时长作为优化目标, 以达到均衡虚拟机资源利用率, 同时减少任务总完成时间的目的.仿真实验结果表明, PSORF能够较好地优化虚拟机的负载均衡问题.
1 问题描述
本研究主要解决云环境下负载均衡问题.问题描述如下:
1) 假设任务集合Tasks={taskj|1≤j≤m},m表示任务数量;tm, j、tc, j和trt, j分别表示任务j的内存使用量、 CPU使用量和任务工作时长.
2) 假设Mi、ci分别表示虚拟机i的内存和CPU资源, 且每台虚拟机内存和CPU资源相同, 则资源约束条件如公式(1)所示, 表示分配到虚拟机i上ki个任务的最大内存使用量和CPU使用量不超过虚拟机对应资源总量.
(1)
3) 假设虚拟机集合VMs={VMi|1≤i≤n},n表示云数据中心处理任务的虚拟机数量, 虚拟机VMi负载情况表示为VMi={Mi,ci,rti}.其中,Mi、ci、rti分别表示虚拟机VMi上ki个任务的平均内存利用率、 平均CPU利用率和总工作时长, 如公式(2)所示.定义Mmax=max {Mi|1≤i≤n},Mmin=min {Mi|1≤i≤n},cmax=max {ci|1≤i≤n},cmin=min {ci|1≤i≤n}, RTmax=max {rti|1≤i≤n}, RTmin=min{rti|1≤i≤n}.

(2)
本研究目标为求出任务分配向量S, 均衡各虚拟机的资源使用和总工作时长, 保证在提高虚拟机资源利用率的同时, 降低任务的总等待时间.
2 任务分配模型
2.1 负载均衡模型
由于不同任务需求的资源不同, 在不使用负载均衡优化算法的情况下, 任务被分配到不同的虚拟机上后, 容易出现虚拟机负载不均衡的情况, 虚拟机过载和低载的情况时有发生, 进而降低了资源的利用率和SLA水平.
定义1给定任务分配向量S,Mi、ci和rti分别表示虚拟机集合VMs中第i台虚拟机的平均内存利用率、 平均CPU利用率和总任务工作时长, 使用Max-Min标准化方法对集合{Mi,ci,rti|1≤i≤n}中的数据进行归一化处理, 如公式(3)所示:
(3)
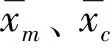
(4)
基于上述定义, 在给定任务分配向量S情况下, 虚拟机集合VMs的负均衡度BD可由公式(5)得到.对于不同的任务分配向量S, BD值越大, 虚拟机集合VMs的负载均衡度越高; 反之, 负载均衡度越低.
(5)
2.2 等待时间模型
假定当任务j被分配到虚拟机i时, 任务j会被添加到虚拟机i的任务队列Q中, 若此时队列Q的长度为l, 则任务j必须等待队列Q中前l-1个任务执行完毕后开始执行.因此, 当虚拟机工作时长不均衡时, 容易造成部分虚拟机上任务的等待时间过长, 延长任务的总等待时间, 从而降低了SLA水平.
定义2假设虚拟机集合VMs中第i台虚拟机上的任务队列Qi={taskj|1≤j≤ki},trt, j表示虚拟机i第j个任务的实际工作时长, 则虚拟机i上第l个任务的等待时长可以表示为:
(6)
所以, 虚拟机i上任务的总等待时长表示为:
(7)
则总任务等待时长表示为:
(8)
其中:n表示虚拟机数量.
3 虚拟机负载均衡策略
3.1 任务分类
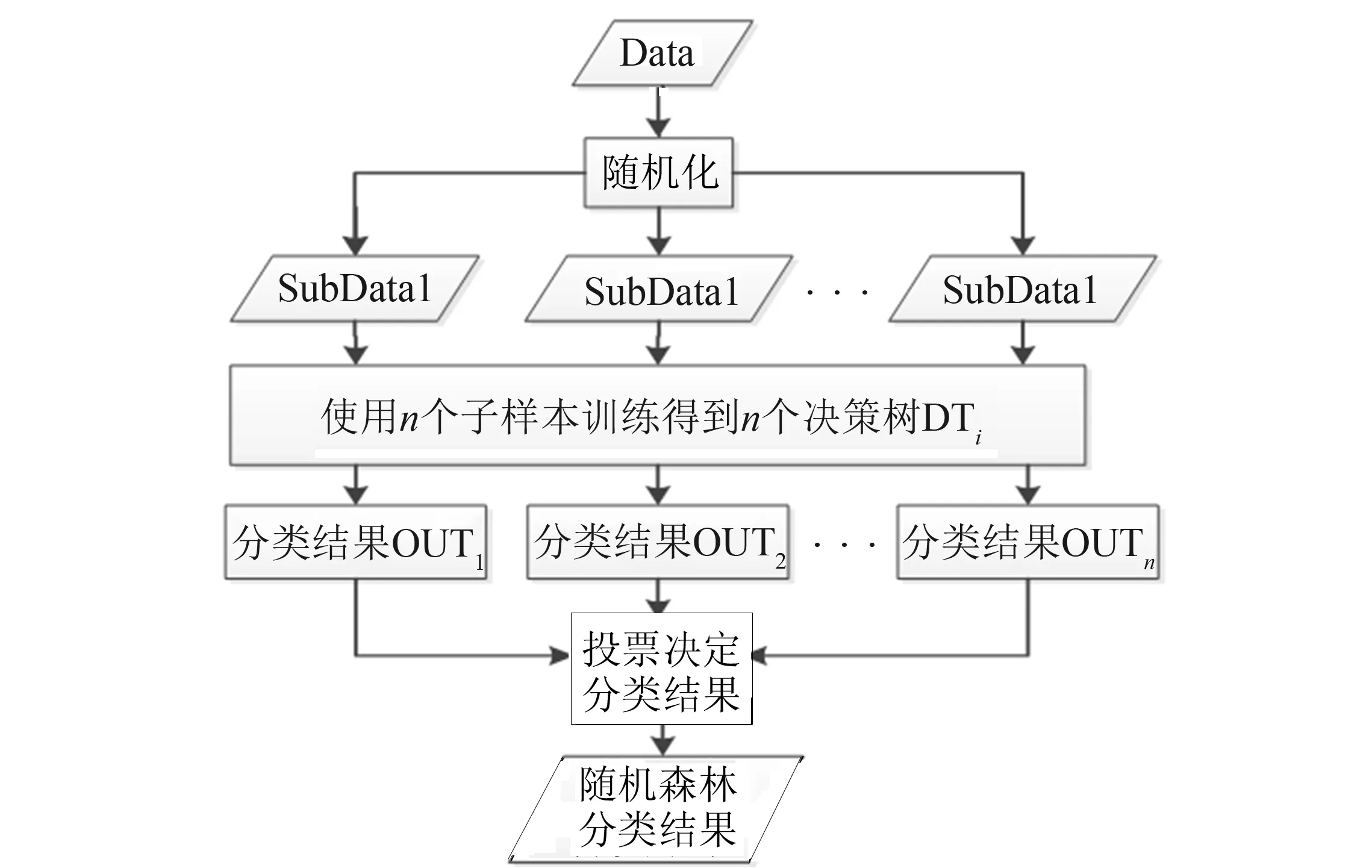
图1 随机森林分类器分类过程 Fig.1 Classification process of random forest classifier
随机森林最早在文献[8]中被提出, 可用于处理分类和回归问题[9].详细过程如图1所示, 将原始数据集Data通过随机化操作重新调整样本顺序; 将随机化后的数据集分为n个子集subDatai; 使用子集subDatai样本训练得到决策树DTi; OUTi表示决策树DTi的输出, 统计分类结果OUTi, 采用投票决定的方式选择得票最高的OUTi作为随机森林分类器的分类结果.
算法采用随机森林分类器对任务进行分类, 通过不同的类目划分出任务的工作时长, 进而达到均衡各虚拟机上任务总工作时长的目的.本研究每个训练样本由六种属性组成task={subTime, reqCpu, reqTime, reqMem, status, runtime}, 分别表示任务的提交时间、 请求的cpu使用量、 请求时间、 请求的内存大小、 状态以及实际的运行时间.根据runtime属性划分出五个区间, 分别表示超短时任务(SST)、 短时任务(ST)、 普通任务(NT)、 长时任务(LT)以及超长时任务(SLT)这五个类目, 类目对应的区间分别为(0, 2 000)、 (2 000, 4 000)、 (4 000, 6 000)、 (6 000, 8 000)、 (8 000, ∞).每个区间任务数为2 000条, 进而得到有10 000条训练样本集合Task, 使用集合Task训练得到随机森林分类器RF.
根据待分配任务的提交时间(subTime)、 请求的cpu使用量(reqCpu)、 请求时间(reqTime)、 请求的内存大小(reqMem)以及状态(status)这五种属性, 通过随机森林分类器RF将任务分类到类目c,c∈{SST, ST, NT, LT, SLT}.
3.2 粒子群优化算法
在粒子群优化算法中, 所有粒子朝着可能解的位置不断聚集.公式(9)、 (10)表示粒子的位置更新策略,Spb, j(t)和Sgb(t)分别表示粒子的历史和全局最优值, 算法持续迭代, 直到满足停止条件.
xij(t+1)=xij(t)+Vij(t+1)
(9)
Vij(t+1)=c1×Spb, j(t)+c2×Sgb(t)
(10)
3.3 适应度函数
本研究中每一个粒子代表一种任务分配方案, 粒子适应度就是粒子编码所对应分配方案的负载均衡度, 适应度值越大, 负载均衡度就越高.
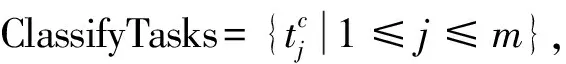
(11)
其中:ki表示虚拟机i上的任务数量.
定义Smax=max {sizei|1≤i≤n},Smin=min {sizei|1≤i≤n}, 使用Max-Min标准化方法对集合{sizei|1≤i≤n}中的数据进行归一化处理:
(12)


类目SSTSTNTLTSLT区间(0, 2000)(2000, 4000)(4000, 6000)(6000, 8000)(8000, ∞)tcsize, j10003000500070009000

(13)
为了降低任务总等待时长, 同时解决虚拟机的负载均衡问题, 根据定义1和定义3, 定义目标函数如下:
(14)
其中:Vc、Vm和Vsize分别表示集合VMs中各虚拟机平均cpu利用率、 平均内存利用率和总工作时长这三种数据的离散程度;r1、r2和r3表示权重系数.
本算法的目标是在迭代次数范围内找到使适应度函数值达到最大的任务分配向量S.
3.4 粒子编码
粒子编码就是将粒子转换为有实际意义的分配方案.本研究中每一个粒子代表一种任务分配方案, 粒子的维度等于待分配的任务数量, 维度的值代表虚拟机编号.假设粒子所表示的解向量P={p1,p2, …,pn},N表示向量P的维数,Ni表示向量P第j维的值, 则Nj=i表示任务j分配到虚拟机i.例如有向量P=(2, 3, 1, 2, 4), 则N1=2表示任务1分配到2号虚拟机上,N2=3表示任务2分配到3号虚拟机上, 相应的N5=4表示任务5分配到4号虚拟机上.
3.5 更新策略
由于粒子群优化算法常用于求解连续值的优化问题, 而本研究的优化目标是求解任务分配向量S, 是一个离散值优化问题, 所以重点在于如何对粒子的位置更新方式进行调整, 使得粒子的位置能与实际的虚拟机编号相对应.本研究采用文献[10]的提出的方法, 重新定义粒子位置和速度更新函数中的加法操作.假设Spb和Sgb分别表示粒子局部最优解向量和全局最优解向量,c1和c2分别表示两者的权重, 这里0 表2 粒子更新策略示例 如表2示例, 假设有5个待分配的任务和3台虚拟机, 虚拟机编号为{1, 2, 3}.在第T轮迭代之后, 得到局部最优解向量Spb={2, 3, 3, 2, 1}和全局最优解向量Sgb={1, 2, 1, 3, 3}.设置c1=0.3、c2=0.7,rdi表示向量R第i维的值,rdi为区间[0, 1]中的一个随机1位小数.当rdi≤c1时, 使用向量Spb第i维的值更新向量V第i维的值; 当rdi>c1时, 使用向量Sgb第i维的值更新向量V第i维的值, 最终得到速度向量V={2, 2, 1, 3, 1}. 算法步骤描述如下: 步骤1基于样本数据集D构建随机森林分类器RF. 步骤3设置实验算法参数: 粒子数量、 最大迭代次数、 权重值c1、c2等, 如表3. 步骤4初始化粒子: 每个粒子第i维的值表示第i个任务被分配到的虚拟机编号, 计算每个粒子的适应度值和编码并保存到该粒子历史最优适应度和编码, 根据每个粒子的历史最优适应度, 选出全局最优适应度和相应编码. 步骤5每个粒子根据更新策略进行粒子更新操作, 并计算更新后的粒子适应度值. 步骤6每个粒子当前适应度值与其历史最优比较, 如果优于历史最优适应度, 则更新该粒子的历史最优适应度以及相应编码. 根据每个粒子的历史最优适应度, 选出全局最优适应度和相应编码. 步骤7如果满足停止条件, 则输出全局最优编码以及最优适应度; 否则, 转到步骤5. 若迭代寻优的结束条件满足, 则将最优粒子的编码解码成任务的一个分配方案, 算法结束. 表3 实验参数设置 本研究采用真实设备的工作负载记录数据来构建和验证负载均衡算法的性能.采用java语言进行仿真实验, 对比了PSO和GA两种经典的群智能算法, 分析两种方法得到的负载均衡度以及任务的总等待时长, 实验参数设置如表3所示, 每种实验重复10次取平均值.实验环境是: Intel(R) Pentium(R)处理器, 主频3.20 GHz, 内存8 GB, 操作系统是Windows 10. 数据集为真实的网络工作负载数据, 来源于(http://gwa.ewi.tudelft.nl/datasets/gwa-t-4-auvergrid)网站, 该网站提供了许多不同的工作负载记录, 并且被广泛地应用于学术领域的研究.该数据集存储了12个月的网络工作负载数据, 并且每条记录都包含了十分完整的属性. 由于本研究提出的算法会在分配任务之前使用分类器对任务进行分类, 所以分类器分类结果的准确度会对负载均衡的结果产生影响.因此, 实验从数据集合Task中随机选取了70%的数据作为训练集, 使用剩余的30%作为验证集, 构建了几种分类器, 分类器的类型与结果如图2所示. 实验比较了几种常用的分类模型, 包括决策树、 随机森林、 朴素贝叶斯、 支持向量机以及线性分类器, 从图2中可以看出, 论文采用的随机森林分类器具有较好的分类准确度. 从数据集D中选取500条记录, 其中属于不同类目的任务各100条, 组成待分配的任务集合Tasks={task1, task2, …, task500}, 并随机化任务顺序.实验对比了PSORF、 PSO和GA这三种算法在得到最优解的情况下, 根据公式(5)计算负载均衡度值DB的大小.参数设置如表3所示, 任务数量从100开始递增至500, 实验重复10次取平均值, 实验结果如图3所示. 图2 几种分类器准确度的比较Fig.2 Comparison of the accuracy of several classifiers 图3 负载均衡度比较Fig.3 Comparison of load balance 从图3中可以看出, 随着任务数的增加, 三种算法的负载均衡度都逐渐上升, 这主要是因为随着任务数量的增加, 任务需求的资源更具有多样性, 这有利于均衡资源的分配.但与此同时还可以发现, 通过PSORF算法得到分配方案的负载均衡度值总是会高于PSO和GA算法, 这主要是由于目标函数的不同, PSO和GA两种算法并没有均衡每台虚拟机上任务总工作时长, 因而降低了其分配方案的负载均衡度. 假设Queuei表示分配到虚拟机i上的任务队列, 则根据不同的分配向量S可以得到不同的任务分配队列Queuei.本研究假定每台虚拟机顺序执行队列Queuei上的任务, 则根据公式(7), 不同的任务队列Queuei得到的总任务等待时间waiti也是不同的. 因此, 实验对比了PSORF、 PSO和GA这三种算法在得到最优解的情况下, 根据公式(8)计算任务的总等待时间的大小.本实验的任务集合与4.4节实验相同, 参数设置如表3所示, 任务数量从20开始递增至100, 实验重复10次取平均值, 实验结果如图4所示. 从图4中可以发现, 随着任务数量的增加, 任务的总等待时间逐渐递增, 且PSORF算法总能得到最小的等待时长, 这说明PSORF算法确实能有效缩短虚拟机上任务的总等待时间.此外还可以发现, 随着任务数量的增加, 三种算法得到的等待时间的差距也逐渐增加, 这主要是因为任务数量的增加使得解空间增大, PSORF算法由于目标函数的不同, 更可能得到最优的分配方案. 为了验证算法的收敛性, 实验对比了使用PSORF、 PSO和GA这三种算法最优解的迭代次数.该实验的任务集合与4.4节实验相同, 参数设置如表3所示, 实验重复10次取平均值, 实验结果如图5所示. 从图5中可以看出PSORF算法最优解的迭代次数略好于PSO算法, 这是由于两者目标函数不同的影响, 但总体上两者收敛性并无显著差异.然而GA算法随着任务数量的增加, 最优解的迭代次数并无明显变化, 这说明算法并不能在实验设置的最大迭代次数内收敛, 所以与另外两种算法相比, 其收敛性较差. 图4 等待时间的比较Fig.4 Comparison of waiting time 本研究将每台虚拟机上任务的总工作时长也作为一个优化目标加入到目标函数中, 使得算法在均衡虚拟机的内存使用量和CPU使用数量的同时, 也均衡总的工作时长, 进而降低了任务的等待时间.为了实现这一目的, 在PSO算法的基础上, 结合了随机森林分类器, 在任务通过PSO算法分配之前使用分类器将任务分类到5个不同的类目, 不同的类目代表了不同的任务长度, 进而使PSO算法能对虚拟机上任务的总工作时长进行均衡.最后, 实验对比了两种经典的群智能算法PSO和GA, 实验结果表明本研究提出的PSORF算法提高了负载均衡度, 同时也降低了任务的总等待时间.在未来工作中, 可以采用更多的数据集来验证算法的适用性, 由于任务的分类准确度会对负载均衡的结果产生影响, 所以寻找更合适的分类方法将是一个研究方向.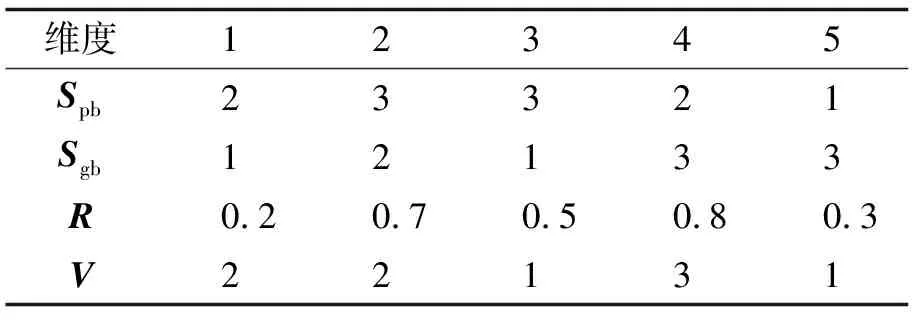
3.6 算法描述
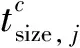

4 仿真实验
4.1 实验环境与参数设置
4.2 数据集
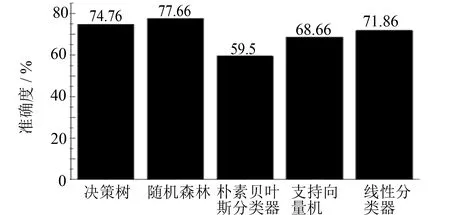
4.3 分类器结果比较
4.4 负载均衡度比较

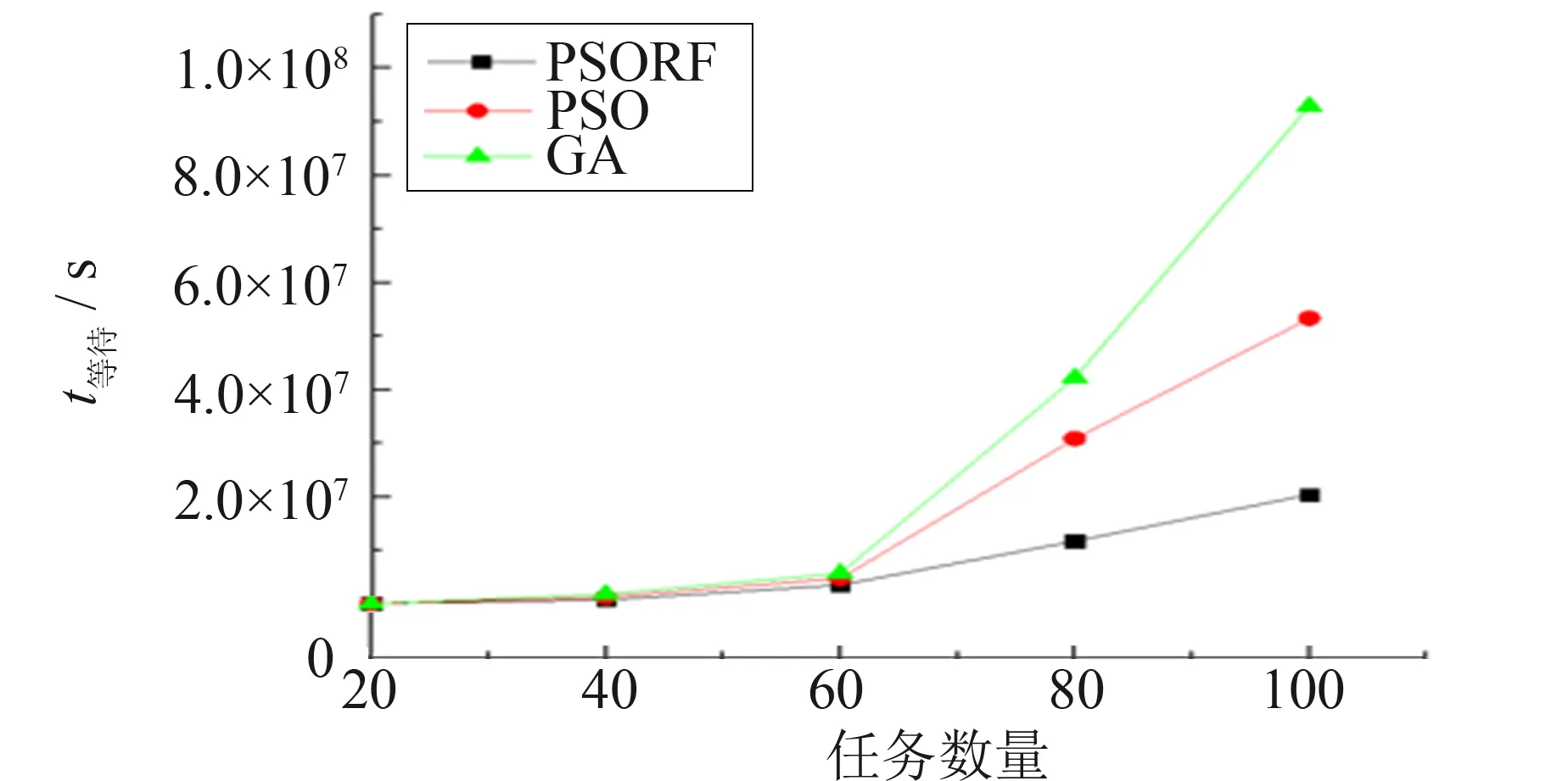
4.5 任务总等待时间比较
4.6 收敛性比较
5 结语
——国外课堂互动等待时间研究的现状与启示

