约束三段法检测全站仪加常数的分析

李菁文　左凌霄　吴迪晟　严德圣　李玉宝　钱声源

(1.东南大学成贤学院，江苏 南京　210088;　2.东南大学，江苏 南京　211189)

1　概述

全站仪是一种可以测量水平角、垂直角、距离、高差测量等功能于一体的测绘仪器系统。同时，需要时可由绘图仪自动绘出所需比例尺的图件，由打印机打印出所需成果表册。这样使测绘工作的外业和内业有机的连接起来，实现了真正的数据流。在全站仪测量前，必须要对仪器定期进行检验或检测，进而可以得出某些参数，可用于校正仪器或某些测量成果。全站仪的仪器加常数C是受仪器测距系统本身的加常数C1和所配用反射镜的测距常数C2的联合影响，而对其检测是仪器定期检测的项目之一。由于各种复杂的因素，致使所测量的距离的端点与仪器和反射镜的中心不一致而产生误差，该误差在一定的时期内基本稳定，故称其为常数，改正数为C。每个仪器的C值是不完全一样，因此需要各自独立按时检测，以确保测量的精确性。关于全站仪的仪器加常数C的检测，一直是与仪器乘常数R一并按“六段基线比较法”检验的。

在导线测量时，由于C值发生了变化或C值不正确导致点位中误差超限，在较短距离的测量时比例误差显得影响不大。当在较短的时间内，C值可被当做是常数，但相对于较长的时间来说，C值本质上是变化的。C值变化主要的原因有内部结构的缺陷、外界环境的变化等影响。因此，当对C值有存疑时，应研究一种因地制宜、又保证检测精度的方法来进行随时检测。

本文研究“约束三段法”检测C值，能很好地优化C值产生的误差所带来的问题，并在实际的运用当中取得了令人满意的结果。

2　“约束三段法”的理论依据

2.1　场地布设

如图1所示，首先在平坦的地上选出3分段(即d1,d2,d3)作为C值的检验场地，总长为D。

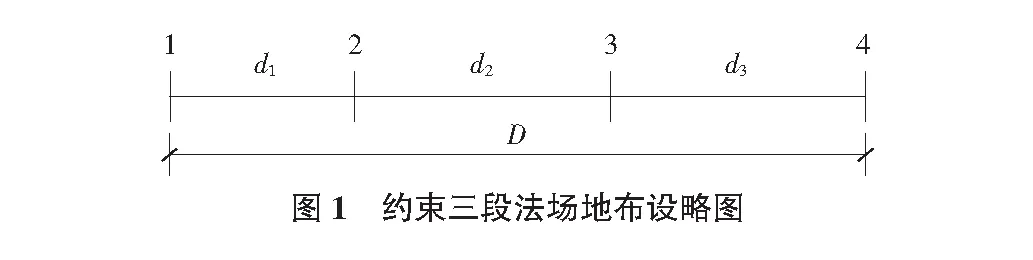
分别在1点、3点设站，在2点、4点设棱镜，测出平距观测值分别为D′,d1′,d2′,d3′。通过对各项误差的改正，距离观测值可组成以下的等式:

D′+C+RD′+ΔDφ=(d1′+C+Rd1′+Δd1φ′)+(d2′+
C+Rd2′+Δd2φ′)+(d3′+C+Rd3′+Δd3φ′)=
C+∑di′+R∑di′+∑Δdi′

(1)

其中，仪器加常数为C；乘常数系数为R；周期误差改正数为ΔDφ′,Δdiφ′。由式(1)化简可得：

(2)

因为周期误差改正数的特性是在一个精测尺长度内呈正弦函数变化规律，则规定对检测场地的检测距离加入“约束条件”，即：

1)全长距离D=(N0+x)×u；

2)分段距离d1=(N1+x)×u；

3)分段距离d2=(N2+3/4)×u；

4)分段距离d3=(N3+1/4)×u；

5)N0,N1,N2,N3都是自然整数，x为任意数，u为精测尺长度，且N0=N1+N2+N3+3/4+1/4。

当设置了“约束条件”后，这样就能在其测算中自动抵消了周期误差改正数。

ΔDiφ=Asin(φ+θi)

(3)

式(3)为周期误差改正数公式，其中A为振幅;φ为初相位角；θi=(di/u-int(di/u))×360°,精测尺u范围内距离长度的变化导致其一致发生变化。因此可以得出,周期误差的改正数为:

ΔDφ=Δd1φ′,Δd2φ′=-Δd3φ′

(4)

由图1可知，距离观测值有以下关系:

(5)

将式(4),式(5)代入式(2)，则有:

(6)

式(6)说明在检测加常数时，周期误差改正、乘常数改正是可自行抵消的；同时也可自行消除掉比例误差，从而提高了检测的效率和精度。这有效地避免了这些改正参数本身的误差对C值的影响。可显著地消除其余系统误差，从而使C值更加接近真值。上述展示出了三段法结合“约束条件”的优点，故将该法称为“约束三段法”。在实际检测加常数时，由于周期误差一般比较小，故各段长度基本按照上述的原则进行分配，在实际操作中用皮卷尺沿直线丈量定点布设场地且各段的长度取值约为几十米，也就是N0取10左右。

2.2　精度分析

由于各段的距离差别不大，因此可设式(6)中各观测值的测距中误差相等为md。按误差传播定律、由(6)式得仪器加常数C的检测中误差为:

(7)

按照测绘作业的要求，加常数的中误差mC须不大于观测值中误差的1/2为好，即有:

(8)

由于没有足够的多余观测，所以按式(7)计算时，并不能满足式(8)的要求。需增加测段数或多余观测，解决这个矛盾。本文采用多测回观测的方法增加多余观测。设测回数为M，则有:

(9)

对照式(8)，式(9)两式，取最不利的情况，可知检测距离的观测测回数M应为4。

检测时，一般对每个距离独立观测4个读数为一个测回，当距离稳定时可减少测回中的观测次数。这样对每个距离独立观测4个测回，即满足上述的要求，也可根据测距的稳定程度自行确定测回数和个数。

2.3　应用分析

1)采用“约束三段法”检测C值。

检测仪器GTS-102N全站仪(NO：220680)，配用单个反射棱镜，u=10 m；按“约束三段法”在两个不同长度的场地上检测C值。在设计各段的检测长度时，应根据“约束条件”将场地分别为，Ⅰ场地：N0=3,N1=1,N2=1,N3=0,x=0；Ⅱ场地：N0=5,N1=2,N2=1,N3=1,x=0；Ⅲ,Ⅳ等，依次用皮卷尺沿直线丈量定点(精度为cm数量级)，共布设4个长度分散的场地，以考察在不同距离时C值可靠程度。其测算结果见表1。

取在4个场地检测的中数C=+0.6 mm，mC=±0.4 mm作为该仪器的最后结论。

2)方差分析。

表1中所列的结果存在差别。现通过方差分析，以判断C值结果是否有显著的差别。

经计算，C值检测组内和组间方差总和分别为：

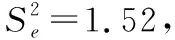
以自由度12，3取显著性水平α=0.05，查F分布表，得：F0.05=3.5。

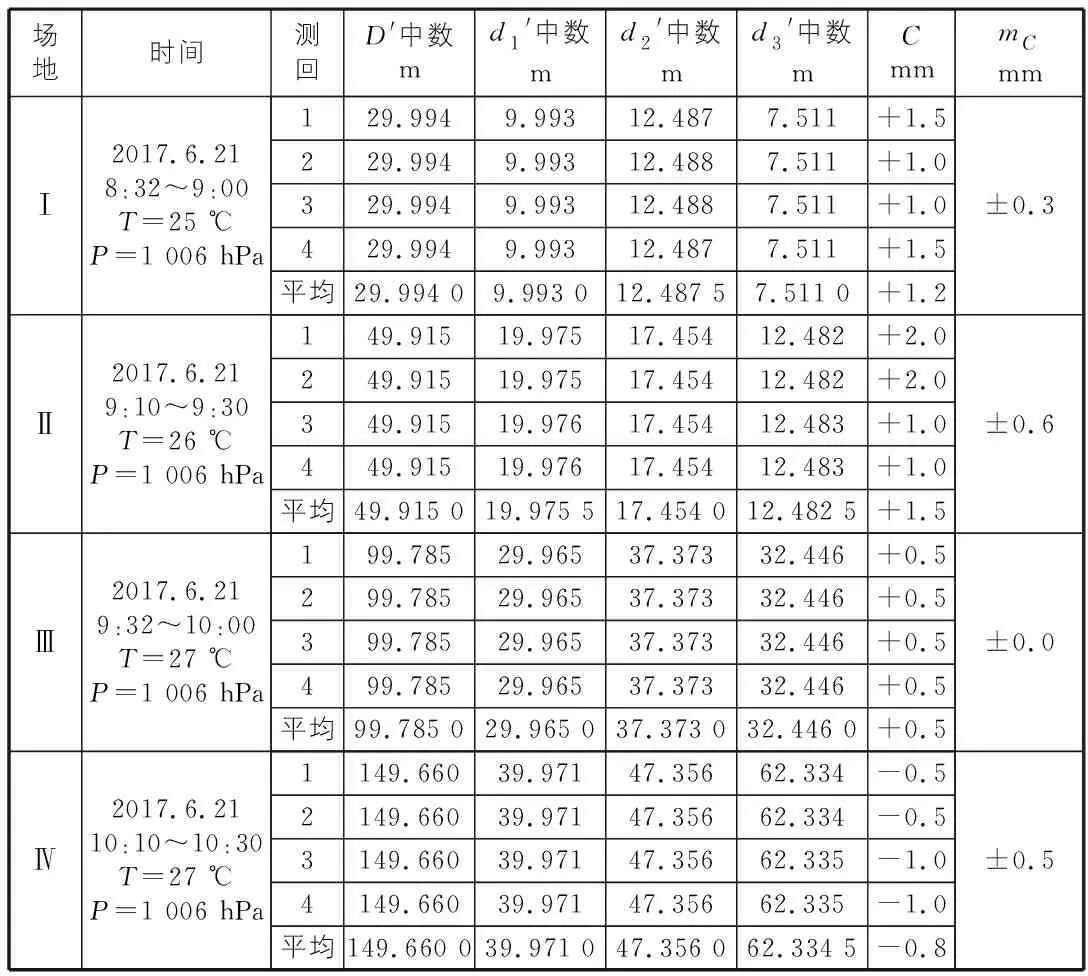
表1　约束三段法检测加常数记录计算表

结果表明在4个场地中所检测的结果都独立、有效；C值实际的差异是由于正常的测量误差以及环境变化的因素影响的，而理论公式模型是正确的。

3　结语

本文研究的“约束三段法”检测C值的方法，其优势和创新点在于：一是对已知的基线场地依赖性不强；二是检测手段简便；三是简化了许多麻烦的工作，如对观测值的各种改正等；四是进一步对检测的效率和精度有明显提高；五是在独立、多测回观测下，所检测得出的C值更加可靠、精确度高。在每期作业前后或对一起的常数存疑时，可随时采用该法检验。对于测绘生产是很有利的。检验时的场地布设的长度最好与测量作业的长度吻合一致比较好。