基于数字拟合数据方法的金属选矿产品结构预测与优化
刘 颖
(陕西交通职业技术学院,陕西 西安 710018)
0 前 言
金属选矿产品结构预测与优化是在既定的产品质量要求下,寻求最佳的分选方案,以为选矿产品的开采、加工工艺提供决策支撑,目前国内外研究多在最大化经济效益的约束条件下,通过优化重介质、浅槽及螺旋等分选机的局部流程,来实现整体优化,主要是以理论数据为依据的定性分析,对于各分选系统选矿产品预测和生产的实践指导性较差,针对此,本文针对精矿产品与最大经济效益之间的直接关联性,基于不同的预测目标和优化问题,通过产品目的与分配率的求解,进行分配曲线的拟合,同时用Matlab编程,运用差分进化算法对各个数学模型进行寻优计算,获取拟合差最小的数学模型,将这种模型作为分配曲线的最佳拟合模型,并运用平移分配曲线得到选矿产品的各个密度级分配率,建立各分选系统的产品预测模型,由此,完成了金属选矿产品的整体预测,提升了模型的普适性,最后,以最大效益为目标采用优化算法对各分选方案进行对比分析,获得结构优化优化模型,并经验证,该模型精准度较高。
1 数学拟合数据方法
分配曲线是根据金属矿各分选工艺的原始数据,计算产品的产率,获得各个密度级的分配率[1],得出了密度与分配率的关系曲线,其是重力选矿效果的直接体现。
1.1 产品实际产率
选矿产品实际产率多采用格氏法,也即最小二乘法进行计算,但在三产品产率计算时其复杂度过高,为此将其转化为求解最优化的问题,计算公式为:
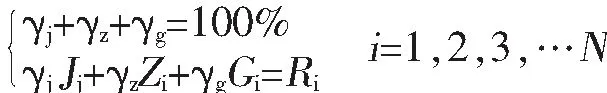
(1)
式中:γj、γz、γg分别为精矿、中矿、尾矿的产率,%;Ji、Zi、Gi、Ri分别为精矿、中矿、尾矿及原矿各密度级的含量,%。
采用操作简单、求解成功率高的1stOpt 5.0曲线拟合软件方法规划求解的产品产率,其目标函数确定的依据为:所有产品密度级实验值和计算值的偏差平方和最小,公式为:
(2)
式中,Ri′是入料的各个密度级实测产率值。
1.2 各个密度级的平均密度
可选性曲线手工绘制过程中,多以各个密度级的算数平均值来表示平均密度值,且选矿产品在经过洗选后质量总和不变,由此得出各密度级的密度均值为:

(3)
y=100×{b1+b2×ρ+b3×th[b4×(ρ-b5)]}
(4)
公式(4)中,ρ、y分别代表密度与浮物的累计的产率。将公式(3)代入(4)即可获得:
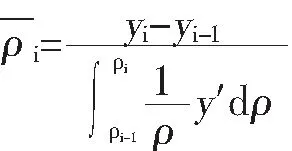
(5)
根据金属矿厂原始资料数据,利用Matlab编程,得到中间的密度级别的平均密度,据此,可推导出端部的密度。
1.3 分配率
根据单机检测数据,结合计算所得的产品实际产率,即可获得相应的分配率,以动力金属矿三产品旋流器为例,计算所得的一、二段重产物分配率为:
(6)
上式中,J、Z、G为对应密度级的三产品各自含量。
2 分配曲线进行拟合的模型
分配曲线进行拟合的模型存在反正切、双曲正切、指数、洛伦兹累计等多种类型[2],这些函数具有普适性,但如果入料金属矿材料比较特殊时,拟合误差则可能会较大,且其为非线性函数,格氏法依赖于预先给定的初始拟合参数,但由于相关浮沉资料数据未知,无法获取初始的参数值,会影响拟合结果精度,为此,应该选择无需预先设定初始参数值的最优化方法进行迭代计算,求解最优化模型的最小拟合误差,以分配率计算值与实验值的偏差平方和最小作为目标函数,可定义为:
(7)
式中,yi、yi′分别为实测已知数据及拟合的计算值,n代表实验次数,σ代表拟合误差值的最终结果,该值越小,曲线拟合效果越好,既定值不能大于曲线纵坐标尺度的5%[3],因分选工艺中的原始资料不同,拟合误差存在较大差别,用Matlab软件建立各个数学模型时,需要根据各类模型函数寻求最小拟合误差,以三产品重介质旋流器的原始数据资料为准,结合上述分配曲线拟合相关数据的计算方法,可获得曲线拟合数据,如表1所示。

表1 分配曲线拟合数据计算
差分进化算法具有编码方便、全局收敛及记忆最优解能力强等优势[4],为此,采用该算法进行分配曲线拟合的寻优计算,结合上述相关的密度、产率及分配率等计算方法,利用Matlab软件对低密度段分配曲线进行编程,分别采用10种数学模型函数,获得拟合结果如表2所示。

表2 各类分配曲线数学模型拟合结果
表2中,a、b、c、d、e是各模型函数中由左至右参数的表达,对同一组数据运用不同的数学模型进行拟合,所得的拟合误差值浮动范围较大,取其中最小拟合误差的数学函数作为分配曲线拟合的数学模型,通过上述拟合结果的对比,采用Extreme Value Cumulative数学函数进行拟合所得的误差仅为2.031 2%,为此,将这种数学函数进行分配曲线拟合。
3 各分选系统的产品预测模型
因为入料的密度构成与分配曲线之间存在较小的关联性,在原矿石密度偏离既定要求时,可结合可选性曲线计算轻、中产物的产率、品位,而后利用分配曲线的平移即可获得所有密度级的分配率[5],进而获得选矿产品的各密度级品位。以各密度级的平均密度与分配率作为分配曲线的横、纵坐标,金属矿重介质各分选环节中分配曲线的平移,需要根据可能偏差E值不随分选密度改变而改变的特性来实现,其中,分配曲线的斜率没有变化,通过对平均密度的横坐标进行移动,由此得到新的分配曲线;而水介质各分选环节中平移分配曲线,则需依据不完善度I值的固定性来实现,其中,分配曲线斜率发生了改变。在利用数据方法对分配曲线进行拟合时,通过密度坐标的转换方法即可完成分配曲线的平移,E值固定下,计算公式为:
δ′=δ-δ2+δ1
(8)
E值不变时,计算公式为:
δ′=(δ-1)(δ1-1)/(δ2-1)+1
(9)
上式中,δ′、δ分别为转换后及实际分配曲线的密度坐标,δ1、δ2分别为平移前后的分选密度。
据此,各分选系统选矿产品结构的数质量预测算法为:
Gi=Yi·f(xi)
(10)
Gsum=ΣYi·f(xi)
(11)
(12)
Ji=Yi-Gi=Yi-Yi·f(xi)
(13)
Jsum=Σ(Yi-Yi·f(xi))
(14)
(15)
上式中,xi、f(xi)代表密度级、产品每个密度级的分配率,Ai代表入料、尾矿与精矿各个密度级的品位设定值,Gi、Ji、Yi代表尾矿、精矿与入料这3种产品的第i密度级的产率,Gsum、Jsum代表尾矿和精矿的产率,AG、AJ为尾矿和精矿的品位。
4 金属选矿产品的结构优化
选矿产品结构优化是一个涉及多参数的非线性问题,根据金属矿厂工艺流程特点,并融合原矿数据、分选工艺及市场条件等因素,可将其归为分选密度最优化问题[6],也即通过在线调节分选密度,求解出精矿、中矿及尾矿的品位及产率,进而拟定相应的产品预测方案,而后采用优化算法进行最优生产方案的确定,以实现经济效益的最大化,三分选工艺的选矿产品结构优化模型为:
maxF(δ)=JPJ+ZPZ+GPG-C1-C2
(16)
上式中,maxF(δ)、δ分别为最大经济效益、分选密度,J、Z、G、PJ、PZ、PG分别为三分选产品精矿、中矿及尾矿的产率及价格,价格由产品品位决定,C1、C2分别为原矿价格、各产品加工费综合,为已知常数项,实际运算中,精矿价格在特定范围内浮动,剔除影响价格的粒度因素,仅计算不同品位条件下精煤价格,当品位介于50%~60%之间时,品位每变动5%,精矿价格随之变动1 000元[7],将浅槽、旋流器、螺旋分选机等不同分选环节的生产成本相应的设定为28元/t、19元/t、15元/t,入料的成本费也将粒度因素剔除,设定为2 500元/t,具体如表3所示。

表3 产品价格及加工费用
以旋流器分选机为例,选矿产品回收率a为变化参数,在不同分选工艺下,所获经济效益存在差异,将其设定为寻优的参数,潘家冲铅锌矿石分级筛后原矿粒级为3类:50 mm、50~100 mm、<150 mm,分别进入浅槽、旋流器及螺旋等分选系统之中,根据以上目标函数,利用1stopt软件编程,以最大经济效益为目标,先后运用了DE算法(差分进化算法)和PSO算法(粒子群算法)进行运算,获取各分选工艺中最优分选密度、精矿品位及产率,从而精准判定末原矿石回收率的不同变化对最终产品经济效益的影响,运算过程中,将初始种群和允许的收敛误差判断均设定为50,因算法种群初始值设定不同,所得的结果存在一定误差,为达到最优结果,进行了3次运算,结果如表4所示。

表4 两类算法所得结果
根据上表可知,差分进化算法进行了3次运算,平均迭代的次数是13.67,标准差为0.83,3次运算平均利润为127.51元/t,标准差为0.02元/t,螺旋分选机与旋流器的最优分选密度没有变化,在小数点后3位才能表现出差异,浅槽分选机的最优分选密度均值为1.71 g/cm,标准差为0.01 g/cm,精矿品位也均未发生变化,均值为7.63%,精矿产率3次运算结果不同,均值为88.14%,标准差为0.01%,上述运算所得结果均在误差允许范围内,算法的运算精准度较高。而相比之下,采用粒子群算法所得的平均迭代次数为18.00,运算所得的平均利润为127.56元/t,标准差为0.28元/t,螺旋分选机的最优分选密度均值为1.80 g/cm,标准差为0.02 g/cm,而浅槽、旋流器两类分选机的最优分选密度均值没有改变,均值各为1.70 g/cm、1.76 g/cm,取小数点后三位才能获得差异,精矿灰分及精准产率的均值分别为7.61%、88.11%,对应的标准差分别为0.01%、0.02%,运算所得结果的标准差均小于既定误差,但差分进化算法的迭代次数及利润均值更优,且标准差更小,也即其计算效率和精度更优。
5 结 语
针对金属矿厂选矿产品结构预测在优化矿石资源利用、获取最大经济效益中的重要性,通过选矿原始资料的整理计算产品的分配率和密度相互关系,进行分配曲线拟合,引入差分进化算法求解各类模型的曲线拟合参数,获取最小拟合误差以确定分配拟合曲线数学模型,以此为基础,构建基于不同预测目标和工艺流程下的预测模型,并以最大经济效益为目标,通过分选密度的寻优计算建立优化模型,计算了浅槽分选机、旋流器与螺旋分选机3种分选系统的最优分选密度,同时计算了的精矿精煤产率和品位的最终值,确定了产品的最佳生产工艺,为选矿产品工艺优化、生产规划提供了良好支撑。

