无刷直流电机的反演自适应动态滑模控制
苗敬利 井爽
摘 要: 无刷直流电机在工作中容易受到系统的外部干扰和参数摄动的影响,根据滑模变结构具有快速响应、鲁棒性好、物理实现简单等优点,可以将滑模变结构控制应用于无刷直流电机中。为了有效地降低无刷直流电机的抖振现象,提出动态滑模方案。同时将自适应技术和反演控制相结合运用到动态滑模方案中,可以实现不确定系统的无抖振滑模控制。仿真结果证明了两种方案的正确性。
关键词: 无刷直流电机; 反演自适应; 动态滑模; 动态切换函数; 抖振; 滑模变结构
中图分类号: TN876?34; TM3 文献标识码: A 文章编号: 1004?373X(2018)13?0119?04
Abstract: The brushless DC motor in working is easily influenced by external disturbance and parameter perturbation of the system. Since the sliding mode variable structure has the advantages of fast response speed, high robustness and simple physical implementation, the sliding mode variable structure control can be applied to the brushless DC motor. A dynamic sliding mode scheme is proposed to reduce the buffeting of the brushless DC motor effectively. The adaptive technology and backstepping control are combined, and used to the dynamic sliding mode scheme, which can realize the sliding mode control without buffeting for the uncertain system. The simulation results show that the two schemes are correct.
Keywords: brushless DC motor; backstepping adaptive technology; dynamic sliding mode; dynamic switching function; buffeting; sliding mode variable structure
0 引 言
无刷直流电机(Brushless DC Motor,BLDCM)具有效率高、响应快、转矩大和惯性低等优点,已经在各个领域中广泛应用[1?3]。理想的电机调速系统应具有高精度的稳态、快速度的响应、较强的抗干扰能力等特点,因此需要高性能的控制策略[4?5]。
由于滑模变结构具有响应速度快、鲁棒性好、物理实现简单等优点,因此得到了广泛应用。滑模控制也验证了其性能。但是,本质上滑模变结构控制在开关特性不连续的情况下将会引起系统出现抖振现象,所谓抖振就是在光滑的切换面上叠加了一种波动的轨迹[6]。抖振文献[7]在无刷直流电机的调速系统中应用了趋近率法的滑模变结构,不仅有效抑制了超调量,而且响应速度快,并具有很好的鲁棒性。文献[8]在无位置传感器的BLDCM控制系统中应用了滑模变结构既对系统控制的准确性产生一定的影响,又会加大能量的消耗,从而破坏系统的性能,甚至使系统产生振荡或者损坏控制器部件[2]。而文献[9]将模糊控制与滑模控制相结合,仅仅改善了系统的抖振。
为了能够有效地削弱滑模控制的高频抖动现象,使用动态滑模控制,同时将自适应技术与反演控制方法相结合,通过设计新的切换函数,采用动态滑模控制算法可以实现不确定系统的无抖振滑模控制。
1 无刷直流电机数学模型[10]
电机相电压方程式如下:

4 系统仿真与分析
采用Matlab/Simulink工具对无刷直流电机控制系统建立仿真模型,并分别对动态滑模控制算法和反演自适应动态滑模控制算法进行仿真试验,同时验证这两种控制算法的有效性和可行性。仿真中所用無刷直流电机的系统参数设置为:阻尼系数[B=]0.000 2 N·m·s/rad,极对数[np=1],定子绕组电阻[R=1] Ω,针对无刷直流电机中的[J]和[B]的值对应于一阶系统中 [θ=0.12],转动惯量[J=0.05] kg·m2,无刷直流电机的转速[ω]的初始值为0对应于一阶系统中[x(0)=0]。反演自适应动态滑模控制器的参数为:[c1=2],[θ1]和[θ2]的初始值取[0 0],电机空载启动,进入稳态后[t=]0.2 s,外加负载信号[TL=]1 N·m。
为了验证本文设计的控制器的控制效果,把该控制器与传统的PID控制器分别用在无刷直流电机的模型中进行仿真控制,所用的PID控制器的参数定为:[Kp=5],[Kd=0.001],[Ki=0.01]。假定给定转速为1 250 r/min,在三种控制算法下所得响应曲线如图1~图3所示。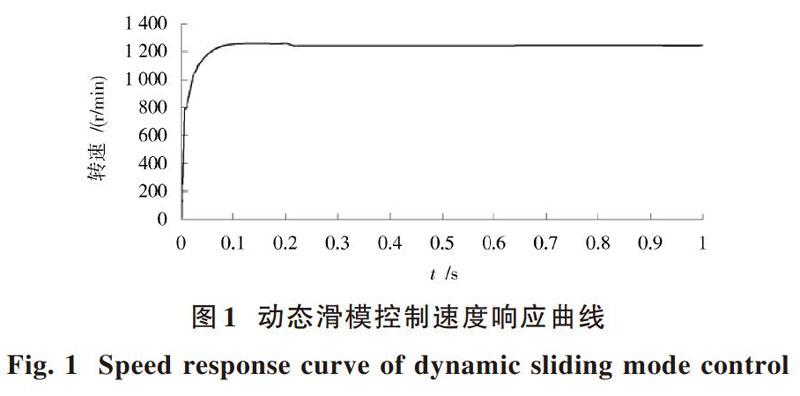
比较图1和图3可知,动态滑模控制算法相比于PID控制算法,跟蹤速度快,超调量变小,有限地降低了抖振,从而证明动态切换函数滑模控制具有可行性。
比较图2和图3可知,反演自适应动态控制算法相比于PID控制算法,快速跟踪,并且超调量也更小,并且在负载突然改变时转速没有明显的变化,因此证明反演自适应动态控制比PID具有更好的可行性和稳定性。
通过比较图1,图2可以看出反演自适应动态滑模控制算法的响应速度快,在负载突变的时候,转速没有明显的变化。动态滑模控制算法刚开始响应速度慢。在负载突变的时候,转速有点变化。反演自适应动态滑模控制的消抖能力强,鲁棒性强,对过程参数的变化以及对未建模部分的动态过程不敏感。因此在负载突然改变时转速没有明显的变化。
由于运行过程中电机的温升会增大,绕组的电阻也会增加,这些因素都会影响电机的参数。比如定子绕组的电阻增大20%,即[R=]1.2 Ω时,电机应用反演自适应动态滑模控制算法时相应转速响应曲线如图4所示。
由图2和图4可知,当电阻增大时,电机应用反演自适应动态滑模控制算法的转速响应曲线基本没有发生变化,说明电机
参数的变化对这两种控制算法影响不大,反演自适应动态滑模控制算法都具有较好的鲁棒性。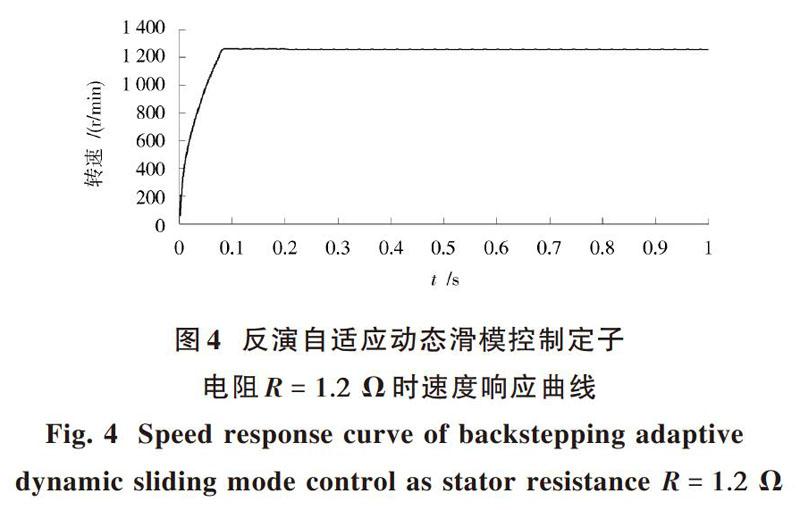
5 结 论
本文利用Matlab/Simulink对无刷直流电机控制系统进行控制算法仿真实验分析,分别得到了反演自适应动态控制的仿真图形和动态滑模控制算法仿真图形,将这两种控制算法分别与PID控制算法相比较,证明了这两种控制算法可以快速跟踪减小超调量。但是将反演自适应动态滑模控制算法与动态切换函数滑模控制算法相比较,发现反演自适应动态滑模控制算法具有较快的响应速度,能更有效地消除抖振现象。也得出反演自适应动态滑模控制算法能够使整个闭环系统具有更好的鲁棒性。
参考文献
[1] 张勇,程小华.改进的BLDCM直接转矩控制系统仿真研究[J].计算机仿真,2014,31(1):323?327.
ZHANG Yong, CHENG Xiaohua. Improvement of BLDCM direct torque control system simulation [J]. Computer simulation, 2014, 31(1): 323?327.
[2] BORA T C, COELHO L D S, LEBENSZTAJN L. Bat?inspired optimization approach for the brushless DC wheel motor problem [J]. IEEE transactions on magnetics, 2012, 48(2): 947?950.
[3] 李宏,王崇武.永磁无刷直流电机模糊自适应控制器设计[J].计算机仿真,2011,28(2):209?212.
LI Hong, WANG Chongwu. Permanent magnet brushless DC motor fuzzy adaptive controller design [J]. Computer simulation, 2011, 28(2): 209?212.
[4] 夏长亮,方红伟.永磁无刷直流电机及其控制[J].电工技术学报,2012,27(3):25?34.
XIA Changliang, FANG Hongwei. Permanent magnet brushless DC motor and its control [J]. Transactions of China electrotechnical society, 2012, 27(3): 25?34.
[5] 杨孝敬,林青松.基于PSD的多电机速度伺服驱动控制研究[J].计算机测量与控制,2013,21(11):2994?2996.
YANG Xiaojing, LIN Qingsong. Research on multi?motor speed servo control based on PSD [J]. Computer measurement and control, 2013, 21(11): 2994?2996.
[6] 李林杰,焦振宏,时建欣.基于滑模变结构控制的对转无刷直流电机调速系统[J].微特电机,2010,38(10):44?47.
LI Linjie, JIAO Zhenhong, SHI Jianxin. Contrarotating brushless DC motor speed control system based on sliding mode variable structure control [J]. Micro & special motor, 2010, 38(10): 44?47.
[7] LONG B, ZHOU H B, CAO B G, et al. Position tracking controlling system of sensorless BLDCM by using MRAC [C]// 2007 IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications. [S.l.]: IEEE, 2007: 1?5.
[8] 李春华,孙约,罗琦.非线性系统的反演自适应动态滑模控制[J].计算机工程与设计,2009,30(1):185?187.
LI Chunhua, SUN Yue, LUO Qi. The inversion adaptive dynamic sliding mode control of nonlinear system [J]. Computer engineering and design, 2009, 30(1): 185?187.
[9] SONG H, YU Y, YANG M, et al. A novel SMC?fuzzy speed controller for permanent magnet brushless DC motor [C]// The Eighteenth IEEE Applied Power Electronics Conference and Exposition. [S.l.]: IEEE, 2003: 281?285.
[10] 苗敬利,邹靖.基于动态Terminal滑模控制的无刷直流电机系统研究[J].制造业自动化,2014,36(11):61?64.
MIAO Jingli, ZOU Jing. Research about a system of the brushless DC motor based on dynamic terminal sliding mode control [J]. Manfacturing automation, 2014, 36(11): 61?64.
[11] 刘金琨.滑模变结构控制Matlab仿真[M].北京:清华大学出版社,2015.
LIU Jinkun. Matlab simulation for sliding mode control [M]. Beijing: Tsinghua University Press, 2015.

