基于改进TPSN和卡尔曼滤波的时间同步算法
胡爱华 邓中亮 张耀
摘 要: 给出一种基于改进TPSN和卡尔曼滤波提高TDOA定位中时间同步精度的方法。TDOA定位中,信号接收设备之间的时间不一致性,最终将反映到定位解算方程中的距离测量上,因此,信号接收设备之间的精确时间同步成为基于TDOA定位的核心技术之一。在比较了多种网络同步协议的基础上,改进主从节点间的TPSN同步协议。另外,针对定位系统中各时钟存在时钟偏移和时钟偏移率的缺陷问题,结合时钟偏移和时钟偏移率的分布特性,利用卡尔曼滤波算法进行时间同步误差的纠正。仿真结果表明,该算法能明显降低主从时钟之间的时间偏差。
关键词: 时间同步; TDOA; 时钟偏移; TPSN; 卡尔曼滤波; 同步精度
中图分类号: TN92?34 文献标识码: A 文章编号: 1004?373X(2018)13?0005?05
Abstract: A method based on improved TPSN and Kalman filtering is presented to improve the time synchronization accuracy in TDOA location. Time inconsistency between signal receiving devices will ultimately influence on the range measurement in positioning resolving equation, so the precise time synchronization between signal receiving devices becomes one of the core technologies based on TDOA location. On the basis of comparing several network synchronous protocols, the TPSN synchronous protocol between master and slave nodes was improved. The method of estimating the clock skew and clock drift rate is studied to overcome the defects existing in each clock in location system. The Kalman filtering algorithm is used to correct the time synchronization error in combination with the distribution characteristics of clock skew and clock drift rate. The simulation results show that the proposed algorithm can obviously reduce the time deviation between master and slave clocks.
Keywords: time synchronization; TDOA; clock skew; TPSN; Kalman filtering; synchronization precision
0 引 言
基于目標辐射源的无线通信定位系统是由空间独立的信号接收设备(实现三维定位至少需要4台接收设备)、实现定位解算的中心控制系统和实现各接收设备之间通信的无线通信单元。其总体架构如图1所示。为实现移动通信用户的定位,必须实现以下几部分的技术研究:高灵敏度信号接收技术、接收设备之间的高精度同步技术和TDOA(Time Difference of Arrival)位置估计解算技术。基于TDOA的定位精度一方面取决于参考点的位置检测可靠性,另一方面取决于信号到达接收设备时间的测量精度。如果一个基于TDOA的无线定位系统不能实现各个接收设备之间的高精度时间同步,就不可能获得准确的由各接收设备发送的用于TDOA解算的到达时间值,也就不能获得准确的被测目标的位置解算。信号接收设备之间的时间不一致性最终将反映到定位解算方程中的距离测量上。信号接收设备之间的精确时间同步成为基于TDOA定位的核心技术之一,各信号接收设备间的低成本ns级的时间同步是高精度定位的难点之一。
传统的时间同步方法有自由同步和分布式同步两种。自由同步一般采用原子钟,具有高精度、不受干扰的优点,但是设备复杂、价格昂贵。分布式同步又可分为主从同步和转发同步[1]。主从同步是主设备发射信号,从设备收到主设备信号后发射带有接收发射时间信息的信号,采用锁相环等技术,具有一定的抗干扰能力。转发同步是从设备直接转发主设备发射的信号,受传播路径的影响较严重。本文研究的系统采用主从同步方式。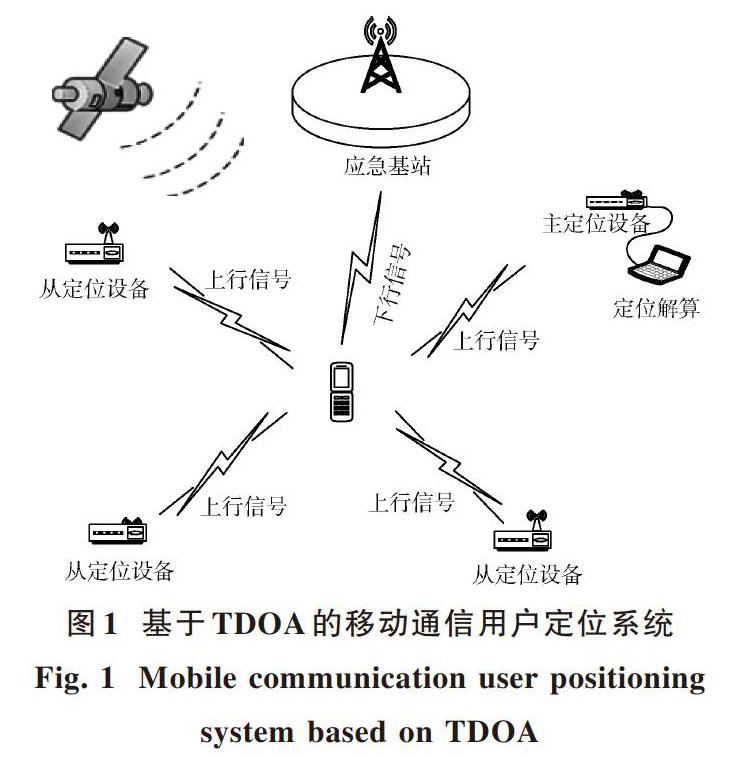
1 相关研究
时间同步的本质是通过牺牲通信带宽和计算功耗来提高时间精度。由于通信带宽产生通信延迟抖动,CPU(Central Processing Unit)处理能力决定时间戳精度,因此,基于时间信息包交换的时间同步精度主要由两个方面决定:有偏差的物理时钟和时间信息交换协议(即时间同步算法)[2?3]。
1.1 无线分布式网络的时间同步
基于有线网络的传统时间同步技术在不改变其低功耗等特征时很难应用到无线网络[4?6]。关于无线通信网络时间同步已有多种协议得到广泛应用,主要可分为以下几类:
1) 基于发送者?接收者的双向同步,典型算法如TPSN(Timing?Sync Protocol for Sensor Networks)算法[2,4,7?8]。
2) 基于发送者?接收者的单向时间同步,如FTSP (Flooding Time Synchronization Protocol)算法[9]和DMTS(Delay Measurement Time Synchronization)时间同步算法[10]。
3) 基于接收者?接收者的同步算法,如RBS(Reference Broadcast Synchronization)算法[2]。但它们未能在能效和精度上进行充分的优化。
对于无线网络环境的时间同步需要考虑如下几个问题:
1) 用于处理无线通信的资源;
2) 无线网络的扩展;
3) 无线网络的时间同步基础设施;
4) 无线网络的节点集合。
1.2 TPSN同步算法
TPSN同步算法属于发送者?接收者同步机制算法[4,8,11]。时间同步从根节点开始,构建分层次等级的网络结构。通过与高一级的节点交换时间戳来检查同步情况,通过计算偏移量和交换延迟矫正倾斜角。其时间同步过程如图2所示。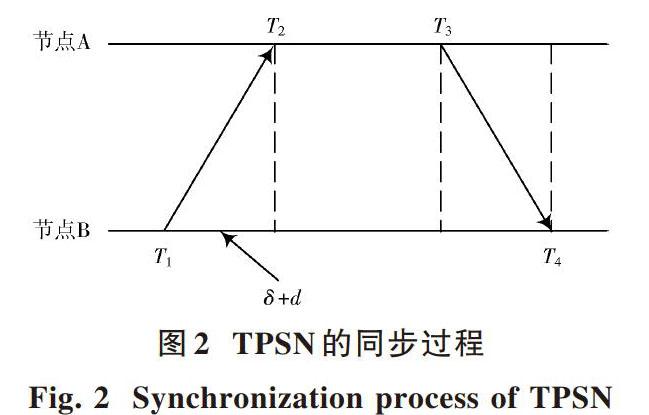
设A为从节点,B为主节点,无线传播时间为[d],两节点时钟的时间偏差为[δ]。同步过程由主节点B在[T1]时刻广播同步开始信息,其包含信息([T1]);从节点A在[T2]时刻接收到同步信息,并记录接收时间[7][T2]:
从式(3),式(4)可以看出,只需一组数据就可以计算出主从节点之间的时间偏差。在传播过程中,如果这组数据信息受到多径延迟或噪声的影响,那么得到的接收时间就有可能不正确,但是通过利用多组数据来计算可以减小数据干扰。
2 时间同步实现
融合北斗与基站的定位采用TDOA定位方法,要求计算被定位终端信号到达各节点的时间差,时间差的准确度取决于各节点之间的同步精度。为使TDOA定位系统中独立节点之间同步误差尽量小,可以利用卫星时钟同步和基于时钟误差矫正的双向数据通信链路达到高精度同步的目的。
2.1 同步系统结构
本文中设定的基于TDOA的移动通信用户定位系统采用主从同步模式[8]。系统结构如图3所示。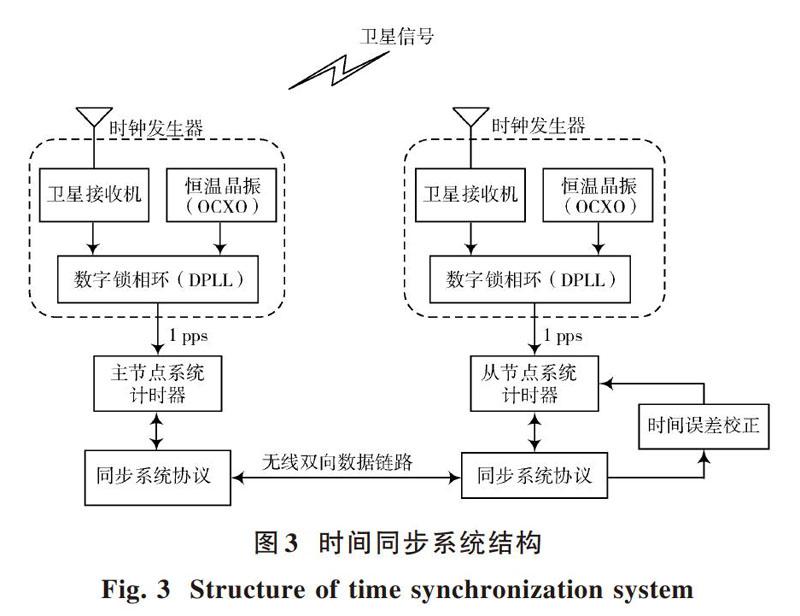
在主、从节点中使用的时钟发生器主要由卫星信号接收机、DPLL(Digital Phase Lock Loop,数字锁相环)、OCXO(Oven?controlled Crystal Oscillator,恒温晶体振荡器)、振荡器漂移补偿算法组成。DPLL用来实现OXCO与卫星接收机提供的1 pps信号的同步,生成具有高频率稳定的系统时钟。然而对于卫星接收机输入DPLL的1 pps信号有短时的抖动,这是由于信号反射、电磁波通过电离层、多径接收等原因产生的。由于通过卫星的原子钟生成的信号具有高稳定性,所以可以通过DPLL环路滤波器的滤波降低抖动。
2.2 双向通信链路
为达到各接收端(节点)之间的精确同步,采用双向通信链路[5,8]。这种方法在两个通信链路上使用时间戳消息,当传送时钟脉冲的路径相同时,在主从节点之间延时是相互抵消的。因此两个接收机之间时钟差的估计是可行的。为了使时间戳信息在双向链路上的传输延时相同,需要将所有的处理都在硬件中实现,从而使时延不会发生改变。最好是让时间戳的生成位置在与传输介质最近的物理层。
当在物理层使用时间戳时,在传输和接收的过程中不确定因素是传播时间。当主从节点之间是视距传播时,则双向传输的电波传播时延差就很小,因此可以准确地估计两个节点之间的时钟差。为此,本文研究的时间同步系统时间戳在物理层生成。无线信号的处理采用SDR(Software Define Radio)实现,CPU使用TI公司的DSP芯片,它结合FPGA实现无线信号的调制解调和处理。以这种方式实现时间戳可以使双向链路的时间延迟最小化。
2.3 时间同步协议和误差矫正
针对一主三从4个终端的TDOA定位系统,设计如图4所示的TPSN同步协议。对TPSN协议做了改进[8,12],对于时间戳的需求数量相对于TPSN大大减少。它可以降低无线数据链路的压力,缩短时间同步实现的时间。
圖4中TPSN协议的运行顺序描述如下:
1) 首先发送用于首次同步的同步广播消息。
2) 各从节点接收到同步信息后,保存[T2]时间信息;每个从节点依次发送同步脉冲消息后,保存[T3]时间信息;在第一阶段没有接收到3个同步脉冲时请求重传。
3) 同步应答消息广播包括时间信息[T1]和[T4]。
4) 在接收到应答消息后,利用[T1],[T2],[T3]和[T4]校正[θ],[θ=(T2-T1)-(T4-T3)2]。
2.4 基于卡尔曼滤波的时钟误差校正
如果获取的时间戳信息是精确可靠的,从节点的本地时钟校正可以直接利用时钟偏移和时钟偏移率实现,从而达到主节点与从节点间的时间同步。在同步协议已建立的前提下,信息包交换过程中还存在测量噪声和传输时延等不确定性因素导致得到的时间信息不精确。所以在这里采用滤波器对其进行预处理。在本文研究的带有时钟偏移的同步系统中,通过卡尔曼滤波器(Kalman Filter,KF)对时钟偏移和偏移率进行估计,实现时间同步误差校正[13?16]。
2.4.1 时钟校正原理和Kalman算法
TPSN算法采用的发送/接收模型如图5所示,针对主节点和其中任何一个从节点运用直接双向同步算法,可以计算从节点的本地时钟的漂移率和时钟偏移。
定义从节点在[t]时刻(主节点时间)的时间为[H(t)],[H(t)]与参考时间[t]的时间偏差为从节点的时钟偏差[θ(t)],定义[t]时刻时钟漂移[α(t)],时钟漂移变化率为[β(t)],其中[α(t)]是[θ(t)]的时间导数,[β(t)]是[α(t)]的时间导数。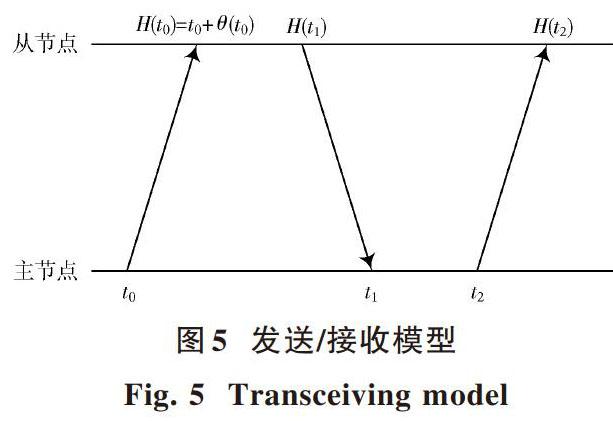
由于晶体振荡器存在老化问题,而且受环境温度的影响,时钟漂移不是恒定不变的。从时钟与主时钟具有非线性关系,在本文中,定义时钟模型[14]如下:
2.4.2 仿真分析
利用Matlab软件进行时钟校正,仿真实验中,主从时钟的工作频率设置为80 MHz,从时钟相对于主时钟的时钟漂移为2[×]10-10 s,时钟漂移率为1[×]10-11 s,同步周期选择1 s,观察卡尔曼滤波前后时间偏差情况,如图6所示。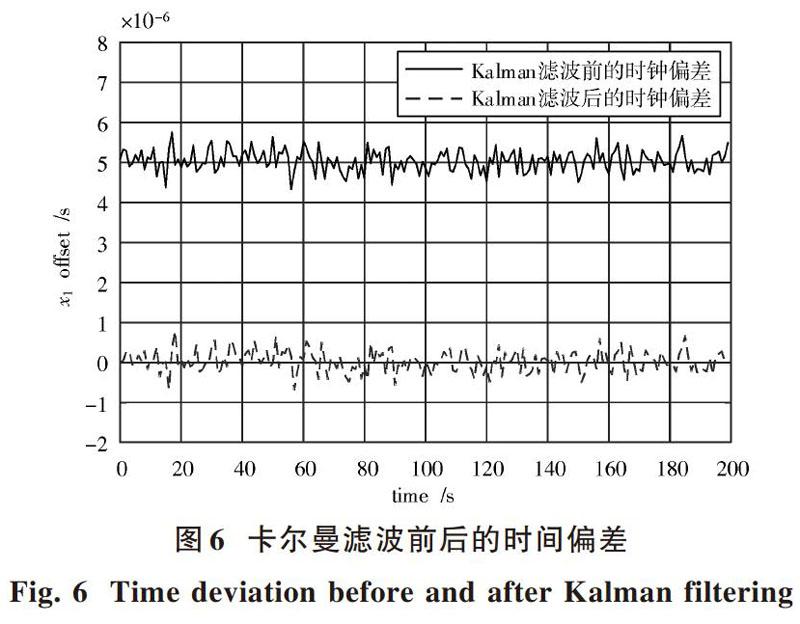
由图6可见,进行卡尔曼滤波前、后时钟偏差是随机变化的,对仿真数据进行统计分析,计算滤波前后的时钟偏差的均值和方差得到的结果如表1所示。
通过卡尔曼滤波估计得到状态的估计值,使从时钟的偏差得到补偿,并对时钟模型进行修正,最终实现从时钟与主时钟的同步。从图6可见卡尔曼滤波算法可以明显减小主从时钟之间的时间偏差。由图7,图8可知,经过卡尔曼滤波后从时钟的漂移情况得到了改善,时钟漂移率随着时间的收敛效果明显。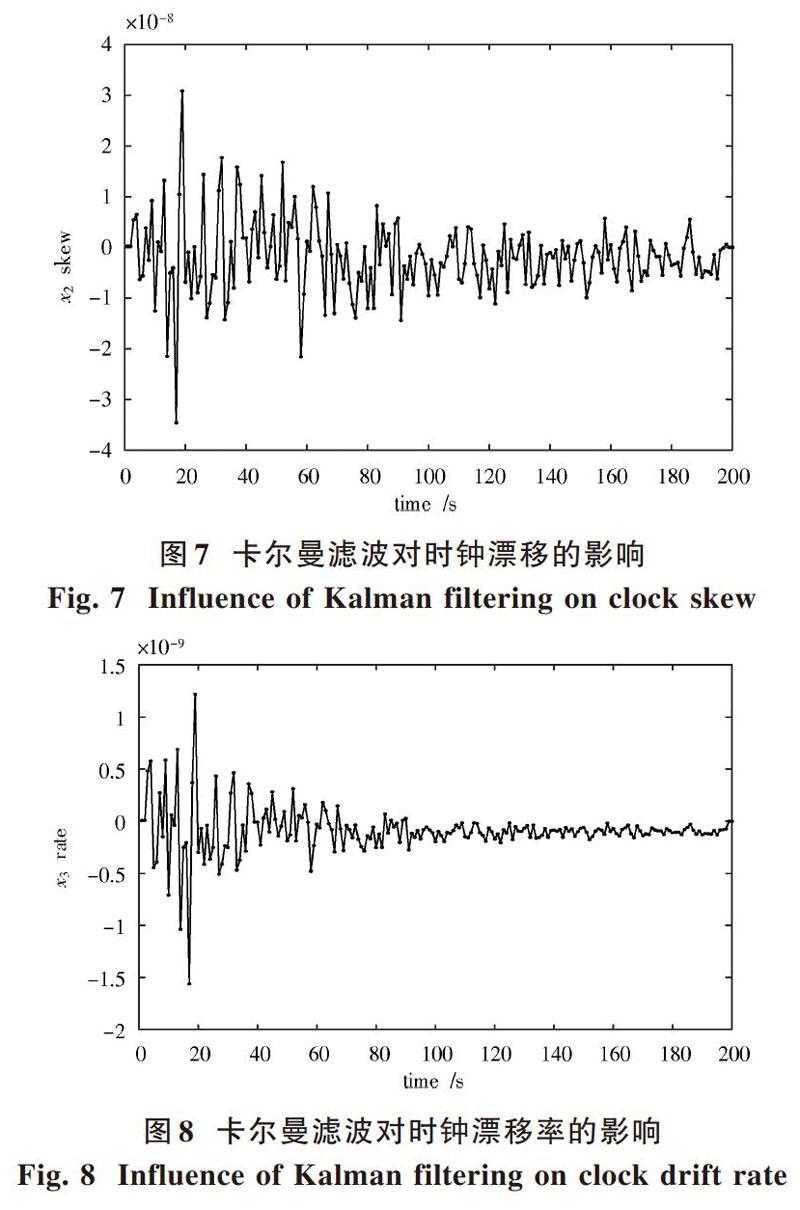
3 结 语
基于TDOA的无线定位系统中,时间同步是整个系统提高定位精度的重要方面,主从同步中的TPSN同步方式一方面可以提高时间精度,另外,还可以降低能量消耗。本文研究的一主三从定位系统采用改进的TPSN方法,对于时间戳的需求数量相对于TPSN大大减少。利用基于卡尔曼滤波的双向同步算法,不仅时钟偏差的测量噪声被有效消除,而且实现了对时钟漂移以及时钟漂移变化率的估计。另外,在对时钟偏差进行补偿的同时,修正从时钟系统时间,从而提高无线定位系统的TDOA定位精度,仿真结果表明,卡尔曼滤波器能明显减小主从时钟的偏差,并且在对时钟偏差进行补偿的同时,修正从时钟系统时间,从而降低无线定位系统的TDOA定位时钟的偏差。
参考文献
[1] MASNE V, BADHIYE S, SAMBHE N, et al. Clock synchroniza?tion in distributed area [J]. International journal of computing and technology 2014, 1(3): 114?120.
[2] 叶玲,李太华,代学武.无线传感器网络环境下基于卡尔曼滤波的PTP协议[J].智能系统学报,2012,7(6):518?524.
YE L, LI T H, DAI X W. Kalman filtering based precision time protocol (PTP) in wireless sensor networks [J]. Transactions on intelligent systems, 2012, 7(6): 518?524.
[3] LIU D, ZHENG Z, YUAN Z, et al. An improved TPSN algorithm for time synchronization in wireless sensor network [C]// 2012 the 32nd International Conference on Distributed Computing Systems Workshops. Macao, China: IEEE, 2012: 279?284.
[4] 陶志勇,胡明.无线传感器网络中基于层次结构的时间同步算法[J].计算机应用,2012,32(6):1513?1515.
TAO Z Y, HU M. Time synchronization algorithm based on hierarchical structure in wireless sensor network [J]. Computer applications, 2012, 32(6): 1513?1515.
[5] IWAMURA M, UCHINO T. Mobile communication method of requesting synchronization [P]. 2015?08?09.
[6] MANITA A. Clock synchronization in symmetric stochastic net?works [J]. Queueing systems, 2014, 76(2): 149?180.
[7] GANERIWAL S, KUMAR R, SRIVASTAVA M B. Timing?sync protocol for sensor networks [C]// 2003 International Conference on Embedded Networked Sensor Systems. [S.l.]: ACM, 2003: 138?149.
[8] YOON J Y, KIM J W, LEE W H, et al. A DoA?based localiza?tion using precise time?synchronization [J]. Animal feed science & technology, 2012, 71(S1/S2): 1266?1271.
[9] ELSON J, GIROD L, ESTRIN D. Fine?grained network time synchronization using reference broadcasts [J]. ACM SIGOPS operating systems review, 2002, 36(1): 147?163.
[10] 康冠林,王福豹,段渭军.无线传感器网络时间同步综述[J].计算机测量与控制,2005,13(10):1021?1023.
KANG G L, WANG F B, DUAN W J. Survey on time synchroni?zation for wireless sensor networks [J]. Computer measurement and control, 2005, 13(10): 1021?1023.
[11] 张白桦.基于TPSN的时间同步改进算法[J].计算机工程,2010,36(9):109?110.
ZHANG B H. Improved tine synchronization algorithm based on TPSN [J]. Computer engineering, 2010, 36(9): 109?110.
[12] GARONE E, GASPARRI A, LAMONACA F. Clock synchroni?zation protocol for wireless sensor networks with bounded communication delays [J]. Automatica, 2015, 59(C): 60?72.
[13] 庄晓燕,王厚军.基于卡尔曼滤波器的IEEE 1588时钟同步算法[J].电子测量与仪器学报,2012,26(9):747?751.
ZHUANG X Y, WANG H J. IEEE 1588 clock synchronization algorithm based on Kalman filter [J]. Journal of electronic measurement and instrument, 2012, 26(9): 747?751.
[14] KIM K S, LEE B G. KALP: a Kalman filter?based adaptive clock method with low?pass prefiltering for packet networks use [J]. IEEE transactions on communications, 2000, 48(7): 1217?1225.
[15] WELCH G, BISHOP G. An introduction to the Kalman filter [J]. Course notes of ACM siggraph, 1995, 8(7): 127?132.
[16] WANG T, GUO D, CAI C Y, et al. Clock synchronization in wireless sensor networks: analysis and design of error precision based on lossy networked control perspective [J]. Mathematical problems in engineering, 2015(2): 1?17.

