基于改进粒子滤波的稀疏子空间单目标跟踪算法
宫海洋 任红格 史涛 李福进
摘 要: 針对单目标跟踪问题,提出基于改进粒子滤波的稀疏子空间单目标跟踪算法。在改进的粒子滤波中提出将样本分为正、负和过渡样本,减小粒子退化带来的影响,通过仿真实验验证改进粒子滤波器可提高目标跟踪的鲁棒性。仿照人眼视觉神经系统,将稀疏子空间引入粒子滤波中,建立一个稀疏最优化模型,获得稀疏矩阵,稀疏子空间有针对性地对目标进行聚类,得到聚类中心位置实现目标跟踪。经过在相同视频序列实验与基本粒子滤波同mean?shift算法目标跟踪的实验对比可知,单目标跟踪的快速性和鲁棒性得到了很大提高。
关键词: 目标跟踪; 贝叶斯滤波; 粒子滤波; 稀疏子空间; 过渡样本; 聚类中心
中图分类号: TN911.1?34; TP18 文献标识码: A 文章编号: 1004?373X(2018)13?0010?04
Abstract: A sparse subspace single target tracking algorithm based on improved particle filtering is proposed for single target tracking problem. On the basis of improved particle filtering, a method to classify the sample into positive, negative and transition samples is proposed to reduce the influence of particle degradation. The simulation experiment results show that the improved particle filter can improve the robustness of target tracking. On the basis of human visual nervous system, the sparse subspace is introduced into the particle filtering, and a sparse optimal model is established to obtain the sparse matrix. The target is clustered in the sparse subspace to get the location of the clustering center and realize the target tracking. The result of same video sequence experiment is compared with those of the target tracking experiments for basic particle filtering algorithm and Mean?shift algorithm. The results indicate that the accuracy and robustness of single target tracking algorithm are greatly improved.
Keywords: target tracking; Bayesian filtering; particle filtering; sparse subspace; transition sample; clustering center
0 引 言
目标跟踪是对视频中所标记的目标实施状态估计的过程,通过对时间和空间相对性的判断,确定跟踪目标在视频序列中每一帧的位置和姿态。2013年,文献[1]提出一种LDSs算法,通过聚类和噪音压制等处理验证了该方法的准确性。2013年,文献[2]提出一种检测人类行为的新方法,结合稀疏的外观特征和运动特征捕捉目标在视频中的微小变化,通过实验表明算法提高了处理数据的快速性。2015年,文献[3]提出一种基于颜色和空间信息的多特征融合目标跟踪算法,通过实验对目标的平均位置误差进行判断,确定提出的算法使得鲁棒性提高。2016年,文献[4]提出LRSP算法,针对目标受光照和姿态变化的影响具有更好的鲁棒性。
针对目标跟踪的鲁棒性和准确性,本文提出基于改进粒子滤波的稀疏子空间单目标跟踪算法,仿照人眼视觉神经系统[5],将高维空间中数据映射成低维子空间数据,通过对映射后的数据聚类和学习分类,采用粒子滤波实现在线跟踪目标。在实验环节,将本文算法与已提出的跟踪方法进行比较,通过定量和定性分析验证算法的有效性。
1 粒子滤波器的改进与稀疏子空间表示
1.1 粒子滤波器的改进
针对粒子退化和多样性匮乏的弊端,本文把粒子集分为三类样本,即正样本、负样本、过渡样本。三类样本分布如图1所示,3个箭头从上至下依次为正样本、过渡样本、负样本。加入过渡样本,使得粒子滤波器偏离真实状态较小的数据保留下来,减少这些数据被丢弃的可能性,进而增加数据的多样性,使得跟踪过程中得到的目标更接近真实目标。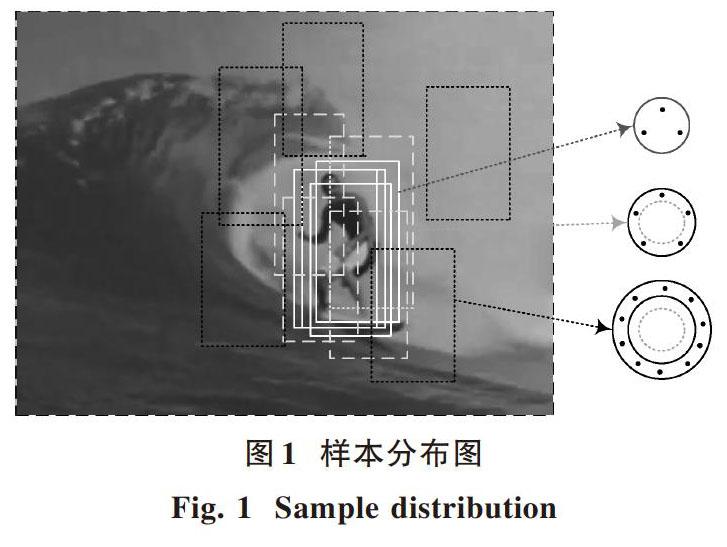
对加入过渡样本的粒子滤波进行实验验证,对100个粒子集组成的空间进行粒子跟踪。图2中实线为粒子实际运动曲线,虚线为基本粒子滤波运动曲线,点线为加入过渡样本的粒子滤波运动曲线。由运动曲线图可知,相对基本粒子滤波,加入过渡样本的粒子滤波运动曲线对粒子追踪更加准确。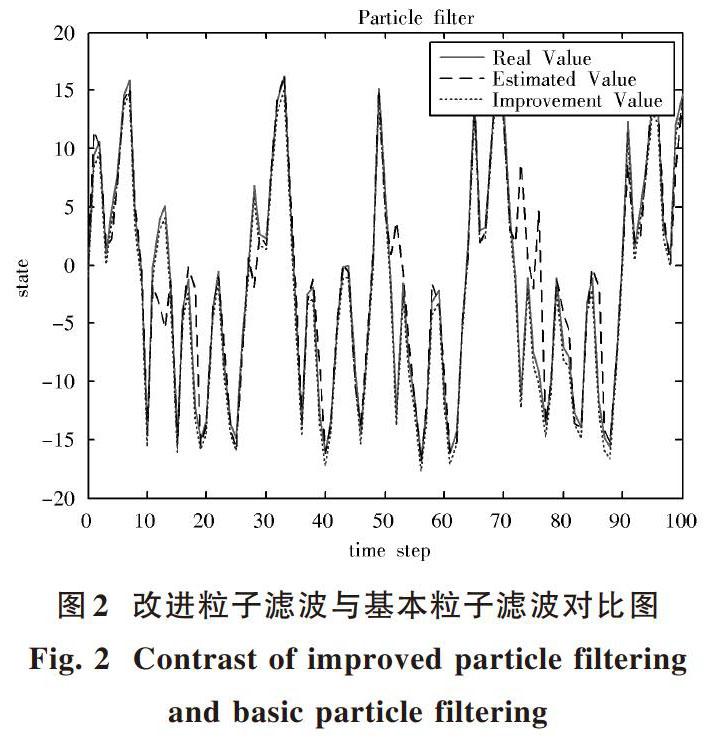
1.2 粒子的稀疏子空间表示
人类视觉的认知能力很强,其注意机制可以在环境恶劣的条件下对目标实现准确识别与跟踪。有研究表明[6?7],人类视觉被生活中的某个物体吸引时,只有神经元中少量的神经元被激活,从而处于活跃状态,而其他的大部分神经元则处于睡眠状态没有被激活。这说明人类视觉在对目标进行观察时用少量的神经元就可以很好地表示目标。稀疏表示正是由人类视觉系统的工作原理启发而提出的,并且在模式识别领域得到相当广泛的应用。
求解稀疏方程的解实际上是一个凸优化的问题,可通过凸松弛算法与贪婪算法计算。在凸松弛算法中,最具代表性的是(Least Absolute Shrinkage and Selection Operator,LASSO)算法[11],该算法计算量较大。在贪婪算法中,使用较多的是(Orthogonal Matching Pursuit,OMP)算法[12]。由于该算法具有收敛速度快的优点,本文使用该算法对稀疏方程进行求解。
2 实验设计和结果分析
2.1 实验设计
具体实验步骤如下所示:
步骤1:初始化,[t=1],在目标位置区域提取正样本,背景区域采样得到负样本,在目标区域与背景区域之间采样得到过渡样本,将三类样本构造成目标样本[Y];
步骤2:由目标位置样本数据构造源数据[X],通过稀疏子空间矩阵[D]的计算可得到与正样本相同样本的聚类;
步骤3:将采集得到的聚类粒子作为改进粒子滤波器的输入,经粒子采样、加权、估计输出,重采样,重复步骤3直到相似度值小于设定阈值。
2.2 实验结果分析
为验证本文提出的基于粒子滤波的稀疏子空间单目标跟踪算法的有效性,实验设计包括目标尺寸变化和短时間目标遮挡下的目标跟踪。将本文的跟踪结果与mean?shift算法和粒子滤波算法进行对比,定性分析跟踪算法的性能,如图3,图4所示。其中,虚线框为本文算法,实线框为粒子滤波算法,点线框为mean?shift算法。
2.2.1 定性分析
实验1:在图3surfer视频序列中,选取人物上半身为跟踪目标,目标初始位置为[x0=](277 135 60 120)。主要特点是场景中目标位置发生变化和旋转并伴有尺度变化,选取视频1~375帧,在目标运动过程中发生尺度变化,影响目标跟踪,实验结果包含视频帧中的第30,70,200,290帧。
实验2:在图4选择的视频序列中,选取人的脸部为跟踪目标,目标初始位置为[x0=](120 55 75 95)。主要特点是随着光照发生变化对目标追踪的影响。选取视频1~350帧,实验结果包含视频帧中的第54,118,246,330帧。根据实验图像显示本文追踪误差小。
2.2.2 定量分析
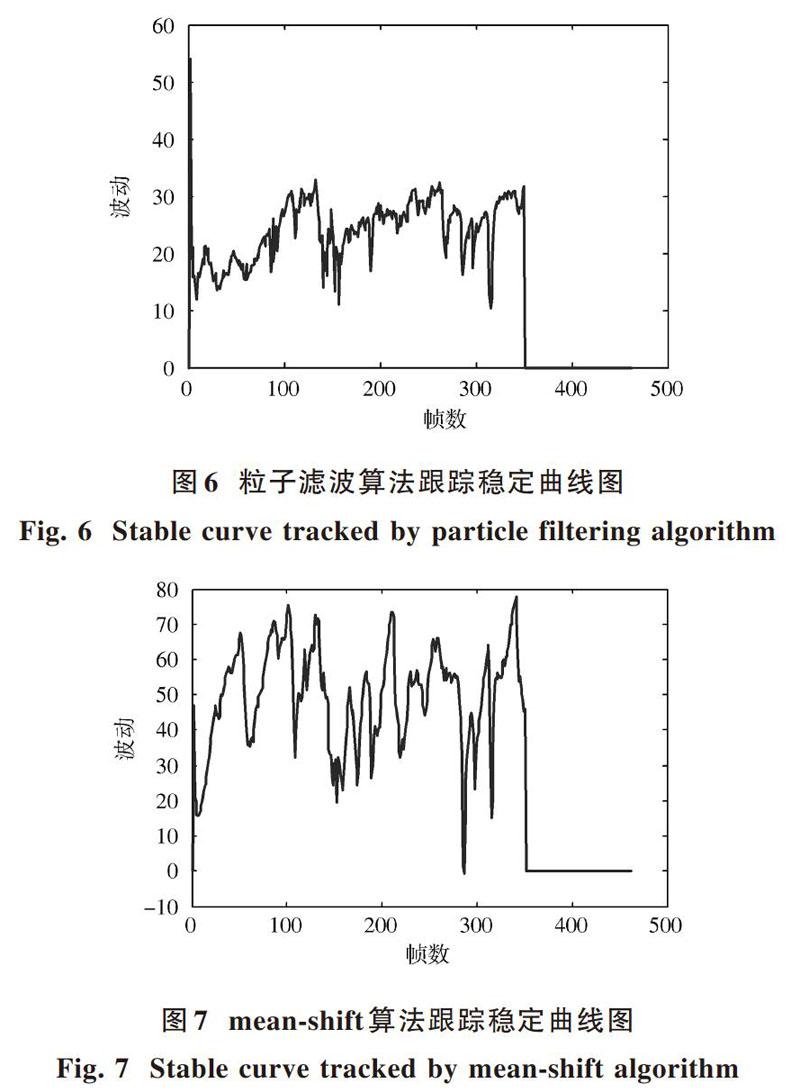
图5~图7分别为本文算法、粒子滤波和mean?shift算法跟踪过程中的稳定曲线。在Matlab中用tic与toc口令计算对同一个视频序列(为节约时间只计算前350帧)进行跟踪的时间,图5用时23.117 2 s,图6用时24.627 3 s,图7用时28.764 4 s。根据实验时间可知,本文算法在时间上得到了提高,由稳定曲线图分析,本文算法相对稳定。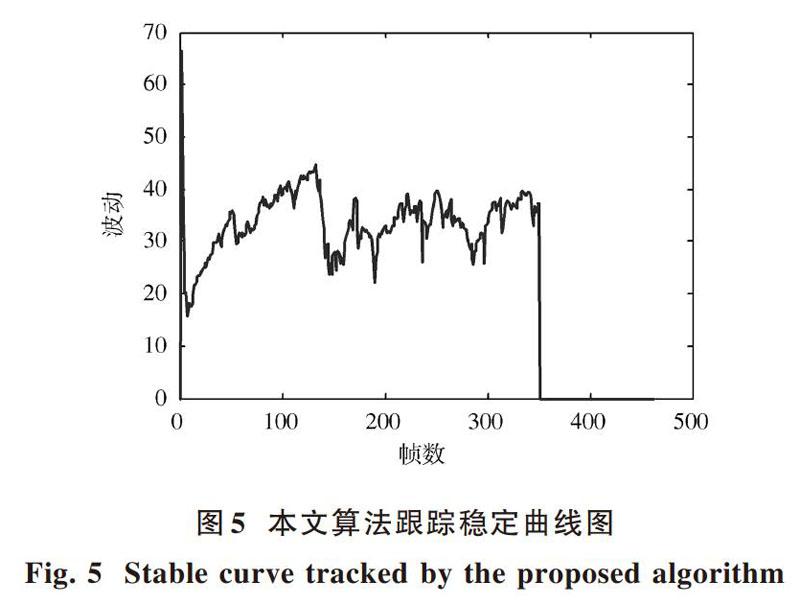
3 结 论
本文通过实验验证改进后的粒子滤波的有效性,将改进的粒子滤波和稀疏子空间理论结合,实现对采样粒子的预处理,减少后面算法的冗余计算,提出基于改进粒子滤波的稀疏子空间单目标跟踪算法。最后由实验结果的定量和定性分析总结可知,本文算法在时间上得到加快,并且对光照变化和尺度变化所带来影响的鲁棒性提高。
参考文献
[1] WANG H, YUAN C, LUO G, et al. Action recognition using linear dynamic systems [J]. Pattern recognition, 2013, 46(6): 1710?1718.
[2] YANG S, YUAN C, WANG H, et al. Combining sparse appearance features and dense motion features via random forest for action detection [C]// 2013 IEEE International Conference on Acoustics. [S.l.]: IEEE, 2013: 2415?2419.
[3] 许婉君,侯志强,余旺盛,等.基于颜色和空间信息的多特征融合目标跟踪算法[J].应用光学,2015,36(5):755?761.
XU Wanjun, HOU Zhiqiang, YU Wangsheng, et al. Multi feature fusion target tracking algorithm based on color and space information [J]. Applied optics, 2015, 36(5): 755?761.
[4] 陈芸,吴飞,荆晓远,等.鲁棒低秩稀疏表示的在线目标跟踪[J].计算机工程与设计,2016,37(4):1062?1066.
CHEN Yun, WU Fei, JING Xiaoyuan, et al. Robust low rank sparse representation for online target tracking [J]. Computer engineering and design, 2016, 37(4): 1062?1066.
[5] 赵二群.视觉神经系统仿生模型及其应用研究[D].长沙:湖南大学,2014.
ZHAO Erqun. Bionic model of visual neural system and its application research [D]. Changsha: Hunan University, 2014.
[6] HINAULT T, DUFAU S, LEMAIRE P. Strategy combination in human cognition: a behavioral and ERP study in arithmetic [J]. Psychonomic bulletin & review, 2015, 22(1): 190?199.
[7] OLSHAUSEN B A, FIELD D J. Natural image statistics and efficient coding [J]. Network, 2009, 7(2): 333.
[8] 周小娟,李春晓.基于偏最小二乘分析和稀疏表示的目标跟踪算法[J].重庆邮电大学学报(自然科学版),2014,26(1):104?110.
ZHOU Xiaojuan, LI Chunxiao. Target tracking algorithm based on partial least squares analysis and sparse representation [J]. Journal of Chongqing University of Posts and Telecommunications (natural science edition), 2014, 26(1): 104?110.
[9] 梁锦锦,吴德.稀疏[L1]范数最小二乘支持向量机[J].计算机工程与设计,2014,35(1):293?296.
LIANG Jinjin, WU De. Sparse [L1] norm least squares support vector machine [J]. Computer engineering and design, 2014, 35(1): 293?296.
[10] CHEN Guoxin, CHEN Shengchang, WANG Hanchuang, et al. Sparse reconfiguration of geophysical data based on L0 norm minimization [J]. Applied geophysics, 2013, 10(2): 181?190.
[11] BAI T, LI Y F. Robust visual tracking with structured sparse representation appearance model [J]. Pattern recognition, 2012, 45(6): 2390?2404.
[12] TIBSHIRANI R. Regression shrinkage and selection via the Lasso [J]. Journal of the royal statistical society, 2011, 73(3): 273?282.

