基于矩阵空域滤波的窄带MUSIC算法研究与应用

景杨王立婷胡银丰

(1.第七一五研究所，杭州，310023；2.海军驻杭州地区军事代表室，杭州，310023)

目标方位估计被广泛的应用于声呐、雷达等领域，由于“瑞利准则”的限制，常规方位估计的方法方位分辨力有限，为了克服这个缺陷，近些年来学者们广泛开展了高分辨方位估计算法的研究，涌现了很多算法，其中比较突出的是MUSIC(multiple signal classification)[1]算法。但是经典MUSIC算法稳健性低且方位分辨信噪比门限较高。为了改善这些缺陷，波束域和矩阵空域滤波预处理方法受到了学者们的广泛关注。Vaccaro[2]等人提出了矩阵空域滤波的方法，MacInnes采用最小均方准则设计矩阵空域滤波器[3]，该方法虽然计算量小，但是稳健性差。国内已经有学者采用二阶锥规划将矩阵空域滤波应用到匹配场空间干扰抑制[4-6]，提高了滤波器输出的稳健性。矩阵空域滤波后不会改变数据的特性，同时能够过滤掉不需要的方位信号，改善后续算法处理的性能。本文研究基于矩阵空域滤波窄带MUSIC方法。

1 矩阵空域滤波器原理与设计

1.1 原理

阵列的接收数据x经过空域滤波器矩阵G（M×M）后的数据y表示如下：

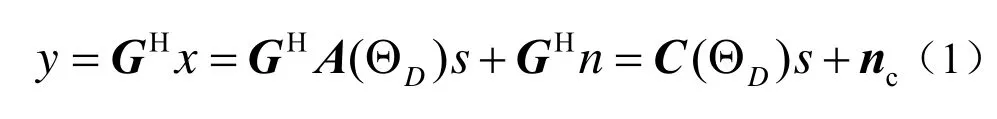
空域滤波器的作用是使通带内的信号通过，使阻带内的信号得到抑制，所以空域滤波器的响应表示为：

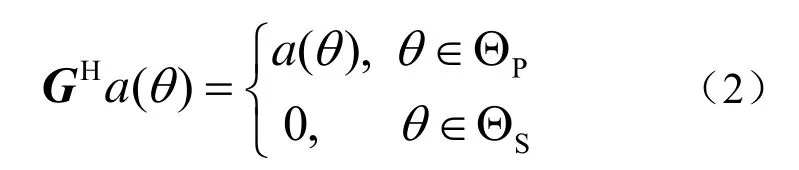
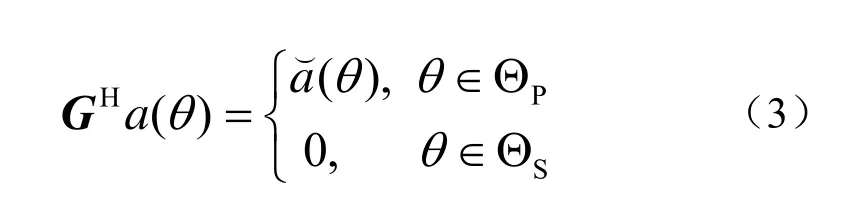
该种情况下矩阵G的维数变成了表示一般情况下设计的虚拟维数，虚拟阵列流形的维数也变成了特别注意的是此时的并不一定等于M，所以式（2）是（3）的特例的一种。

1.2 设计方法

最小均方准则和阻带约束通带最小均方准则常用来设计空域滤波器，下面对两种准则的设计方法进行解释。首先根据设计需要对阻带和通带空间范围进行数学离散化处理，表示阻带空间范围离散化的方位点，表示通带空间范围离散化的方位点。

1.2.1 采用最小均方准则

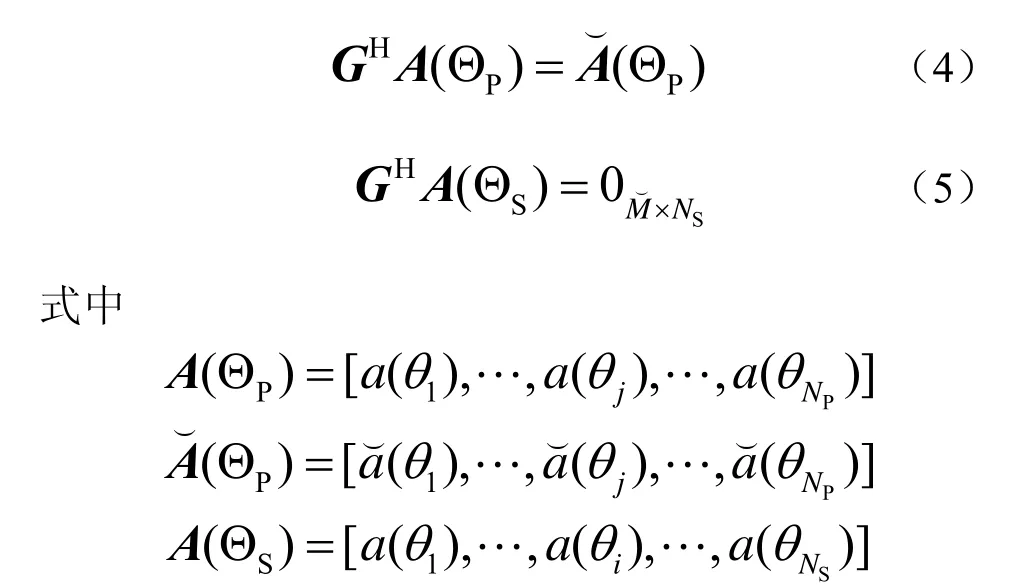
将式（3）改写如下表达式将式（4）和式（5）合成一个表达式为

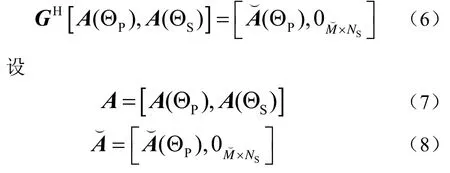
所以式（6）写成矩阵向量表达式为

运用最小均方准则求解G矩阵表达如下式

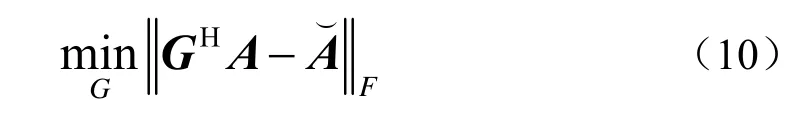
求解得到G矩阵的表达式如下

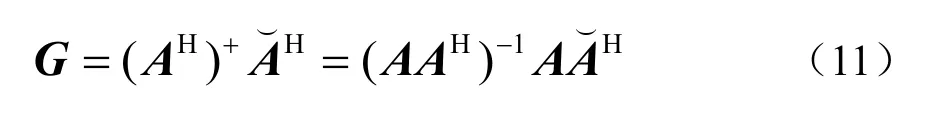
1.2.2 阻带约束通带最小均方准则

滤波器G矩阵的求解问题运用这个准则表达如下：

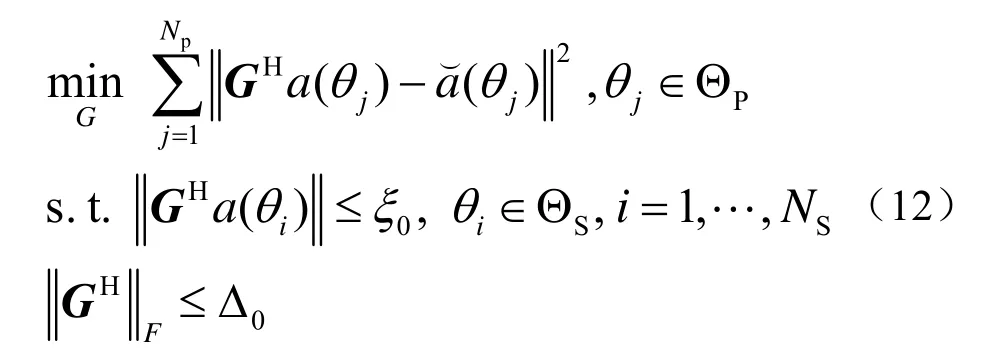
为了求解方便，上面表达式问题可以转化变成二阶锥规划问题，具体操作如下：

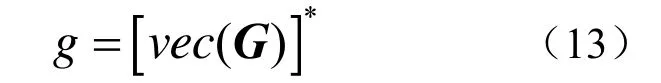
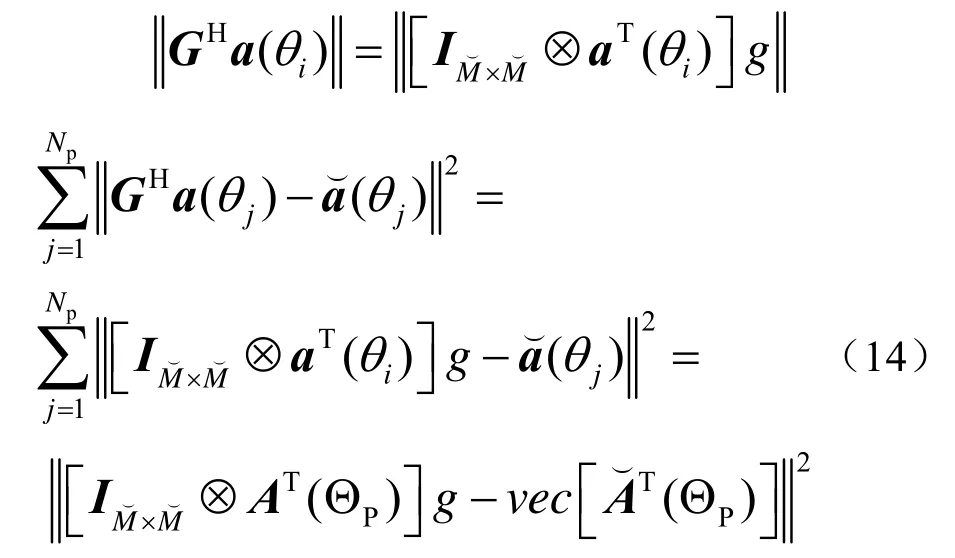
式（12）问题就可以转换成

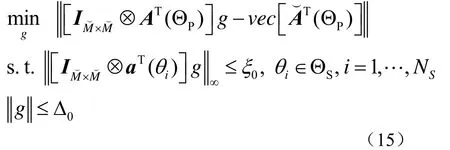
2 本文算法

综上，数据协方差矩阵通过空域滤波后为

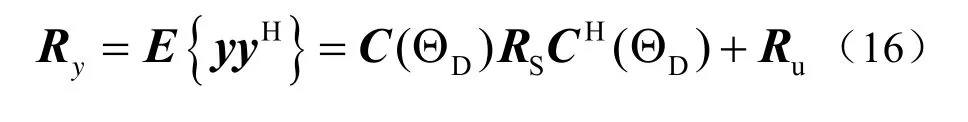
由于设计出的通带响应与期望的响应肯定存在误差，会使过滤波器后的阵列流形发生畸变，为了避免这种情况，改进MUSIC算法的谱峰搜索公式，得到基于空域滤波的MUSIC算法公式

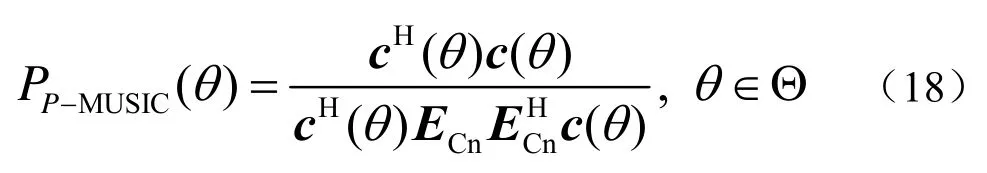
总结以上原理，窄带空域滤波MUSIC算法实现流程如下所述：

1、根据设计需求选择通带空间范围以及阻带空间范围；

2、根据使用目的，选择符合的空域滤波器设计准则；

5、将噪声子空间ECn带入式（17）进行谱峰搜索；

6、与谱峰搜索最大值点相关的角度记为信号的估计方位。

3 性能仿真

3.1 矩阵滤波器响应设计

针对一个半波长均匀间隔的直线阵，阵元数20，其中波长对应频率f0=1 000 Hz，采用最小均方误差和阻带约束通带最小均方准则设计滤波器，同时设滤波器通带的期望响应与实际响应相等两种准则的通带空间范围都设为[−30:1:−10]，前者阻带空间范围取[−90:1:−31]∪[−9:1:90]，后者的阻带空间范围取[−90:1:−33]∪[−7:1:90]。阻带空间范围的衰减定为−25 dB，空域滤波器矩阵的 2-范数约束根据实际测试结果设为 1.7较好，它们的滤波器幅度响应）见图1。

由图1可知，两个准则在通带的响应类似，但是在过渡带和阻带不一样，利用最小均方准则设计过渡带较宽阻带抑制越来越强，而利用阻带约束通带最小均方准则的阻带衰减被准确控制在−25 dB，同时过渡带非常窄。所以在对阻带衰减和过渡带没有特殊要求的条件下，采用两种准则设计滤波器都可以。如果希望阻带衰减到固定分贝数和过渡带较窄时，应考虑使用阻带约束通带最小均方准则设计矩阵空域滤波器。空域滤波器矩阵的2-范数约束的值设置应当保证阻带区域达到设定的衰减量，而通带响应向量的畸变较小，需要根据实际的滤波器参数进行调整。

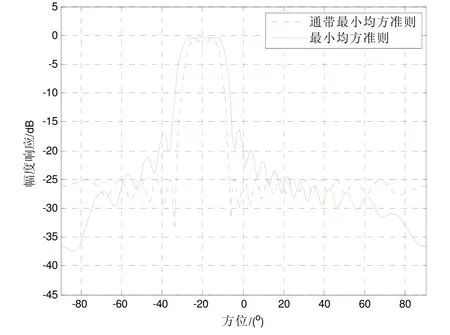
图1 空域滤波器幅度响应

3.2 基于矩阵空域滤波的MUSIC算法性能分析

针对一个半波长均匀间隔的直线阵，阵元数12，其中波长对应频率f0=1 000 Hz，声速c=1 500 m/s，两非相干CW信号从−1°和1°入射，背景噪声为高斯白噪声，采样率fs=5 000 Hz，信号快拍数长度取50，采用阻带约束通带最小均方准则设计滤波器，并假设期望的阵元数等于实际阵元数，通带空间范围设为[−15:0.5:15]，阻带空间范围为[−90:0.5:−22]∪[22:0.5:90]。阻带空间范围衰减为−20 dB，滤波矩阵的2-范数约束根据实际测试结果取1.7较好，设计出的空域滤波器幅度响应如图2，再将经典MUSIC算法和预滤波MUSIC算法对比，对两种算法的分辨概率（当估计的两个信号的波达角满足则表示分辨成功一次，成功次数除以总实验次数得出的结果，式中两信号的估计值，θ1、θ2为真实值）在不同信噪比下[−5:2.5:20]的性能进行分析，独立试验200次，取信噪比为0 dB的一次实验结果见图3，分辨概率性能结果见图4。

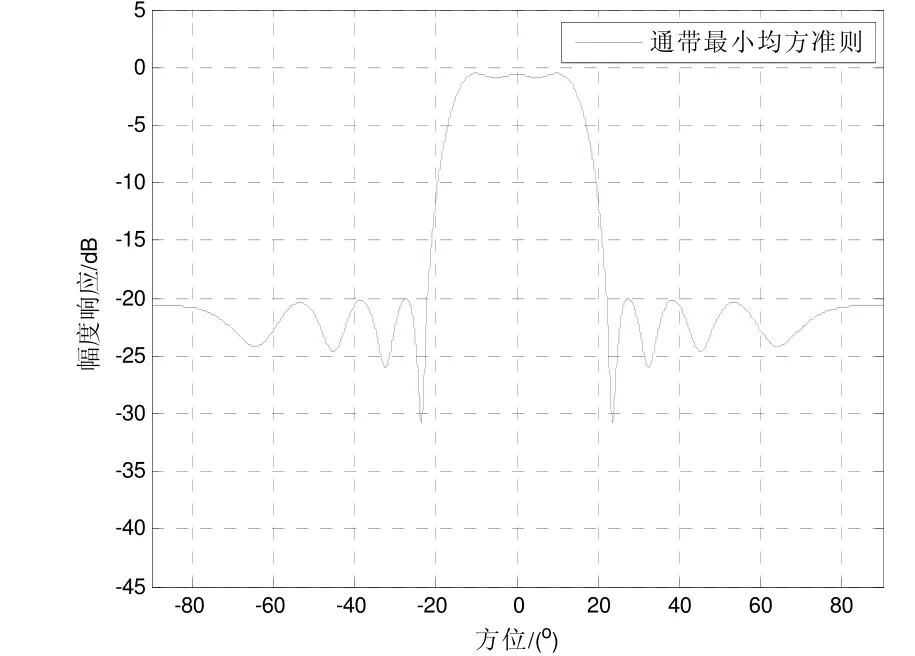
图2 阻带约束通带最小均方准则滤波器幅度响应

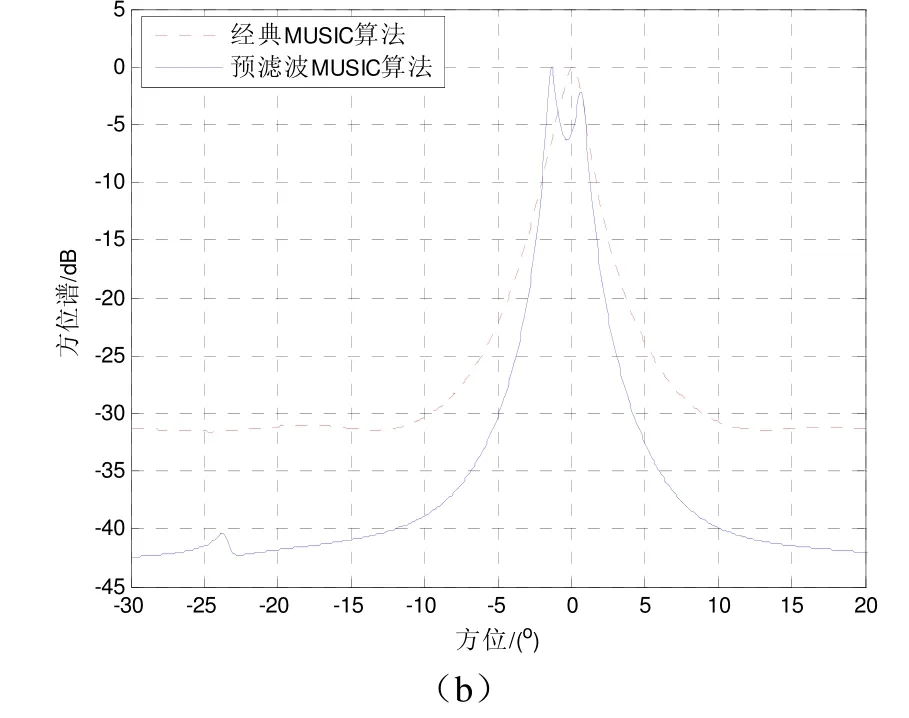
图3 信噪比为0 dB时空域滤波MUSIC算法与经典MUSIC算法方位谱估计

图4 空域滤波MUSIC算法与经典MUSIC算法方位分辨概率随信噪比变化

由图3可知，在较低信噪比和两个目标间隔2°的情况下，经典MUSIC算法已经无法分辨出两个方位的信号，而经过空域滤波的MUSIC算法仍能分辨出两个目标方位，同时由图4知道空域滤波的MUSIC算法具备更高的目标方位分辨力。

4 结束语

本文进行了基于矩阵空域滤波预处理的窄带MUSIC算法波达角方位估计仿真技术研究。经过预处理的 MUSIC算法一定程度上提高了目标方位分辨力。由于时间和条件有限，本文只局限于理论仿真而且对范数约束条件的设置研究不够深入，所以对范数约束条件的研究、海试数据验证和工程实践应用将是下一步研究工作的重点。