溢流式开缝圆管换能器声顺管研究
胡万辉 王力 辛凤歌 薛彬彬
(中船重工海声科技有限公司,宜昌,443000)
开缝圆管换能器是一种理想的小尺寸、低频甚低频、大功率发射换能器,作为低频发射换能器的研究目前在国内处于起步阶段,但在国外很早就有报道。最初出自1957年W T Harris的发明专利[1],1987年H W Kompanek提出了换能器改进方法并将其用于石油勘探[2],2013年B Aronov提出了开缝圆管的解析模型,确定了开缝圆管换能器的振形方程、等效电路模型参数及有效机电耦合系数[3]。这些换能器都是以空气作为背衬,内腔完全密封,由于空腔的存在使得换能器的耐压有限。若采用溢流结构,使内腔与外界流体相通,耐压就非常大,但这种工作方式声辐射效率较低。
国内顺性管作为换能器声顺的研究报道极少,有少量对顺性管结构的椭圆壳体的屈服压力、固有频率或声辐射的理论研究[4-6]。国外顺性管作为换能器声顺的研究有少量公开的文章。N D Miller等人[7]指出高张力钢管制作成横截面为椭圆形时,在静水压超过钢管的屈服张力条件下,能作为低频大功率水声发射换能器的声顺材料,可压缩性在到达材料屈服压力之前能保持恒定。其研究中使用的 4130钢最大工作深度600 m,所设计的声顺管与常规空气声顺管相比能使换能器性能基本不变。W J Tolis等人[8]也提出顺性管能改变小液腔内液体的刚度,这种作用部分是由于顺性管增加了可压缩性,部分是由于顺性管的体积共振。这种顺性管能提供较理想的声顺作用,同时共振频率调节范围宽,在达到屈服强度极限之前,顺性管-液体混合物能使换能器内部产生线性均匀的声压力释放。W J Shashaty[9]研究了扁平圆柱形水声顺性元件的弹性问题后指出,充气型密封管通常用于充油水声换能器以增加内充油的声顺性,在设计顺性管时需要考虑压缩性、屈服压力和顺性管扁平面贴合压力等三个重要特征,制作的声顺管有效工作深度可达310 m。
本文认为使用声顺管可增加溢流流体的有效压缩性,减少内腔流体的声速,进而提高溢流式开缝圆管换能器的声辐射。基于工程实际需要,研究工作频率在100~1 000 Hz的声顺管并进行试验。
1 模型建立及仿真分析
1.1 模型建立
1.1.1 模型特征分析及假设
将B Aronov[3]提出的等效电路模型作为基础模型,该模型没有考虑溢流和声顺的影响,需要改进。由于换能器工作频率低,声波波长远大于开缝圆管及声顺管的尺寸,可以将内部水层和声顺管作为等效流体,并假设它和外部水能完全传递能量。此外,开缝圆管对称面XOY为理想的无限刚性障板,只需对XOY面以上部分建模,通过调整等效流体参数就可以改变开缝圆管发射响应,如图1。
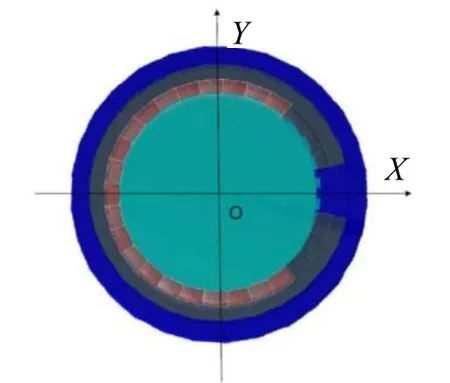
图1 开缝圆管换能器理论模型
1.1.2 换能器模型
溢流式开缝圆管换能器等效电路模型如图 2。换能器内腔包含液体和声顺管,将其看作均匀的流体,其顺性为C,将其定义为空气顺性的x倍:
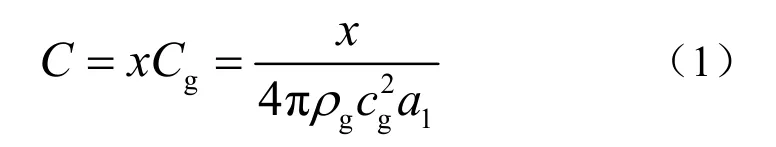
式中Cg为空气柔顺性,ρg和cg分别为内腔空气的密度和声速,a1为开缝圆管内腔半径,模型中其它参数可参考文献[3]。
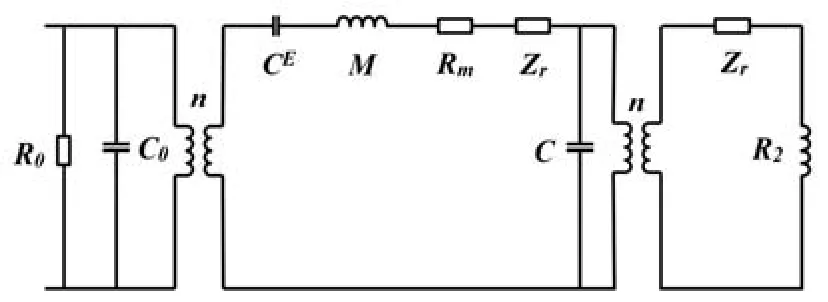
图2 溢流式开缝圆管换能器等效电路模型
1.1.3 声顺管模型
声顺管是由若干个椭圆管均匀分布组成的圆柱体结构,椭圆管沿周向分布示意见图3。
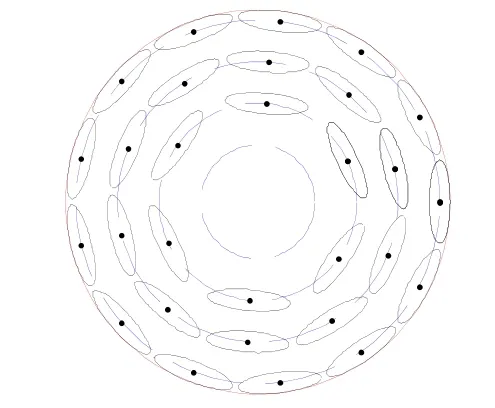
图3 声顺管示意图
这种分布方式可通过下式表示:
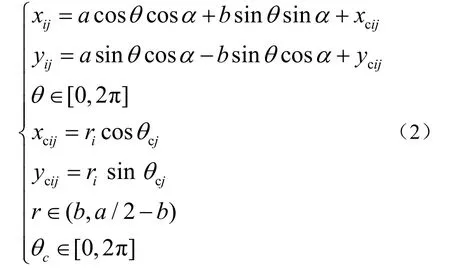
式中,xij、yij分别为椭圆管横截面的横、纵坐标,xcij、ycij为椭圆管中心位置坐标(i、j=1,2,3...n),a、b分别表示椭圆管横截面长半轴和短半轴的长度。
声顺管柔顺性计算表达式为[9]
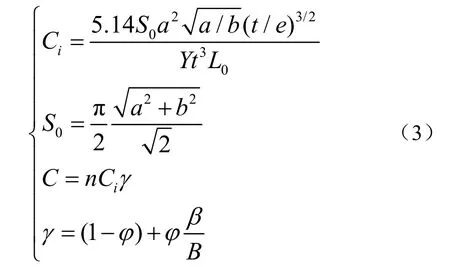
式中,Ci为单个声顺管柔顺性,S0、t、L0分别为椭圆管横截面积、壁厚和长度,Y为材料杨氏模量,γ为顺性调节因子,φ为顺性管占空腔的体积比例系数,β为内腔液体的体积模量,B为椭圆管内空气的体积模量。
1.2 仿真分析
模型求解思路为:首先对换能器模型进行仿真确定x的可行解,确定声顺管应当具有的顺性,在该顺性范围内对声顺管模型进行仿真确定椭圆管几何尺寸及数目的可行解,从中找出最优解,最后对最优解通过有限元方法进行结构力学分析。
1.2.1 换能器模型仿真分析
通过电路仿真,解得换能器发射电压响应、频率和顺性响应关系如图 4所示。从图 4(a)中可看出,当x在0.35~1范围内,换能器的发射电压响应级在100~1 000 Hz频段内均大于120 dB,将此范围作为可行解 I。从图 4(b)中可看出,当x<0.35时,声顺管在频段内共振,导致换能器发射响应出现凹坑。凹坑随顺性减小向高频方向移动,x在0.2到0.35范围内时,凹坑出现在200 Hz以下,在200~1 000 Hz的频段内响应大于120 dB,为了避免声顺结构顺性无法达到可行解I的要求,将此范围也作为可行解II。声顺管应当具有的顺性计算如表1。
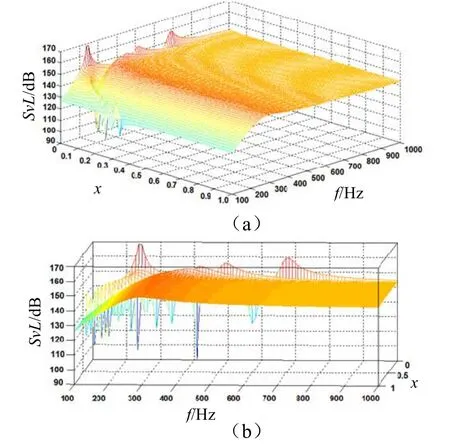
图4 溢流式开缝圆管换能器发射响应、频率和顺性响应仿真结果
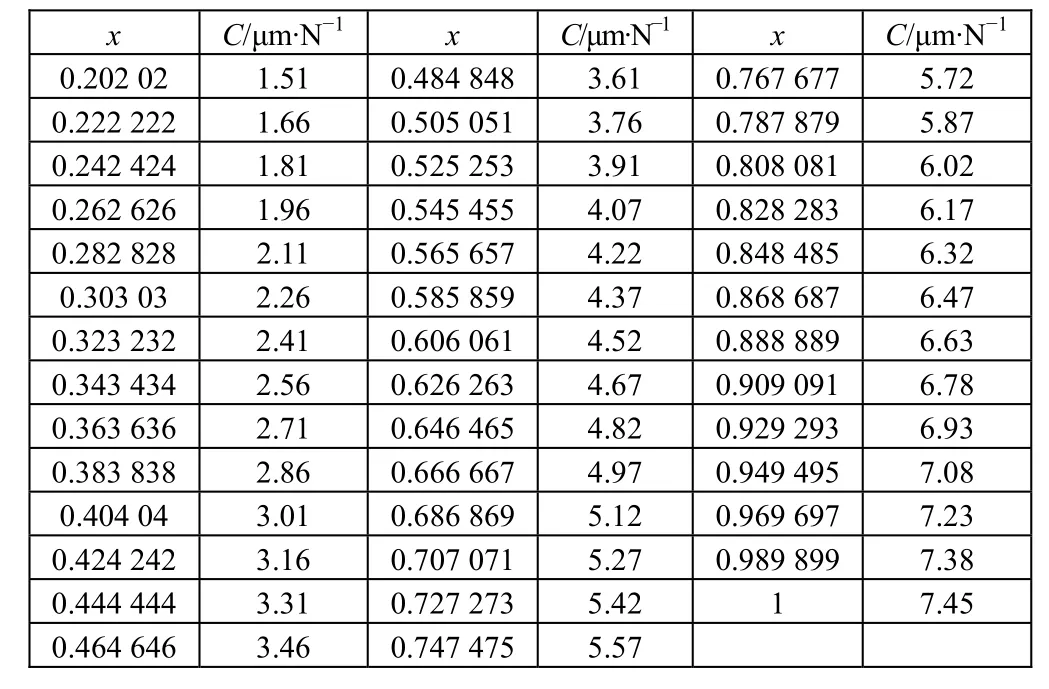
表1 顺性计算表
1.2.2 声顺管模型仿真分析
壁厚1 mm声顺管顺性仿真结果如图5所示,当管直径Φ>45 mm且扁平度a/b>5时,声顺管顺性符合换能器模型的可行解,因此该范围可作为声顺管模型的可行解。
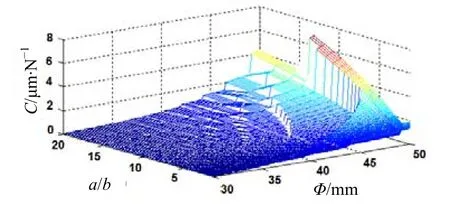
图5 声顺管顺性和扁平度仿真结果
常用不锈钢管尺寸满足要求的有外径 50.8 mm、52 mm和53 mm,其顺性计算结果分别如图6(a)~(c)。从图中可看出三种声顺管共振频率均大于1 000 Hz,椭圆管数目均为n=5个,但顺性不同。三种声顺管最优解分别为Φ=50.8 mm,a/b=13,C=7 μm·N−1;Φ=52 mm,a/b=14.5,C=8 μm·N−1;Φ=53 mm,a/b=17,C=9 μm·N−1。
同理对0.5 mm椭圆管计算得到两组最优解,椭圆管数目均为9个,Φ=45 mm,a/b=17.07,C=7 μm·N−1和Φ=48 mm,a/b=15,C=8 μm·N−1。两种排布结构形式见图7。
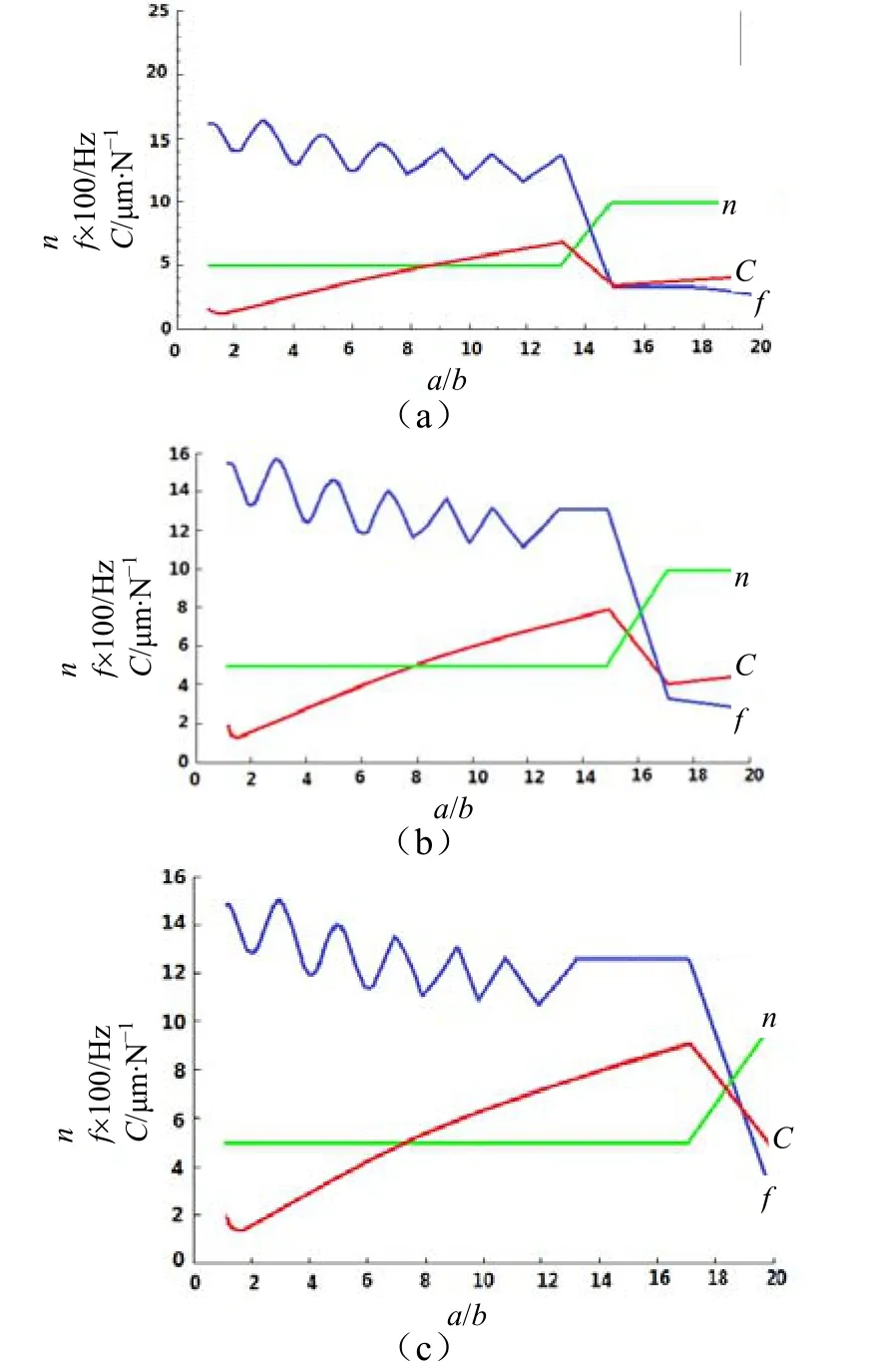
图6 声顺管顺性计算结果
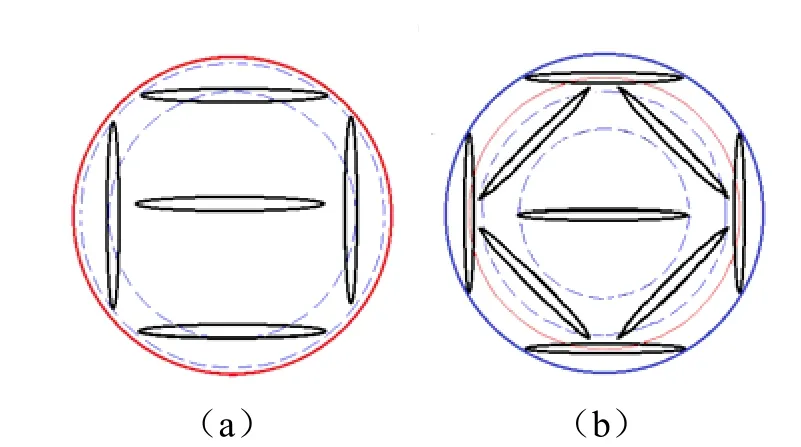
图7 声顺管的排布结构
1.3 结构应力分析
1.3.1 椭圆管耐压分析
在无压力补偿情况下,对上述5种最优解单个椭圆管的耐压进行分析[9],计算结果如表2所示。可以看出,上述椭圆管虽然声性能满足要求,但耐压较低。比较a3和b1,二者扁平度相同,b1厚度是a3的两倍,耐压则是三倍;再比较b1和b2,当壁厚一定且扁平度在同一数量级时,耐压差异较小。因此,提高耐压可优先考虑调节椭圆管的壁厚,但壁厚调节应当兼顾顺性和屈服应力两个因素,将式(3)变形可得到顺性与壁厚的关系为
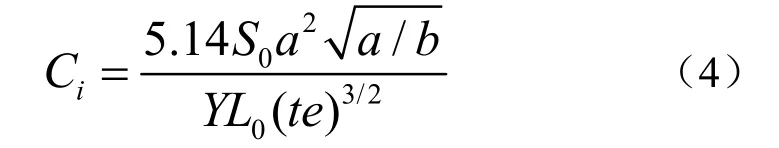
最大应力分布与壁厚关系式为[9]
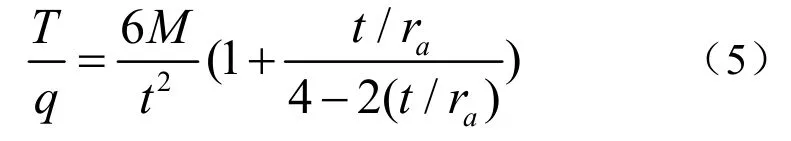
式中M和ra分别表示转动力矩和平均半径,均与壁厚无关。从式(4)、(5)可看出,Ci与管长度L0和壁厚t有关,但T/q只与t有关。因此在调节壁厚的同时,改变管长度可以保持顺性基本不变。
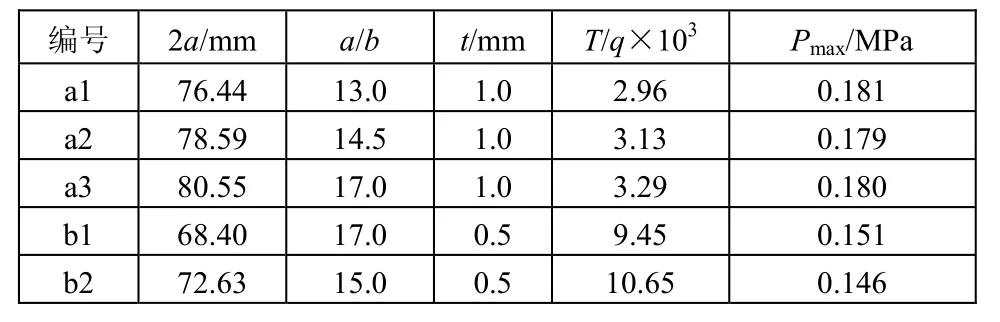
表2 单个椭圆管能承受的最大静压力
1.3.2 声顺管结构应力分布
使用有限元方法计算上述两种排布结构的应力分布,如图8所示,由于椭圆管壁厚较小且无内压补偿,最大耐压约0.2 MPa,若是将厚度提高到3 mm,则耐压可达到3~4 MPa。
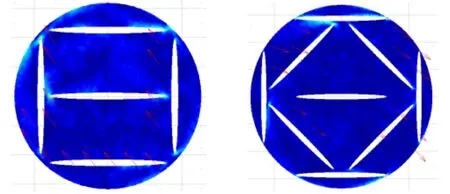
图8 声顺管结构应力分布
1.4 压缩比分析
声顺管的压缩比可由式(6)~(9)计算[9],结果如表3。
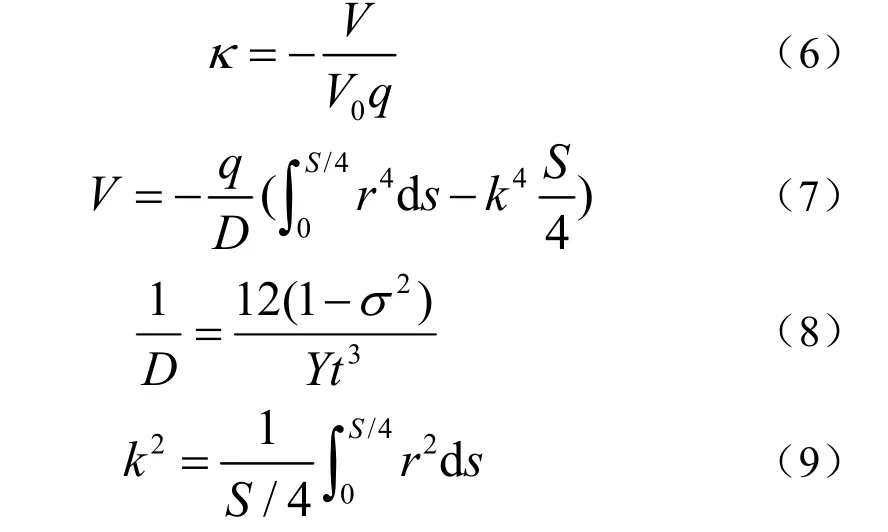
式中,κ为压缩比,V为管单位长度上的体积增量,V0为初始状态管单位长度上的体积增量,q为外压减去内压的差值,D为弯曲刚性,r为椭圆上的点到坐标原点O的距离,S为弧长,S/4为椭圆周长的四分之一,Y和σ分别为杨氏模量和泊松比,k为回旋半径。
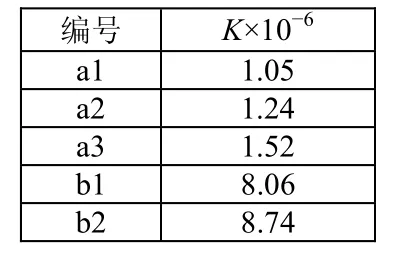
表3 声顺管的压缩比
2 声顺管的制作及测量
2.1 声顺管的设计及制作
根据以上分析,制作压缩比最大的 b2号结构声顺管。首先采用不锈钢椭圆芯棒(2a=72.0 mm,2b=4.8 mm,L0=90.0 mm),对直径Φ=48.0 mm,厚度t=0.5 mm的不锈钢圆管进行冷挤压加工9个椭圆管(2a=75.0 mm,2b=5.0 mm,L0=82.0 mm)。其次用定位夹具将椭圆管定位在支撑底板上,浇注约8 mm厚高温环氧胶,待固化后,采用相同的方法固定上支撑板。另外,为了减小椭圆管对声波的反射,在最外层椭圆管的外表面粘接一层带梯形槽的吸声橡胶,如图9。

图9 声顺管设计图及实物图
2.2 测试及结果
将声顺管安装上开缝圆管换能器,放入水下10 m深,根据国标GB/T 7965-2002《声学 水声换能器测量》方法测量换能器的发射电压响应级和电导,结果如图10。
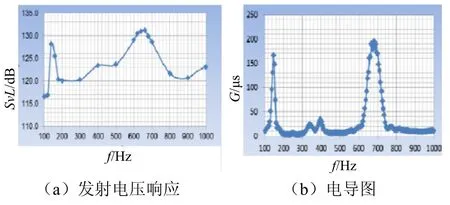
图10 测量结果
测试结果总体与仿真情况接近,在谐振频率660 Hz处发射电压响应级达到131 dB,在130~1 000 Hz都大于120 dB,130 Hz以下在116 dB左右。整个频段内发射电压响应级比仿真结果低,这可能与仿真时换能器内腔是作为一个整体的等效流体,而实际中存在多个金属椭圆管空气腔及部分流体的差异有关。
3 结论
通过对开缝圆管换能器及声顺管的模型建立、仿真及测试结果的分析,可以看出:声顺管的应用可以提高开缝圆管换能器溢流式工作的发射响应,整个频段内试验结果与仿真比较接近;声顺管的设计要考虑不同排布结构、扁平比、厚度对其顺性与耐压的影响。

