基于p-n结中反常光电转换现象的新型带间跃迁量子阱红外探测器∗

刘洁2)# 王禄# 孙令2) 王文奇2) 吴海燕2) 江洋 马紫光王文新 贾海强 陈弘†

1)(中国科学院物理研究所,清洁能源重点实验室,北京 100190)

2)(中国科学院大学,北京 100049)

(2018年4月3日收到;2018年5月3日收到修改稿)

1 引 言

半导体材料中的光电转换过程是光电探测器和太阳能器件的基础,也一直是半导体材料科学和物理学领域的研究热点[1−3].包括太阳能电池和光伏型光子探测器在内的大部分光伏器件都是利用p-n结的光伏效应来实现光电转换的,这被广泛应用在Si基太阳能电池、氮化物太阳能电池、GaAs基太阳能电池和光电探测器,以及CdTe薄膜太阳能电池,InAsSb、HgCdTe和InAs/GaSb超晶格红外探测器等[4−8].

对于太阳能电池和光伏型探测器而言,大的吸收系数和高效的载流子抽取能力对于获得高性能至关重要[9,10].为了充分吸收光能,太阳能电池和光电二极管探测器通常需要利用较厚的体材料[11].但是厚的异质外延层不仅会增加成本,同时由于在失配外延过程中产生位错等缺陷,引入非辐射复合中心,影响了器件的光电效率.这显著降低了利用半导体材料进行光电转换的能力.为了拓展光谱范围,很多研究者开始将低维半导体材料应用于太阳能电池和光伏型探测器[12].

低维半导体材料因具有优异的物理特性,此前一直被广泛应用于电-光转换器件中,例如发光二极管和激光器.在光-电转换器件中,由于其厚度相对较薄,可实现应变外延,因此在光谱范围拓展这一问题上具有一定优势.但由于量子限制效应的存在,如量子阱等低维材料很难应用于利用带间跃迁的光-电转换器件上.这是因为传统半导体物理理论认为[11,13],在低维半导体材料中,光生载流子在形成后会弛豫到基态,由于受到量子限制效应,光生载流子难以逃离限制势垒形成有效的光电流.此外,低维半导体材料的厚度一般较薄,利用有限厚度的低维半导体材料实现光吸收也是难题.因此,传统理论认为将低维半导体材料应用于光伏型探测器领域难以成功.然而,最近发现InAs/GaSb二类超晶格是一种很有竞争性的材料体系,但其暗电流仍然较高,需要制冷系统来实现较好的性能.

对于光电探测器而言,工作波长和暗电流是两个衡量探测器工作水平的重要参数,它们在器件结构设计上很难达到平衡,尤其是对工作在红外波段的探测器更是如此[14,15].探测器的工作波长决定于吸收区材料的带隙,为了探测红外信号,吸收层材料的带隙应较窄.但是窄带隙的材料会带来较大的热载流子生成,这会使得器件的暗电流比可见光探测器更大[16−19].而且通常工作波长超过3µm的探测器都需要在低温下工作来获得较好的信噪比,但制冷系统增加了整个器件的尺寸和重量,使成本上升[20−23].半导体低维材料用来作为长波长和低暗电流的探测器是一种很好的选择,之前也有大量研究对此进行了尝试.例如,基于量子阱子带跃迁的量子阱红外探测器(quantum well infrared detector,QWIP)得到了广泛的研究并取得了较大的进展.该器件利用了一维有限深势阱中产生的分立的子能级间跃迁,从束缚态到准连续态这种工作模式.其中,n类QWIP对垂直正入射光无法吸收,p类QWIP虽然可以吸收,但是由于空穴的载流子迁移率较低,传输特性和灵敏度受到限制,子带光电探测器实质上是非本征探测器,器件的量子效率较低[24,25].而利用低维材料的带间跃迁则可能实现较好的性能.如果器件的大部分都是宽带隙材料,可以降低暗电流、减小噪声,利用量子阱中少部分的窄带隙材料则可以实现对长波红外的吸收.与传统体材料探测器相比,在这种结构中,由于窄带隙材料的厚度减小,热生成载流子的数目大幅减少,因此可以实现暗电流的降低.

但是半导体低维材料带间跃迁的缺点也是显而易见的,正如前文提到的,传统半导体物理理论认为,由于光生载流子只能通过热电子发射和隧穿从局域态进入连续态[26−28],所以半导体低维材料中的光生载流子由于势垒的存在,大部分被限制在局域态中,不能有效地进入外电路形成光电流,所以器件的外量子效率很低.其次,对于大部分直接带隙半导体材料来说,带边的吸收系数在103cm−1量级,这就需要吸收层材料的厚度达到数微米级才能完全吸收[29].然而如果进行失配外延,只能实现有限厚度的生长,否则就会形成失配缺陷,这会大大影响器件的性能[30−33].

近期的实验发现,处于p-n结耗尽区中的低维结构可以实现高效率的光-电转换.本文采用共振激发光致发光光谱技术,表征了受限光生载流子的逃逸过程,测量结果包含了热、输运、弛豫等多个过程的贡献.局域载流子反常的高效抽取现象和吸收系数的增大解决了前文提到的工作波长和暗电流之间的矛盾,为低维半导体材料应用于光伏领域提供了理论基础,并为高温工作红外探测器的研制提供了一条新的技术路线.

2 实 验

2.1 测试方案设计

低维半导体结构的光致发光主要有两种激发模式——非共振激发和共振激发[34,35].在非共振激发情况下,光生载流子不仅在势阱中产生,而且还在势垒中产生,所以光致发光荧光强度的变化不仅与势阱中的非辐射复合强度相关,还与载流子在势垒中的输运有关.而在共振激发条件下,光生载流子只在势阱中产生,而势垒中没有光生载流子产生.因此,在共振激发条件下,若忽略非辐射复合的影响,在开/短路条件下光致发光荧光强度的变化直接反映出在短路时光生载流子由局域态能级进入连续态的能力,如图1所示.

图1 实验原理图Fig.1.Schematic diagram of experimental principle.

为了进一步探索半导体低维结构中产生的共振激发光生载流子光致发光光谱在短路条件下的淬灭现象,测量了不同入射光功率时开路和短路条件下光致发光光谱积分强度的变化情况.此后,测量了器件开路电压和短路电流随激发光功率的变化,得到此种结构器件的工作模式.

2.2 实验过程

InAs/GaAs多量子点样品在VG V80H的分子束外延系统上生长而成.具有p-n结和n-n结的量子点样品生长在半绝缘GaAs衬底上,样品A在半绝缘GaAs衬底上生长10个周期的InAs量子点,由50 nm GaAs隔开,两侧是n-n结.样品B本征区结构与样品A一样,只是两侧电极为p-n结.两个样品的微观结构示意图见图2(a)和图2(b).

InGaAs/GaAs多量子阱样品C生长在半绝缘GaAs衬底上,GaAs p-n结中插入了20个周期的InGaAs量子阱结构,其结构示意图如图2(c).

在实验室自主搭建的荧光光谱设备上进行低温荧光测试.荧光测试系统包括:半导体红外激光器、声光可调滤光器型近红外光谱仪、金属膜衰减片、平凸透镜组件、斩波器、氦气循环制冷可控温杜瓦样品平台、光谱仪、光电探测器、SR830锁相放大器、测试软件等设备.样品引出电极用缩醛胶粘到控温冷头上,机械泵抽真空,温控仪和液氦压缩机调节样品温度,渐变金属膜衰减片调节激发激光功率密度.

光电流测试亦是采用实验室自主搭建的测试系统,包括:半导体红外激光器、金属膜衰减片、平凸透镜组件、Keithley4200-SCS半导体参数分析仪等.

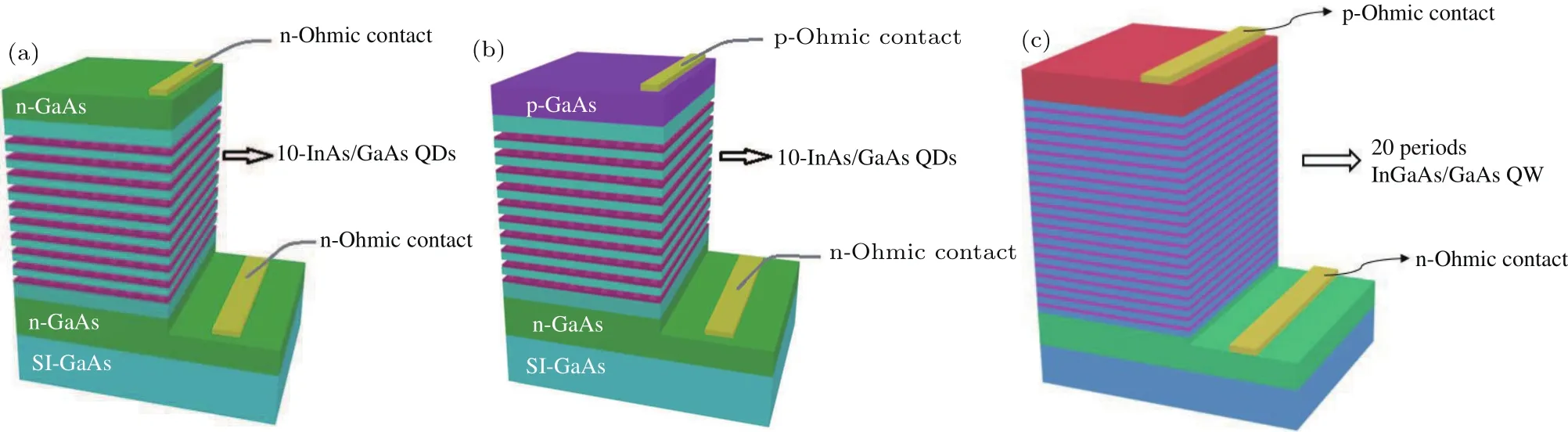
图2 器件结构示意图[36] (a)具有n-n结的InAs/GaAs多层量子点结构;(b)具有p-n结的InAs/GaAs多层量子点结构;(c)InGaAs/GaAs多量子阱原型器件结构Fig.2.Schematic of samples[36]:(a)InAs/GaAs multilayer quantum dots(QDs)structure within n-type and n-type GaAs;(b)InAs/GaAs multilayer quantum dots structure within n-type and p-type GaAs;(c)InGaAs/GaAs multilayer quantum well(QW)prototype photon detector.

3 结果与分析

3.1 具有n-n结多层InAs/GaAs量子点结构的载流子输运特性

样品A含有10个周期InAs/GaAs量子点的n-n结结构.在150 K条件下,分别在开路和外加0.7 V偏压条件下,用波长为915 nm的激光照射,测试其共振激发光致发光光谱.图3(a)是样品A在150 K条件下,915 nm激发波长、激发光功率为65 mW时开路和外加0.7 V偏压条件下的光致发光光谱.通过高斯拟合,InAs量子点光致发光光谱的半高全宽约为72.6 meV,符合量子点大小分布非均匀展宽特性.相比于样品A在开路条件下的结果,在外加0.7 V偏压条件下,共振激发的光致发光光谱的积分强度降低了7.3%,由于量子限制斯塔克效应,峰位红移了2 nm,峰位的红移也证明了外加偏压已经加到了量子点上.图3(b)是样品A在开路和外加0.7 V偏压条件下改变入射激光功率,其光致发光光谱积分强度和峰位的变化情况.样品A在开路和外加0.7 V偏压条件下光致发光光谱的积分强度随激发功率呈线性变化.当激发功率从60 mW降低到5 mW,在0.7 V偏压下的光致发光光谱强度与开路条件下强度的比例从90%降低到65%.随着激光功率的增加,样品A在开路和外加0.7 V偏压条件下光致发光光谱峰位蓝移.这是由于随着激光功率增加,量子点中的能带填充效应引起的.图3(c)是样品A在变功率开路条件下的光致发光光谱;图3(d)是样品A在外加0.7 V偏压条件下,光致发光光谱随激发激光功率的变化.

样品A在开路和外加0.7 V偏压的条件下,光致发光光谱强度变化较小,符合经典半导体物理理论,量子点中共振激发的光生载流子由于量子限制效应不能逃逸出量子点势阱而倾向于进行辐射复合发光.

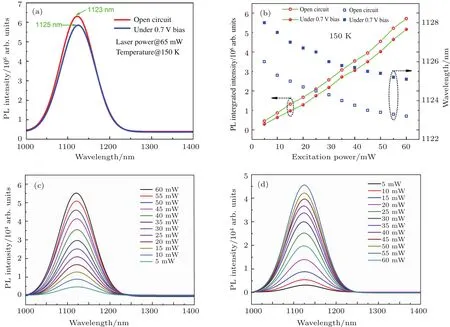
图3 样品A在150 K,波长915 nm激光共振激发下的光致发光光谱[36,37] (a)样品A在开路和外加0.7 V偏压条件下的光致发光光谱;(b)样品A在开路和外加0.7 V偏压条件下不同激发光功率时的光致发光光谱积分强度和峰位变化情况;(c)样品A在开路条件下光致发光光谱随激发光功率的变化情况;(d)样品A在外加0.7 V偏压下光致发光光谱随激发光功率的变化情况Fig.3.The photoluminescence(PL)spectra of sample A under resonant excitation at the wavelength of 915 nm at 150 K[36,37]:(a)The PL spectra of sample A measured for the open-circuit condition and with a 0.7 V bias respectively;(b)excitation-power-dependent PL integrated intensity and peak wavelength of the PL spectrum for the open-circuit and 0.7 V bias conditions;(c)excitation-power-dependent PL of sample A for the open-circuit condition;(d)excitation-power-dependent PL of sample A under 0.7 V bias conditions.

3.2 具有p-n结多层InAs/GaAs量子点结构的载流子输运特性

样品B是含有10个周期InAs/GaAs量子点的p-n结结构.本征耗尽区结构与样品A相同,区别是样品B具有p-n结结构,样品示意图见图2(b).

测试了样品B在开路和短路条件下的共振激发光致发光光谱.图4(a)是样品B在150 K、激发功率为65 mW、短路和开路下的共振激发光致发光光谱.从图4(a)可以看出,在共振激发条件下,样品B在开路条件下光致发光光谱强度高,峰形好,与样品A在开路条件下相似.但是当在杜瓦外面将样品B的p电极和n电极引出的线路短接时,样品B的共振激发光致发光光谱积分强度出现了大幅下降,降低到开路条件下的12%,这意味着InAs量子点中大约有88%的共振激发光生载流子没有参与辐射复合发光.在波长为915 nm、功率为65 mW的激光照射下,样品B的光生开路电压约为0.57 V,而样品A的外加偏压为0.7 V,略高于样品B的开路电压,但是在无p-n结的样品A中没有发生类似于样品B中的光致发光光谱强度下降这一现象.

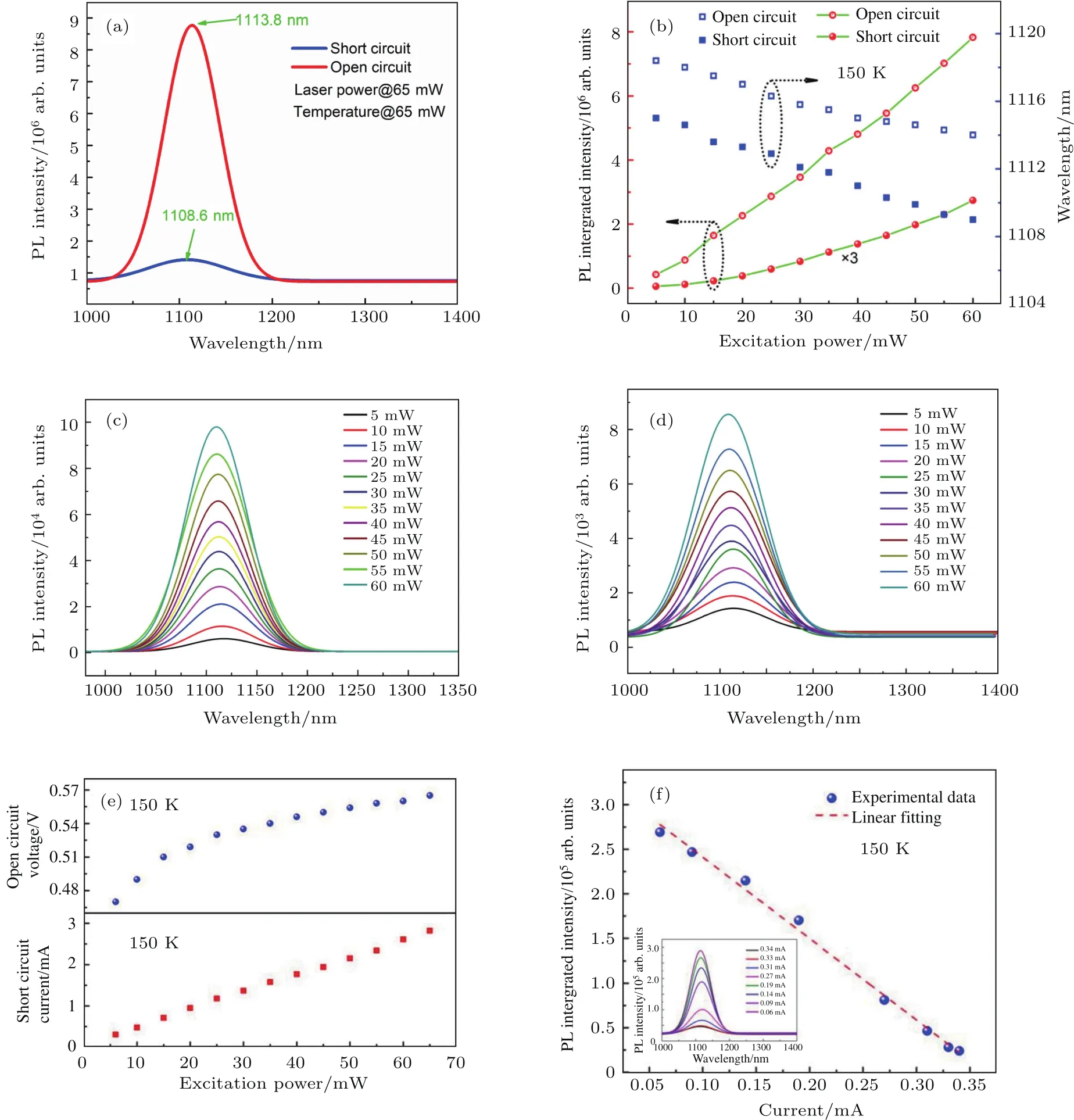
图4 样品B在150 K,波长915 nm激光共振激发下的光致发光光谱[36] (a)样品B在开路和短路条件下的光致发光光谱;(b)样品B在开路和短路条件下不同激发光功率下的光致发光光谱积分强度和峰位变化情况;(c)样品B在开路条件下光致发光光谱随激发光功率的变化情况;(d)样品B在短路条件下光致发光光谱随激发光功率的变化情况;(e)样品B的短路电流和开路电压随激发光功率的变化情况;(f)样品B外电路中加入不同阻值电阻,光致发光光谱积分强度与电流的关系Fig.4.The PL spectra of sample B under resonant excitation at the wavelength of 915 nm at 150 K[36]:(a)The PL spectra of sample B measured for the open-and short-circuit conditions respectively;(b)excitation-powerdependent PL integrated intensity and peak wavelength of the PL spectrum for the open-and short-circuit conditions;(c)excitation-power-dependent PL of sample B for the open-circuit condition;(d)excitation-power-dependent PL of sample B for the short-circuit condition;(e)excitation-power-dependent open-circuit voltage(Voc)and shortcircuit current(Jsc)at 150 K;the Jscis proportional to the incident light intensity,and the Vocis proportional to the logarithm of the incident light intensity;(f)inversely linearly related circuit current and PL intensity of sample B under a 65-mW excitation power at 150 K.

为了进一步探索样品B InAs量子点共振激发产生的光生载流子在短路条件下的淬灭现象,我们使入射激光功率从5 mW到60 mW之间均匀变化,测试其开路和短路条件下光致发光光谱积分强度和峰位的变化情况,如图4(b)所示.从图4(b)可以看出,样品B在开路条件下,随着激发功率从5 mW增加到60 mW,光致发光光谱积分强度基本呈线性增加.但是,在短路条件下,光致发光光谱强度呈抛物线增加.随着激发功率的增加,样品B在短路条件下的光谱积分强度与开路条件下的积分强度的比值从5%增加到11.6%.这表明样品B在短路条件下的光致发光光谱淬灭现象于不同功率激发条件下普遍存在.图4(c)是样品B在开路条件下光致发光光谱随激发光功率变化情况.图4(d)是样品B在短路条件下光致发光光谱随激发光功率变化情况.

为了探索样品短路条件下没有参与辐射复合发光的那部分共振激发光生载流子的去向,在915 nm激光照射下测试了样品B随入射激光功率增加时的开路电压和短路电流变化情况,如图4(e)所示.从图4(e)可以看出,样品B的短路电流Jsc随着入射激光功率的增加呈线性增加,而开路电压Voc与入射激光功率的增加呈对数关系.对于带隙为Eg的p-n结太阳能电池,光电流为

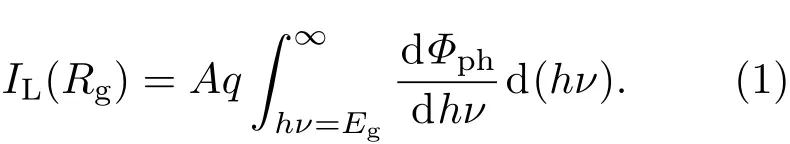
从(1)式可以看出,光电流与入射光通量成正比.在本实验中,光电流,即样品B的短路电流与入射激光强度呈线性关系.p-n结太阳能电池光照下的典型I-V特性,开路电压为

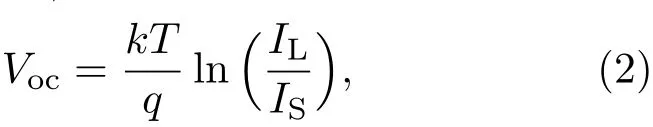
其中,IS是饱和电流,与p-n结掺杂和材料带隙有关.可以认为样品B中的饱和电流是固定值,开路电压与光电流呈对数关系.由于上面算出光电流与入射光功率成正比,可依此推算出p-n结太阳能电池的开路电压与入射光功率呈对数关系.从图4(e)可以看出,样品B在915 nm激光共振激发下,短路电流和开路电压随光功率的变化遵循经典p-n结太阳能电池的I-V特性.但是按照经典半导体理论,量子点具有三维量子限制效应,共振激发的载流子不能逃逸出载流子而倾向于进行辐射复合发光.该实验现象与之前的理论相悖.

为了得到光生载流子的逃逸路线,我们将一个滑动变阻器串联到样品B的电路中,调节滑动变阻器电阻,改变整个电路的电流,测试其共振激发荧光强度变化,如图4(f)所示.从图4(f)可以看出,短路电流和光致发光荧光强度呈线性负相关.根据以上结果可以推断出从InAs量子点中逃逸的共振激发光生载流子主要用于产生光电流,这预示着具有p-n结的量子点结构可以应用于太阳能电池和光电探测器.

从以上实验可以看出,在短路条件下,样品B量子点中共振激发的光生载流子直接逃逸出量子点产生光伏效应.然而,在n-n结的样品A通过加0.7 V外偏压模拟样品B的内建电场,但是量子点中共振激发的光生载流子倾向于弛豫到基态进行辐射复合.因为样品A和样品B具有相同的势垒高度和厚度,所以热电子发射和隧穿理论不能用来解释共振激发载流子从量子点中逃逸出电路形成电流这种现象[28,38−40].

3.3 逃逸机理分析

我们通过计算和比较载流子漂移出量子点的时间和弛豫回基态的时间来估算量子点中共振激发载流子直接逃逸出量子点而不弛豫到基态辐射复合发光的概率.根据文献[41]中的描述,量子点中激发态电子弛豫到基态大约有几百皮秒.而样品B在短路条件下,分辨出量子点中激发态自由载流子渡越出量子点还是弛豫到基态能级对于解释实验现象非常重要.自由激发态载流子渡越出耗尽区的量子点的时间为

其中,h表示量子点的高度,v表示电子或者空穴的漂移速度.电子在InAs和GaAs中的迁移率都大于2000 cm2·V−1·s−1, 空穴迁移率大于100 cm2·V−1·s−1[42]. 经过计算, 电子或者空穴逃逸出量子点的时间在飞秒量级.因此共振激发的激发态自由载流子逃逸出量子点而不是弛豫回基态进行复合发光,是存在时间上的可能性.

对于样品A,当外加一个偏压在量子点结构上时,本征区中电场分布是均匀的,载流子漂移速率与电场和载流子迁移率成比例.电子的迁移率比空穴的迁移率高,导致电子的漂移速率大于空穴的漂移速率,从而导致了过量的空穴聚集在器件本征区形成一个大的正电场,阻止了后续载流子逃逸,即产生了库仑阻塞效应.然而,对于样品B,在耗尽区,电场随着结的距离线性增加,达到最大值后线性减小,最后减小为零.电场的斜率可以通过调节p区或者n区的掺杂浓度来调节,如图5所示.p-n结可以调节电场分布来使空穴充分被抽取走,达到一个较好的电中性条件.p-n结的这种独特性质缓解了库仑阻塞效应,使量子点中的载流子持续逃逸到外电路中.

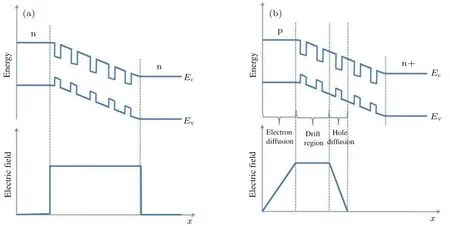
图5 样品A和样品B中本征区的电场分布[37]Fig.5.Distribution of the electric field of intrinsic region of sample A and sample B[37].

尽管p-n结中受限光生载流子逃逸的清晰物理图像尚未建立,但仍有必要对其光电转换能力进行评估.在样品B中,当入射激光功率为65 mW时,实测短路电流为2.82 mA,因此光电转换效率为5.9%,计算得到10层InAs量子点吸收系数约为104cm−1.我们在计算吸收系数时没有减去反射的入射光,并且认为p-n结的载流子抽取效率为100%,因此实际的吸收系数应大于该数值.尽管如此,104cm−1的数值仍远大于理论计算得到的量子点材料的光吸收系数(约100 cm−1)[43,44],并接近于GaAs体材料在其带隙处的吸收系数[45].考虑到零维半导体材料低的态密度和局域态波函数,我们认为p-n结的加入增加了InAs量子点的吸收系数,证明量子点可以应用于太阳能电池和光电探测器.

根据以上结果,我们提出了一个可能的模型来解释上述现象.具有p-n结结构的量子点中在短路条件下的光生载流子的终态是自由激发态,在内建电场的作用下直接逃逸出量子点进入势垒导带,进而流入外电路形成短路电流,如图6(b)所示.在样品A中,具有n-n结的外加偏压下,量子点中的光生载流子弛豫到基态进行辐射复合发光,而没有流出外电路,如图6(a)所示.

根据量子力学的微扰理论,吸收系数与态密度和载流子终态的波函数有关[46],在量子点中,载流子的终态应该是局域态的基态.但是,在本实验中,具有p-n结的量子点在短路条件下的终态却是自由态.这种物理属性的改变增加了具有p-n结的量子点在短路条件下的吸收系数,在这种情况下,不能认为吸收系数是一个常数,这对应用于太阳能电池和探测器具有很重要的启示.

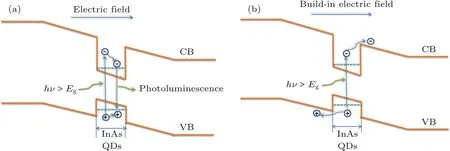
图6 InAs量子点中光子吸收和载流子输运模型[36] (a)样品A外加0.7 V偏压时,InAs量子点的光子吸收和载流子输运过程;(b)样品B在短路条件下,InAs量子点的光子吸收和载流子输运过程Fig.6.Sketch of the photon absorption and carrier transportation processes of InAs quantum dots embedded in GaAs with a p-n junction[36]:(a)Schematic diagram of the established photon absorption and carrier transportation processes;(b)schematic diagram of the new photon absorption and carrier transportation processes.

3.4 具有p-n结多层InAs/GaAs量子点结构的吸收系数增强特性

在具有p-n结的InAs/GaAs量子点结构短路条件下,光致发光光谱发生淬灭,同时测量短路电流,推断在短路条件下量子点中共振激发光生载流子不弛豫到基态进行辐射复合,而是逃逸出外电路,估算该结构在短路条件下吸收系数增加,可达104cm−1.InAs量子点吸收系数的增加表明在太阳能电池和光电二极管探测器方面具有广阔的应用前景.探测器主要是在反偏条件下探测光电转换.为了测量样品B在外加偏压下吸收系数和外加偏压的关系,我们测量了样品的透射光.激光器入射光线与样品垂直平分面呈30◦,同时用两个功率计测试反射光和透射光,改变外加偏压,同时测量透射光功率和外电流的变化,测试结果如图7所示.半导体中的吸收系数和透射光功率的关系为[46]

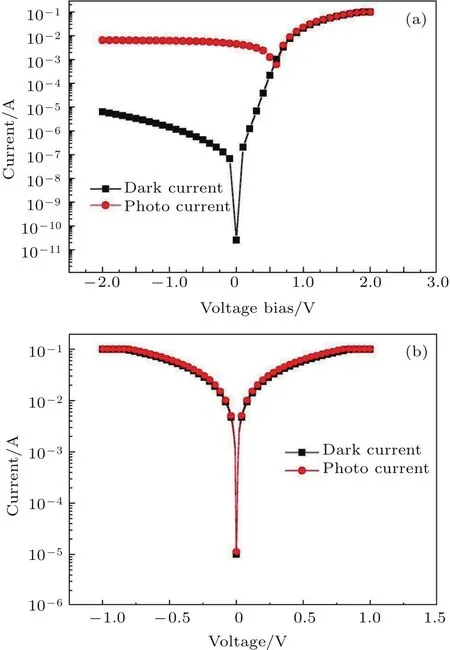
图7 (a)样品B的光电流和暗电流谱;(b)样品A的光电流和暗电流谱[37]Fig.7.(a)Current-bias curves of InGaAs/GaAs quantum well photo diode measured under 915 nm illumination and dark condition of sample B;(b)currentbias curves of InGaAs/GaAs quantum well photo diode measured under 915 nm illumination and dark condition of sample A[37].

其中,λ是入射激光的波长,Sn是能量为E附近|0,n⟩每单位能量的态密度,c是光速.如果样品B在短路条件下,InAs量子点的能级处于连续态而不是局域态,态密度Sn会变大,进而增加吸收系数.

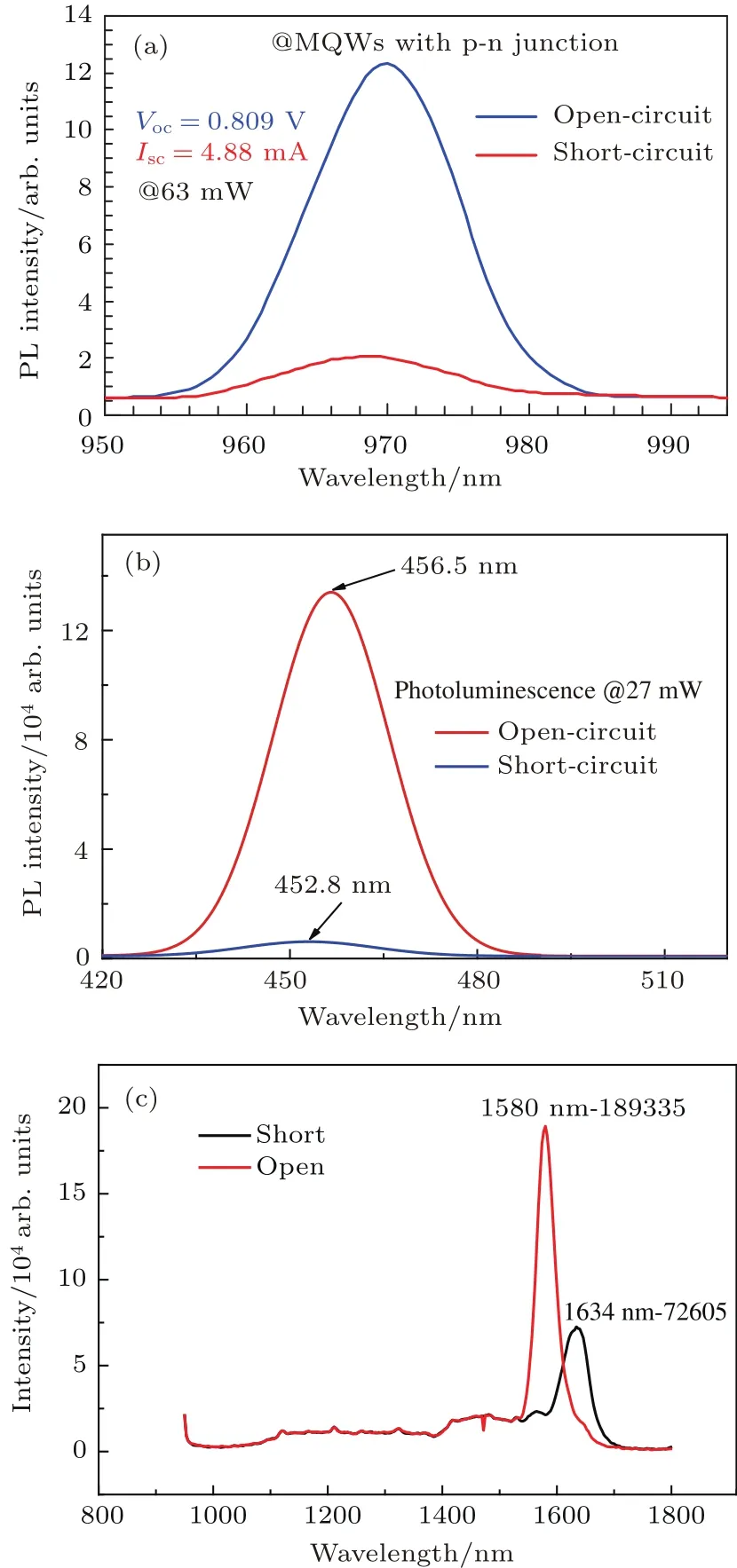
图8 (a)In0.2Ga0.8As/GaAs多量子阱样品在开路和短路下的光致发光光谱;(b)In0.15Ga0.85N/GaN多量子阱样品在开路和短路下的光致发光光谱;(c)In0.53Ga0.47As/In0.52Al0.48As/InP复合多量子阱样品在开路和短路下的光致发光光谱[47,48]Fig.8.(a)The PL spectra of In0.2Ga0.8As/GaAs multiple quantum well structure under open-and short-circuitconditionsrespectively; (b)thePL spectra of In0.15Ga0.85N/GaN multiple quantum well structure under open-and short-circuit conditions respectively; (c) the PL spectra of In0.53Ga0.47As/In0.52Al0.48As/InP compositemultiple quantum wellstructure underopen-and short-circuit conditions respectively[47,48].

光电二极管型探测器主要是在外加反向偏压下工作,图7(a)和图7(b)分别是样品A和样品B在915 nm激光照射下的光电流I-V图和暗电流I-V图.对比图7(a)和图7(b)可以看出,样品B在反偏条件下吸收系数和净光电流大,暗电流小,信噪比高.因此具有p-n结的InAs量子点在近红外探测领域具有很好的应用前景.

3.5 实用性验证:普适性和重复性

除了在InAs量子点结构中发现光生载流子高效抽取现象,我们还在In0.2Ga0.8As/GaAs量子阱和In0.15Ga0.85N/GaN量子阱以及In0.53Ga0.47As/In0.52Al0.48As/InP量子阱中得到了相同的实验结果,如图8(a)—(c)所示.

在含有p-n结的In0.2Ga0.8As/GaAs量子阱结构中,我们观察到87.3%的光生载流子通过p-n结从量子阱中逃逸出来形成光电流而非弛豫到量子阱的基态能级;在In0.15Ga0.85N/GaN量子阱中,超过95%的光生载流子形成光电流而不是辐射复合发光;在In0.53Ga0.47As/In0.52Al0.48As/InP量子阱结构中,则是有62%的光生载流子逃逸出量子阱.以上的结果表明,p-n结中低维半导体结构中光生载流子高效抽取现象在各种材料体系中是普遍存在的,具有普适性和重复性.

3.6 实用性验证:InGaAs/GaAs带间跃迁量子阱红外探测器原型器件

利用p-n结中低维半导体结构载流子高效抽取现象,制备了带间跃迁量子阱红外探测器(interband transition quantum well infrared detector,IQWIP)原型,其器件结构如图2(c)和图9所示.20个周期的In0.2Ga0.8As/GaAs多量子阱插于GaAs p-n结中,光致发光荧光谱和响应光谱如图10所示,光致发光峰位于956 nm处,位于肩部869 nm处的峰是GaAs体材料的峰.从响应光谱中可以看出,位于GaAs体材料吸收峰长波方向的是InGaAs量子阱的吸收峰,吸收峰相对荧光峰有明显的蓝移.不同光照强度下的电流电压曲线和不同光功率密度下的量子效率如图11(a)和图11(b)所示.在无表面减反射膜的实验条件下,利用仅100 nm的有效吸收厚度实现了31%的外量子效率;实测表面反射率为40%—50%,故实际量子效率水平接近60%.基于该数值推算得到量子阱的光吸收系数达到3.7×104cm−1,该数值高于传统透射实验测量结果一个数量级.

图9 光学显微镜下器件形貌图Fig.9.Morphology of the device under optical microscope.

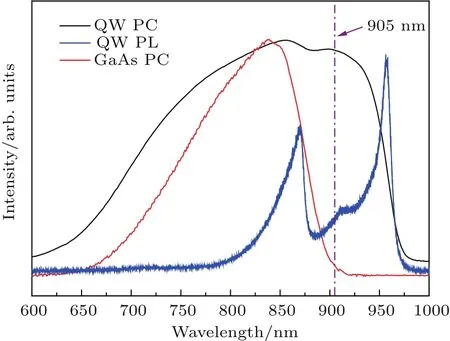
图10 InGaAs/GaAs多量子阱原型器件光致发光荧光谱和响应光谱[49]Fig.10.The PL spectra and response spectra of In-GaAs/GaAs multiple quantum well prototype[49].

根据原有的理论,低维半导体结构载流子的抽取效率低,吸收系数较小,在光电转换应用的性能较差.而我们的实验表明,通过在低维半导体结构外加优化的p-n结,可以实现大于90%的抽取效率,吸收系数大于相应的体材料,可以很好地用于光电转换.

3.7 实用性验证:InAsSb/GaSb IQWIP原型器件

扩展波长短波红外和中波红外探测器由于暗电流较大,通常需要工作在低温下,利用p-n结中载流子的高效抽取效应,实现了基于InAsSb/GaSb材料的带间跃迁扩展波长短波红外量子阱探测器,在室温下性能优异.

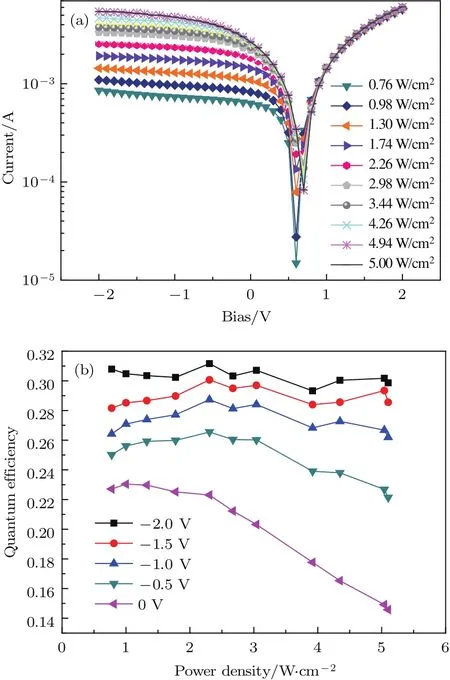
图11 (a)不同光照强度下的电流电压曲线;(b)不同光功率密度下的量子效率[49]Fig.11. Illumination powerdependenton the(a)current-bias curve and(b)quantum efficiency of the In0.2Ga0.8As/GaAs quantum well photodiode[49].

10个周期的InAs0.91Sb0.09/GaSb多量子阱置于GaSb p-n结中,器件结构如图12(a)所示.通过计算得到5 nm厚的InAs0.91Sb0.09量子阱的带隙约为0.53 eV(2.35µm),可以覆盖从短波红外到长波红外的整个波段.此器件有较窄的波长响应范围,从2µm到2.3µm,在2.1µm处达到峰值,如图12(b),左侧1.87µm处是GaSb势垒的吸收峰;而右侧位于2.1µm处的峰对应于InAsSb量子阱带间跃迁.

器件的变温暗电流谱如图12(c)所示.当温度从300 K降低到200 K时,暗电流随温度迅速减小,这是由于扩散电流被抑制引起的.温度继续降低,暗电流减小缓慢,这是因为温度低于200 K后,产生复合电流成为主要的暗电流源.

在无减反膜的条件下,其峰值响应度在−500 mV时为0.4 A/W,对应量子效率为23.8%.300 K时,−400 mV和零偏的暗电流分别为6.05×10−3A/cm2和3.25×10−5A/cm2,峰值探测率出现在零偏条件下,为6.91×1010cm·Hz1/2·W−1. 这个结果已经优于目前大部分的III/V族红外探测器,并与HgCdTe探测器性能相当,如果继续优化材料,可以期待有更好的性能.

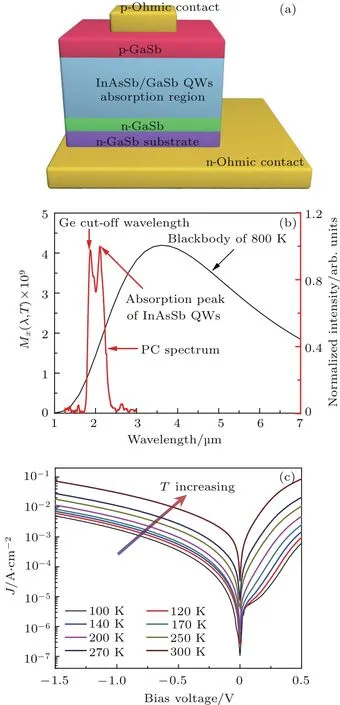
图12 (a)InAs0.91Sb0.09/GaSb多量子阱红外探测器结构图;(b)InAs0.91Sb0.09/GaSb多量子阱红外探测器样品的响应光谱;(c)InAs0.91Sb0.09/GaSb红外探测器样品的变温暗电流曲线[50]Fig.12.(a)Schematic diagram of the InAs0.91Sb0.09/GaSb QWs photodetector;(b)typical normalized relative photocurrent spectral response curves of InAs0.91Sb0.09/GaSb QWs;(c)dark current densities versus applied bias voltage of the photodetector for di ff erent temperatures[50].

4 结 论

实验上在多种材料体系中均观察到p-n结中受限光生载流子的反常高效抽取效率和反常吸收系数增加两个现象,利用该现象研制了近红外900 nm波段工作原型器件,计算得到的吸收系数达到3.7×104cm−1,比先前报道的高一个数量级.利用p-n结对载流子高效抽取效应,设计了新型IQWIP器件并进行了近红外波段的原型器件验证.在IQWIP器件中,实现了保持较低暗电流水平的同时将响应波长增大,且在拓展的波段范围仍具有较好的量子效率.尽管目前的实验结果仅为近红外波段,但利用GaSb基窄禁带半导体材料或HgCdTe材料,有望将器件的工作波长拓展至中波红外范围.此外,由于IQWIP的新颖工作原理和特殊的结构特征,该器件还有望实现新型高性能光电晶体管、低成本高性能太阳能电池等器件.

[1]Goetzberger A,Hebling C,Schock H W 2003 Mater.Sci.Engineer.R:Rep.40 1

[2]Jenny D,Loferski J,Rappaport P 1956 Phys.Rev.101 1208

[3]Chapin D M,Fuller C,Pearson G 1954 J.Appl.Phys.25 676

[4]Gloeckler M,Sankin I,Zhao Z 2013 IEEE J.Photovolt.3 1389

[5]Chirilǎ A,Buecheler S,Pianezzi F,Bloesch P,Gretener C,Uhl A R,Fella C,Kranz L,Perrenoud J,Seyrling S 2011 Nat.Mater.10 857

[6]Rogalski A 2005 Rep.Prog.Phys.68 2267

[7]Callewaert F,Hoang A,Razeghi M 2014 Appl.Phys.Lett.104 053508

[8]Liu S T,Quan Z J,Wang L 2017 Chin.Phys.B 26 038104

[9]Nelson J 2003 The Physics of Solar Cells(London:World Scienti fi c Publishing Company)pp19–37

[10]Rogalski A 2010 Infrared Detectors(Florida: CRC Press)pp295–338

[11]Basu P K 1997 Theory of Optical Processes in Semiconductors:Bulk and Microstructures(Vol.4)(Oxford:Clarendon Press)pp80–122

[12]Dahal R,Pantha B,Li J,Lin J,Jiang H 2009 Appl.Phys.Lett.94 063505

[13]Grundmann M 2015 The Physics of Semiconductors:An Introduction Including Nanophysics and Applications(Heidelberg:Springer)

[14]Qiu W,Hu W,Lin C,Chen X,Lu W 2016 Opt.Lett.41 828

[15]Bai Z Z,Xu Z C,Zhou Y,Yao H C,Chen H L,Chen J X,Ding R J,He L 2015 J.Infrared Millim.Wave 34 716(in Chinese)[白治中,徐志成,周易,姚华城,陈洪雷,陈建新,丁瑞军,何力2015红外与毫米波学报34 716]

[16]Rogalski A,Antoszewski J,Faraone L 2009 J.Appl.Phys.105 091101

[17]Hu W D,Liang J,Yue F Y,Chen X S,Lu W 2016 J.Infrared Millim.Wave 35 25(in Chinese)[胡伟达,梁健,越方禹,陈效双,陆卫2016红外与毫米波学报35 25]

[18]Liu D,Lin C,Zhou S,Hu X 2016 J.Electron.Mater.45 2802

[19]Ye Z,Zhang P,Li Y,Chen Y,Zhou S,Huang Y,Sun C,Lin C,Hu X,Ding R 2014 Opt.Quantum Electron.46 1283

[20]Rogalski A 2003 Prog.Quantum Electron.27 59

[21]Maimon S,Wicks G 2006 Appl.Phys.Lett.89 151109

[22]Chakrabarti S,Sti ff-Roberts A,Bhattacharya P,Gunapala S,Bandara S,Rafol S,Kennerly S 2004 IEEE Photon.Technol.Lett.16 1361

[23]Freundlich A,Lombez L,Sugiyama M 2016 Proc.SPIE 9743 974301

[24]Rogalski A 2003 J.Appl.Phys.93 4355

[25]Levine B 1993 J.Appl.Phys.74 R1

[26]Ridley B 1991 Rep.Prog.Phys.54 169

[27]Luque A,Martí A 2011 Nat.Photon.5 137

[28]Xu Z Y,Lu Z D,Yang X,Yuan Z,Zheng B,Xu J,Ge W,Wang Y,Wang J,Chang L L 1996 Phys.Rev.B 54 11528

[29]Casey Jr H,Sell D,Wecht K 1975 J.Appl.Phys.46 250

[30]Green M A 2008 Solar Energy Materials and Solar Cells 92 1305

[31]Mooney P,LeGoues F,Terso ffJ,Chu J 1994 J.Appl.Phys.75 3968

[32]Jain S,Willander M,Maes H 1996 Semicond.Sci.Technol.11 641

[33]Dunstan D,Young S,Dixon R 1991 J.Appl.Phys.70 3038

[34]Chatterjee S,Ell C,Mosor S,Khitrova G,Gibbs H M 2004 Phys.Rev.Lett.92 067402

[35]Kaindl R A,Carnahan M A,Hagele D,Lovenich R,Chemla D S 2003 Nature 423 734

[36]Wang W,Wang L,Jiang Y,Ma Z,Sun L,Liu J,Sun Q,Zhao B,Wang W,Liu W,Jia H,Chen H 2016 Chin.Phys.B 25 097307

[37]Wang W Q 2017 Ph.D.Dissertation(Beijing:University of Chinese Academy of Sciences)(in Chinese)[王文奇2017博士学位论文(北京:中国科学院大学)]

[38]Li T,Bartolo R E,Dagenais M 2013 Appl.Phys.Lett.103 141113

[39]Antolín E,Marti A,Farmer C,Linares P,Hernández E,Sánchez A,Ben T,Molina S,Stanley C,Luque A 2010 J.Appl.Phys.108 064513

[40]Kapteyn C,Heinrichsdor ffF,Stier O,Heitz R,Grundmann M,Zakharov N,Bimberg D,Werner P 1999 Phys.Rev.B 60 14265

[41]Heitz R,Veit M,Ledentsov N N,Ho ff mann A,Bimberg D,Ustinov V M,Kop’ev P S,Alferov Z I 1997 Phys.Rev.B 56 10435

[42]Harrison J,Hauser J 1976 J.Appl.Phys.47 292

[43]Luque A,Mellor A,Ramiro I,Antolín E,Tobías I,Martí A 2013 Solar Energy Materials and Solar Cells 115 138[44]Mellor A,Luque A,Tobías I,Martí A 2014 Adv.Funct.Mater.24 339

[45]Sturge M 1962 Phys.Rev.127 768

[46]Elliott R 1957 Phys.Rev.108 1384

[47]Sun Q L,Wang L,Jiang Y,Ma Z G,Wang W Q,Sun L,Wang W X,Jia H Q,Zhou J M,Chen H 2016 Chin.Phys.Lett.33 106801

[48]Wu H Y,Ma Z G,Jiang Y,Wang L,Yang H J,Li Y F,Zuo P,Jia H Q,Wang W X,Zhou J M,Liu W M,Chen H 2016 Chin.Phys.B 25 117803

[49]Liu J,Wang L,Jiang Y,Ma Z G,Wang W Q,Sun L,Jia H Q,Wang W X,Chen H 2017 J.Infrared Millim.Wave 36 129(in Chinese)[刘洁,王禄,江洋,马紫光,王文奇,孙令,贾海强,王文新,陈弘2017红外与毫米波学报36 129]

[50]Sun L,Wang L,Lu J L,Liu J,Fang J,Xie L L,Hao Z B,Jia H Q,Wang W X,Chen H 2018 Chin.Phys.B 27 047209