金刚石氮空位中心自旋量子调控∗

刘刚钦1)2)† 邢健1) 潘新宇1)3)4)‡

1)(中国科学院物理研究所,北京凝聚态物理国家研究中心,北京 100190)

2)(香港中文大学物理系,新界沙田,香港特别行政区)

3)(量子物质科学协同创新中心,北京 100871)

4)(中国科学院拓扑量子计算卓越创新中心,北京 100190)

(2018年4月20日收到;2018年4月28日收到修改稿)

1 引 言

量子计算和量子传感近年来受到了广泛的关注,发展迅速.量子计算指充分利用量子体系的特定性质,如纠缠态和叠加态来完成计算任务[1].该领域受到关注的原因可以归为两个方面:一是随着集成电路密度越来越高,经典计算机的单比特物理尺度越来越小,逐渐进入了量子力学起支配作用的微观世界,需要发展新的计算机模型;二是量子计算在解决特定问题上拥有巨大优势,如多体系统量子模拟[2]、质因数分解[3]和搜索算法[4]等经典计算效率极低的问题.

从量子计算的原理可以看到,其核心技术就是对物理系统的量子调控,包含量子态的制备、操控和测量等过程.在量子调控过程中存在着一个矛盾:一般可以实现较快操作的体系与周围环境(包括操控带来的影响)的耦合也强,对应的量子态可用于计算的时间(相干时间)都比较短;而一般相干时间比较长的物理体系和环境耦合较弱,其量子态操控的速度就比较慢.所以寻找具有极好相干性质而且易于调控的物理系统是具有挑战性的任务.为了达到这样的效果,通常需要使用一些极端条件,比如超导量子比特需要工作在mK的温度以让环境热噪音降到极低;冷原子或者离子阱系统需要维持极高真空度以隔离周围其他粒子对系统的影响.

金刚石氮空位(nitrogen-vacancy,NV)中心是实现量子计算的优秀物理系统之一,它的最大特点是其自旋量子比特在室温下就有极长的相干时间,而且用光学方法和射频微波脉冲就可以实现极高效率的量子操控.其极长的自旋态相干时间带来了极高的磁场探测灵敏度,加上NV中心是亚纳米尺度的结构,可以稳定存在于金刚石单晶和纳米颗粒中,也便于和其他系统耦合,甚至可以进入到活细胞内部作为局域弱信号的灵敏探针.这些优势使得NV中心成为了量子计算和量子传感领域的研究热点.本文介绍NV中心单电子自旋量子调控的基本理论和主要实验技术手段,并介绍该体系近期的研究进展,包括弱耦合核自旋的探测、量子逻辑门的实现、相变增强的纳米温度计等.关于NV中心的基础知识可以参阅综述文献[5—7],量子计算相关内容见综述文献[8—10],量子传感应用见综述文献[11—13].

2 金刚石NV中心和光磁共振

2.1 物理结构和光学性质

如图1所示,NV中心是金刚石中的一种点缺陷结构,它由一个替代位的氮原子和近邻的晶格空位构成.在量子调控研究中一般考虑带负电荷的NV中心(NV−),其空位提供4个未配对成键的电子,加上氮原子贡献的1个电子和额外俘获的1个电子,这个体系可以看作总自旋为1的电子自旋[7].自旋是原子存在的內禀属性,并没有什么特殊之处,但要将单个自旋从材料体系中独立出来并用于量子调控,需要满足一些特殊条件,其中第一步就是要有实验手段可以探测到它们的存在.

NV中心拥有独特的发光性质,可以用光学方法进行探测.图1(c)所示为对一块金刚石单晶样品的共聚焦荧光扫描图像,其中一个个的亮点就是NV中心.NV中心(NV−)自旋基态和激发态之间的能量差是1.945 eV,用450—570 nm的激光都可以激发它稳定地发光,其辐射荧光波长分布在650—800 nm之间[14].由于发光来自单自旋的能级跃迁,所以NV中心是非常稳定的单光子源,用这个方法可以检验荧光扫描图中的亮点是否来自单个NV,见图1(d)中的内插图.

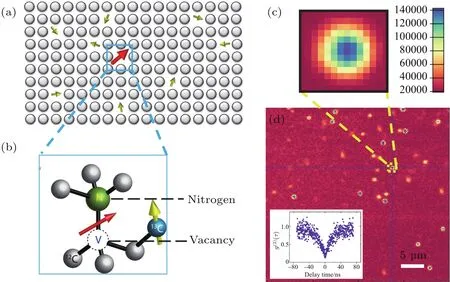
图1 NV中心结构和荧光扫描图 (a)金刚石自旋环境,其中黄色箭头表示随机分布的13C核自旋,自然丰度为1.1%;(b)NV中心由一个替代位氮原子和一个近邻空位组成;(c),(d)块材金刚石的荧光扫描图,其中(c)为(d)图的局部放大,(d)中插图为荧光子的二阶关联信号,可以检验荧光信号源是否为单光子源Fig.1.Structure of NV center and confocal images:(a)The spin bath in diamond lattice,yellow arrows represent the randomly distributed13C nuclear spins,which is about 1.1%in natural abundance;(b)NV center is formed by a substitute nitrogen atom and an adjacent vacancy;(c),(d)confocal images of a bulk diamond;the inset of panel(d)is the second-order correlation signal from a single NV center,which is a single-photon source.

2.2 自旋能级结构和光磁共振

除了提供稳定的荧光信号,NV中心的光学跃迁还提供了一种非常高效的自旋极化和读出手段[15].虽然NV中心的物理结构使得其可以看作是一个独立的电子自旋,但是在室温条件下,热涨落对应的能量(30 meV)远大于其自旋向上和向下态之间的能量差(0.01 meV∼2.87 GHz),所以室温下NV中心自旋态几乎没有极化.图2(a)绘出了NV中心自旋态依赖的光学跃迁路径,如果电子自旋一开始处于mS=0状态,它会被532 nm激光激发到激发态,并辐射荧光光子返回mS=0;如果电子自旋一开始在mS=±1的状态,532 nm激光也会将其激发,但是此时有较大概率选择右边的自旋单态路径返回,最后也回到mS=0的状态.如此重复几次,电子自旋就被极化到mS=0的状态上了.由于自旋单态部分的跃迁路径在探测窗口(650—800 nm)内没有荧光辐射,所以这个过程同时也提供一种便捷的自旋状态读出机制:电子自旋的mS=±1态比mS=0态发光强度要弱30%,只要检验NV中心的荧光强度,就可以知道一开始其自旋是处于哪个状态.

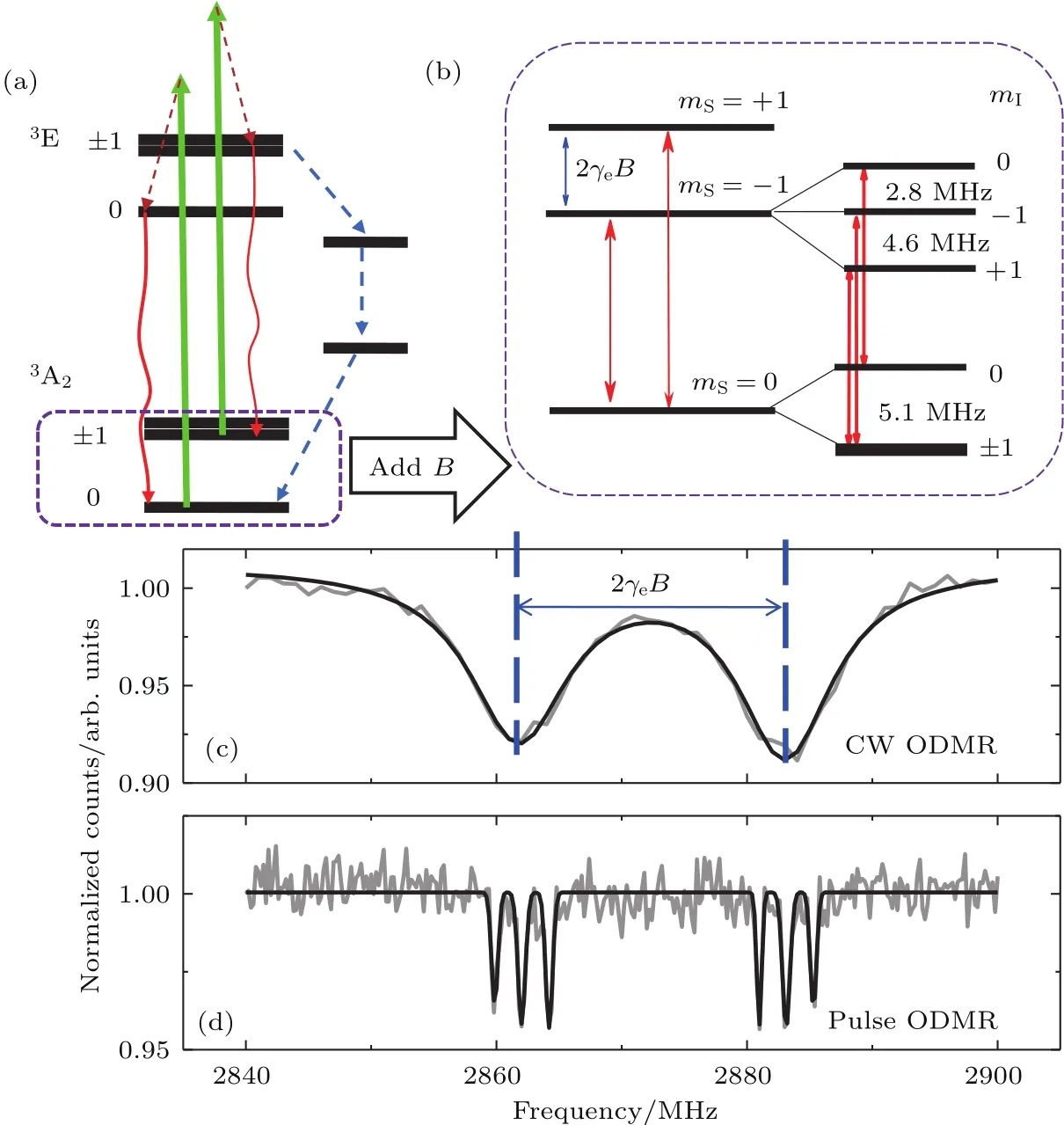
图2 光磁共振 (a)NV中心能级结构和光学跃迁;(b)外磁场下的塞曼劈裂和14N核自旋带来的精细结构;(c)典型的连续扫描光磁共振谱线,其中两个共振谷之间的距离由塞曼劈裂大小决定;(d)脉冲光磁共振谱线,可以看到14N核自旋精细结构Fig.2.Optically detected magnetic resonance(ODMR):(a)The energy structure and optical transitions of an NV center;(b)Zeeman splitting under an external magnetic fi eld and hyper fi ne structure from the host 14N nuclear spin;(c)continuous-wave ODMR spectrum,the splitting is caused by Zeeman e ff ect;(d)pulsed ODMR spectrum,the hyper fi ne structure is from the host14N nuclear spin.

下面介绍NV中心自旋态的量子操控技术.NV中心自旋基态为自旋三重态,其mS=±1和mS=0之间有2.87 GHz的零场劈裂,这个能量属于微波频段,用共振的微波脉冲就可以实现相干操控.这和电子自旋共振以及核磁共振谱仪的原理一样,都是用共振的电磁场来驱动二能级系统的受控演化.由于NV中心的自旋极化和读出用的是光学脉冲,整个过程被称为光磁共振.图2(c)是典型的光磁共振谱线,通过连续监测NV中心的荧光强度并扫描施加的微波脉冲频率而得到.当微波脉冲远离共振频率时,激光会将电子极化到mS=0的状态,此时荧光比较强而且稳定;当微波脉冲接近工作频率时,电子会有一定概率被翻转到mS=±1的状态,此时荧光会变弱,表现在谱线上的共振谷信号.

从光磁共振谱线的位置和展宽可以推算电子自旋所处的局域环境的信息[15,16].例如,由于外磁场的存在,mS=±1之间的能级简并被塞曼效应所消除,光磁共振谱线上就出现两个共振谷,从它们的位置可以得到外磁场信息.图2(c)中光磁共振谱线有较大的展宽,主要来自于连续采集方式下激光和微波的功率展宽.如果用脉冲光磁共振的方法,将激光脉冲隔离开并使用较弱的微波脉冲,可以大大提高谱线的分辨率,最终到达电子自旋相干性质所决定的展宽宽度[17].图2(d)是同一个NV在相同外磁场下的脉冲光磁共振谱线,可以清晰地看到14N核自旋的超精细结构[18].

2.3 固态浸没透镜和共面波导天线

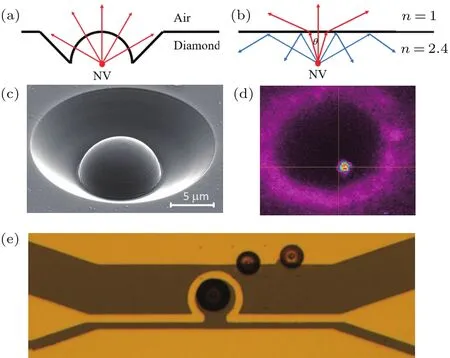
图3 固态浸没透镜和共面波导天线 (a)固态浸没透镜和(b)平面结构下荧光辐射路径;(c)固态浸没透镜的电镜图片和(d)共聚焦荧光扫描图片,直径为10µm;(e)共面波导天线的光学显微镜照片(中间包含一个固态浸没透镜)Fig.3.Solid immersion lens(SIL)and coplanar waveguide(CPW):(a),(b)The fl uorescence emission path with(a)and without(b)SILs;(c)scanning electron microscope and(d)confocal image of a SIL(diameter:10µm);(e)bright fi eld image of the CPW,with a SIL at the center.

从上面的描述中可以发现,为了实现较好的自旋量子调控,关键是提高NV中心辐射荧光的收集效率以及微波脉冲的耦合效率.如图3所示,金刚石折射率较大 (n=2.4),块材样品中NV中心辐射的部分荧光在到达表面后由于全反射效应而无法被收集到.为了解决这个问题,可以在金刚石表面加工微结构以提高荧光收集效率[19],如图3(c)所示为聚焦离子束刻蚀工艺制备的固态浸没透镜[20],其中心包含着一个NV中心,该透镜可以将NV中心的荧光收集效率大大提高,从平面结构的约100 kps提升到500 kps以上.另一方面,为了提升施加的微波脉冲的耦合效率,我们在浸没透镜的旁边用金属沉积制备了一个微波共面波导结构,使得电子自旋单次翻转可以在10 ns之内完成(见下文讨论).

3 单自旋量子调控和自旋相干性质

3.1 单自旋拉比振荡

拉比振荡是二能级系统状态在周期性外场驱动下的振荡行为.对于NV中心电子自旋而言,其拉比振荡的快慢由施加的微波场的大小和方向所决定.如图4所示,在布洛赫球面上,Z轴的投影表示自旋量子态的布居数,定义北极为|0⟩≡ |mS=0⟩态,南极为|1⟩≡ |mS=|+1⟩态,则拉比振荡对应着量子比特状态在布洛赫球面上的圆周运动.不同的旋转轴可以通过控制微波脉冲的相位来得到,而旋转角度的大小取决于微波脉冲的强度和持续时间.

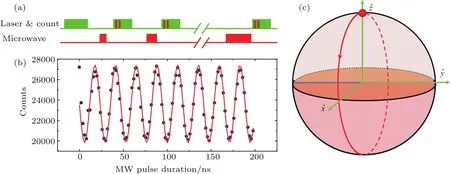
图4 拉比振荡 (a)脉冲序列;(b)典型的拉比振荡信号;(c)布洛赫球面表示Fig.4.Rabi oscillation:(a)Pulse sequence;(b)typical Rabi oscillation signal;(c)illustration in the Bloch sphere.

图4(a)是NV中心电子自旋拉比振荡的实验脉冲序列.首先是一个3µs的激光脉冲将电子自旋制备到|0⟩态,随后,一个确定长度的微波脉冲加载到样品上,它会将电子自旋制备到一个特定的状态;紧接着,用第二个激光脉冲读出并重新初始化电子自旋;电子自旋被微波操控后的状态会反映在最后的荧光信号强度上.在连续激发下,单个NV中心每秒只有5×105的光子数可以被收集到,所以在一次读出(0.3µs)中,得到的荧光光子计数是非常小的(不到1个).通常这样的脉冲序列需要重复执行105次,才能达到比较好的信噪比.图4(b)是典型的单电子自旋拉比振荡信号,由于使用了共面波导天线,微波耦合效率很高,可以达到50 MHz以上的拉比振荡频率.

基于自旋拉比振荡,可以方便地定义量子态的操控脉冲,它们对应着单比特的量子逻辑门[9,10].在布洛赫球面上,从|0⟩态到|1⟩态需要经历半个圆周,这样的微波脉冲为π脉冲,它等价于一个非门(NOT)的操作;|0⟩态到态需要经过1/4个圆周,称为π/2脉冲,对应着Hadamard门.

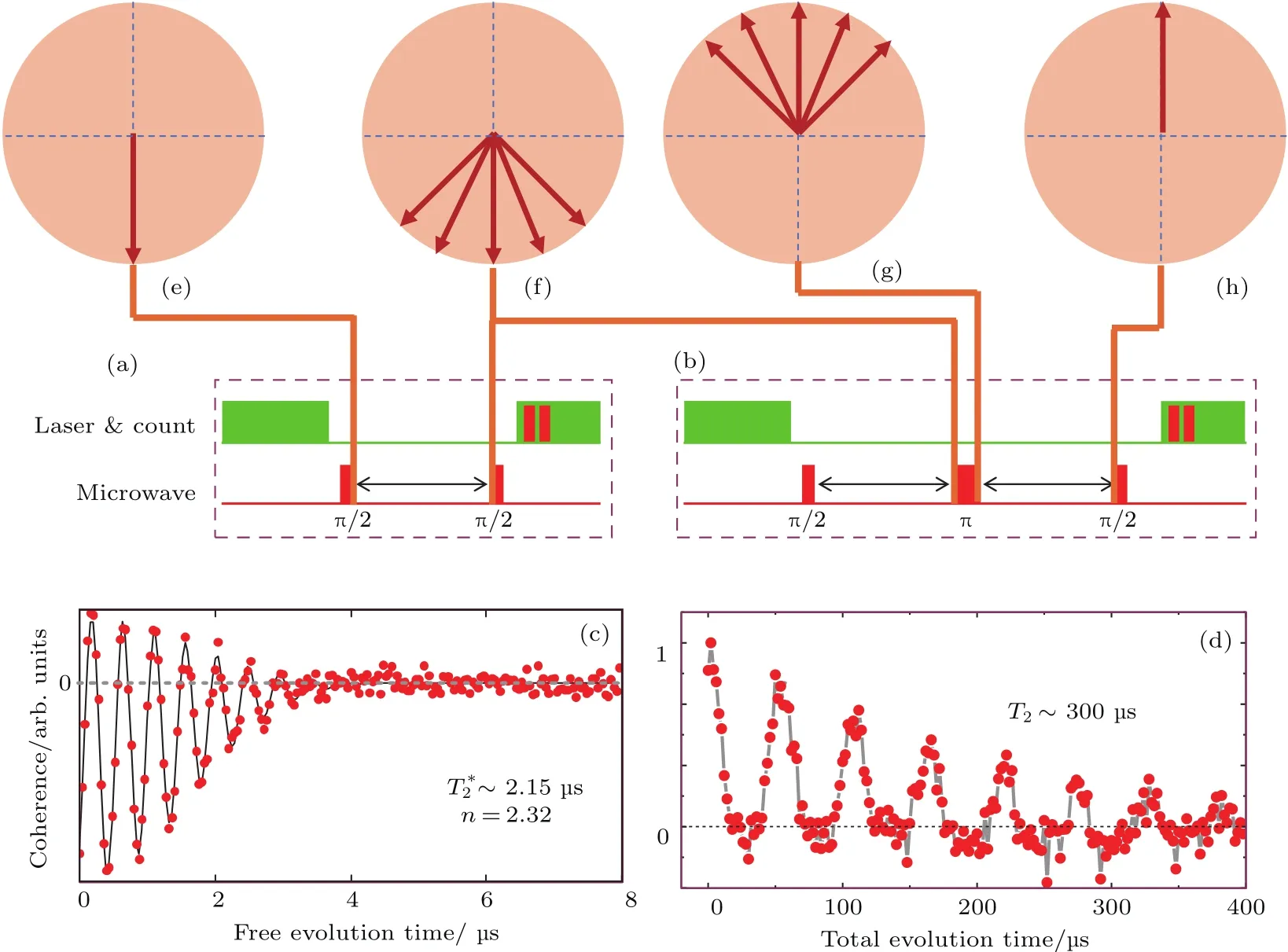
图5 自由弛豫衰减和自旋回波 (a),(b)脉冲序列;(c)典型的自由弛豫衰减和(d)自旋回波信号;(e)—(h)不同时刻叠加态相位演化在布洛赫球赤道面上的表示Fig.5.Free induction decay(FID)and Hahn echo:(a),(b)Pulse sequence;(c)typical FID and(d)Hahn echo signal;(e)–(h)phase evolution in the equatorial plane of Bloch sphere.

3.2 自旋量子态的相干性质

量子态包含着布居数和相位两方面的信息,在布洛赫球面上分别由z轴上的投影大小和赤道面内投影位置与x轴的夹角表示.对于一个真实存在的物理系统,它总是和周围环境存在着一定的耦合,量子态受到的影响也可以粗略地分为两类来讨论[1].引起电子自旋布居数变化的过程叫作纵向弛豫过程(relaxation),对应着自旋系统能量的变化,该过程的特征时间一般用T1来表示.对于NV中心自旋,T1通常由晶格热振动决定[21],室温下是毫秒量级.

引起量子态相位变化的过程叫做退相干

(dephasing或decoherence),一般用T2和表示.NV中心电子自旋的相干性质可以用自由弛豫衰减和自旋回波(T2)实验来测定.图5(a)和图5(b)分别是两种实验使用的脉冲序列,它们都从激光极化好的|0⟩态出发,用一个π/2脉冲把系统制备到叠加态然后让其自由演化一段时间.在此期间,自旋会绕着外磁场进动,进动频率取决于其所处局域磁场的大小.在自由演化过程中,自旋量子态会积累一个相位,大小等于进动角频率乘以演化时间.由于每次施加脉冲序列时NV中心所处的局域磁场不会严格一样(具体原因见下面的分析),多次测量的平均效果就是相位的不确定度会随着时间的增加而逐渐加大,直到完全丢失,该过程对应的特征时间就是也叫作退相干时间.图5(c)是典型的NV中心电子自旋自由弛豫衰减信号,对应的为2µs[18].

上面提到每次测量开始后,NV中心电子自旋所处环境的局域磁场都不能严格相同,主要原因是其近邻自旋所带来的影响.在金刚石晶格中随机分布着一些电子自旋(N原子,P1 center)和核自旋(主要是13C),它们构成了NV中心的自旋环境(spin bath).每个自旋相当于一个小磁铁,它们没有极化,测量开始时它们的状态是随机的,等效于给中心电子自旋施加了一个微弱但是每次都不太一样的磁场.由于这样一个机制的存在,实验测得的值其实由NV中心周围的自旋环境的统计性质决定.一般也将这个过程称为自旋环境热涨落带来的(中心电子自旋)退相干.对于室温和小磁场下的实验,周围自旋环境状态符合高斯分布,使得自由弛豫信号的外轮廓也表现出高斯形状的衰减,具体分析可以参考文献[18,22].

如果周围自旋环境是慢变的,电子自旋的相干时间可以用自旋回波技术来延长.如图5(b)所示的脉冲序列,在系统演化获得一个随机相位之后,可以施加一个π脉冲对其进行翻转.如果局域环境是不变的,那叠加态将会在接下来的时间中积累反向的相位,直到完全抵消掉前半段的相位,此时系统会恢复到刚制备好的无相位差状态.对于真实的系统,其自旋环境总是不可避免地在演化,所以自旋回波序列只能在一定程度上延长相干时间.对于高纯的金刚石样品,自旋环境主要由随机分布的13C核自旋组成,演化非常慢,所以用自旋回波可以获得几百微秒的自旋相干时间,如图5(d)所示.

表1列出了室温下不同金刚石样品中NV中心电子自旋的相干性质,可见样品纯净度越高,杂质自旋越少,自旋相干性质也越好.对于12C同位素纯化的化学气相沉积单晶金刚石,NV中心电子自旋在室温下都可以达到几百微秒,其中的13C核自旋相干时间更可以达到秒量级[23];更一般的情况是天然丰度的13C分布,此时一般是微秒量级,但是通过自旋回波等技术可以将其延长到几百微秒的T2相干时间.如果金刚石中氮杂质比较多,比如常见的Ib样品,那决定系统退相干的主要因素就是氮原子带来的P1中心,这是一种变化较快的电子自旋环境,对应的会降到微秒以下,自旋回波技术也只能略微延长其相干时间到微秒量级.进一步地,如果NV中心在比较靠近金刚石表面的位置,比如纳米颗粒中或者一些比较浅(深度小于50 nm)的样品中,其他磁性或者电荷噪音会进一步影响自旋相干性质[24].

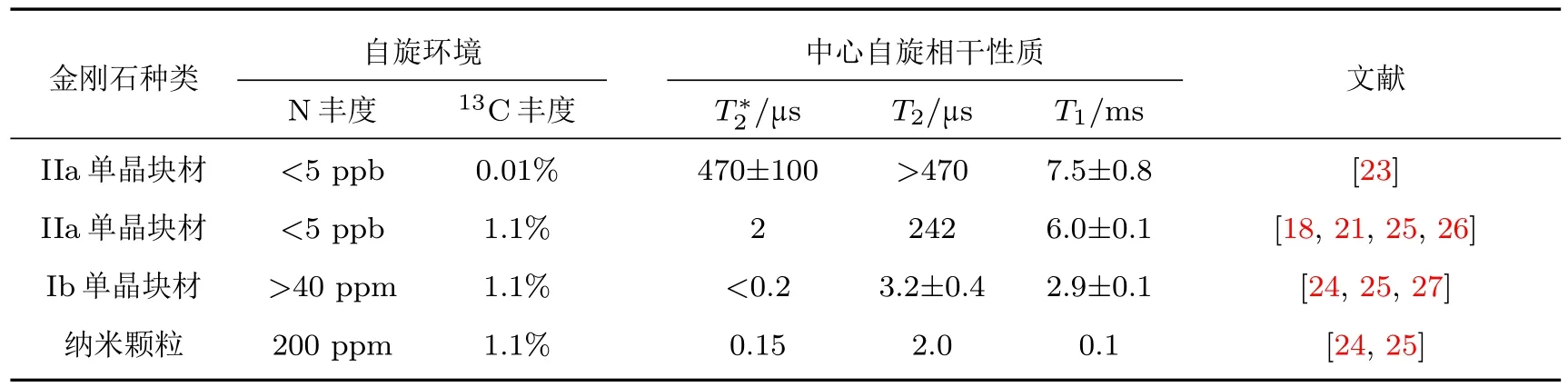
表1 室温下不同金刚石样品中NV自旋相干性质比较Table 1.Room temperature spin coherence of NV center in di ff erent diamond samples.

3.3 动力学解耦和动态核自旋极化

自旋量子态的相干时间是非常重要的参数,只有在相干时间之内,才能执行相干的量子操控.除了纯化样品的方式,还有一些动态方式可以延长自旋量子态相干时间,上面已经提到过的自旋回波技术就是其中的一种.通过翻转中心电子自旋,环境演化的慢变涨落会被抵消掉.进一步地,如果增加翻转脉冲的频率,则可以抵消更快的环境涨落,这种更普适的技术叫作动力学解耦.通常动力学解耦脉冲序列的设计要考虑自旋环境的动力学性质,还要尽量避免施加脉冲引入额外的操控误差[9,22].利用动力学解耦技术,可以将电子自旋的相干时间延长到接近T1的量级.

另外一种有效延长自旋态相干时间的方法叫动态核自旋极化,它主要是通过极化自旋环境来抑制其热涨落带来的非均匀展宽.相对于电子自旋,核自旋的旋磁比要小3个量级,这使得核自旋一般很难被极化起来.在NV中心相关的研究中,有两种动态核自旋极化的方案.其一是利用NV中心的激发态能级交错效应,在共振磁场(约500 G,1 G=10−4T)下,利用激光来同时建立电子自旋和核自旋的极化度[28].另外一种方案利用Hartman-Hahn双共振条件,让电子自旋拉比振荡的频率和近邻13C核自旋的进动频率一致,两者之间在spin-lock的脉冲作用下可以进行自旋极化度的交换.由于电子自旋的极化度可以在激光抽运下达到非常高,所以经过多次交换传递之后,周围的核自旋也逐渐被极化,自旋环境的非均匀展宽(热涨落带来)逐渐被抑制,在这种情况下电子自旋的相干时间T∗2可以获得数倍的延长[29,30].

4 自旋量子调控在量子计算和量子传感中的应用

量子传感是指利用量子系统(如囚禁离子、原子气、光子和自旋等),量子性质(如叠加态和纠缠态)或量子现象(如超导和玻色-爱因斯坦凝聚)对某一物理量进行精密测量的方法[12].作为室温下具有极好相干性质的固态自旋量子比特,NV中心是实现量子传感的绝佳物理系统,它同时拥有纳米尺度空间分辨率以及光学手段操控的便利,有望成为室温下单分子核磁共振谱仪以及核磁共振成像的核心单元.前面介绍了NV中心量子调控的基础理论,光磁共振实验技术以及NV中心自旋态的相干性质.在本节中,我们将进一步展示自旋量子调控在量子计算和量子传感中的具体应用,包括弱耦合核自旋的探测、电子自旋-核自旋复合系统受控量子逻辑门的实现、纠缠态的制备和在相位精密测量中应用以及磁性相变增强的纳米温度计的实现.

4.1 弱耦合核自旋量子态的单次读出

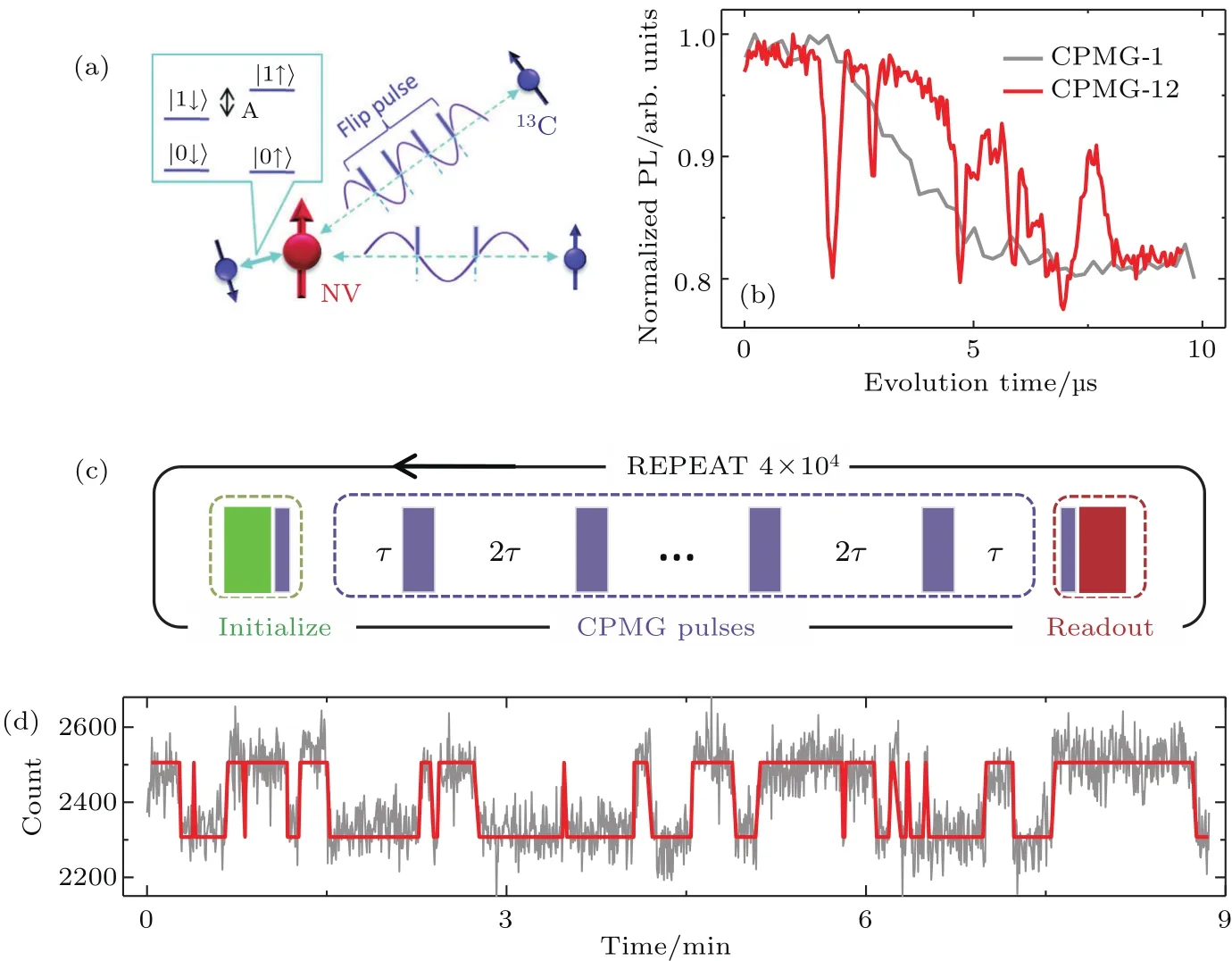
图6 弱耦合核自旋的探测和单次读出技术[31] (a)NV中心电子自旋和近邻13C核自旋的相互作用;(b)利用动力学解耦来解除自旋环境的影响或挑出特定的核自旋;(c)弱耦合核自旋单次读出脉冲序列;(d)核自旋的量子跳变信号Fig.6.Detection and single-shot readout of a weakly coupled13C nuclear spin[31]:(a)Interaction between an NV electron spin and nearby nuclear spins;(b)one nuclear spin can be picked up with Carr-Purcell-Meiboom-Gill(CPMG)sequence while others are decoupled;(c)pulse sequence for nuclear spin state single-shot readout;(d)quantum jumps signal.

单次读出技术是指对量子态的单次测量能以极高的保真度获得该原始态塌缩后的信息.测量理论告诉我们:对于一个自旋量子比特,在测量过程中它会按照一定的概率塌缩到其本征态,即自旋向上或者向下(取决于初态形式以及测量基的选择).以NV中心电子自旋读出过程为例,其单次读出技术要求在低温(4 K)下用共振光激发,而且要准确控制读出时间,才能从收集到的光子计数中以较高的置信度判断当前电子处于|0⟩还是|1⟩态[32].量子计算的实现需要数目众多的量子比特,NV中心近邻有数量众多且相干性质极好的弱耦合13C核自旋,如果能把它们利用起来,有望构建出功能强大的量子节点,成为量子网络和可拓展的量子计算核心器件.由于这些弱耦合的共振频率非常接近,很难实现只观测其中一个而不影响其他核自旋的状态,而室温下对弱耦合核自旋量子态的单次读出更是难上加难.已有的核自旋单次读出技术依赖于强磁场或低温等极端条件,而且只能施加在NV中心近邻的强耦合核自旋上[33,34].

动力学解耦脉冲和NV中心电子自旋的光学读出机制给我们提供了一种实现弱耦合核自旋单次读出的技术[31].如图6所示,核自旋与中心电子自旋的耦合强度取决于它们间的相对位置.通过调节动力学解耦脉冲的间隔,可以将特定的核自旋从复杂的自旋环境中选出.对于这个选出的核自旋,通过控制翻转脉冲的个数可以实现它和中心电子自旋之间强度可控的纠缠态制备.如果核自旋和电子自旋只是部分纠缠,那对电子自旋的投影测量等效于对核自旋的弱测量.通过持续施加这个脉冲序列,如图6(c)所示,核自旋的状态就会被锁定在两个特定的本征态上,从而用常规的非共振光学读出方法(室温)就可以实现弱耦合核自旋的单次读出[31].基于这种高灵敏度和高保真度的探测手段,处在复杂环境中的弱耦合13C核自旋量子状态跳变被成功观测到,如图6(d)所示.

4.2 动力学解耦实现的普适量子逻辑门

上面的例子展示了用动力学解耦脉冲实现的可控量子测量,我们也可以用它来驱动量子态的演化,实现量子逻辑门[35].如图7(a)所示,考虑一个近邻的13C核自旋,它的进动频率和方向同时受控于外加磁场以及电子自旋的状态;当电子自旋为|mS=0⟩态时,核自旋仅绕着外磁场进动;当电子自旋为|mS=1⟩时,核自旋的进动轴由外磁场和偶极相互作用的矢量合成决定.当我们给中心电子自旋施加动力学解耦脉冲时,电子自旋的状态会在|mS=0⟩和|mS=1⟩之间来回切换,核自旋的进动轴和进动速度也随之切换.在电子自旋和核自旋构成的双比特算符空间中考虑这个问题时,如图7(c)所示,动力学解耦脉冲会把系统导引到一个未知量子态,这是因为传统的动力学解耦脉冲仅以保护中心电子自旋相干性质为目标,并没有考虑核自旋量子态的演化.

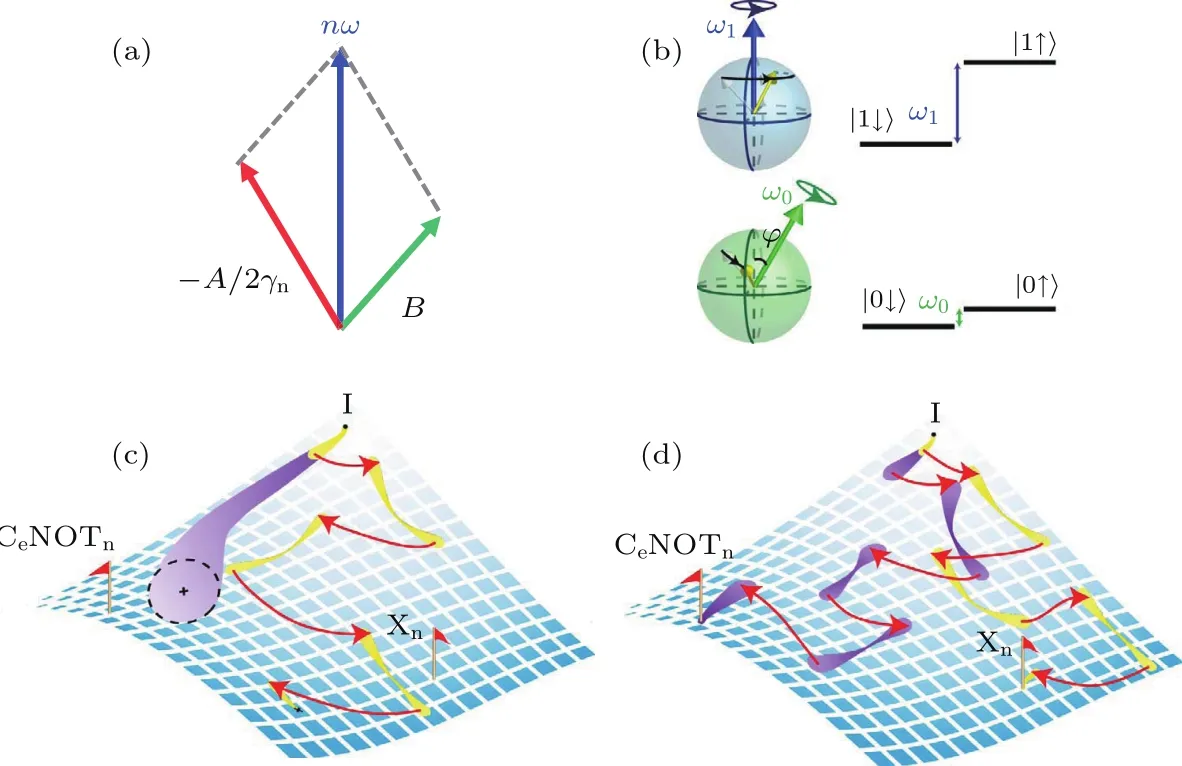
图7 用动力学解耦来驱动量子态的演化[35] (a),(b)外磁场和电子自旋状态共同影响核自旋的演化路径;(c)在算符空间中,如果不加任何操控,电子自旋态会很快退相干;施加普通动力学解耦会驱动量子态演化到不确定位置;(d)通过数值优化,可以让动力学解耦驱动效果等价于量子逻辑门操作,并保持系统相干性Fig.7.Quantum evolution steered by dynamical decoupling(DD)[35]:(a),(b)The evolution of a nearby nuclear spin is controlled by both the state of center electron spin and the external magnetic fi eld;(c)in the operator space,the electron spin dephase fast without DD protection;and the system is steered to an unknown state with traditional DD sequence;(d)with numerical optimization,the e ff ect of an engineered DD sequence equals to a quantum gate,which simultaneously protects the center electron spin from decohernece.

基于这个图像,一个值得探索的问题是能否在保护好中心电子自旋相干性质的同时,也把复合量子比特系统的演化进行可控的驱动,也就是实现量子逻辑门操作[35].答案是可行的:只要适当放宽传统脉冲的限制条件,针对具体耦合的核自旋(耦合参数实验测定),通过数值优化可以找到对应的动力学解耦脉冲序列,其驱动效果等价于两比特量子逻辑门操作.这样的量子逻辑门具有自保护功能,在操作的过程中可以主动消除环境噪音带来的相位噪声,对于量子计算的物理实现具有重要意义.实验上,我们用这种方法构建了NV中心电子自旋(用|0⟩和|1⟩表示)和近邻13C核自旋(用|↑⟩和|↓⟩表示)的受控非门(Ce-NOTn),并演示了从电子自旋的叠加态出发,利用这个受控非门制备复合体系最大纠缠态 贝尔态整个脉冲序列持续时间远大于中心电子自旋的退相干时间,但由于是用动力学解耦脉冲实现的量子逻辑门,电子自旋的相干性质得到了很好的保护,最终得到的贝尔态保真度达到91%[35].值得说明的是,该方案将动力学解耦从传统的仅延长量子态存储时间提升到驱动量子态演化的层面,具有普适意义.

4.3 纠缠加强的相位精密测量

纠缠是量子系统的独特之处,它非常脆弱敏感,如果操控得当的话,可以大大提高一些测量的精度.上面的实验中我们演示了最大纠缠态的制备,在本小节中,我们将展示纠缠态对于相位测量的加强效果[36].这里的相位是指量子态的相位信息,从上面关于退相干的讨论可知,大部分物理参数的测量(如弱磁探测、引力波探测、中微子振荡探测)最终都是对量子相位的测量.

量子纠缠可以有效提高相位测量的精度,如图8所示,当两个量子比特纠缠到一起时,对它们相位信息的统一测量能获得比独立测量更高的精确度,逼近海森伯极限.基于NV中心电子自旋和近邻13C核自旋构成的双量子比特系统,在实现了纠缠态相位制备和测量等关键实验技术之后[36−38],我们对比了相位信息的单独测量和纠缠态统一测量结果,统计这两种情况下相位测量的方差信息,发现通过量子纠缠可以明显地提升相位测量精度,从而实现了室温固态系统中量子计量学的原理演示.量子计量学有广阔的实用化前景,应用范围可以从微观世界到宏观物体甚至到宇宙星体,固态系统的原理性实验演示可以促进精密测量技术从经典方法到量子技术的跨越.

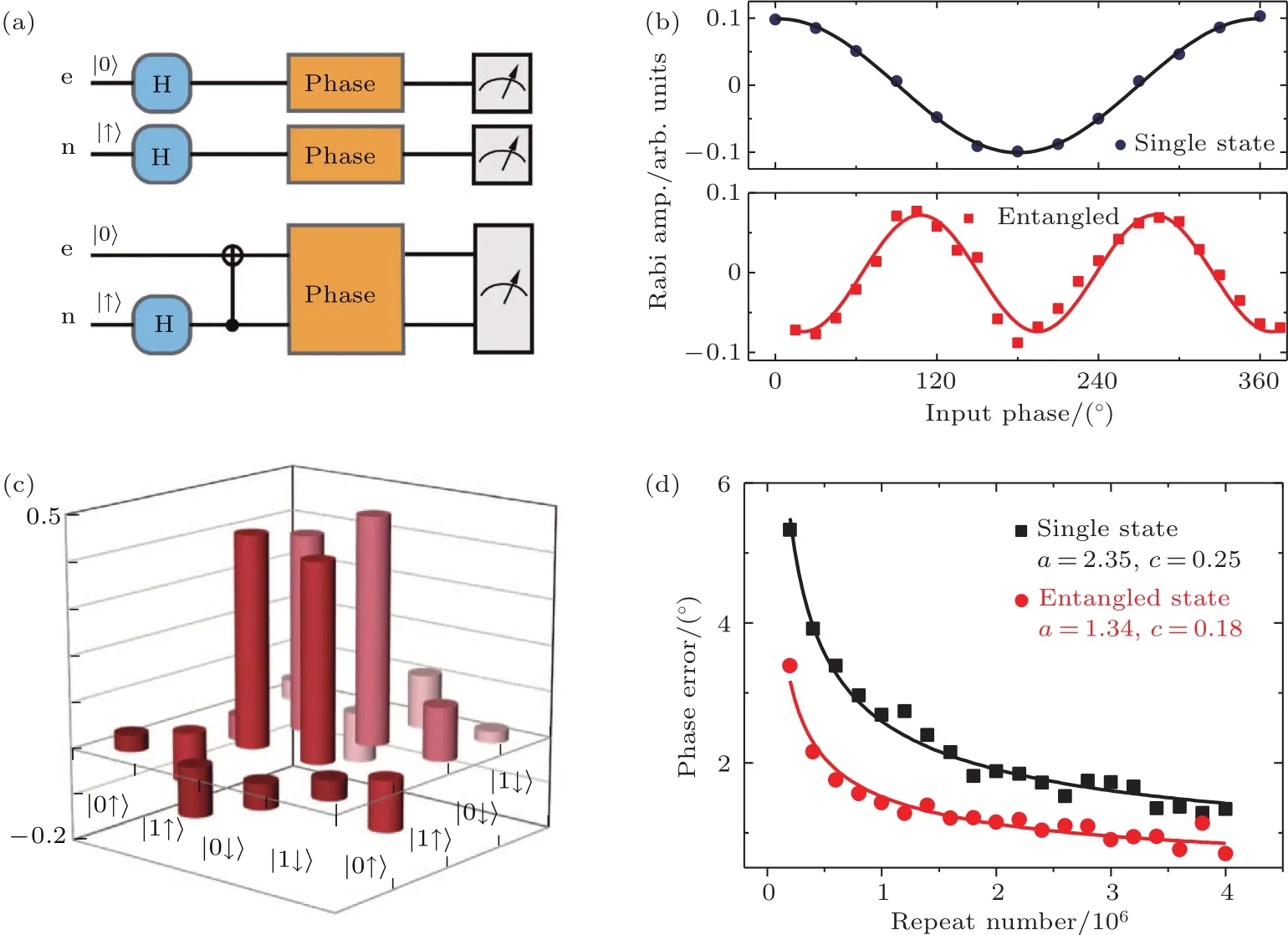
图8 纠缠加强的相位精密测量[36] (a),(b)原理示意图和相位依赖关系,其中上(下)部对应独立态(纠缠态);(c)贝尔态的相干层析结果;(d)纠缠态和独立态对相位测量的精度的影响Fig.8.Phase estimation enhanced by quantum entanglement[36]:(a)Quantum circuits and(b)phase relations,and the upper(lower)pane is single(entangled)state;(c)state tomography of the Bell state;(d)phase estimation error from single or entangled states.

4.4 纳米尺度量子传感器

NV中心电子自旋对所处环境的磁场信息非常敏感,通过对其光磁共振频率的测量,可以实现高灵敏度的磁场探测.但是作为一个量子传感器,它对温度和压强等参数的响应却比较微弱.为了拓展NV中心量子传感的实用性,我们提出并实验实现了一种磁性临界现象(相变)增强的纳米尺度温度探测方案[39].如图9所示,一颗纳米金刚石和磁性纳米颗粒(此处为CuNi合金)组成了这个复合传感器.利用纳米颗粒磁性随温度变化的规律,将其感受到的温度信息转化成磁场信息,然后用NV中心光探磁共振方法进行测量.由于NV中心对磁性信号非常敏感,原始的温度信号在转化成磁性信号之后,探测灵敏度大大提升;更进一步,在磁性纳米颗粒的居里温度(相变点)附近,其磁性和温度的依赖关系也变得非常灵敏,使得待测信号得到两个数量级的放大.

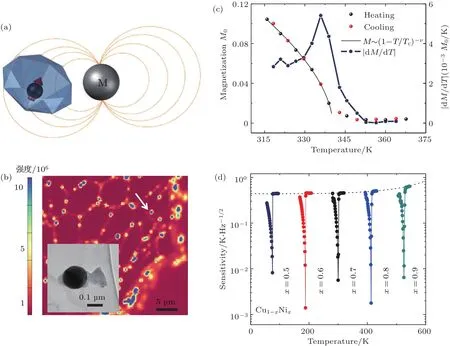
图9 磁性相变加强的纳米温度计[39] (a)复合温度计由纳米钻石和磁性纳米颗粒构成;(b)荧光扫描图(插图为扫描电子显微镜图);(c)单颗磁性纳米颗粒的相变;(d)复合纳米温度计的灵敏度和最佳工作区间Fig.9.Magnetic criticality enhanced nanothermometer[39]:(a)The hybrid sensor is built by a nanodiamond with ensemble NV centers and a magnetic nanoparticle(MNP);(b)confocal and scanning electron microscope(inset)images of the hybrid sensor;(c)phase transition of a single MNP;(d)temperature sensitivity and dynamic range of the hybrid nanothermometer.

图9(b)是实验合成的一个复合纳米温度计的扫描电子显微镜图和共聚焦荧光扫描图.利用原位的激光加热技术,我们系统地测试了该磁性纳米颗粒的磁性随着温度的依赖关系,并首次在室温下大气环境中观测到了单个纳米颗粒的磁性相变现象(铁磁态到顺磁态).如图9(c)所示,纳米颗粒的磁性在居里温度附近出现极大的变化.利用这个效应来进行温度测量,可以达到量级的灵敏度,是目前室温大气环境最灵敏的纳米温度计.通过选择不同居里温度的磁性纳米颗粒,可以改变复合传感器的最佳工作区间,以该实验中的CuNi合金为例,只要调节两种合金的比例,其相变温度可以在0—627 K(Ni的居里温度)之间连续调节.相应地,在这个温度区间范围内,针对不同的应用需求,都可以用磁性相变加强的原理制备灵敏的复合纳米温度计.该实验中合成的复合温度计的最佳工作区间选择在37◦C附近,特别适用于细胞内纳米尺度的温度探测.

5 结 论

本文从实验研究的角度,系统介绍了金刚石NV中心自旋光磁共振的基本原理和相关技术,重点讨论了其自旋退相干的主要机理和实验表征方法.以该领域最新的实验结果为例,探讨了单自旋量子调控技术在量子计算和量子传感中的一些具体应用.

经过近20年的积累和发展,NV中心自旋的量子调控技术已经相对成熟,尤其对单自旋的操控已经非常完善,目前的重点研究方向是发展多量子比特的相干操控技术,这也是所有量子计算实验研究的共同目标.NV中心邻近的弱耦合核自旋是实现较多量子比特的选择之一,而NV中心电子自旋和光量子比特或超导量子比特构成的复合系统也颇具吸引力,最近取得了一系列突破[40,41].

另一方面,将已经成熟的量子相干操控技术用于解决具体的问题,如纳米尺度的弱信号探测,也是大家重点关注的方向.对于生物、化学、材料和凝聚态物理领域的研究,纳米尺度极高灵敏度的传感器都具有良好的应用潜力[12,13,42].为了适应这些方面的应用,NV中心量子传感研究逐渐从金刚石体内扩展到体外,也从固态常温常压条件扩展到液态和复杂流体环境(如活细胞内),甚至包括极低温、高压和强磁场等极端条件.金刚石独特的力学、热学和光学性质,加上不断发展的量子操控技术,为这个领域提供了无限多的可能性.

[1]Ladd T D,Jelezko F,La fl amme R,Nakamura Y,Monroe C,O’Brien J L 2010 Nature 464 45

[2]Feynman R P 1982 Int.J.Theor.Phys.21 467

[3]Shor P W 1994 SIAM J.Comput.26 1484

[4]Grover L K 1997 Phys.Rev.Lett.79 325

[5]Dobrovitski V V,Fuchs G D,Falk A L,Santori C,Awschalom D D 2013 Annu.Rev.Condens.Matter Phys.4 23

[6]RondinL,TetienneJP,HingantT,RochJF,Maletinsky P,Jacques V 2014 Reports Prog.Phys.77 056503

[7]Doherty M W,Manson N B,Delaney P,Jelezko F,Wrachtrup J,Hollenberg L C L 2013 Phys.Rep.528 1

[8]Childress L,Hanson R 2013 MRS Bull.38 134

[9]Li J,Cui J Y,Yang X D,Luo Z H,Pan J,Yu Q,Li Z K,Peng X H,Du J F 2015 Acta Phys.Sin.64 167601(in Chinese)[李俊,崔江煜,杨晓东,罗智煌,潘健,余琦,李兆凯,彭新华,杜江峰2015物理学报64 167601]

[10]Liu G Q,Pan X Y 2018 Chin.Phys.B 27 020304

[11]Chen M,Meng C,Zhang Q,Duan C K,Shi F,Du J F 2017 Natl.Sci.Rev.DOI:101093/nsr/nwx121

[12]Degen C L,Reinhard F,Cappellaro P 2017 Rev.Mod.Phys.89 035002

[13]Schirhagl R,Chang K,Loretz M,Degen C L 2014 Annu.Rev.Phys.Chem.65 83

[14]Beha K,Batalov A,Manson N B,Bratschitsch R,Leitenstorfer A 2012 Phys.Rev.Lett.109 097404

[15]Gruber A,Drabenstedt A,Tietz C,Fleury L,Wrachtrup J,von Borczyskowski C 1997 Science 276 2012

[16]Liu Y,Kong F,Shi F,Du J 2016 Sci.Bull.61 1132

[17]Dréau A,Lesik M,Rondin L,Spinicelli P,Arcizet O,Roch J F,Jacques V 2011 Phys.Rev.B 84 195204

[18]Liu G Q,Pan X Y,Jiang Z F,Zhao N,Liu R B 2012 Sci.Rep.2 432

[19]Marseglia L,Hadden J P,Stanley-Clarke A C et al.2011 Appl.Phys.Lett.98 133107

[20]Jiang Q,Liu D,Liu G,Chang Y,Li W,Pan X,Gu C 2014 J.Appl.Phys.116 044308

[21]Jarmola A,Acosta V M,Jensen K,Chemerisov S,Budker D 2012 Phys.Rev.Lett.108 197601

[22]Zhao N,Ho S W,Liu R B 2012 Phys.Rev.B 85 115303

[23]Maurer P C,Kucsko G,Latta C,Jiang L,Yao N Y,Bennett S D,Pastawski F,Hunger D,Chisholm N,Markham M,Twitchen D J,Cirac I,Lukin M D 2012 Science 336 1283

[24]Liu D Q,Liu G Q,Chang Y C,Pan X Y 2014 Physica B 432 84

[25]Naydenov B,Dolde F,Hall L T,Shin C,Fedder H,Hollenberg L C L,Jelezko F,Wrachtrup J 2011 Phys.Rev.B 83 081201

[26]Childress L,Dutt M V G,Taylor J M,Zibrov A S,Jelezko F,Wrachtrup J,Hemmer P R,Lukin M D 2006 Science 314 281

[27]Hanson R,Dobrovitski V V,Feiguin A E,Gywat O,Awschalom D D 2008 Science 320 352

[28]Jacques V,Neumann P,Beck J,Markham M,Twitchen D,Meijer J,Kaiser F,Balasubramanian G,Jelezko F,Wrachtrup J 2009 Phys.Rev.Lett.102 057403

[29]Liu G Q,Jiang Q Q,Chang Y C,Liu D Q,Li W X,Gu C Z,Po H C,Zhang W X,Zhao N,Pan X Y 2014 Nanoscale 6 10134

[30]London P,Scheuer J,Cai J M,Schwarz I,Retzker A,Plenio M B,Katagiri M,Teraji T,Koizumi S,Isoya J,Fischer R,McGuinness L P,Naydenov B,Jelezko F 2013 Phys.Rev.Lett.111 067601

[31]Liu G Q,Xing J,Ma W L,Wang P,Li C H,Po H C,Zhang Y R,Fan H,Liu R B,Pan X Y 2017 Phys.Rev.Lett.118 150504

[32]Robledo L,Childress L,Bernien H,Hensen B,Alkemade P F A,Hanson R 2011 Nature 477 574

[33]Neumann P,Beck J,Steiner M,Rempp F,Fedder H,Hemmer P R,Wrachtrup J,Jelezko F 2010 Science 329 542

[34]Dréau A,Spinicelli P,Maze J R,Roch J F,Jacques V 2013 Phys.Rev.Lett.110 060502

[35]Liu G Q,Po H C,Du J F,Liu R B,Pan X Y 2013 Nat.Commun.4 2254

[36]Liu G Q,Zhang Y R,Chang Y C,Yue J D,Fan H,Pan X Y 2015 Nat.Commun.6 6726

[37]Pan X Y,Liu G Q,Yang L L,Fan H 2011 Appl.Phys.Lett.99 051113

[38]Chang Y C,Liu G Q,Liu D Q,Fan H,Pan X Y 2013 Sci.Rep.3 1498

[39]Wang N,Liu G Q,Leong W H,Zeng H L,Feng X,Li S H,Dolde F,Fedder H,Wrachtrup J,Cui X D,Yang S,Li Q,Liu R B 2018 Phys.Rev.X 8 011042

[40]Zhu X,Saito S,Kemp A,Kakuyanagi K,Karimoto S,Nakano H,Munro W J,Tokura Y,Everitt M S,Nemoto K,Kasu M 2011 Nature 478 221

[41]Hensen B,Bernien H,Dréau A E,Reiserer A,Kalb N,Blok M S,Ruitenberg J,Vermeulen R F L,Schouten R N,Abellán C,Amaya W,Pruneri V,Mitchell M W,Markham M,Twitchen D J,Elkouss D,Wehner S,Taminiau T H,Hanson R 2015 Nature 526 682

[42]Casola F,van der Sar T,Yacoby A 2018 Nat.Rev.Mater.3 17088