高性能反谐振空芯光纤导光机理与实验制作研究进展∗

丁伟 汪滢莹 高寿飞 洪奕峰 王璞

1)(中国科学院物理研究所,北京 100190)

2)(北京工业大学激光工程研究院,北京 100124)

(2018年4月18日收到;2018年4月27日收到修改稿)

1 引 言

20世纪,石英光纤技术的出现和广泛应用奠定了光纤通信、光纤激光器、光纤传感三大领域的革命性成就[1].光纤技术是当今工业文明的重要基石.21世纪,随着信息传输容量的持续性爆炸式增长、光纤激光器功率/脉宽的不断提升以及极端环境下大规模阵列传感的应用牵引,石英作为光纤材料的本征缺陷(非线性、色散、光致损伤、紫外中红外不通光等)暴露得越来越明显,对上述工业领域的继续发展造成了严重制约.空芯光纤领域的先驱者们正是怀着一个“突破实心光纤本征瓶颈”的梦想开始了对全新导光机理的探索研究——在空气纤芯中建立起导光通路,可以完美地解决光纤技术中遇到的本征的材料缺陷[2].

从传统的全内反射导光机理的角度来看[3],在空气芯中实现导光是一件非常奇怪的事情.构造全内反射条件需要将折射率更低的包层材料包裹在纤芯周围.但是自然界中并不存在比空气折射率更低的介质材料.金属材料可以有小于1的折射率(实部),但是由于本征的自由电子振荡造成的等离子体损耗,它并不适合在光波段制作光波导[4].因此,似乎唯一的解决办法就是采用微纳尺寸的人造结构来设计并制作出特定波长、特定入射角下的等效的低折射率材料来充当光纤包层[5].人们最先想到的就是将不同的介质材料进行周期性排列来实现并优化类似布拉格反射的光场相干相消[6−8].由此设计出来的空芯光纤称为二维光子带隙光纤[9]和全向光子带隙光纤(又称全向带隙布拉格光纤)[10].在结构上,它们分别拥有光纤横截面内的非连续的二维平移对称性和一维径向平移对称性.理论上,由于光子带隙提供了一个光波态密度严格为零的区域,基于光子带隙原理的空芯光纤可以做到限制损耗无限小.随着光纤包层层数的增加,光的泄漏可以降低到零,实现真正的光波导模.但是,上述理论忽视了一个重要的前提条件,光纤中不同介质区域中的波矢纵向分量必须保持恒定不变.然而,事实上微结构光纤的每一个玻璃表面上都本征性地存在着粗糙不平的所谓的表面毛细波,它会造成上述波矢纵向分量守恒的条件失效,引入一种称之为表面散射的基础损耗[11].从另一个角度来看,表面毛细波的普遍存在使得光子带隙中的光波态密度不再严格为零,存在着一个去不掉的本底!既然如此,是否还有必要继续坚持微结构光纤中严格的结构平移对称性呢?另外一个源于表面毛细波现象的重要启示是,任何一种高性能的空芯光纤必须有效降低模场与玻璃表面的空间重叠.基于这两方面的考虑,学术界逐渐将空芯光纤导光机理的研究转向了另一种更强调在局域范围内实现光场相干相消的方式,也就是所谓的反谐振式空芯导光[11−13].相较于光子带隙的导光方式,这种导光方式可以实现更宽带但是以泄漏模为特征的导光.

对光子带隙导光机理的研究已经发展了二十余年,许多综述性论文和专著对此进行了清晰的阐述[6,14,15].对于光子带隙光纤,人们可以利用布洛赫边条件计算出无限延伸的周期性晶格中的光子能带和带隙[16],也可以运用超晶格平面波展开法[17]、有限元法[18]、多极矩法[19]、有限差分法[20]等数值方法来计算实际光纤中的纤芯模式.数值计算的优点是精确度高,但是它无法给出直观的物理图像.拿光子晶格和固体物理中的晶体概念相类比[6,21],可以给出一些简单的诸如“更高折射率的玻璃相当于更低的原子势阱”这样的图像,对解释和设计空芯光纤光学性能的帮助并不直接.对于布拉格光纤,由于其内在的结构简单性(对称性),解析计算变得非常简单,人们可以直观地解释光纤模场的分布情况并以此为基础对光纤性能进行调节[21,22].但是,由于实际加工中的局限性(主要是由材料损耗带来的问题),布拉格空芯光纤的损耗[23]远大于光子带隙空芯光纤(三个数量级以上),这降低了研究这类空芯光纤导光机制的学术意义.

相较而言,对反谐振式空芯导光机理的研究长期被忽视,主要原因是它无法实现严格的光导模,而是以泄漏模的方式进行导光.然而,随着近年来高性能反谐振空芯光纤的传输损耗逐步接近光子带隙空芯光纤的损耗记录(1620 nm波长下1.7 dB/km)[24],清晰地阐明反谐振空芯光纤的导光机理变得越来越迫切和重要.一旦在传输损耗这个指标上超越了光子带隙空芯光纤,反谐振空芯光纤在其他性能上的优势(如宽带导光和高损伤阈值等)将触发光纤光学研究和应用领域的一场革命.

本文以我们团队过去几年在导光机制理论和实验加工方面的研究工作为基础,系统论述并展示反谐振空芯光纤基础性能的最新研究进展.在第2节中,针对单壁包层反谐振空芯光纤发明了一套基于格林积分公式[25,26]的半解析计算方法,首次揭示了反谐振空芯光纤中的结构可调性的物理基础;在第3节中,针对一类由互相不接触的玻璃管围绕形成的反谐振空芯光纤,将包层划分为几个介质层,清晰地指出了四个影响光纤限制损耗的物理效应和它们各自的强度[27],展示了从紫外到中红外波段的反谐振空芯光纤的加工制作[28−31];在第4节中,对反谐振空芯光纤中的保偏性质进行了基础性的研究[32]和初步的加工制作[28];在第5节中,对反谐振空芯光纤在弯曲条件下的通光性能进行了理论阐述和实验测量[30];最后,对反谐振空芯光纤基础研究和应用前景进行了总结和展望.

2 单壁包层反谐振空芯光纤的半解析计算模型

从光学构造的角度来看,我们发现反谐振空芯光纤似乎介于光子带隙空芯光纤和布拉格光纤之间.反谐振空芯光纤以单一的熔石英为基础材料,避免了布拉格光纤中聚合物或者软玻璃带来的材料吸收损耗和材料内部密度涨落造成的散射损耗.与光子带隙空芯光纤[23,33]相比,反谐振空芯光纤对光场分布的操控更加直接.前者的包层一般由6—10层结构组成,后者的包层则只有2—3层玻璃壁.反谐振空芯光纤中的模场分布相干相消主要发生在短距离内(比如一层玻璃壁相对的两个界面之间),这与布拉格光纤的情况类似.但是,反谐振空芯光纤包层中的能流分布并没有只局限在光纤径向方向,这又与光子带隙空芯光纤中的情况类似.认识到这一点对接下来发展的解析计算模型非常重要.因为意识到了反谐振空芯光纤导光机理的复杂程度介于光子带隙空芯光纤和布拉格光纤之间,我们确定了将影响导光过程的短程干涉效应和长程叠加效应区分开来处理.在这个数学处理过程中,我们发展了一种半解析的计算方法.

为了突出反谐振空芯光纤的上述结构特征,我们选择了单壁包层的简单结构,短程的模场干涉只发生在一层玻璃壁的两边,而远场辐射的叠加则发生在玻璃壁以外的区域.我们只讨论光纤的基模.

2.1 平板波导中的泄漏模

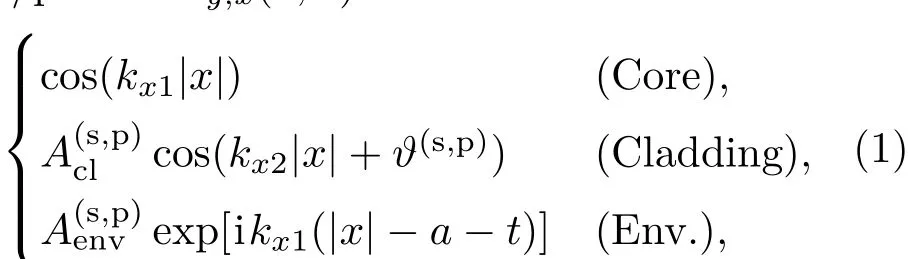
一维平板波导中的泄漏模可以表示为[34]s/p-Pol.:Ey,x(z,x)=eiβz×其中,纵向(z方向)传播常数β=neff·k0(k0为真空波矢,neff为模式的有效折射率),横向波矢kxj=(n2j−n2eff)1/2·k0.如图1所示,对两个偏振模式(s和p),包层壁外侧处的电场相位值都锁定在了某个固定值上(见图1(c)).这一点事实上可以从边条件连续和小角度入射(即|kx2|≫|kx1|)推导出来.

泄漏模的传输损耗表示为α[dB/m]=8.69k0·Im(neff).我们发现,将包层壁外侧位置的电场振幅取出来,利用能量守恒定理,可以推导出泄漏模的传输损耗:

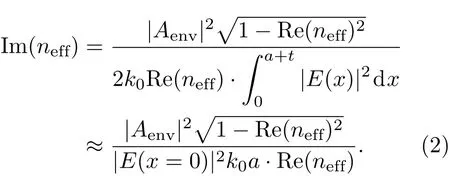
假设|Ey,x|≫ |Ez|,并令基模的横向波矢满足Re(kx1)≈π/2a.利用数值计算结果我们检验了这个公式的精确性.这也意味着平板波导泄漏模特定位置处的电场强度包含着模式衰减的信息.利用这一点,可以大大简化数学处理.

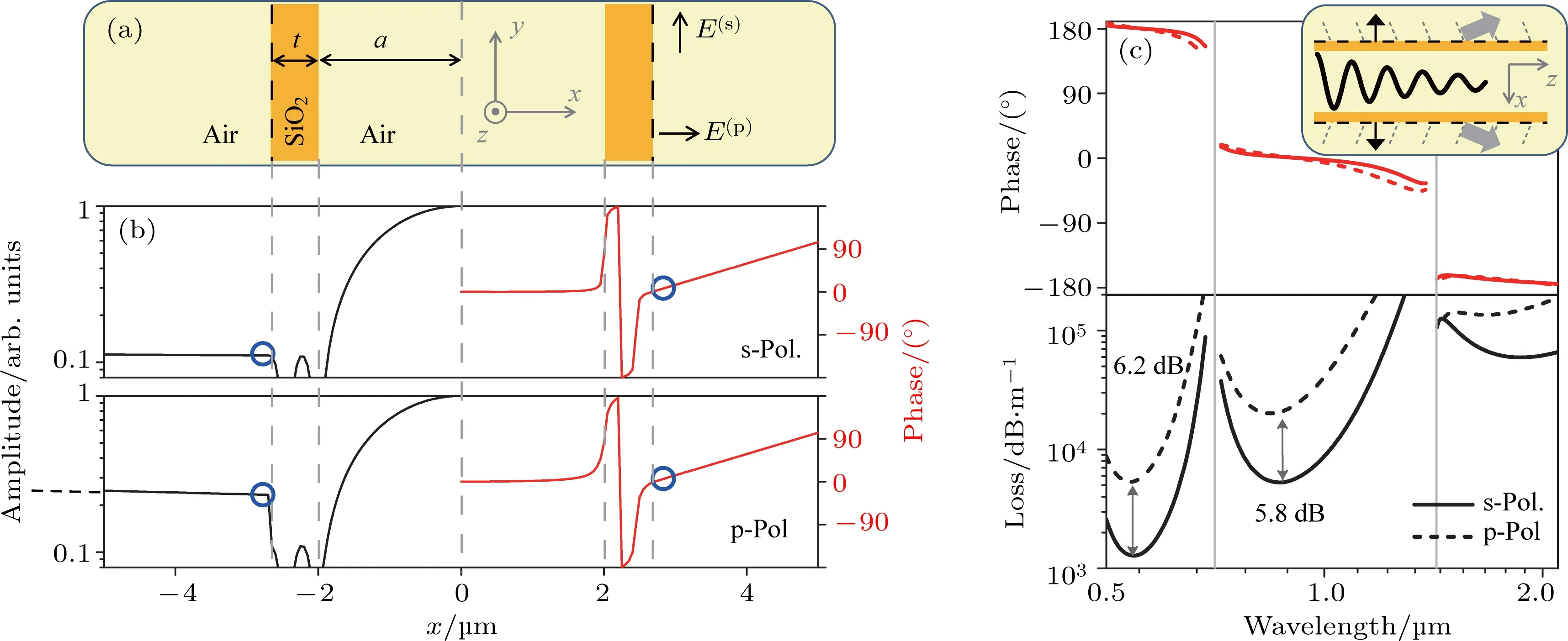
图1 (a)M型平板波导示意图;(b)s偏振和p偏振模式中电场分量的振幅(对数尺度)和相位分布图(分别为Ey和Ex),a=2µm,t=0.67µm,λ=0.938µm,石英折射率为1.45;(c)纤芯基模的最外边界处电场相位(虚线)和损耗谱[25]Fig.1.(a)Schematic illustration of a one-dimensional three-layer slab waveguide;(b)distributions of the amplitude(logarithmic scale)and phase of the major electric fi eld components in the s-and p-polarizations(Eyand Ex,respectively);a=2 µm,t=0.67 µm,and λ =0.938 µm;(c)phase of the electric fi eld at the outermost boundary(see the dashed lines in the insert)and loss spectra of the fundamental core mode[25].

2.2 对光纤二维结构的近似处理

为了降低光纤结构的复杂度,继续做了一个近似处理,将不同轴向角方向(φ)的玻璃壁等价为一个平板波导.如图2(a)所示,几何变换后产生的平板波导具有半径的空气芯子,同时偏振角度也需要进行修正.这里的参数是人为加入的参数.

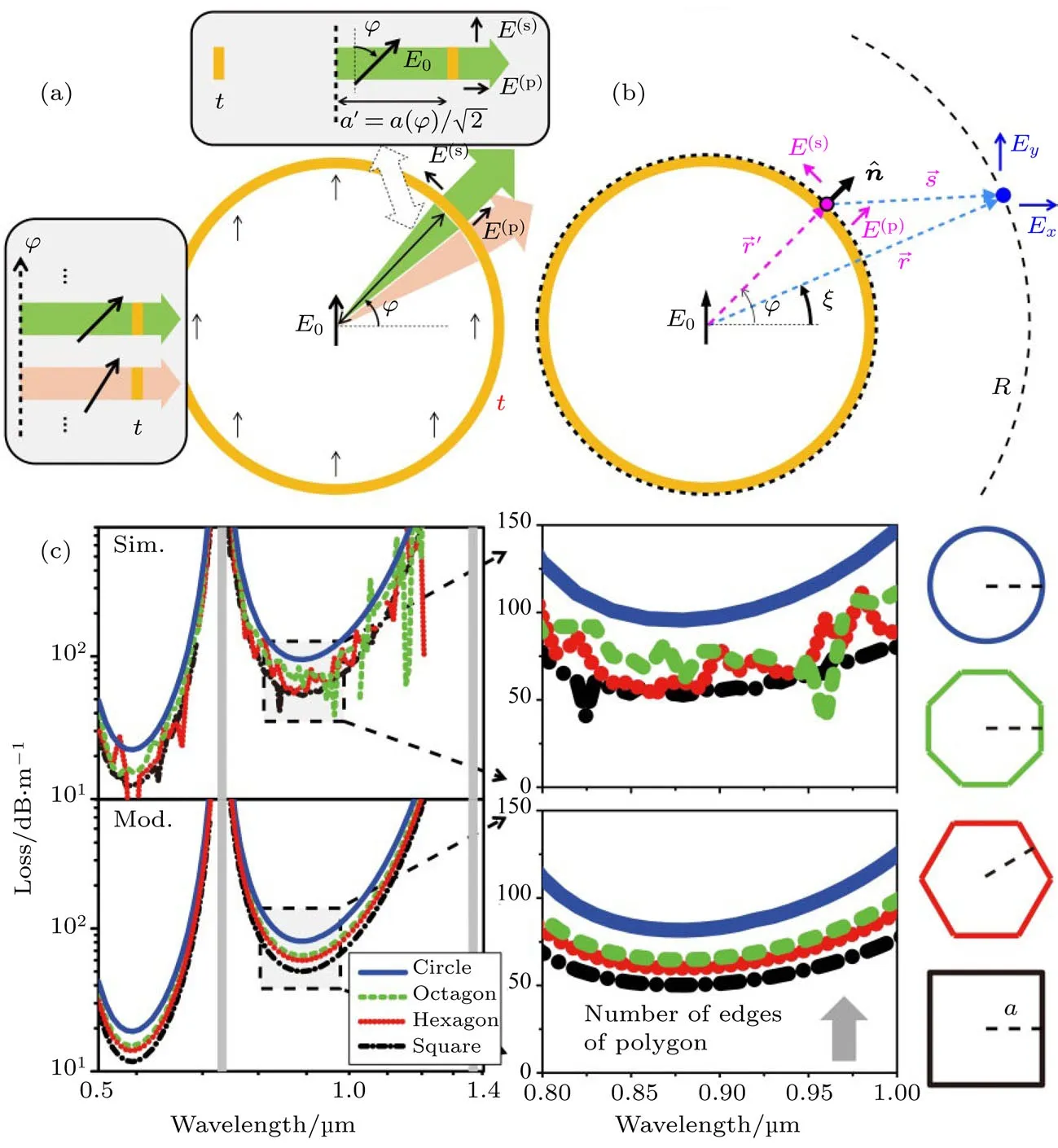
图2 (a)从单层圆形反谐振空芯光纤到平板波导的几何变换过程示意图;(b)运用格林函数积分方法计算远场电场强度的示意图;(c)仿真计算和模型计算得到的单壁包层圆形(实线)、八边形(虚线)、六边形(点线)、方形(点划线)反谐振空芯光纤限制损耗谱;a=9.76µm,t=0.67µm[26]Fig.2.(a)Geometry transformation from a circular single-wall hollow-core anti-resonant fi ber to a series of slab waveguides,and the polarization directions are denoted by the arrows;(b)evaluation of the electric fi elds in the far- fi eld region(R)by using the Green’s function and integrating along a closed loop;(c)numerically simulated and semi-analytically modeled loss spectra of the single-wall circular(solid line),octagon(dashed line),hexagon(dottedline),and square(dash-dotted line) fi ber with a=9.76µm and t=0.67µm[26].

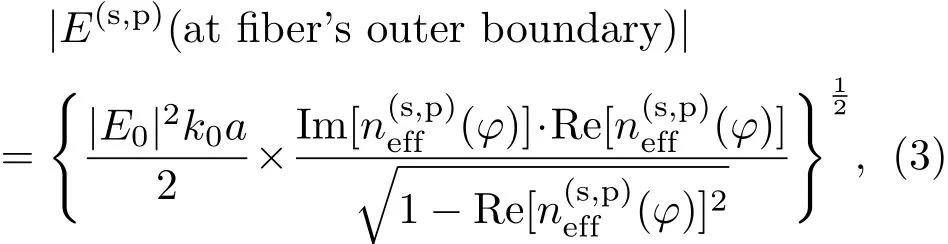
而这个位置电场的相位值锁定在某一个常数上,再加上对光场的s和p偏振态的比例分解(振幅比cosφ/sinφ),从而获得了电场的全部物理信息.

从上面的简化处理中,可以快速得到光纤模式整体的有效折射率和光纤中空气区域的横向波矢分量

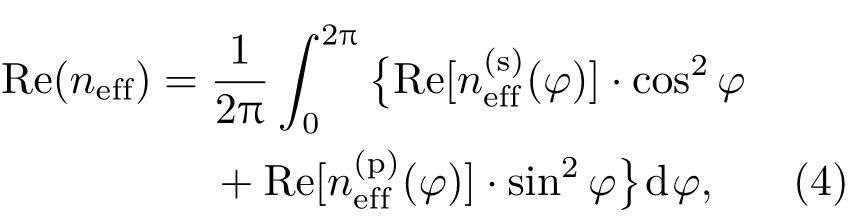
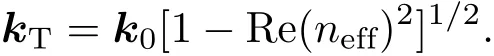
如2.1节所述,在一维平板波导中快速计算得到泄漏模的有效折射率之后,可以通过(2)式得到玻璃壁外侧处的电场振幅:

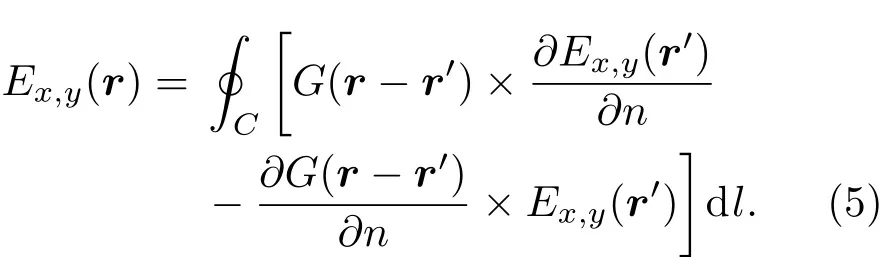
然后,如图2(b)所示,利用光纤最外层区域中的二维标量亥姆霍兹方程,和格林积分定理,电场在远场位置处的分布可以表示为

玻璃壁的外侧边界将作为积分的闭合回路,它的向外法线方向定义为n.格林函数

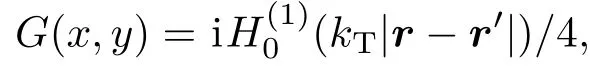
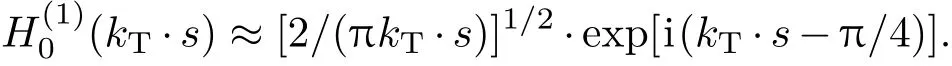
当距离趋近于无穷时渐近形式为在一阶近似情况下,利用积分路径为等相面的条件,∂Ex,y/∂n≈ ikTEx,y.最终(5)式可以近似表达为

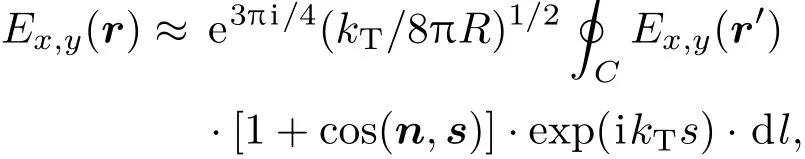
其中的[1+cos(n,s)]/2为惠更斯-菲涅耳原理中的基尔霍夫倾斜因子.

继续简化处理,并利用能量守恒定律,可以得到半解析计算公式:

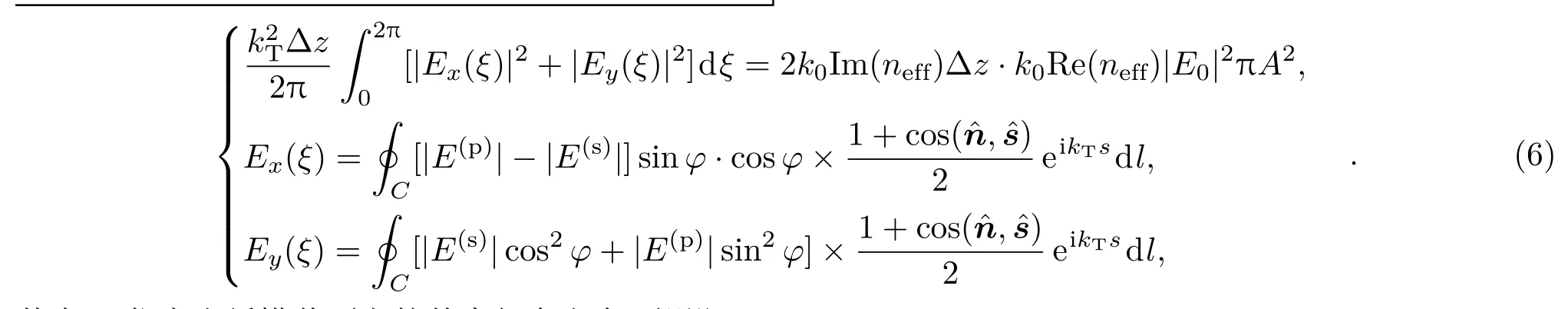
其中,ξ代表光纤横截面上的某个径向方向.假设kTa≈π/2,

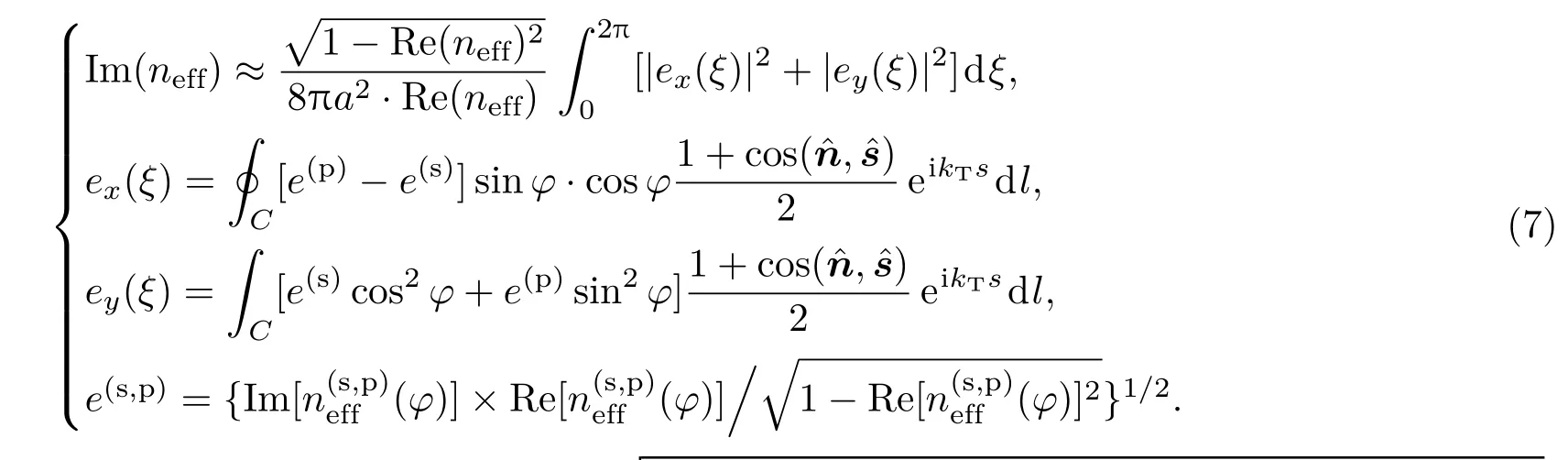
上述公式对不同结构、不同尺寸的光纤在不同波长上都表现出了极高的计算精度.图4(c)对比了不同形状的单壁反谐振空芯光纤的限制损耗谱.我们第一次清晰地指出了源于光纤玻璃壁形状的结构可调性.我们的半解析计算模型得到了与数值仿真完全一致的结论:当玻璃壁形状从圆形变化到内摆线形,限制损耗呈现逐渐减小的趋势!

以上述工作为起点,我们进行了一系列逐渐深入的探索研究.比较直接的一项是对(6)式中的基尔霍夫倾斜因子的改进.对近似表达式∂Ex,y/∂n ≈ ikTEx,y, 用更精确的∂Ex,y/∂n ≈(∂Ex,y/∂x)·sinθ−(∂Ex,y/∂y)·cosθ进行了替换.定义积分路径的法线方向为n=sinθ·x−cosθ·y.∂Ex,y/∂x和∂Ex,y/∂y可以从麦克斯韦方程组

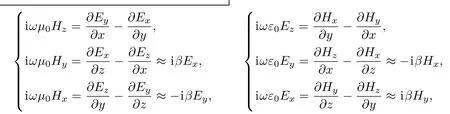
和玻璃壁外侧相位锁定效应(∂Ex,y/∂x)·cosθ+(∂Ex,y/∂y)·sinθ≈ 0中推导出来.由此,我们得到

方程(6)被修正为

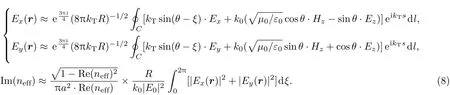
新的公式可以适用于更高弧度的反谐振空芯光纤结构.

3 负曲率空芯光纤的理论建模和实验拉制

在第2节中,我们证实了反谐振空芯光纤存在着由玻璃壁形状造成的结构可调谐性,并且进行了解析计算.为了把我们的分析扩展到实际的光纤结构中去,必须考虑更复杂包层结构的光纤.近年来,一类由一圈互相不接触的玻璃管围绕空气芯构建起来的反谐振空芯光纤结构正在快速成为空芯光纤领域的研究焦点[30,35−37].数千米长度的[38]或者通光窗口覆盖整个可见光波段的[29]这种类型的反谐振空芯光纤已经得到了实验展示.本文称这类光纤为负曲率空芯光纤.

在这一节中,我们将阐明决定负曲率空芯光纤限制损耗的各种来源并对它们进行量化分析.我们把包层中的玻璃管人为地切割成两半,对整个光纤结构进行逐层分析,并与布拉格空芯光纤的结果进行对比[27].最后,列出了在我们实验室中实现的各种参数的负曲率空芯光纤.

3.1 玻璃壁上的掠入射和法布里-珀罗干涉

在一层玻璃和空气界面上,可以使用斯涅耳定律和菲涅耳方程来描述光的反射和折射(图3(a)):sinϕ=n·sinΘ,

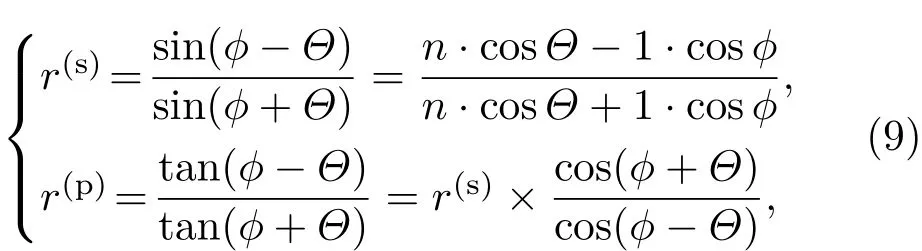
其中,ϕ(Θ)为入射(折射)角,r为振幅反射率,s(p)代表偏振.通过改变入射角,可以调节反射率接近1.也就是说,原则上一层玻璃-空气界面足以实现理想的“镜面反射”.但是,实际情况是降低掠入射角(ϕ→π/2)会导致严重的弯曲损耗.因此,可行的解决办法是构造一个级联的玻璃界面结构,使得透射光可以指数式地衰减下去(图3(b)).如果暂时忽略反射光的作用,可以将透射光功率表示为

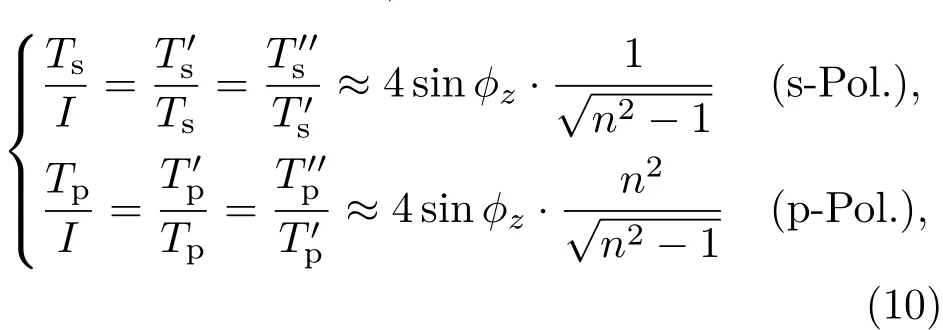
其中,ϕz(Θz)是掠入射(入射)角的补角,Ts,p=1−|r(s,p)|2.可以用(10)式对图1(c)中两个偏振模的损耗谱进行检验.当存在两个玻璃界面时(单壁包层平板波导),p偏振模式中光的泄漏速度是s偏振模式的n2N=4.4倍(∼6.45 dB).图1(c)的两个通光窗口中,两个偏振模的损耗差分别为6.2 dB和5.8 dB.两者符合得很好.

我们可以来检查一下布拉格空芯光纤中的情况.由于这类光纤的包层使用了至少两种不同的玻璃,加上空气介质一共有三种不同的材料,无法做到每个包层界面上的掠入射角都非常小.在大多数界面上反射率其实并不高,无法真正发挥上面说的“级联式玻璃界面”对抑制泄漏损耗的效能.反之,如果保留纯石英的玻璃壁构架,把光纤中的空气统一替换成某一折射率的液体,即便两者的折射率差别不大(比方说∆n=0.01),也可以通过调节掠入射角使包层中的每一个界面上的反射率都非常高,充分利用“级联式玻璃界面”的好处.关于这一性质的实验展示和应用,可以参考我们最近在空芯光纤中进行的生化传感工作[39].

把上述“级联玻璃界面”的概念拓展到光纤结构中去,需要采用子午线光束假设.也就是说,对基模(HE11)这样的混合偏振模式,每一块玻璃界面上的入射光包含了同等份量的s偏振和p偏振光.如果我们可以近似假设一个级联玻璃表面彼此平行的情景,总的透射率可以表示为

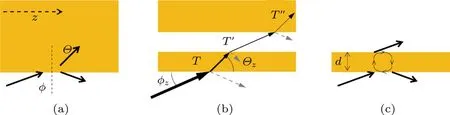
图3 (a)单个玻璃界面、(b)一连串玻璃空气界面和(c)标准具结构上发生的光的透射和反射[27]Fig.3.Schematic illustration of light re fl ection/refraction at(a)a glass:air interface,(b)a series of glass interfaces,and(c)an etalon structure[27].

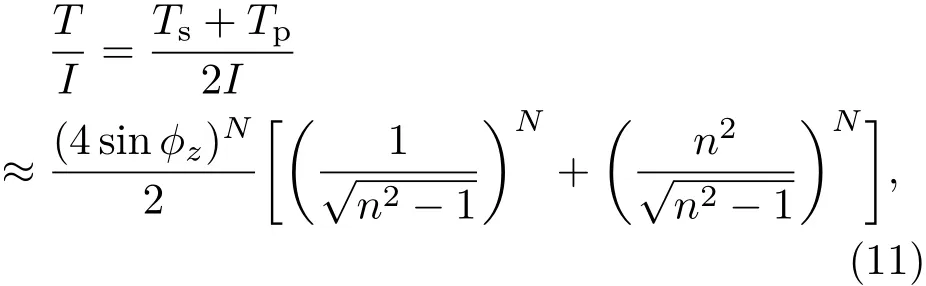
其中,N代表玻璃界面的数量.如果我们把玻璃折射率n视作变量,透射率是折射率n的函数.当N=1,2,3,4,5时,透射率的最小值出现在折射率∼(1+21/5)1/2时.我们发现这些值与熔石英的实际折射率相当接近.由于光纤混合模中包含了同等份量的s偏振和p偏振光,使用过高或者过低折射率的玻璃材料会造成反谐振空芯光纤更多的以p或者s偏振成分向外界泄漏能量.石英玻璃的折射率是两种情况的折中.

如图3(c)所示,当两个平行界面构成一个标准具,法布里-珀罗干涉使得透射率和反射率变成

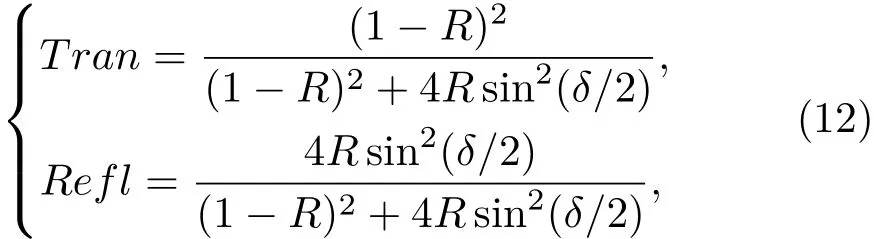
其中,R=|r|2,δ=ncosΘ ·k0·2d代表相移积累量.当δ=(2m+1)π(m为整数)时,反谐振条件成立,标准具可以抑制光的透射.在掠入射条件下,R≈1,方程(12)简化为Tran≈(1−R)2/[4sin2(δ/2)].除了上文提到的透射系数级联(1−R)2之外,相干相消作用可以额外降低透射率四倍之多.

接下来将注意力转到多层同心圆光纤的结构中去(图4).利用矩阵计算方法[21],这种光纤的限制损耗可以精确地获得.我们将光纤中的损耗用毛细管中的损耗系数进行归一化,引入只量化反映反谐振空芯光纤中的干涉效应的好处因子,

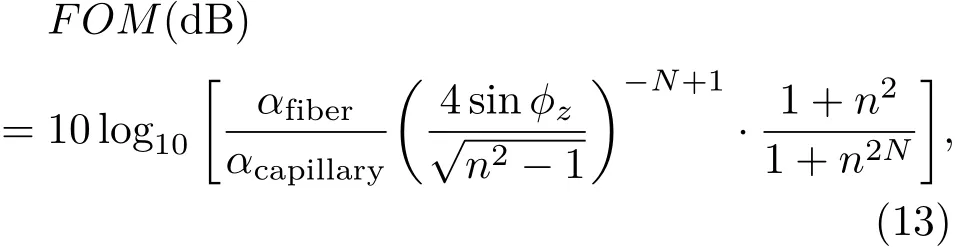
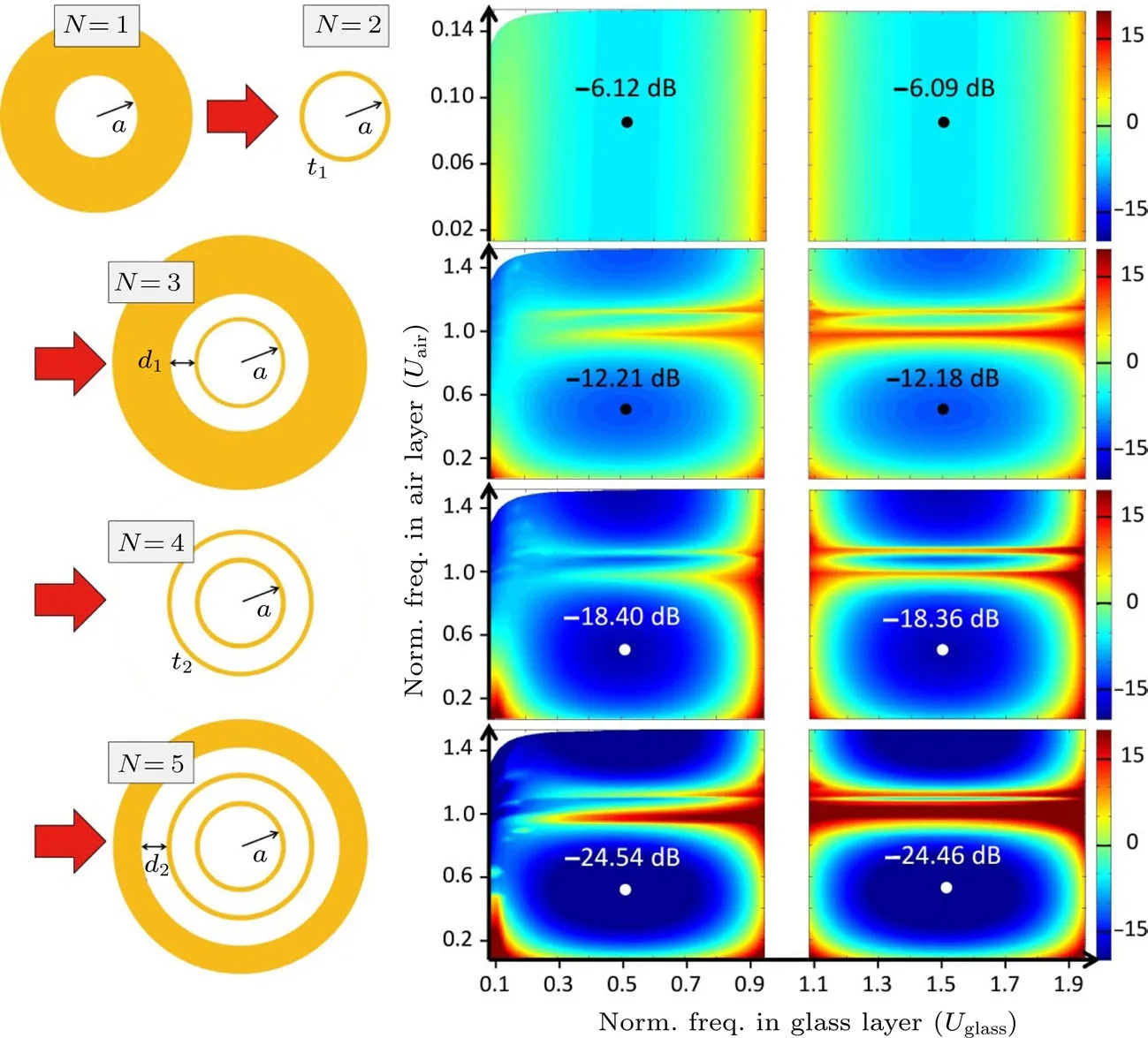
图4 反谐振干涉效应的好处因子随玻璃和空气介质层的归一化频率(Uglass和Uair)变化的函数,图中第一行的y轴定义为2[1−Re(neff)2]1/2/λ[27]Fig.4.Figure-of-merit(FOM)of anti-resonant re fl ecting optical waveguide interference e ff ect as a function of the normalized frequencies of the glass and air layers(Uglassand Uair).In the fi rst row,the y-axis is de fi ned as 2[1−Re(neff)2]1/2/λ[27].

空芯光纤和毛细管的芯径需要保持相同,sinϕz可以通过[1−Re(neff)2]1/2来近似地获得.另外,我们又引入了两个归一化频率参量Uglass=2ti[n2−Re(neff)2]1/2/λ和Uair=2di[1−Re(neff)2]1/2/λ来表征玻璃壁和空气层中的相位积累作用.FOM可以视为Uglass和Uair的函数.这样,我们就在一定程度上避免了介质层中的结构细节引入的复杂性.相较于人们经常使用的归一化频率(F=2ti[n2−1]1/2/λ),所引入的Uglass和Uair加入了掠入射角的因素,把空气层和玻璃壁对光能泄漏的影响一视同仁.一旦纤芯半径(a)和空气层厚度(di)的比例固定了,对光纤基模而言,Uair对任何波长的光都近似为常数,这可以从Marcatili-Schmeltzer近似公式[22]Re(neff)≈ [1−(u01λ/2πa)2]1/2中推导出来.这种波长不敏感性并不存在于Uglass中,因此解释了为什么反谐振导光效应最早与包层结构中的玻璃壁厚度联系在了一起,而忽视了包层空气同样具有帮助反谐振导光的能力.

在图4中,玻璃壁和空气层的厚度(ti和di)分别设为0.24µm和10µm,纤芯的直径和波长可以变化.N>2时,反谐振导光效应开始出现.在谐振区域(Uglass,air=1,2,···)附近导光效应遭到了破坏,而在反谐振区域导光效应得到了加强.我们还发现,这种源于光场干涉的导光辅助效应可以在玻璃层和空气层之间累加起来,每一层介质都至多提供约6 dB的损耗抑制.

3.2 逐层分解计算模型和光纤限制损耗的近似公式

对于一个负曲率空芯光纤,需要研究前面提到的效应是否已经涵盖了光纤的所有导光机理.如图5所示,我们对光纤的包层结构延径向方向进行了逐层分解.每个玻璃管都被剖开成负曲率的一半和正曲率的另一半,它们构成了两个玻璃壁层,具有相同的厚度和不同的形状.玻璃管包围起来的空气部分构成了一个结构复杂的空气介质层,它的有效厚度有待确定.假设反映反谐振效应的FOM 指标仍然是Uglass和Uair的函数.根据Marcatili-Schmeltzer近似公式[22],当只考虑一个空气圆管的基模时,可以用u01代替Uair定义式中的这里代表空气圆管的直径,u01是零阶贝塞尔函数的第一个零点.

图5 在N=1,2,3,4条件下的(a)同心圆空芯光纤和(b)负曲率空芯光纤的损耗谱;t=0.24µm,2a=30µm,d=10 µm,2a′=28.66 µm,d′=16 µm[27]Fig.5.Calculated and simulated loss spectra of(a)the annular fi ber and(b)the hollow-core negative curvature fi ber with the number of interfaces N=1,2,3,4,respectively.The geometric parameters are:t=0.24µm,2a=30 µm,d=10 µm,2a′=28.66 µm,and d′=16 µm[27].

在图5中,对比圆环形和负曲率形空芯光纤两种结构,它们的纤芯直径分别为2a=30µm和2a′=28.66 µm,玻璃壁厚度(ti)为0.24 µm,前者的空气层厚度(di)为10µm,后者的玻璃管直径和管间距离分别为16µm和0.8µm.这样的尺寸设计可以保证在波长520—1500 nm范围内模式折射率之差∆Re(neff)<2×10−6.同时,圆环形光纤中的空气层厚度正好是负曲率形光纤空气孔直径的π/2u01倍.根据数值计算的结果,当N=1时,两种光纤的损耗谱都是平滑曲线,并且处于相同量级(800 nm处50—400 dB/m).当N=2时,两种光纤都有一层玻璃壁包层,它们的损耗谱中都出现了一个反谐振通光窗口520 nm—+∞.对圆环形光纤而言,损耗下降了14.1 dB.根据3.1节的分析,其中的8 dB来自于增加一层玻璃界面造成的菲涅耳反射,6 dB来自于玻璃层的反谐振效应.对于负曲率光纤而言,损耗下降了22.8 dB.很显然,玻璃壁的形状产生了约8.7 dB的降低损耗的好处.当N=3时,对两种光纤而言,损耗谱都发生了向下平移(14.4 dB和14.3 dB,约8 dB来自于增加一层玻璃界面,约6 dB来自于空气层中的反谐振效应).下文中将讨论为什么损耗抑制效应没有表现出对空气层形状的依赖性.当N=4时,圆环形光纤和负曲率空芯光纤又产生了13.6 dB和17.5 dB的损耗抑制.我们再次观察到了玻璃壁形状对损耗抑制造成的影响.可以看到,除了证明的负曲率玻璃壁形状,正曲率玻璃壁形状也能有效降低损耗.

图6对玻璃壁形状这一因素进行了更加直接的分析.可以看到在反谐振空芯光纤的玻璃壁最外侧,实际上形成了一个等相位面.以此为闭合回路,利用格林积分公式可以推导出远场辐射强度,从而估算出整根光纤的能量泄漏情况.图6中的三种不同形状的玻璃壁(圆形、负曲率形和正曲率形)对远场泄漏的效果是不同的.从圆形等相面上辐射出去的光束可以“聚焦”在“无穷远点”上,而“无穷远点”是整个系统唯一的一个“泄漏点”.从(正/负)曲率形等相面上辐射出去的光束在“无穷远点”这个“泄漏点”上其实是“失焦”的.这就解释了玻璃壁形状对光纤损耗可以有如此大调节作用的原因.

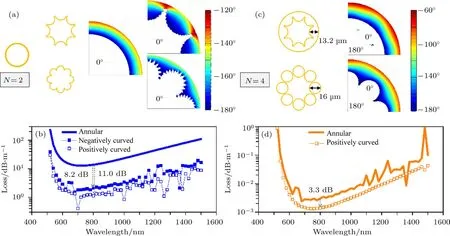
图6 (a),(c)针对不同光纤结构仿真得到的电场相位分布图以及(b),(d)限制损耗谱 (a)颜色标定的范围为−180◦到−120◦,纤芯区域的相位是0◦;(c)颜色标定的范围为−180◦到−60◦,纤芯区域的相位是0◦和180◦;(b),(d)计算的所有光纤具有相同的有效这折射率[27]Fig.6.(a),(c)Simulated phase pro fi les of the electric fi elds of di ff erent fi ber structures and(b),(d)the corresponding con fi nement loss spectra.In(a),the color bar ranges from −180◦ to −120◦,and the phases in the core areas are 0◦.In(c),the color bar ranges from −180◦ to −60◦,and the phases in the core areas are 0◦ and 180◦,respectively.One can see that the phase contours of−180◦ (marked in dark black)exactly at the outermost boundaries of the glass walls.Note that,in(b)and(d),all the fi bers have the same modal indices(data not shown)[27].

需要强调的是,仅在环境介质为空气时,光纤横截面上的二维亥姆霍兹方程中的kT=k0[1−Re(neff)2]1/2≈u01/a. 通过闭合回路上的格林积分可以得到显著相干相消的结果.类似的情况在图6(c)中也会发生(包层里有两层玻璃壁和一层空气).但是由于最外层玻璃壁的尺寸大于纤芯直径,积分结果中得到的相干相消的程度将弱许多(图6(d)中正曲率玻璃壁相较于圆环形玻璃壁的损耗仅仅下降了3 dB).当光纤最外围的介质变成二氧化硅时,上述二维亥姆霍兹方程将改为KT=k0[n2−Re(neff)2]1/2≫kT.通过闭合回路上的格林积分得到的相位值(正比于KT)在数量级上将远大于π,将导致相位干涉作用被平滑掉.这也解释了图5中N=1,3的情况,也就是为什么空气层的形状对光纤限制损耗没有结构可调谐性.

把以上所有分析集中起来,可以给出涵盖全部导光效应的负曲率形空芯光纤的限制损耗,

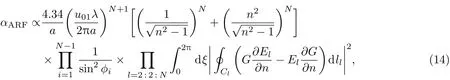
其中,毛细管中的模式限制损耗为αcapillary≈8.69[u01λ/(2πa)]2(1+n2)/[2a(n2−1)1/2],sinϕz≈Uglass,air为第i层介质上的相位积累,闭合积分路径(Cl)为玻璃壁外侧边界,ξ代表远场辐射角.

当包层结构中的Fano共振现象[40]对光纤限制损耗的影响可以忽略不计时,也就是环绕着玻璃壁流动的光能显著弱于垂直于玻璃壁方向的能流时,可以将上述公式推广应用到其他反谐振空芯光纤中去.四种光学现象决定了光纤的限制(泄漏)损耗:1)光束相对于玻璃壁的掠入射;2)光束穿透一连串玻璃界面形成的级联式的菲涅耳透射;3)界面之间多次反射造成的干涉效应(反谐振效应,或者说叠加的法布里-珀罗效应);4)由玻璃壁形状决定的辐射波干涉效应.前两个效应发生在光束单向穿透包层的路径上,后两个效应发生在光的干涉叠加过程中,其中一个是在介质层的垂直方向上(短程干涉),另一个是在整个光纤横截面上(长程干涉).在这里,我们没有考虑光纤的弯曲损耗、散射损耗和吸收损耗.

3.3 覆盖紫外、可见光、近红外、中红外波段的反谐振空芯光纤拉制

我们团队在过去五年间成功研制了覆盖紫外到中红外波段的反谐振空芯光纤(图7).我们的光纤拉制技术保证了包层中的玻璃管结构均匀、壁厚足够薄、而且玻璃管相互不接触.这使我们成为国际上公认的为数不多的几家可以制作高性能反谐振空芯光纤的研究机构之一.国际上具有相同空芯光纤拉制水平的单位还有英国巴斯大学、法国利摩日大学、英国南安普顿大学、德国马普所、丹麦NKT公司、美国中弗罗里达大学以及美国OFS实验室.

在中红外波段,包括熔融石英在内的大多数材料具有严重的材料吸收,不适合直接拉制实芯中红外光纤.虽然硫化物和氟化物玻璃在中红外波段具有较低的材料吸收,将其拉制成的光纤具有较高的透光率,但是,这类光纤非线性系数大、损伤阈值低、制备技术难度大,并且机械稳定性和化学稳定性差,包括熔接在内的后处理技术不成熟.石英基的空芯光纤为中红外区域导光提供了新思路.我们拉制的一款工作在中红外光谱区域的低损耗宽带反谐振空芯光纤,实验测量得到的光纤传输通带从1.5µm延伸到4.5µm,光纤在2.45µm和3µm波长处的传输损耗分别为50 dB/km和130 dB/km.这款光纤可以实现中红外激光的柔性传输并保持很好的单模特性,在军事、工业和环境科学中具有潜在的重要应用[31].

在近红外波段,通过结构优化,将传输损耗降低到了8 dB/km@1µm水平[30],接近目前国际上的最低损耗值(7.7 dB/km@750 nm).目前我们正在继续改进结构设计降低传输损耗,并利用中心波长1064 nm、脉冲宽度17 ps、重复频率400 kHz的高功率超短脉冲激光对该光纤进行了超短脉冲激光传输实验,实现了74 W高功率传输,对应的单脉冲能量达到185µJ[41].

可见光波段传输的反谐振空芯光纤相比近红外波段光纤的拉制难度更大,对光纤的制备工艺、拉制技术要求更高,国际范围内仅有一两个课题组可以实现拉制,并且拉制成功的光纤普遍传输带宽较窄、损耗较大.我们在国际上首次实现了覆盖几乎整个可见光波段的反谐振空芯光纤,这得益于我们将包层毛细管壁厚降低到210 nm.实验测量到的传输损耗在532 nm仅为80 dB/km,是同波段所有已报道工作的最低记录.基带传输窗口从420 nm延伸到1600 nm.另外,还测试了该光纤在高功率超短脉冲激光下的传输特性,用中心波长532 nm的高平均功率激光器和高单脉冲能量激光器进行了超短脉冲传输测试,两台激光器的重复频率分别为58 MHz和1 kHz,脉宽分别为80 ps和20 ps,分别实现了32 W高平均功率和144µJ超短脉冲的传输实验,测得光纤损伤阈值为150µJ[29].另外,还观测到了空气中的多个气体拉曼散射谱线,包括只占空气成分0.4%的二氧化碳气体谱线,预示着空芯光纤在大气检测、气体传感中的重要应用潜力.

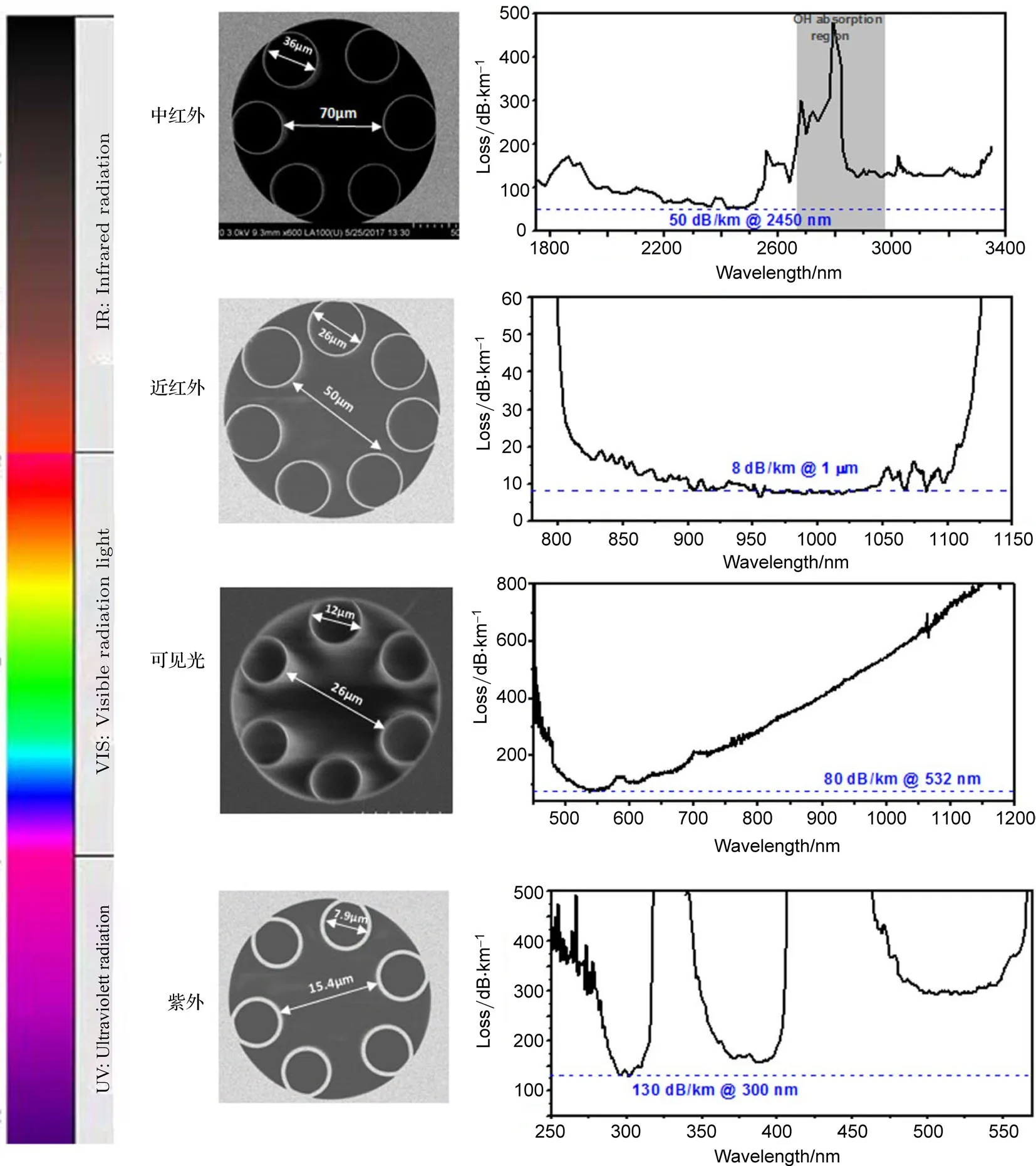
图7 本团队研制的从中红外到紫外光波段的反谐振空芯光纤Fig.7.Examples of hollow-core anti-resonant fi bers fabricated by our team.The working spectra cover from ultraviolet to mid-infrared.

在紫外波段,石英光纤存在着严重的本征缺陷——长时间辐照下的紫外光致暗化效应、可传导功率低以及多模传输.一根具有高损伤阈值和良好光束质量的紫外光纤,可以在紫外光源、离子阱操纵、光疗和荧光成像等应用中发挥重要的作用.显然,空芯光纤是紫外光传输的理想载体.近几年来,多个课题组做了相关尝试,报道了不同结构的紫外空芯光纤,但是损耗一直处在1 dB/m以上的水平,而且只能承受毫瓦量级的连续光.我们通过适当增大壁厚实现了窄谱带紫外导光,在300 nm处损耗达到0.13 dB/m,比之前的报道降低一个数量级.我们还首次实现了355 nm的高功率激光传输,当20 ps脉冲、峰值功率160µJ的激光耦合进光纤后,在8 h的监控时间内没有发现光学损伤,这是国际上首次报道紫外波段的高功率激光传输[28].

4 偏振保持反谐振空芯光纤的导光机理和初步制作

利用前文中提出的泄漏损耗的计算模型可以直观地指导反谐振空芯光纤中的偏振性能,这是所有数值计算方法无法做到的,属于一种逆向物理问题求解.偏振保持属性在大量光纤应用场景中都是不可或缺的.相较于实芯光纤而言,要实现空气芯子中的偏振保持面临很大挑战,因为任何与纤芯材料有关的光学效应都失效了.虽然在光子带隙空芯光纤中可以实现窄带的双折射效应[42,43],但是如何在宽带通光的反谐振空芯光纤中实现这一点仍然是一个空白.

4.1 混合型反谐振反射光波导导光窗口中的强双折射效应

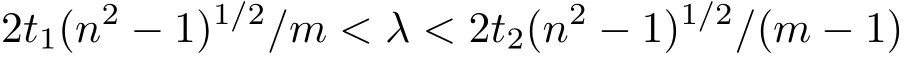
对正方形状的单壁包层反谐振空芯光纤进行了快速的半解析计算,两个偏振态下纤芯基模的有效折射率给出了光纤的双折射和偏振依赖损耗谱(图8(a)).当水平方向的玻璃壁厚t1=0.67µm、竖直方向的玻璃壁厚t2=0.54µm时,我们找到了两类不同属性的反谐振通光窗口.一类是普通意义的反谐振通光窗口,(m为整数),另一类我们称之为混合型反谐振通光窗口.例如,在218—265 THz频率范围内,t1=0.67µm对应m=2,t2=0.54µm则对应m=1.除了偶尔有一些Fano谐振造成的尖峰之外,半解析计算结果与数值仿真符合得很好(误差小于5%).可以看到,在正常的反谐振通光窗口内(174 THz)玻璃壁外侧将光场在相位锁定在一个确定值(−180◦),在混合型的反谐振通光窗口内(243 THz)不同厚度的玻璃壁外侧处相位被锁定在了不同的值(−180◦和0◦).

我们把∆nr=Re(nV−nH)和∆ni=Im(nV−nH)画出来,下标V和H分别代表竖直和水平偏振,上标r和i代表实部和虚部.根据Kramers-Kronig(K-K)关系[44],可以得到如下描述光纤双折射和偏振损耗之间关系的假设性公式:

图8 (a)方形单壁层反谐振空芯光纤基模两种偏振态的有效折射率和损耗谱,a1=a2=9.76µm,t1=0.67µm,t2=0.54µm;当频率等于(b)174 THz和(c)243 THz时,水平偏振模中Ex的振幅和相位分布图;(d)用简化模型计算的和(e)数值仿真计算的两种偏振下的有效折射率实部差(∆nr,黑色实线)和虚部差(∆ni,红色实线)[32]Fig.8.(a)Semi-analytically modeled loss and modal index spectra of a square-shaped single-wall hollow-core antiresonant fi ber(in the inset)at the two polarizations,a1=a2=9.76 µm,t1=0.67 µm,and t2=0.54 µm;at the horizontal polarization,the fi eld amplitude and phase distributions of Exare plotted at the frequencies of(b)174 THz and(c)243 THz respectively;(d)modeled and(e)simulated di ff erences of the real(∆nr,solid black lines)and imaginary(∆ni,solid gray lines)parts of the e ff ective modal indices between the two polarizations[32].

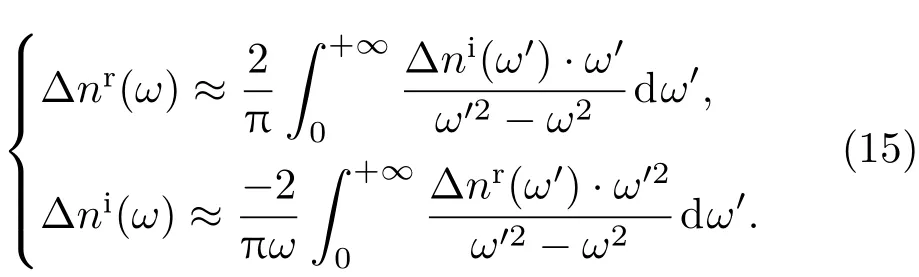
对上述K-K关系公式进行了检验,与数值计算结果符合得很好(图8(d)).我们在第一阶混合型反谐振通光窗口中发现了10−4量级的双折射,预示着在反谐振空芯光纤中同时实现了宽带传输和强双折射是可能的.这是一种不同于以往实芯光纤和光子带隙空芯光纤的双折射产生机制.我们第一次做到了利用K-K关系这样简洁的数学公式对反谐振空芯光纤中的某一个特性进行针对性的设计.此外,还从不同类型不同级数的反谐振条件对光纤模场大小的影响的角度分析了反谐振光纤的双折射特性,得到的结果与K-K关系的预测是一致的.

4.2 具有四阶旋转对称性的负曲率型反谐振空芯光纤制作

为了在实验上看到双折射效应,首先需要保证反谐振空芯光纤的结构具有四阶旋转对称性.我们对具有这一特征的负曲率型反谐振空芯光纤进行了尝试加工[28].在这样的结构中,纤芯模式的导光遵从所谓的包层模失配原理:当包层玻璃管直径为纤芯直径的1.3—1.4倍时,纤芯LP01模的有效折射率曲线正好位于包层玻璃管LP01和LP11模的有效折射率曲线的中间,可以实现单模传输(图9(a))[45].在玻璃管直径20.8µm、壁厚420 nm、管间距约3.7µm、纤芯直径14.6µm的条件下(图9(b)),实现了260—296 nm,322—422 nm,478—708 nm窗口的反谐振导光(图9(c)),最小损耗约0.3 dB/m,出现在355 nm波长.虽然这根尝试性光纤中还没有观察到双折射现象,但是我们实现了四阶旋转对称性的结构特征.

5 反谐振空芯光纤中弯曲损耗的机理研究和实验验证

除了限制损耗外,反谐振空芯光纤还存在较严重的弯曲损耗.事实上,弯曲损耗和限制损耗之间有一个相互折衷的关系.为了降低限制损耗,目前的反谐振光纤的芯径一般为波长的30—50倍,这使得在10 cm左右的弯曲半径下光纤损耗开始急剧增加,严重影响了反谐振空芯光纤的应用.为此,我们对弯曲损耗的产生机理和实验展示做了深入研究[30].

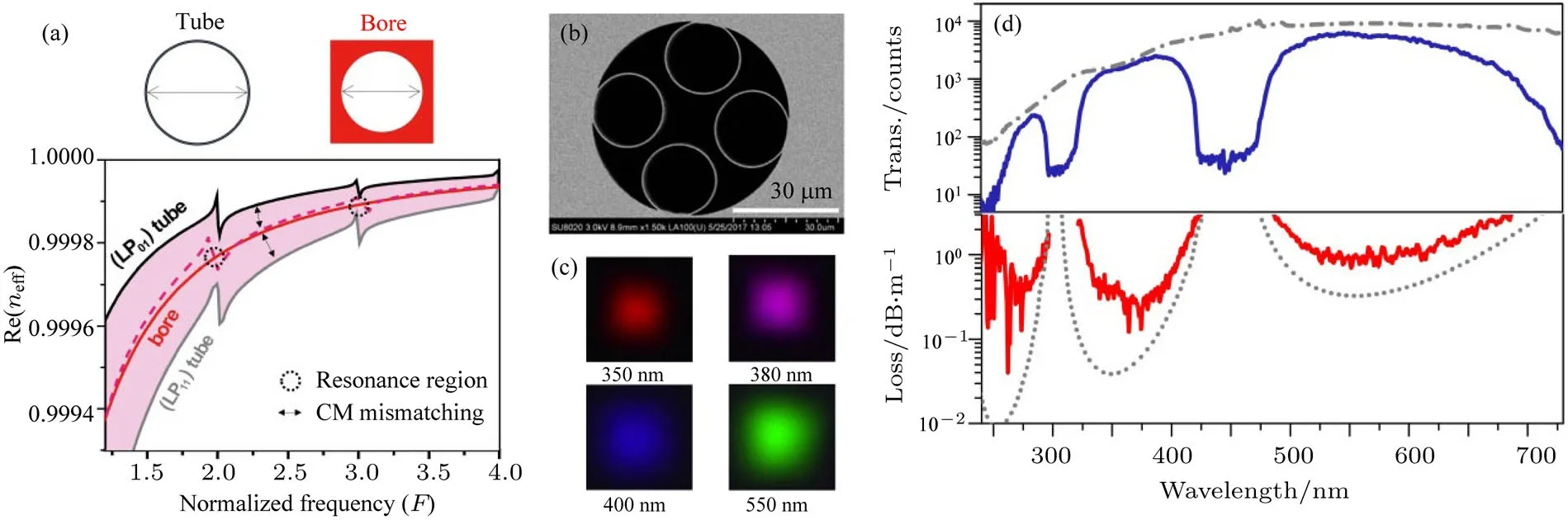
图9 (a)解析计算得到的直径20.8µm的玻璃管中的LP01模(黑色实线)和LP11模(灰色实线)以及毛细管直径16µm时的芯层模,玻璃管壁厚度为420 nm,红色虚线代表仿真计算得到的纤芯直径14.6µm时的负曲率光纤(4-tube)的模式色散曲线,归一化频率F=2t(n2−1)1/2/λ=2,3,···附近是反谐振通光窗口的边界;(b)负曲率光纤的扫描电子显微镜照片;(c)在350,380,400和550 nm带通滤波片之后拍摄的光纤输出端照片;(d)光纤传输和损耗谱,实线为测量结果,灰色点划线为氙灯光源光谱,灰色点线为仿真结果[28]Fig.9.(a)Analytically calculated dispersion curves of the LP01(black solid)and LP11(gray solid)airy modes of a cladding tube with the diameter of 20.8µm and the fundamental core mode with the bore diameter of 16µm(red solid).The thickness of the glass tube is 420 nm.The black double arrows indicate the “cladding mode mismatching” requirement.The red dashed line shows the simulated dispersion curve of the four-tube hollow-core negative curvature fi ber with the inscribed core diameter of 14.6µm.At the normalized frequency F=2t(n2 − 1)1/2/λ =2,3,···the anti-resonant re fl ecting optical waveguide band edges appear.(b)Scanning electron microscope image of the 4-tube hollow-core negative curvature fi ber.(c)Near fi eld mode pro fi les captured on a camera after bandpass fi lters centered at 350,380,400 and 550 nm,respectively.(d)Transmission and loss spectra of the fi ber.The solid lines are the measured results and the dotted gray line is the simulated result.The dash-dotted gray line is the spectrum of the xenon lamp source[28].

5.1 弯曲状态下短波长通光窗口的出现和理论解释

负曲率型反谐振空芯光纤的包层是由一圈互不接触的玻璃管环绕而成的(图10(a)).除了像第3节中那样将包层结构沿径向方向逐层切割之外,还可以把每个玻璃管当做一个独立个体来处理[45].

当光纤处于弯曲状态时,为了计算光纤中的模式,可以等效地将光纤横截面上的折射率乘上一个保角系数exp(x/Rb)[46],其中Rb为光纤弯曲半径,方向沿着−x轴.引入一个假设来降低计算复杂度:把每个玻璃管看作一个独立的个体,它对应的保角系数在一阶近似下等于一个常数exp(xc/Rb),xc为玻璃管中心位置的x坐标.在知道了光纤的尺寸和玻璃管的方位角之后,可以用柱坐标系中的传输矩阵方法精确地算出圆形玻璃管中的玻璃导模(模式系数的虚部为零)和空气泄漏模(模式系数的虚部不为零)的色散曲线.图10(b)和(c)中的虚线和细实线代表了这两类模.这两幅图分别计算了方位角位置不同的两对玻璃管的情况.把玻璃管的模式色散曲线和整根光纤的空气芯模式的色散曲线(图10(b)和(c)中的粗实线)进行比对,发现了一个有趣的现象:两者只在个别波长相匹配,在这些匹配波长之间的区域反谐振条件仍然满足(即光纤的包层结构对纤芯中光束的向外泄漏起到了阻碍的作用).将能够实现反谐振的连续的频率带宽(∆F)提取出来,表示为光纤弯曲半径Rb和玻璃管直径d的函数,图10(d)发现弯曲状态下的光纤仍能实现相当宽的导光.因此,基于负曲率空芯光纤中玻璃管数量的有限性,我们找到了一定程度上克服光纤弯曲损耗的方法.新的通光窗口出现在整个反谐振通带的短波一侧,最佳的弯曲导光状态出现在玻璃管直径较大、光纤弯曲半径适中(略小于10 cm)的情况下.

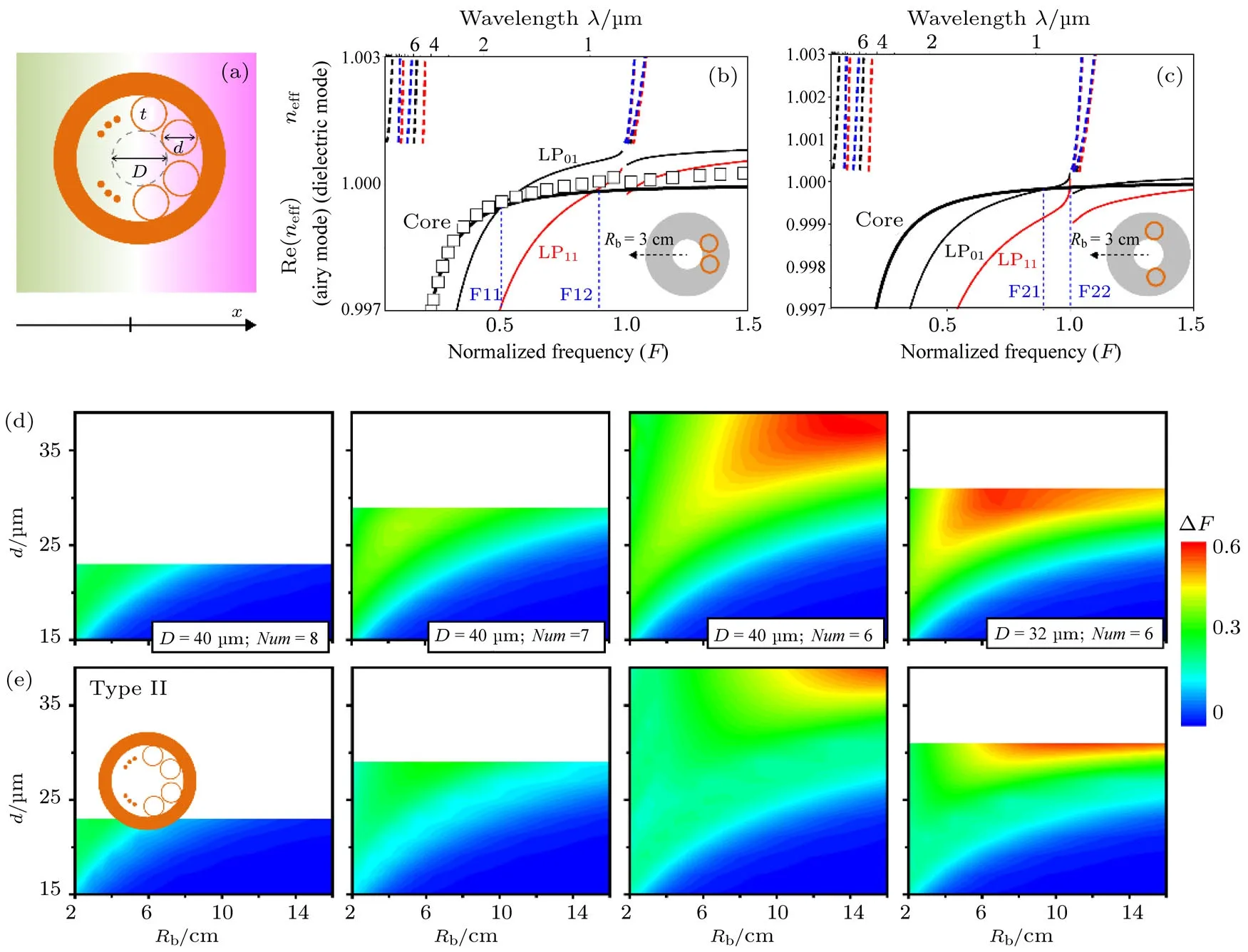
图10 (a)I类摆放姿态下的负曲率空芯光纤以及弯曲造成的折射率变化(保角因子)分布图;(b),(c)乘上保角因子后玻璃管结构的导模和泄漏模的模式系数色散曲线;(b)和(c)分别代表最外侧的和次外侧的两个玻璃管;D=40µm,d=24µm,t=410 nm,Num=7;对弯曲光纤纤芯模的色散曲线的简化计算(黑色粗实线)与精确的仿真计算(空芯方框)符合得很好;(d),(e)在反谐振窗口(F∈[0,1])的短波侧获得的连续通光区域的宽度(∆F)随弯曲半径和玻璃管直径变化的函数,(d)和(e)分别代表I类和II类摆放姿态下的弯曲情况[30]Fig.10.(a)Schematic illustration of the hollow-core negative curvature fi ber at the bending con fi guration of Type I and the e ff ect of the conformal mapping on the refractive index.(b),(c)Dispersion curves of the equivalent air core capillary(thick black line)and the tubes(dashed lines for dielectric modes and thin solid lines for airy modes)in the simpli fi ed model.The tubes in the outermost side(b)and in the second outermost position(c)under bending are respectively calculated with D=40µm,d=24µm,t=410 nm,and Num=7.Numerical simulation of the core mode of the actual fi ber(holy squares)agrees reasonably with the simpli fi ed modeling.(d),(e)The maximum frequency spans(∆F)acquired in the short wavelength side as a function of the bending radius and the tube diameter for the(d)Type I and(e)Type II fi ber bending con fi gurations[30].

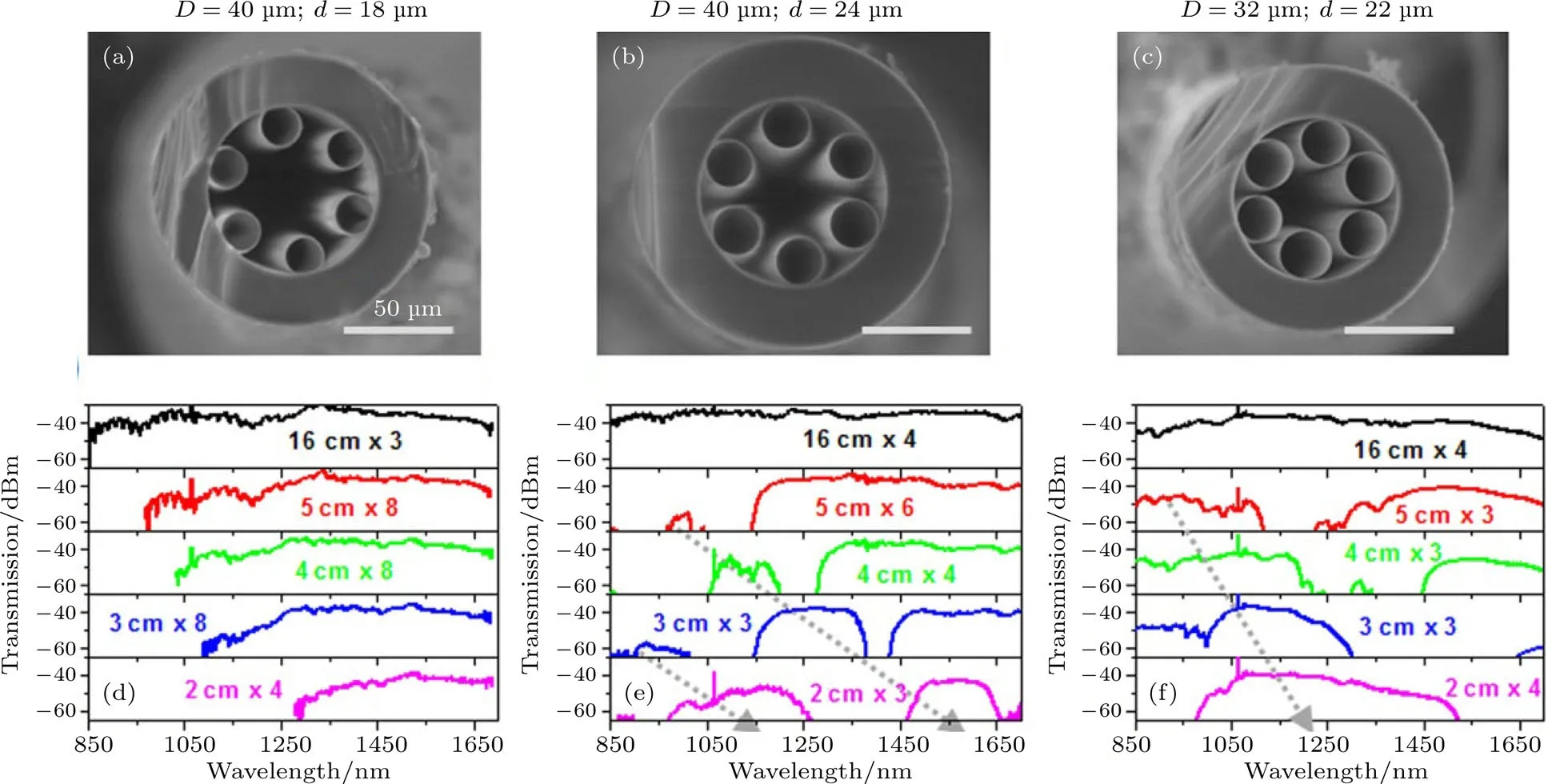
图11 (a)—(c)#1,#2,#3负曲率空芯光纤的扫描电子显微镜照片;(d)—(f)三根光纤在不同弯曲半径下的透射谱;图标表示了弯曲半径 × 盘绕圈数[30]Fig.11.(a)–(c)Scanning electron microscope images of hollow-core negative curvature fi ber#1,#2,#3 having di ff erent tube sizes and core radii as indicated,all the scanning electron microscope images have the same scale bar;(d)–(f)transmission spectra of the three fi bers under di ff erent bending radii,and the legend in each graph denotes bending radius in cm×number of turns[30].

如果考虑光纤的摆放姿态相对于光纤弯曲方向的夹角(图10(e)),上述结论仍然成立.在图10的计算中,限定了光纤中玻璃管的数量为6—8个,这被认为是能够实现低损耗、高模式纯度的最佳范围.显然,玻璃管数量为6时最有利于实现反谐振光纤的弯曲导光.

5.2 弯曲损耗的实验测量

我们在实验上检验了上述理论.图11(a)—(c)给出了三根光纤(#1—#3)的扫描电子显微镜照片,6个互不接触的玻璃管壁厚为410 nm.#1号光纤的纤芯直径为40µm,玻璃管直径18µm,玻璃管间距11µm.#2号和#3号光纤的参数分别为(40µm,24µm,8µm)和(32µm,22µm,5µm).#3号光纤是其中最符合弯曲状态导光的结构.当光纤直着摆放或者弯曲半径较大(Rb=16 cm)时,三根光纤的通光性能非常相似(图11(d)—(f)中的黑色曲线),测量得到的传输损耗在100 dB/km的水平.当弯曲半径减小为5—2 cm时,光纤的通光窗口逐渐向长波方向移动(图11(d)—(f)中的红色、绿色、蓝色、粉色曲线).最显著的特征出现在#2号和#3号光纤弯曲半径Rb<5 cm时,新的非常宽带的通光窗口在短波侧逐渐形成.例如,在图11(f)的粉色曲线中短波的通光窗口的宽度达到了110 THz的量级(从980 nm到1520 nm).这代表了一个在弯曲状态下反谐振光纤导光的有效方法,也验证了5.1节对导光机理的近似计算的正确性.

6 总结与展望

过去十年间,受益于更早十年开启的研究工作的积累和新结构的发现,反谐振空芯光纤研究迅速发展成为空芯光纤领域的最前沿.这类空芯光纤不仅在传输损耗和单模纯净度方面达到了光子带隙空芯光纤的水平,还拥有后者无法企及的宽带导光和超高激光损伤阈值的好处.它必将成为各种光与物质相互作用应用的优良载体,在超短超强激光脉冲传输[47]、单周期脉冲产生[48,49]、低延迟光通信[50]、紫外光源[51]、中红外气体激光[31,52]、生物化学传感[39,53]、量子光学[54,55]和近红外到太赫兹波段波导[56]等大量的交叉学科研究中发挥重大作用.

从几何对称性的角度来看,我们发现反谐振空芯光纤可以理解为光子带隙空芯光纤和布拉格空芯光纤的混合体.首先,它以熔石英为唯一基础材料,不仅使光纤的制作技术更成熟(更有利于形状的精确控制)、材料纯度更高(更有利于降低吸收和瑞利散射损耗),而且可以发挥包层区域由单一类型玻璃界面组成的好处(对光束的向外泄漏具有更加强烈的阻拦效果).其次,反谐振空芯光纤中的光场相干相消作用主要发生在与玻璃壁垂直的方向上(与布拉格光纤类似),而光能的向外辐射则并不局限在径向方向上(与光子带隙空芯光纤类似).正是由于这种混合型的结构特征,反谐振空芯光纤的导光机理的复杂度适中,它的光束囚禁作用的灵活度也适中.这使得我们意识到有可能建立一套半解析的理论模型来直观地分析反谐振空芯光纤的损耗问题,并对其结构进行优化设计.

我们的做法是把局域性的光场相干相消作用和全局性的辐射能流叠加作用分开来处理.突出体现在第2节中将光纤玻璃壁分块处理之后再进行积分叠加的过程中.这一方法的成功应用清晰地阐明了反谐振导光机制和光子禁带导光/布拉格导光之间的区别,后两者都是基于全局性布拉格反射效应的导光机制.在上述理论的基础上,我们发明了一套具有较高精度的半解析计算光纤限制损耗的模型.

在第3节中,我们把实际的光纤包层结构引入分析,提出了将负曲率光纤进行逐层分割的想法;阐明了影响导光的四项物理机制,给出了描述限制损耗的总方程.在不考虑Fano谐振影响的前提下,这个总方程可以推广应用到更广泛的反谐振空芯光纤结构中去.我们在实验上也实现了从紫外到中红外各个波段的光纤制作.

在第4节中,应用上述理论阐明了混合型反谐振通光窗口的机理以及光纤中双折射-偏振损耗之间的K-K关系和10−4量级的宽带双折射效应;完成了实验制作双折射反谐振空芯光纤的第一步(一根具有四重旋转对称性的光纤).在第5节中,运用类似的理论又研究了光纤的弯曲损耗,解决了如何在弯曲状态下进行反谐振空芯光纤导光的问题,并得到了实验验证.

本文回顾了我们对反谐振空芯光纤导光机理和实验加工的研究进展;用直观的物理图像解释了许多发生在这类光纤中的光学现象,提出了完整的可以定量化计算的模型.我们的理论可以用来对光纤性质进行非常直接的优化设计,避免了求解逆向问题时会遇到的麻烦.我们的实验工作突破了光纤拉制过程中的多个技术困难,完美检验了理论,也为接下来在这类光纤上进行更多创新性的应用打下了坚实的基础.展望未来五年,我们相信反谐振空芯光纤一定会在进一步降低传输损耗和拓展光纤应用方面取得更大的突破.

[1]Kao K C,Hockham A 1966 Proc.IEEE 113 1151

[2]Russel P St J 2003 Science 299 358

[3]Born M,Wolf E 1999 Principles of Optics:Electromagnetic Theory of Propagation,Interference and Di ff raction of Light(6th Ed.)(Cambridge:Cambridge University Press)pp47–50

[4]Maier S A 2007 Plasmonics:Fundamentals and Applications(New York:Springer)pp11–15

[5]Yablonovitch E 1987 Phys.Rev.Lett.58 2059

[6]Joannopoulos J D,Johnson S G,Winn J N,Meade R D 2008 Photonic Crystals:Molding the Flow of Light(2nd Ed.)(Princeton:Princeton University)pp156–189

[7]Birks T A,Roberts P J,Russell P St J,Atkin D M,Shepherd T J 1995 Electron.Lett.31 1941

[8]Fink Y,Winn J N,Fan S,Chen C,Michel J,Joannopoulos J D,Thomas E L 1998 Science 282 1679

[9]Knight J C 2003 Nature 424 847

[10]Johnson S G,Ibanescu M,Skorobogatiy M,Weisberg O,Engeness T D,Soljačić M,Jacobs S A,Joannopoulos J D,Fink Y 2001 Opt.Express 9 748

[11]Roberts P,Couny F,Sabert H,Mangan B,Williams D,Farr L,Mason M,Tomlinson A,Birks T,Knight J C,Russell P St J 2005 Opt.Express 13 236

[12]Duguay M A,Kokubun Y,Koch T L,Pfei ff er L 1986 Appl.Phys.Lett.49 13

[13]Litchinitser N M,Abeeluck A K,Headley C,Eggleton B J 2002 Opt.Lett.27 1592

[14]Benabid F,Roberts P J 2011 J.Mod.Opt.58 87

[15]PolettiF,PetrovichM N,RichardsonD J2013 Nanophotonics 2 315

[16]Birks T A,Bird D M,Hedley T D,Pottage J M,Russell P St J 2004 Opt.Express 12 69

[17]Pottage J M,Bird D M,Hedley T D,Birks T A,Knight J C,Russell P St J,Roberts P J 2003 Opt.Express 11 2854

[18]Ferrarini D,Vincetti L,Zoboli M,Cucinotta A,Selleri S 2002 Opt.Express 10 1314

[19]White T P,Kuhlmey B T,McPhedran R C,Maystre D,Renversez G,de Sterke C M,Botten L C 2002 J.Opt.Soc.Am.B 19 2322

[20]Aghaie K Z,Fan S H,Digonnet M J F 2010 IEEE J.Quantum Elect.46 920

[21]Yeh P,Yariv A,Marom E 1978 J.Opt.Soc.Am.68 1196

[22]Marcatili E,Schmeltzer R 1964 Bell Syst.Tech.J.43 1783

[23]Temelkuran B,Hart S D,Benoit G,Joannopoulos J,Fink Y 2002 Nature 420 650

[24]Mangan B,Farr L,Langford A,Roberts P J,Williams D P,Couny F,Lawman M,Mason M,Coupland S,Flea R,Sabert H,Birks T A,Knight J C,Russell P St J 2004 Optical Fiber Communication Conference Los Angeles,February 23–27,PD24

[25]Ding W,Wang Y Y 2014 Opt.Express 22 27242

[26]Ding W,Wang Y Y 2015 Front.Phys.3 16

[27]Wang Y Y,Ding W 2017 Opt.Express 25 33122

[28]Gao S F,Wang Y Y,Ding W,Wang P 2018 Opt.Lett.43 1347

[29]Gao S F,Wang Y Y,Liu X L,Hong C,Gu S,Wang P 2017 Opt.Lett.42 61

[30]Gao S F,Wang Y Y,Liu X L,Ding W,Wang P 2016 Opt.Express 24 14801

[31]Cao L,Gao S F,Peng Z G,Wang X C,Wang Y Y,Wang P 2018 Opt.Express 26 5609

[32]Ding W,Wang Y Y 2015 Opt.Express 23 21165

[33]Cregan R F,Mangan B J,Knight J C,Birks T A,Russell P St J,Roberts P J,Allan D C 1999 Science 285 1537

[34]Marcuse D 1991 Theory of Dielectric Optical Waveguides(2nd Ed.)(London:Academic Press)pp7–19

[35]Michieletto M,Lyngs J K,Jakobsen C,Lgsgaard J,Bang O,Alkeskjold T T 2016 Opt.Express 24 7103

[36]Uebel P,Günendi M C,Frosz M H,Ahmed G,Edavalath N N,Ménard J-M,Russell P St J 2016 Opt.Lett.41 1961[37]Hayes J R,Sandoghchi S R,Bradley T D,Liu Z,Slavik R,Gouveia M A,Wheeler N V,Jasion G,Chen Y,Fokoua E N,Petrovich M N,Richardson D J,Poletti F 2017 J.Lightwave Technol.35 437

[38]Chafer M,Delahaye F,Amrani F,Debord B,Gérôme F,Benabid F 2018 Conference on Lasers and Electro-Optics San Jose,May 13–18,paper SF1K.3

[39]Liu X L,Ding W,Wang Y Y,Gao S F,Cao L,Feng X,Wang P 2017 Opt.Lett.42 863

[40]Vincetti L,Setti V 2012 Opt.Express 20 14350

[41]Gao S F,Wang Y Y,Liu X L,Gu S,Peng Z G,Wang P,Du K M 2017 Chin.J.Lasers 44 0201012

[42]Roberts P J,Williams D P,Sabert H,Mangan B J,Bird D M,Birks T A,Knight J C,Russell P St J 2006 Opt.Express 14 7329

[43]Fini J M,Nicholson J W,Mangan B,Meng L,Windeler R S,Monberg E M,DeSantolo A,DiMarcello F V,Mukasa K 2014 Nat.Commun.5 5085

[44]Haakestad M W,Skaar J 2005 Opt.Express 13 9922

[45]Vincetti L,Setti V 2010 Opt.Express 18 23133

[46]Olszewski J,Szpulak M,Urbańczyk W 2005 Opt.Express 13 6015

[47]Debord B,Alharbi M,Vincetti L,Husakou A,Fourcade-Dutin C,Hoenninger C,Mottay E,Gérôme F,Benabid F 2014 Opt.Express 22 10735

[48]Elu U,Baudisch M,Pires H,Tani F,Frosz M H,Köttig F,Ermolov A,Russell P St J,Biegert J 2017 Optica 4 1024

[49]Balciunas T,Fourcade-Dutin C,Fan G,Witting T,Voronin A A,Zheltikov A M,Gerome F,Paulus G G,Baltuska A,Benabid F 2015 Nat.Commun.6 6117

[50]Poletti F,Wheeler N V,Petrovich M N,Baddela N,Fokoua E N,Hayes J R,Gray D R,Li Z,Slavík R,Richardson D J 2013 Nat.Photon.7 279

[51]Köttig F,Tani F,Biersach C M,Travers J C,Russell P St J 2017 Optica 4 1272

[52]Hassan M R A,Yu F,Wadsworth W J,Knight J C 2016 Optica 3 218

[53]Cubillas A M,Unterko fl er S,Euser T G,Etzold B J M,Jones A C,Sadler P J,Wasserscheid P,Russell P St J 2013 Chem.Soc.Rev.42 8629

[54]Okaba S,Takano T,Benabid F,Bradley T,Vincetti L,Maizelis Z,Yampol’skii V,Nori F,Katori H 2014 Nat.Commun.5 4096

[55]Sprague M R,Michelberger P S,Champion T F M,England D G,Nunn J,Jin X M,Kolthammer W S,Abdolvand A,Russell P St J,Walmsley I A 2014 Nat.Photon.8 287

[56]Yang J,Zhao J,Gong C,Tian H,Sun L,Chen P,Lin L,Liu W 2016 Opt.Express 24 22454