激光在大气中驱动的强太赫兹辐射的理论和实验研究∗

2018-07-10 09:32王伟民张亮亮李玉同盛政明张杰3

物理学报 2018年12期

关键词：偏振赫兹等离子体

王伟民张亮亮李玉同盛政明张杰3)

1)(中国科学院物理研究所,北京凝聚态物理国家研究中心,北京 100190)

2)(首都师范大学物理系,北京 100048)

3)(中国科学院大学物理科学学院,北京 100049)

4)(上海交通大学物理与天文学院,上海 200240)

(2018年3月29日收到;2018年5月2日收到修改稿)

1 引言

如何获得参数可调的强太赫兹辐射源是目前太赫兹研究中最重要的问题之一.一方面,高功率太赫兹波可以用于太赫兹通信、快速太赫兹成像等领域[1].另一方面,强太赫兹辐射可以用来开展目前几乎还是空白的强太赫兹辐射与物质非线性相互作用的基础研究,譬如强太赫兹抽运半导体、金属、超导体等关联电子材料引起的光电新特性,短脉冲强太赫兹引起的半导体、超导体相变和非平衡态诱发等,太赫兹非线性光学,材料的强磁场效应等.

过去二十多年的研究表明:强激光驱动的等离子体可以产生参数可调的强太赫兹辐射源[2−12].譬如中国科学院物理研究所强场物理课题组[5,13,14]和德国耶拿大学[6]分别采用脉宽约100 fs、聚焦强度高于1018W/cm2的相对论强激光作用固体靶,在靶前和靶后均观察到毫焦量级、超宽频谱的强太赫兹波.靶前产生的太赫兹波在低激光对比度条件下可归结为线性模式转换机制[4],在高对比度条件下可归结为表面电流机制[5].靶后产生的太赫兹波大致可以归结为渡越辐射机制[14].用强度为1014—1015W/cm2激光脉冲作用气体可以产生线偏振[3,15−19]、椭圆偏振[20−23]、径向偏振[10]的太赫兹辐射.这些基于强激光与等离子体相互作用的方案中,Cook和Hochstrasser在2000年提出的双色激光方案[3]因为技术简单和转化效率高的原因得到最广泛的研究,在此方案中通常用一束常规的800 nm飞秒激光(基频波)穿过一块倍频晶体产生400 nm激光(倍频波),后者与剩余的800 nm激光混合,在大气中就能产生MV/cm量级、线偏振、准单周期的强太赫兹波[3,15−19].

在2017年以前的实验中,双色方案实验中采用的两束激光频率比始终固定在ω2/ω1=1:2.尽管在最近的两个实验中为了把太赫兹波强度提高到接近10 MV/cm[24,25]而采用了波长更长的基频激光,但是两束激光频率比依然固定在1:2.2013年,我们最早从理论上研究了采用其他非常规激光频率比产生太赫兹波的可能性[26],发现:两束激光的频率比ω2/ω1=1:2n(n为正整数)就可以产生太赫兹波,当ω2/ω1=1:(2n+1)时不能产生太赫兹波.接着,Kostin等[27]在2016年、本课题组[28]在2017年根据不同的理论模型均发现了两束激光的频率比ω2/ω1还可以推广到其他更多的频率比.我们的粒子模拟和理论分析结果表明,Kostin等采用的理论模型及得到的结论是不正确的,并进一步把能够产生太赫兹波的频率比推广到ω2/ω1=2n,n+1/2,n±1/3三个系列,其中2n和n+1/2系列最稳定,也能最高效地产生太赫兹波[28].

这些理论预测在2017年首次被中国科学院物理研究所和首都师范大学联合团队的实验证实[29].在实验中把ω1激光的波长分别固定在800 nm和400 nm时,对ω2激光波长从1200 nm到1600 nm进行细致的扫描,观察到太赫兹能量的峰值点分别出现在ω2/ω1=1:4,1:2和2:3三个值附近,并且这三个峰值处的太赫兹波能量处于相同的量级.除了证实了之前的理论预测以外[26−28],实验中还观察到通过旋转ω2激光的偏振可以对太赫兹波的偏振进行调控,但是旋转ω1激光时这种偏振调控方法失效(注意:在本文中我们把ω1激光定义为较高频的激光,ω2激光为较低频的激光).这些观察结果与粒子模拟结果相符.

由于这些实验[29]采用了不同于1:2的非常规的激光频率比,它为澄清太赫兹辐射机制提供了新的突破口.自从2000年提出双色激光方案以来的十多年里,太赫兹辐射的物理机制应该归结为最初提出的非线性光学的多波混频机制[3,15,30],还是后来提出的等离子体电流机制[16,17],或者两种机制均起作用,一直是一个被频繁讨论的问题,但至今仍没有定论.首先,多波混频理论预测当采用不同的激光频率比时,太赫兹能量应该遵守不同的定标率,如在原始方案中太赫兹能量εTHz正比于(P1)(P2)2(这里P1和P2表示两束激光的峰值功率);当两束激光的频率比为1:4和2:3时,εTHz正比于(P1)(P2)4和(P1)2(P2)3.但是,在实验中观察到εTHz对P1和P2的依赖关系很复杂,并且当采用不同的激光频率比时太赫兹能量的定标率并没有表现出明显的区别.其次,实验观察到太赫兹偏振仅能通过旋转较低频率的激光的偏振来实现,这与多波混频(大气中)理论中要求的极化率张量的对称性不相符[15].

本文接下来的内容包括:首先简单介绍我们在2013年和2017年的两个理论工作[26,28],通过粒子模拟和解析分析讨论了双色激光方案推广到其他非常规激光频率比的可能性及其条件;然后,详细地介绍我们在2017年的实验和理论分析[29],证实了以上理论预测.

2 理论预测:对双色激光方案的推广

2013年,我们利用一个基于等离子体电流理论的解析模型,分析第二束激光为第一束激光(主激光)频率的任意整数谐波时产生太赫兹辐射的特性[26].根据此模型得到第二束激光频率的选择定则:当第二束激光频率为主激光的任意奇数谐波时,无太赫兹波产生,这是由于激光对气体的电离具有严格的对称性,因而电离产生的总电流为0;当第二束激光频率为主激光的任意偶次谐波时,可以产生太赫兹波,这是由于两束激光对气体的电离的对称性被打破,因而电离产生的总电流比较强.当第二束激光频率为主激光的任意偶次谐波时,得到太赫兹场强对两束激光相位差θ0和截波包络相位的依赖关系为

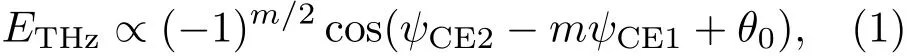
其中m为第二束激光频率对应的谐波阶数.以上结果与粒子模拟结果符合得很好,如图1所示:当第二束激光频率取为主激光频率的2,4,6倍频时均有太赫兹波产生;产生的太赫兹波强度随着激光频率增加而减小;太赫兹波强度随激光相位差呈余弦关系,并且2和6倍频情形满足−cos(θ)关系,4倍频情形满足cos(θ)关系,这与方程(1)一致.

图1 产生的太赫兹波强度随两束激光相位差的变化曲线(KLAPS粒子模拟结果) (a)和(b)对应的主激光强度分别为1014和1015W/cm2[26]Fig.1.Amplitudes of THz electric fi elds versus the relative phases of the second lasers with di ff erent frequencies.The circular,square and triangular points show particle-incell simulation results and the solid lines are cosine curves.Intensities of the main lasers are taken as 1014W/cm2in(a)and 1015W/cm2in(b),respectively.The second laser intensities are taken to be 25%of the main laser[26].

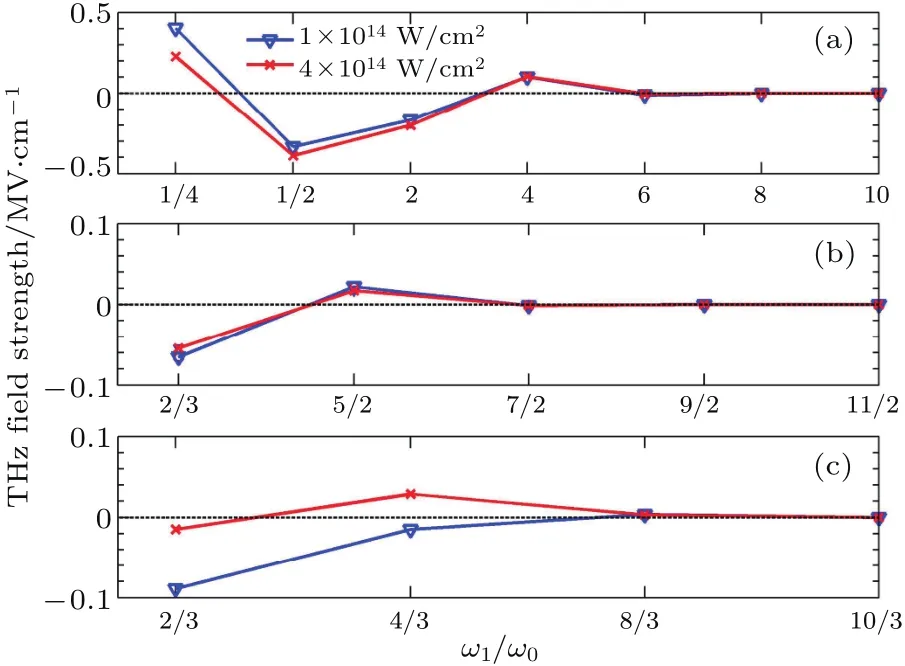
图2 产生的太赫兹波强度随两束激光频率比值的变化曲线(KLAPS粒子模拟结果),其中(a),(b),(c)分别对应着两束激光频率比为1:2n,1:(n+1/2),1:(n±1/3)的三个系列,每幅图中的两条曲线分别对应着不同的激光强度[28]Fig.2. The THz fi eld strength as a function of the two-color laser frequency ratio,where plots(a),(b),(c)correspond to di ff erent series of 1:2n,1:(n+1/2),and 1:(n±1/3)as well as the two curves in each plot correspond to laser intensities of 1014W/cm2and 4×1014W/cm2,respectively[28].

理论分析和粒子模拟结果均表明:第二束激光频率越低,产生的太赫兹波越强,因此它为二倍频光时,对太赫兹波的产生最有利.这是由于激光频率越高,在一个基频激光周期内的电离点数目会越多,不同电离点上产生的电子会具有方向相反的速度,因而产生的电流相互抵消,不利于太赫兹辐射的产生;反之,激光频率越低,在一个基频激光周期内的电离点数目会越少,一个基频激光周期内所有的电离点上产生的电子可能会具有方向相同的速度,因而产生的电流相互加强,从而产生的太赫兹辐射增强.进一步地,粒子模拟结果表明[28]:除了1:2n以外的频率组合,双色激光方案还可以推广到1:(n+1/2),1:(n±1/3),这两个系列的频率组合也能稳定和有效地产生太赫兹辐射.对应的粒子模拟结果见图2.

3 实验

3.1 实验装置

图3(a)为实验装置图.Ti:Sapphire激光装置(Spit fi re,Spectra Physics)输出中心波长为800 nm、脉冲宽度为50 fs、重复频率为1 kHz的抽运激光脉冲.抽运脉冲的总能量为5.3 mJ,它被分成两束,第一束激光脉冲能量为3.5 mJ用于驱动光学参数放大器(TOPAS),从光学参数放大器中输出的激光脉冲波长可以在1200 nm到1600 nm间调节(ω2激光);剩余的激光脉冲被直接作为波长为800 nm的ω1激光(如图3(c)).在另一组实验中(见图3(d)),800 nm激光脉冲穿过一块BBO(偏硼酸钡)晶体和滤波器以产生波长为400 nm的激光脉冲(ω1激光).用一块双色镜让ω1和ω2激光脉冲同轴传输,再用两块焦距长度(f=12.5 cm)相同的透镜对两束激光进行聚焦.一开始,两束线偏振激光的偏振方向均在水平方向上,它们的偏振能通过半波片分别调节.利用衰减片,两束激光的功率也能分别进行调节.两束激光在大气中能产生长度为毫米量级的等离子体通道.

用一个离轴抛物镜来收集和准直从气体等离子体中产生的前向传输的太赫兹波,并且滤波器(TydexLtd.)把两束多余的抽运激光消除掉.为了测量太赫兹波的水平和垂直分量,用到了太赫兹偏振片.一个Golay太赫兹探测器(6mm金刚石窗口,Microtech SN:220712-D)用来探测太赫兹能量,其中此探测器对0.1—150 THz波段的电磁波的响应曲线几乎是平的.电压信号送到锁相放大器参考15 Hz调制频率.为了获得太赫兹辐射的带宽,利用硅晶片作为分光片,用迈克耳孙干涉仪进行自相关测量.

图3 实验布局图和实验结果[29] (a)实验布局图,L表示透镜;DM表示双色镜;PM表示抛物镜;(b)—(d)实验结果,其中(c)和(d)中“×”点为实验结果,实线为KLAPS粒子模拟(PIC)结果;(b)当两束激光频率比ω2/ω1=1:4和2:3时,自相关测量获得的太赫兹时间波形,其中太赫兹波功率是以800 nm激光和1600 nm激光产生的太赫兹波功率为单位;(c)中第一束激光波长为800 nm,第二束激光波长在1200 nm到1600 nm间变化,发现太赫兹波能量峰值出现在1200 nm和1600 nm 附近(波长比为3:2和2:1);(d)中第一束激光波长为400 nm,当第二束激光波长为1600 nm时,出现太赫兹波能量峰值,对应的波长比为4:1,在两幅图中“×”点为实验结果,实线为KLAPS粒子模拟(PIC)结果Fig.3. Experimental results and setup[29]:(a)Experimental setup(L,lens;DM,dichromatic mirror;PM,parabolic mirrors);(b)THz waveforms with ω2/ω1=1:4 and 2:3,respectively,obtained from the autocorrelation measurements,in which the THz powers are normalized by the one with the 800 nm and 1600 nm pulses;(c),(d)THz energy as a function of the second pulse wavelength λ2,where the fi rst pulse wavelength λ1is fi xed as 800 nm in(c)and 400 nm in(d);powers of the two pulses are taken as P1=120 mW and P2=400 mW in(c)and P1=180 mW and P2=250 mW in(d).

3.2 实验与模拟结果

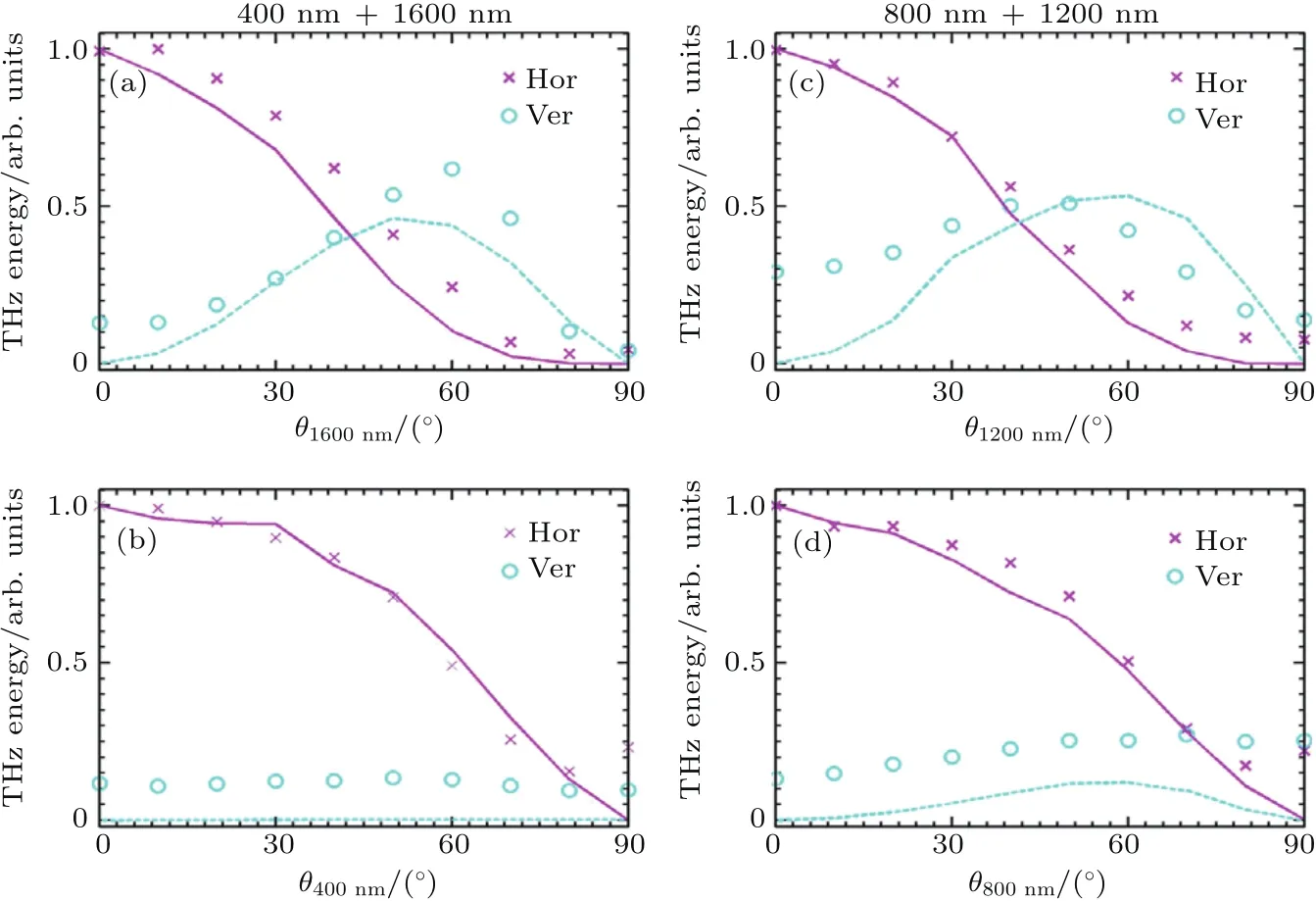
图4 对太赫兹波偏振的调节——太赫兹波水平和垂直分量能量随一束激光偏振旋转角θ的变化[29](a),(b)采用400 nm和1600 nm激光组合;(c),(d)采用800 nm和1200 nm激光组合;两束激光初始偏振均在水平方向上,然后分别旋转1600 nm激光的偏振(a),400 nm激光的偏振(b),旋转1200 nm激光的偏振(c),800 nm激光的偏振(d)让其具有垂直方向的分量;图中“o”点为实验结果,实线为KLAPS粒子模拟(PIC)结果Fig.4.Dependency of THz polarization[29]:THz energies of the horizontal and vertical components as a function of the rotation angle θ of the fi eld polarization of(a)the 1600 nm pulse,(b)400 nm pulse,(c)1200 nm pulse,and(d)800 nm pulse,respectively,where when polarization of one pulse is rotated,polarization of the other pulse is fi xed at the horizontal.Experimental results are shown by crosses and circles and particle-in-cell results by lines.The left column corresponds to the case with the 400 nm(with 180 mW)and 1600 nm(250 mW)pulses and the right to the case with the 800 nm(120 mW)and 1200 nm(400 mW)pulses.

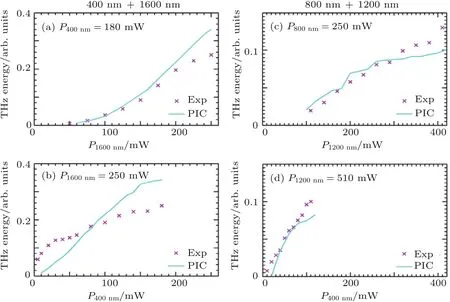
图5 太赫兹波能量随激光峰值功率的变化[29] (a),(b)采用400 nm和1600 nm激光组合;(c),(d)采用800 nm和1200 nm激光组合;图中“×”点为实验结果,实线为KLAPS粒子模拟(PIC)结果;当激光功率比较低时(曲线的开始阶段),在不同波长比情形均满足线性定标率Fig.5.Dependency of THz polarization[29]:THz energies of the horizontal and vertical components as a function of the rotation angle θ of the fi eld polarization of(a)the 1600 nm pulse,(b)400 nm pulse,(c)1200 nm pulse,and(d)800 nm pulse,respectively,where when polarization of one pulse is rotated,polarization of the other pulse is fi xed at the horizontal.Experimental results are shown by crosses and circles and particle-in-cell results by lines.The left column corresponds to the case with the 400 nm(with 180 mW)and 1600 nm(250 mW)pulses and the right to the case with the 800 nm(120 mW)and 1200 nm(400 mW)pulses.

我们首先给出实验和粒子模拟(PIC)结果,然后用一个基于等离子体电流模型的理论分析进行解释.在实验中观察到的太赫兹产生对ω2/ω1、激光偏振、激光功率的依赖关系如图3(b)—图5所示,在这些图中也包括粒子模拟结果(除图3(b)以外).首先,图3(b)给出了实验中探测到的太赫兹时间波形,可以看到当采用ω2/ω1=1:4和2:3时产生的太赫兹波与采用ω2/ω1=1:2时产生的太赫兹波比较,其峰值功率分别为后者的30%和10%左右.在图3(c)中对ω2激光的波长在1200—1600 nm间进行扫描,可以看到太赫兹波仅在ω2/ω1=2:3和1:2附近有效产生,其中ω1激光的波长固定在800 nm.在图3(d)中ω1激光的波长固定在400 nm,太赫兹波仅在 ω2/ω1=1:4附近有效产生.注意到实验中观察的太赫兹能量峰出现的位置与粒子模拟中预测的ω2/ω1=1:4,2:3,1:2时的结果有一个小的偏差,在实验中ω2激光的波长值偏离粒子模拟获得的波长值10—20 nm.这主要是由从TOPAS中输出的激光波长有小的偏差造成的.其次,图4显示太赫兹波的偏振能够通过旋转ω2激光 (较长波长)的偏振来调节,但是旋转ω1激光的偏振几乎不改变太赫兹偏振.当ω2/ω1=1:4(图4(a)和图4(b)),ω2/ω1=2:3(图4(c)和图4(d)),ω2/ω1=1:2时均能观察到类似的结果.例如,在图4(a)中当ω2/ω1=1:4时,波长为1600 nm的ω2激光的偏振从水平方向旋转到垂直方向时,太赫兹波的水平分量持续减弱,其垂直分量先增强再减弱,这一现象与其他作者采用ω2/ω1=1:2时得到的实验结果类似.但是,波长为400 nm的ω2激光偏振旋转时,太赫兹波的垂直分量始终保持着一个较低的水平,如图4(b)所示,其中太赫兹波的垂直分量的水平与旋转角θ=0◦和90◦时相当,因此认为其处于噪声水平.以上实验结果与粒子模拟结果符合得很好.再次,太赫兹能量对激光功率的依赖与多波混频理论预测的能量定标率不符,如图5所示.图5中ω2/ω1=1:4和2:3对应的两条曲线显示出复杂的依赖关系.特别地,所有曲线在开始阶段均显示出太赫兹能量对激光功率线性的依赖关系,这与粒子模拟结果大致吻合.

4 理论分析

粒子模拟结果(辐射的近场分布)和实验结果(辐射的远场分布)的一致性表明在实验中观察到的太赫兹远场分布应该主要来自于激光脉冲经过自聚焦达到最高场强时在大气中形成的一小段等离子体辐射,其中粒子模拟计算了这段气体与激光的相互作用过程.在粒子模拟中采用了一段0.6 mm长的氮气,采用了与实验相同的激光参数,并假设激光传输到这段气体的前沿时激光脉冲刚好达到它的最高光强(1014—1015W/cm2量级),此时激光的焦斑半径为50µm.此粒子模拟结果用KLAPS程序计算得到[31],此程序包括计算气体场电离的蒙特卡罗方法,产生的自由电子的运动用相对论的运动方程进行计算,用完整的麦克斯韦方程组计算激光和太赫兹波的产生和传输.因此,KLAPS粒子模拟程序能自洽地计算等离子体的产生、净电流通过激光场电离的形成过程、净电流在等离子体中的演化以及太赫兹波的产生.该粒子模拟得到太赫兹波的近场解时几乎没有近似.一般可以认为实验上观察到的太赫兹波的远场结果是由所有近场太赫兹辐射源组成的[19].

为了解释粒子模拟结果和实验结果,做了一个基于等离子体电流模型的理论分析.2007年,Kim等[16]首先提出双色激光场气体电离过程中的不对称性导致了电流的形成.但是他们的模型无法解释实验中观察到的电磁波为什么是准单周期波形,及其频率为什么处于太赫兹波段.2008年,我们[17]指出激光电离形成的等离子体至关重要,并提出了一个等离子体电流模型(为近场模型):首先等离子体把净电流调制成振荡电流,其频率处于等离子体本征振荡频率ωp,因而该电流辐射的电磁波频率为ωp;因为频率为ωp的电磁波在等离子体中的折射率为0而被强烈吸收,因而只有距等离子体边界足够近的区域(接近1个趋肤长度ωp/c)产生的电磁辐射能最终进入真空/大气中,并且该辐射源随时间逐渐衰减,因此在大气中观察到的电磁波为准单周期波形.2011年,我们从该等离子体模型出发,推导出太赫兹辐射波形的解析解[32],并在2015年把此模型推广到磁化等离子体中[23],发现在外加磁场下太赫兹波变成圆偏振,其波形由单周期变成多周期,其频率可由磁场强度线性调节.

在等离子体电流理论中,太赫兹波的产生过程包括两个过程:首先净电流通过光场电离产生,然后净电流被等离子体调制产生了太赫兹辐射.第一个过程持续的时间少于激光脉冲宽度(脉冲宽度为50 fs),第二个过程的时间尺度为皮秒量级.因此可以认为第一个过程发生后,第二个过程才开始发生,这样可以把两个过程分开计算.电离形成的净电流[17]J0=−enev0能够写为

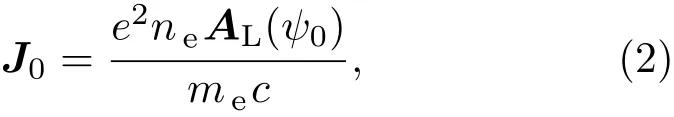
其中v0= −eAL(ψ0)/(mec),AL是激光场矢势;ψ=t−z/c,ψ0为电子通过电离过程产生的位置.注意到当采用不同的ω2/ω1=1:4,1:2,2:3时,两束激光仍然会组成周期性的电场(忽略激光包络的变化时),因此电子会被周期性地产生,并且电子会在每个周期中相同的位置产生,具体细节请见文献[28].形成的等离子体电子密度可以写为∂ne/∂t=(na− ne)w(EL),其中w(EL)为电离率[33],EL为激光电场强度,ne和na为电子密度和氮原子初始密度.当激光离开后,产生的太赫兹波与等离子体电流相互作用,因此电子速度变成v=v0+eATHz/(mec),即等离子体电流变成J=J0−e2neATHz/(mec),其中太赫兹波的优质动力(二阶非线性项)太弱,只考虑了太赫兹波对电子洛仑兹力的一阶项.这样,太赫兹波的产生可以由下面的方程进行描述:

其中是等离子体本征振荡频率.由于太赫兹波的脉冲宽度大于其横向尺寸(∼50µm),一维近似是不适用的[32],因此方程(3)的解析解很难给出.下面的理论分析将对方程(2)做数值解,对方程(3)做简单分析即可解释以上的实验结果.

4.1 太赫兹波对激光频率比的依赖

从方程(2)和(3)出发,能得到太赫兹波场强ATHz∝J0∝AL(ψ0).太赫兹波能量峰值会出现在AL(ψ0)处.我们的计算显示AL(ψ0)具有三个峰值点,分别位于ω2/ω1=1:4,1:2,2:3.为了定量地比较这三个峰值点上的太赫兹能量,通过方程(2)数值计算了AL(ψ0),neJ0和J0,得到的结果显示:当ω2/ω1=1:4,1:2,2:3时,得到J0的比值为0.29:1:(−0.58),即对应的太赫兹能量比值应该为0.084:1:0.34.这与实验中得到的0.097:1:0.26相符,如图3(c)和图3(d)所示.

4.2 太赫兹波偏振

根据方程(2)和(3),如果两束激光的偏振方向均沿着x方向,那么太赫兹波将只有x方向的电场分量.如果对一束激光的偏振进行旋转,让它的电场也具有y方向的分量,那么太赫兹波可能同时具有x和y两个方向的分量.取激光电场为

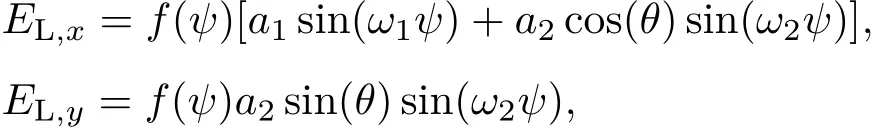
其中θ为激光的旋转角,f(ψ)为激光的包络形状.那么激光的矢势可以写成

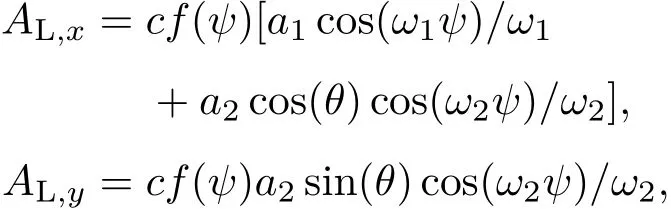
这里已经考虑了激光脉冲宽度为50 fs时ω1和ω2.电子在激光强度峰值

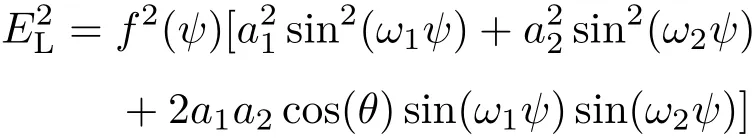
处产生,即满足当θ=0时,数值解以上方程可以得到ω2ψ0=1.937,其中通过激光功率P400nm=180 mW和P1600nm=250 mW分别计算得到a1和a2.数值计算显示ψ0略微随θ的改变而改变,这是因为当ω2ψ0=1.937时,这表明当cos(θ)从1变到0时(θ从0变到π/2),只需要对ψ0做一个小量ε变化即可让总是成立.

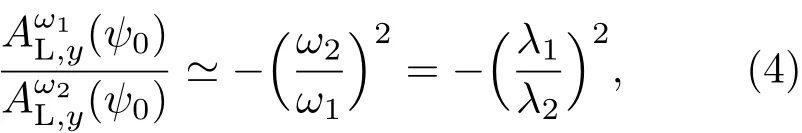
在图4(b)中旋转波长为400 nm激光(ω1激光)的偏振时,太赫兹波垂直分量始终保持着一个较低水平(在实验结果中它在噪声水平,在粒子模拟中它接近0). 其解释如下. 无论旋转ω1激光还是旋转ω2激光,|EL|是不变的,因此当θ=0时,给出了相同的结果ω2ψ0=1.937,ψ0略微随 θ变化.因此,在图4(b)中太赫兹波的水平分量随θ的变化规律与图4(a)类似.但是,太赫兹波的垂直分量强烈地依赖于激光频率或波长.当旋转ω1激光时,cf(ψ0)a1sin(θ)cos(ω1ψ0)/ω1. 当旋转ω2激光时,这样能够得到其中在推导过程中已经采用了a1ω1cos(ω1ψ0)=此结果从得到,这样利用了ψ0略微随θ变化. 通过方程(4),可以得到太赫兹波垂直分量的能量下降到1/256≃0.004,当把旋转的激光由ω2激光变成ω1激光时,这里ω2/ω1=1:4;当ω2/ω1=2:3时,太赫兹波垂直分量的能量下降到16/81≃0.2.这与图4(b)和图4(d)中的粒子模拟结果符合得很好.注意到实验中无法分辨低水平的太赫兹能量,实验中观察到太赫兹波垂直分量的能量几乎不随θ变化.当采用波长为800 nm和1600 nm的双色激光时,可以观察到相似的实验结果.

以上在实验中观察到的太赫兹偏振特性与多波混频理论的预测是不符的[15]. 例如,当ω2/ω1=1:4时大气中五阶极化率张量χ的对称性要求其中χ的上标表示太赫兹波的偏振方向,下标表示1个ω1激光光子和四个ω2激光光子的偏振方向.很显然,要求图4(a)中太赫兹波的水平分量能量与图4(b)中太赫兹波的垂直分量能量相当.相反地,图4(a)和图4(b)的结果表明

4.3 太赫兹波能量定标率

图5显示:当ω2/ω1=1:4和2:3时,太赫兹波能量对激光功率的定标率比较复杂,强烈地偏离多波混频理论预测的定标率(P1)(P2)4和(P1)2(P2)3(分别对应着ω2/ω1=1:4和2:3).这可以归结为电离率对激光强度的复杂依赖关系,实验中激光功率或强度变化跨越了两个数量级的区间,这为理论分析带来了难度.但是,当把一束激光的功率的变化限定在一个小的区间[Pa,Pb]内,并且第二束激光的功率固定在一个高得多的值Pc,即Pc≫Pb时,理论分析会简化很多.在这种情形下,随着第一束激光功率在[Pa,Pb]内变化,气体电离率几乎不随电离位置ψ0变化.以上描述的条件对应着图5中四幅图中每条曲线的开始阶段.当两束激光的偏振方向相同时容易得到∂ψ或者如上分析,当激光功率满足P1≫ P2和P1≪ P2时,ψ0几乎不随两束激光场强a1和a2的改变而变化.因此,|AL,x(ψ0)|线性地正比于a1或a2,即太赫兹能量线性正比于P1或P2.此线性定标率的预测与图5的实验结果和模拟结果是吻合的,即无论ω2/ω1=1:4还是2:3均能看到这曲线的开始阶段太赫兹能量线性定标于激光功率.注意到相似的实验结果已在文献[25]中观察到,其中ω2/ω1=1:2.在图5中能够看到粒子模拟与实验结果并不能精确地吻合,其可能原因如下:粒子模拟中假设了在最强自聚焦情形下不同功率激光的横向尺寸始终固定为50µm,这显然并不完全正确,最强自聚焦时不同功率激光对应的横向尺寸应该是依赖于激光功率的.但是,探索此复杂的依赖关系需要专门的研究.

5 结论

已有实验结果显示,当把激光频率比ω2/ω1由1:2变成1:4和2:3时,双色激光方案依然能有效地产生太赫兹辐射.相比于旋转两束激光中较短波长的激光,旋转较长波长激光的偏振能够更加有效地调节太赫兹波的偏振.这与多波混频理论的预测不相符,但是符合等离子体电流理论——根据该理论可推导出太赫兹波垂直分量能量与激光波长的四次方成正比.实验观察到太赫兹波能量对激光功率的依赖关系很复杂,并且当采用不同的激光频率比时太赫兹能量的定标率并没有表现出明显的区别;当一束激光功率远高于另外一束激光功率时,改变后者的功率观察到太赫兹能量对激光功率具有线性的依赖关系.这些结果与多波混频的预测不符,但是与粒子模拟结果和基于等离子体电流理论符合得很好.考虑到我们采用的激光强度为1014—1015W/cm2(一般双色场实验中采用的激光强度范围),以上结论对通常的实验是适用的,但是当激光强度低于1014W/cm2,等离子体电流很弱时的情况还需要进一步研究.总之,该工作首次从实验上演示了双色激光方案可以被推广到其他非寻常频率比ω2/ω1,并且通过实验和理论分析表明双色激光方案的物理机制应该主要归结为等离子体电流模型.

[1]Ulbricht R,Hendry E,Shan J,Heinz T F,Bonn M 2011 Rev.Mod.Phys.83 543

[2]Hamster H,Sullivan A,Gordon S,White W,Falcone R W 1993 Phys.Rev.Lett.71 2725

[3]Cook D J,Hochstrasser R M 2000 Opt.Lett.25 1210

[4]Sheng Z M,Mima K,Zhang J,Sanuki H 2005 Phys.Rev.Lett.94 095003

[5]Li Y T,Li C,Zhou M L,Wang W M,Du F,Ding W J,Lin X X,Liu F,Sheng Z M,Peng X Y,Chen L M,Ma J L,Lu X,Wang Z H,Wei Z Y,Zhang J 2012 Appl.Phys.Lett.100 254101

[6]Gopal A,Herzer S,Schmidt A,Singh P,Reinhard A,Ziegler W,Brommel D,Karmakar A,Gibbon P,Dillner U,May T,Meyer H G,Paulus G G 2013 Phys.Rev.Lett.111 074802

[7]Jin Z,Chen Z L,Zhuo H B,Kon A,Nakatsutsumi M,Wang H B,Zhang B H,Gu Y Q,Wu Y C,Zhu B,Wang L,Yu M Y,Sheng Z M,Kodama R 2011 Phys.Rev.Lett.107 265003

[8]Dey I,Jana K,Fedorov V Y,Koulouklidis A D,Mondal A,Shaikh M,Sarkar D,Lad A D,Tzortzakis S,Couairon A,Kumar G R 2017 Nat.Commun.8 1184

[9]Jin Q,E Y,Williams K,Dai J,Zhang X C 2017 Appl.Phys.Lett.111 071103

[10]D’Amico C,Houard A,Franco M,Prade B,Mysyrowicz A,Couairon A,Tikhonchuk V T 2007 Phys.Rev.Lett.98 235002

[11]Wang W M,Kawata S,Sheng Z M,Li Y T,Zhang J,Chen L M,Qian L J,Zhang J 2011 Opt.Lett.36 2608

[12]Bai Y,Song L,Xu R,Li C,Liu P,Zeng Z,Zhang Z,Lu H,Li R,Xu Z 2012 Phys.Rev.Lett.108 255004

[13]Liao G Q,Li Y T,Li C,Su L N,Zheng Y,Liu M,Wang W M,Hu Z D,Yan W C,Dunn J,Nilsen J,Hunter J,Liu Y,Wang X,Chen L M,Ma J L,Lu X,Jin Z,Kodama R,Sheng Z M,Zhang J 2015 Phys.Rev.Lett.114 255001

[14]Liao G Q,Li Y T,Zhang Y H,Liu H,Ge X L,Yang S,Wei W Q,Yuan X H,Deng Y Q,Zhu B J,Zhang Z,Wang W M,Sheng Z M,Chen L M,Lu X,Ma J L,Wang X,Zhang J 2016 Phys.Rev.Lett.116 205003

[15]Xie X,Dai J,Zhang X C 2006 Phys.Rev.Lett.96 075005

[16]Kim K Y,Glownia J H,Taylor A J,Rodriguez G 2007 Opt.Express 15 4577

[17]Wang W M,Sheng Z M,Wu H C,Chen M,Li C,Zhang J,Mima M 2008 Opt.Express 16 16999

[18]Wang W M,Gibbon P,Sheng Z M,Li Y T 2014 Phys.Rev.A 90 023808

[19]Zhang Z,Chen Y,Chen M,Zhang Z,Yu J,Sheng Z,Zhang J 2016 Phys.Rev.Lett.117 243901

[20]Wu H C,Meyer-ter-Vehn J,Sheng Z M 2008 New J.Phys.10 043001

[21]Dai J,Karpowicz N,Zhang X C 2009 Phys.Rev.Lett.103 023001

[22]Wen H,Lindenberg A M 2009 Phys.Rev.Lett.103 023902

[23]Wang W M,Gibbon P,Sheng Z M,Li Y T 2015 Phys.Rev.Lett.114 253901

[24]Clerici M,Peccianti M,Schmidt B E,Caspani L,Shalaby M,Giguere M,Lotti A,Couairon A,Legare F,Ozaki T,Faccio D,Morandotti R 2013 Phys.Rev.Lett.110 253901

[25]Vvedenskii N V,Korytin A I,Kostin V A,Murzanev A A,Silaev A A,Stepanov A N 2014 Phys.Rev.Lett.112 055004

[26]Wang W M,Li Y T,Sheng Z M,Lu X,Zhang J 2013 Phys.Rev.E 87 033108

[27]Kostin V A,Laryushin I D,Silaev A A,Vvedenskii N V 2016 Phys.Rev.Lett.117 035003

[28]Wang W M,Sheng Z M,Li Y T,Zhang Y,Zhang J 2017 Phys.Rev.A 96 023844

[29]Zhang L L,Wang W M,Wu T,Zhang R,Zhang S J,Zhang C L,Zhang Y,Sheng Z M,Zhang X C 2017 Phys.Rev.Lett.119 235001

[30]Liu K,Koulouklidis A D,Papazoglou D G,Tzortzakis S,Zhang X C 2016 Optica 3 605

[31]Wang W M,Gibbon P,Sheng Z M,Li Y T 2015 Phys.Rev.E 91 013101

[32]Wang W M,Kawata S,Sheng Z M,Li Y T,Zhang J 2011 Phys.Plasmas 18 073108

[33]Penetrante B M,Bardsley J N 1991 Phys.Rev.A 43 3100