新型高分辨率电子能量损失谱仪与表面元激发研究∗

朱学涛1)2) 郭建东1)2)†

1)(中国科学院物理研究所,表面物理国家重点实验室,北京 100190)

2)(北京凝聚态物理国家研究中心,北京 100190)

(2018年4月13日收到;2018年4月23日收到修改稿)

1 引 言

电子能量损失谱(electron energy loss spectroscopy,EELS)是随着超高真空技术的革新在过去四十多年间迅速兴起的一种分析技术.它以高度单色化的电子为入射粒子,激发固体材料电子的带间/带内跃迁以及其他多种元激发,通过测量非弹性散射电子的能量分布研究这些准粒子的特征.当入射电子的能量在千电子伏量级或更高时,通常可以将样品芯态能级上的电子激发到真空能级,这样的高能EELS利用鉴别每种元素的特征损失峰来确定化学成分.高能EELS谱仪大多装备在透射电子显微镜系统上[1],依赖于电子束聚焦与实空间成像能力,可以给出高空间分辨率的元素分布图.近年来发展出的高能电子分析器进一步将其能量分辨率提高到优于10 meV水平,能够开展具有空间分辨的晶格动力学观测[2].当入射电子的能量在200 eV以下时,表面散射引起的能量损失通常对应着材料表面晶格或表面吸附分子的振动,或外层电子态的跃迁以及电荷集体振荡等的激发,因此低能EELS可以测量电子的带边结构、声子和表面等离激元等.因低能EELS具备很高的能量分辨率(约1 meV量级),通常被称作高分辨率电子能量损失谱(HREELS)[3].特别是对晶格声子的探测,与拉曼散射相比,由于HREELS的激发源——电子具有比光子大得多的动量,具有很强的动量分辨本领.另外HREELS高质量的数据还可以给出准粒子寿命(线宽)的信息,因此在研究以电子-声子耦合[4]为代表的凝聚态物理问题方面具有不可替代的优势.此外,利用具有动量分辨能力的HREELS可以研究激子凝聚[5]等凝聚态体系中最基本的物理问题.

传统的HREELS谱仪所用的分析器不能在多个角度同时测量散射电子的能量,所以其角分辨的测量必须通过转动样品、电子源或分析器来实现.因此,探测器的狭缝宽度成为决定能量和动量分辨率的重要因素,而在动量空间的采样密度及重复性由机械转动的精度决定,所以测量效率较低.特别是对于声子色散的测量,如果用一个较高的采样密度来覆盖布里渊区中的某个方向,传统HREELS一般需要数十个小时来完成.由于HREELS是一个表面敏感的探测手段,即便是在超高真空中,样品表面也会在经过长时间后受到污染,从而使得来自样品本征的信息受到干扰.对于需要原位解理或原位生长的材料,短时间内完成高效率的测量尤为重要.因此,如果能够将传统HREELS谱仪对能量一维解析而对动量逐点测量的传统方式改为同时对能量/动量的二维探测,将明显提高测量效率.最近,我们研制出了具有高角分辨能力的电子束源,与商业化的半球形电子能量分析仪相结合,实现了对能量/动量的二维探测.这种新型的具有二维探测能力的高分辨电子能量损失谱仪(2D-HREELS)[6]能够消除测量中由于机械转动所引起的误差,在保证高能量/动量分辨率的前提下,大幅提高了动量分辨测量的效率(测量时间缩短约一个数量级),使整个动量分辨测量时间仅取决于探测器信号的积累时间,最大限度地避免了测量中清洁表面或吸附界面随测量时间的退化;同时大幅提高了能量/动量空间的采样密度(二维相平面上的采样密度提高约三个数量级).该2D-HREELS谱仪可以对表面元激发进行高分辨、高效率的测量,能够给出电子、晶格及其集体激发的综合信息,为研究低维材料体系中准粒子的相互作用提供了强大的工具.

元激发和准粒子是凝聚态物理的核心概念,特别是体系中的低能元激发及其相互作用对材料物理性质的形成起关键作用.对准粒子的精密测量是理解强关联物理、新奇物性起源的基础.能量、动量谱能够给出准粒子动力学的全面信息,因此新型2D-HREELS谱仪在动量分辨率、动量分辨测量效率以及测量范围方面的优势具有重要应用.本文以界面超导和拓扑绝缘体两个体系为例,详细讨论2D-HREELS谱仪在表面元激发的测量与研究中所取得的进展.

2 新型电子能量损失谱仪的研制

2.1 基本思路

HREELS通过探测低能电子与样品表面相互作用之后出射电子与入射电子之间的能量差及散射角,根据能量守恒原则获得样品表面准粒子的能量,根据动量守恒原则获得其动量.当一束能量为Ei、动量为ki的电子束以入射角θi与样品表面相互作用,在散射角θs处其散射动量为ks、能量为Es,如图1(a)所示,散射电子相对入射电子的能量损失(即准粒子的能量)为

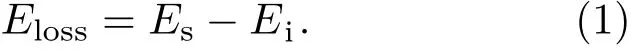
根据平行于表面面内的动量守恒,可以得到

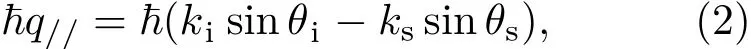
其中,~为普朗克常数,q//为探测到的准粒子在平行于表面的动量. 结合电子的动能关系(m为电子的质量),可以得到准粒子动量与散射角度和能量的表达式:

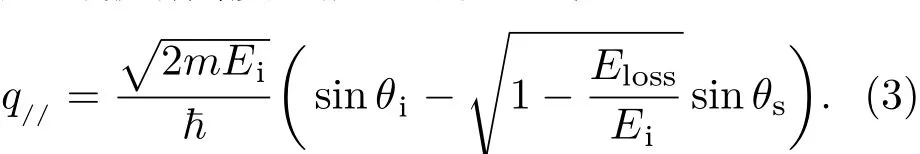
特别地,对于声子的测量,总是满足Eloss≪ Ei,(3)式可以简化为

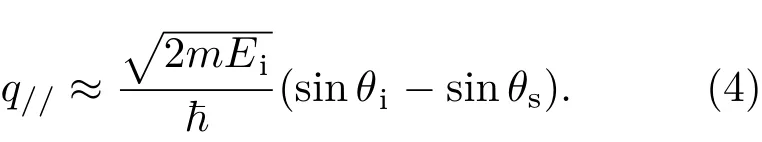
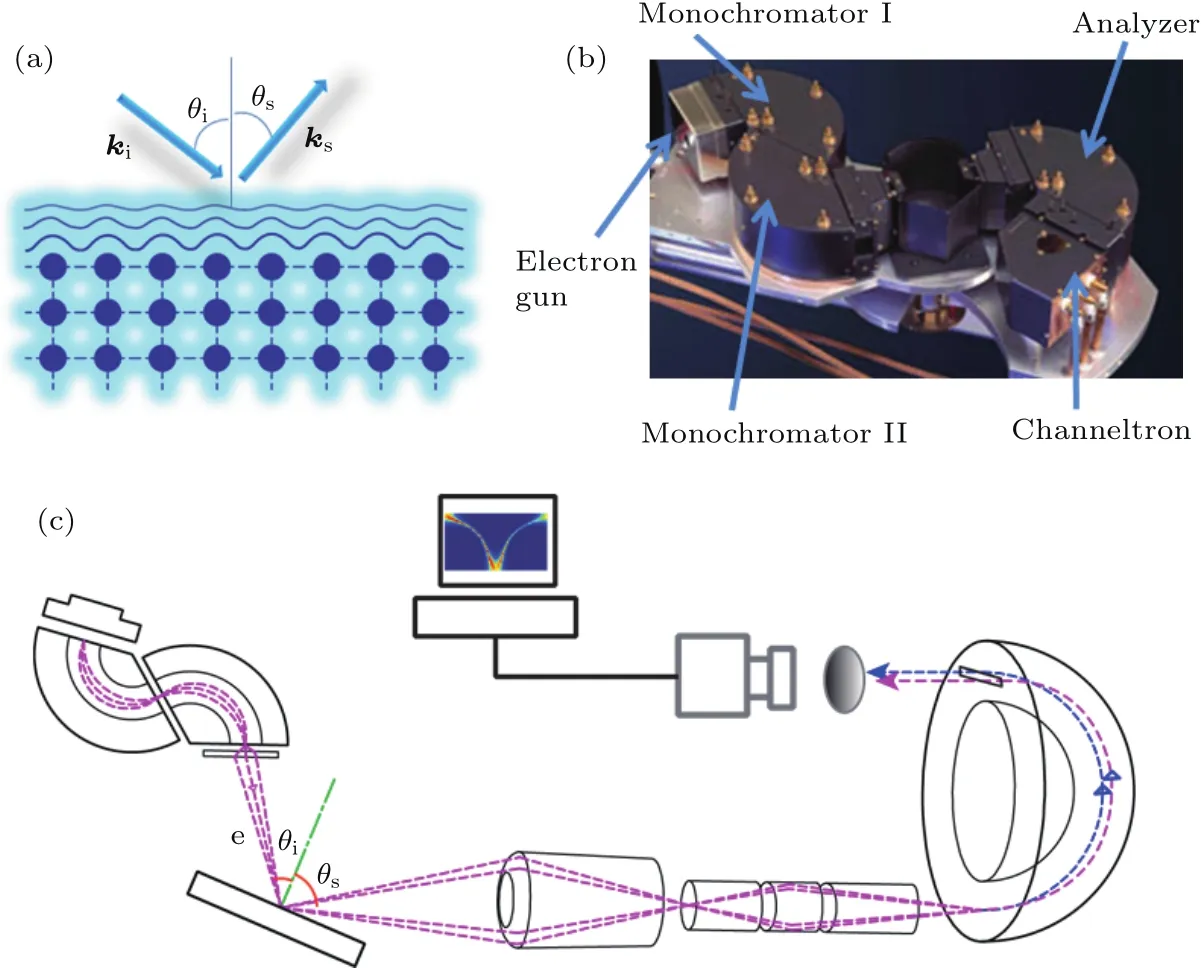
图1 (a)HREELS电子束散射示意图;(b)传统商业化HREELS谱仪结构实物照片,型号ELS-5000,美国LK Technologies公司,http://www.lktech.com/;(c)新型2D-HREELS谱仪结构和电子路径示意图Fig.1.(a)Schematic drawing of the electron scattering geometry in HREELS;(b)the setup of traditional commercial HREELS,ELS-5000 from LK Technologies(http://www.lktech.com/);(c)the schematic of the structure and the trace of the electron beam in the 2D-HREELS system.

传统的HREELS为了测量得到表面准粒子的色散(即Eloss与q//的对应关系),需要改变电子束的入射能量Ei、入射角θi及散射角θs等参数,以获得不同的动量值及动量范围.以目前世界上设计应用最广泛的HREELS谱仪,即美国LK Technologies公司制作的ELS5000型HREELS为例(德国SPECS公司也有同类产品,其设计与性能完全一样)[7,8],这种谱仪的电子激发源经过两个127◦的扇形单色器使其能量单一化,而散射电子经收集狭缝进入单个127◦扇形能量分析器实现能量解析(见图1(b)),这种设计可以达到很高的能量分辨率,约为1 meV(直通电子束理论设计可达0.5 meV).但它的动量分辨测量通常要依靠机械转动分析器改变散射角θs来实现,因此其角分辨率仅可以达到大约1◦.对于一般的测量参数,入射角为60◦,入射电子能量50 eV,对能量损失为50 meV散射电子的动量分辨率为0.06 Å−1.而且ELS5000谱仪在动量空间的测量是逐点完成的,也就是需要固定散射角即水平动量传递,按散射电子能量逐一计数,再手动改变散射角,重复能量解析计数.如前所述,这种一维的逐点测量方式在动量空间测量的采样密度受到很大的限制,重复性也比较差,效率低,成为制约HREELS方法更广泛、更方便地应用于声子色散谱等问题研究的瓶颈.

为了突破这一瓶颈,我们设计了利用半球形电子能量分析器实现同时对能量/动量进行二维探测的HREELS谱仪.目前的半球型电子能量分析器可以在一个方向上利用电子飞行轨道半径的不同确定电子的能量,而在垂直的另一个方向上同时分辨电子的散射角度,在探测器上呈现出以能量/动量为X/Y轴的二维强度分布图,从而高精度地解析散射电子能量、动量及散射强度.目前商业化的半球型电子能量分析器主要应用在角分辨光电子能谱(angle-resolved photoemission spectroscopy,ARPES)中.回顾ARPES方法的发展历史可以发现,二维探测器的应用[9]大大拓展和深化了ARPES的研究能力,使其成为测量电子谱函数并进而研究以电子-声子耦合为代表的强关联物理问题的强大工具[10,11].由于ARPES和HREELS所需要测量的电子能量和动量范围都比较接近,所以在HREELS中同样可以使用二维探测器.目前商业化的半球型电子能量分析器适用的探测能量和动量范围涵盖了一般的EELS的能量动量区间,将其与传统HREELS的双扇形电子单色器联用,如图1(c)所示,就可以把传统谱仪对能量一维解析而对动量逐点测量的方式,革新为同时对能量/动量的二维探测,从而在保证高能量/动量分辨率的前提下,提高动量分辨测量的效率以及能量/动量空间的采样密度.

2.2 研制要点

传统的HREELS谱仪中,单色器的出射透镜和分析器的入射透镜呈对称设计,用以减小电子束的发散角.如果简单地将传统的HREELS电子激发源与半球形分析器组合起来,这种不对称的空间结构会极大地增加电子束的发散角,从而影响角分辨率.我们详细研究了在对HREELS散射电子信号进行能量、动量解析过程中的电子运动轨迹和规律及其与电子受到样品表面散射前后动能和运动方向的关系.结果表明:激发源电子束的发散角度极其灵敏地影响信号强度和谱仪的动量分辨率(见表1),而其在样品表面形成束斑的大小在一定范围内并不起关键作用;要使半球形分析器获得优于0.5◦的角分辨率,激发源产生的电子束的发散角必须小于0.4◦,电子束的发散角度越小,使用半球形分析器得到的角分辨率就越高.因此,为了更好地实现二维分析器的诸多优势,必须重新设计电子激发源的出射透镜组,使其产生的电子束具有尽可能小的发散角.

表1 电子束信号强度与动量分辨率随激发电子发散角度的变化(能量4 eV,狭缝宽度0.5 mm)Table 1.Changes of the intensity and angular resolution of the electron beam as a function of the divergence angle.

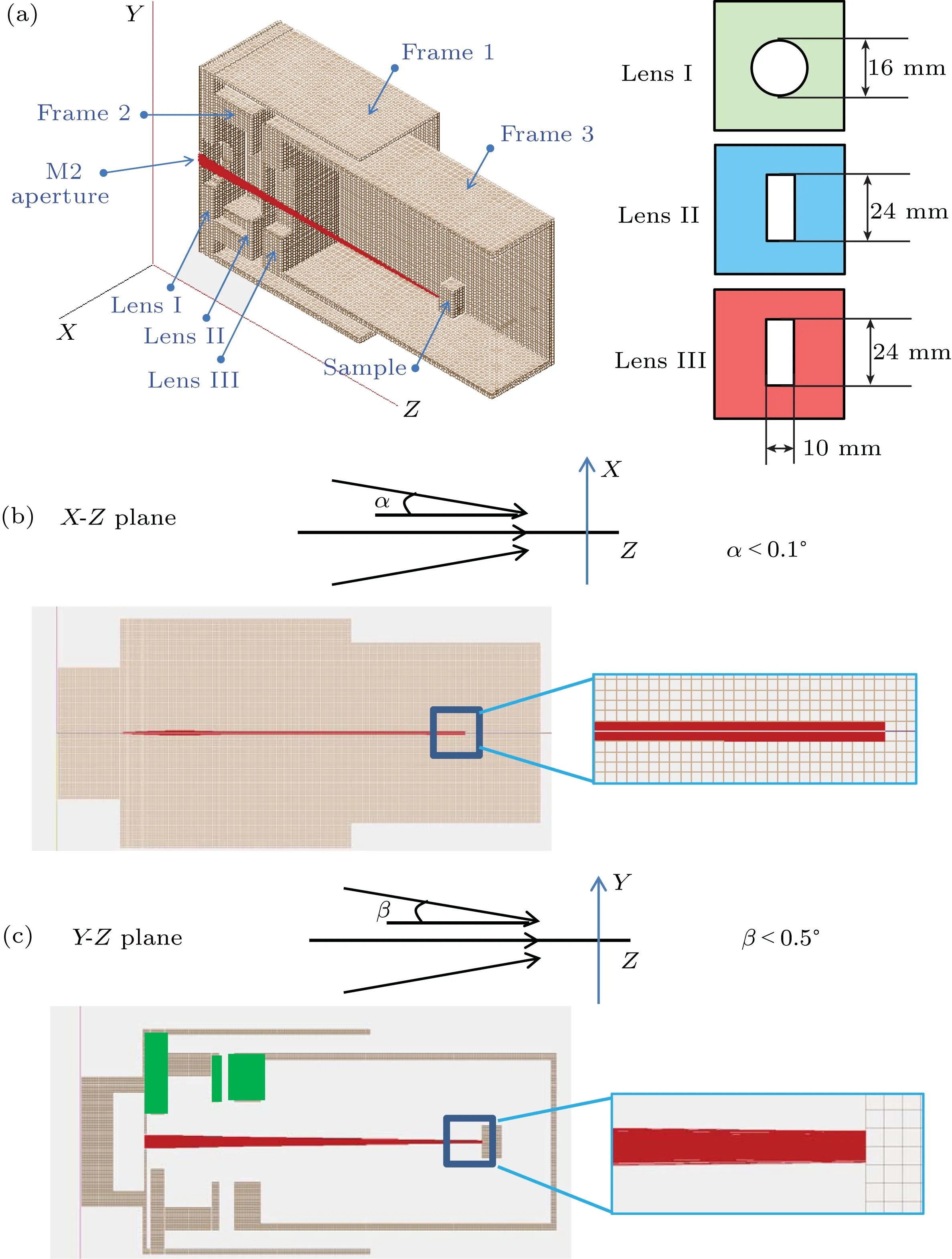
图2 高角分辨出射透镜组的设计和模拟图(经过AIP Publishing的授权,图片摘自文献[6]) (a)三个出射透镜的透视图和光圈尺寸示意图,红线表示模拟的电子束路径;(b)透镜组的顶视图,α为电子束在水平面内的发散角;(c)透镜组的前视图,β为电子束在竖直面内的发散角Fig.2.Design and simulation of the exit lens system with high-angular-resolution:(a)Perspective view of the three lens elements,and the red line indicates the simulated trace of the electron beam;(b)top view of panel(a)which shows the horizontal divergence angle α of the beam;(c)front view of panel(a)which shows the vertical divergence angle β of the beam.The fi gure was adapted from Ref.[6],copyright(2015)by AIP Publishing.

我们的设计主要是改进了美国LK Technologies公司的ELS5000型电子激发源的出射透镜组,在保证电子束能量分辨率的基础上,获得最小的电子束发散角.图2中详细展示了我们设计的特殊出射透镜组的结构和电子束发散角的模拟结果.这个出射透镜组由三个金属板透镜组成,每个金属板的中心开有一个不同形状的光圈[12],如图2(a)所示.在单色器的出射光圈M2处,ELS5000型电子激发源可以产生一个在X-Z平面中为0.3 mm,在Y-Z平面中为4 mm的长方形电子束,其在X-Z和Y-Z平面内的发散角分别为±3◦和±0.76◦.通过改变三个透镜的参数(位置及每个透镜的电压值),在每一组透镜参数组合下用软件模拟透镜组中电子束的发散角,最终确定最优的透镜参数,并得到优化后的最小发散角:X-Z和Y-Z平面内分别为±0.1◦和±0.5◦,如图2(b)和图2(c)所示.利用我们得到的参数制成透镜组,然后替换ELS5000型电子激发源上的出射透镜组,就可以得到具有高角分辨能力的电子激发源,从而与半球形电子分析器联用,实现2D-HREELS探测.研制好的高角分辨电子激发源在真空腔中安装在一个可以在水平面内旋转的平台上,其旋转与样品台的旋转同轴.通过调节电子激发源和样品的转动,可以调整电子束在样品表面的入射角θi.真空腔与电子源位置的安排见图3(a).

我们选用Scienta公司的R4000型高分辨半球形电子能量分析器作为探测器来测量散射电子的角度和能量.在选用最小的狭缝和最小的电子通能的情况下,该探测器的极限能量分辨率可达到0.25 meV,结合我们电子束源最好约0.5 meV的能量分辨率,最终谱仪的极限能量分辨率可以优于1 meV.电子的角分辨探测通过R4000分析器的三种角分辨模式来实现,接收角分别为7◦,14◦和30◦;7◦的模式可以用来进行高动量分辨的测量,而30◦的模式可以在一次测量中覆盖尽可能大的动量范围.此外,R4000分析器可以探测电子能量的范围为0.2—1000 eV,与我们采用的ELS5000型电子激发源产生的1—200 eV的电子束能量区间相适应.

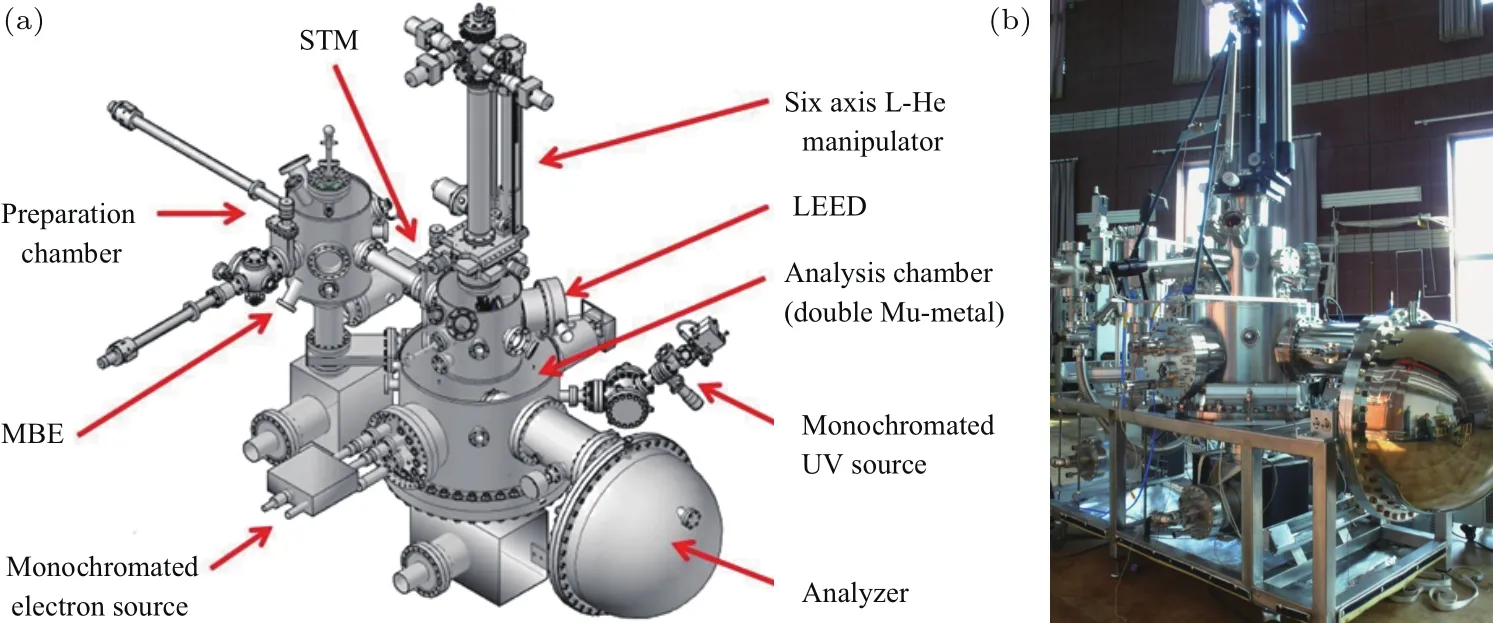
图3 (a)2D-HREELS谱仪真空系统三维设计图;(b)2D-HREELS谱仪实物照片Fig.3.(a)Illustration of the 2D-HREELS system design;(b)the onsite picture of the 2D-HREELS sytem.

谱仪的真空系统三维图和实物照片见图3.由于电子在磁场中会发生偏转,谱仪真空腔中的残余磁场要尽可能地小,因此我们选用具有优良磁场屏蔽能力的双层µ金属来制作谱仪的分析腔,使样品处的磁场强度小于2 mG(1 G=10−4T).分析腔的真空在烘烤之后可达到1.0×10−10Torr(1 Torr=1.33322×102Pa).分析腔的样品台采用包括三维平动以及三维转动的六轴样品台,并且安装有使用液氦连续流降温的低温系统,样品最低温度可以降至35 K.此外我们为谱仪配套设计了样品制备腔,配备了5轴样品台、离子溅射枪、金属蒸发源等,可以进行样品的原位解理、生长、表面处理、退火等,为HREELS谱仪的测量提供样品制备的保障.样品制备腔的真空度最低可达到6.5×10−11Torr.在制备腔中制备完成的样品会经过超高真空原位传样系统传入分析腔中的六维低温样品台上,在进行HREELS实验之前,可以使用分析腔中配备的低能电子衍射仪对样品的表面质量、晶格及晶向等信息进行表征.

特别地,我们在分析腔中配备了Scienta公司的VUV5000型紫外光源以及VUV5047型紫外光单色器,能够产生能量为21.2 eV(氦I)和40.8 eV(氦II)的单色化的紫外光.将紫外光与R4000型半球形电子能量分析器联用,可以进行ARPES测量.所以在分析腔中切换电子源和紫外光源,就可以方便地切换HREELS测量模式或ARPES测量模式,实现在同一套系统中对同样的样品进行原位电子结构与声子色散两个方面的测量,这对材料表面电子与声子相互作用的研究具有重要意义.

2.3 性能测试

谱仪安装之后,我们对谱仪的性能进行了详细的测量表征.通过测量电子直通束,即不经过样品散射,电子束直接由电子激发源打入半球形分析器,测得了谱仪的基本参数,主要包括:样品处的电子束斑大小为0.5 mm(半高全宽,FWHM);电子束的水平面内发散角约为0.3◦(与图2中的模拟结果相似);样品电流可以高达300 pA,与传统HREELS谱仪相似;谱仪的极限能量分辨率达到0.7 meV,与传统HREELS谱仪相似;极限动量分辨率高达0.002 Å−1,比传统HREELS谱仪提高约一个数量级.关于谱仪的设计、构成以及测试的详细信息,可以参见文献[6].

对于谱仪二维测量能力的展示,我们选用了典型的铜基高温超导体材料Bi2Sr2CaCuO8+δ(Bi2212)进行测量.Bi2212是一种易于原位解理的层状材料,并且有传统HREELS的测量数据[4]可资比较.在此项测试中,我们选用的HREELS参数包括:电子束入射能量Ei=60 eV,入射角θi=60◦,半球形探测器的通能Ep=5 eV.图4展示了测量结果.其中,图4(a)是散射强度在能量-动量二维平面上的分布图像;图4(b)是图4(a)沿能量方向对强度做二次微分后的结果;图4(c)是图4(a)在不同动量值处强度随能量的分布曲线,相当于传统HREELS谱仪测到的能量损失谱线的罗列.图4(a)明显地反映出了HREELS谱典型的散射特征:在镜面反射方向附近,即动量交换为0附近,在散射谱中占主导地位的是偶极子散射(dipole scattering);而在偏离镜面反射方向即动量交换较大的区域,在散射谱中占主导地位的是碰撞散射(impact scattering)[3].这两种散射机制具有不同的选择定则,因此能够反映测量到振动模式的对称性的信息.在偶极子散射的区域,3个能量损失峰非常明显,其在碰撞散射区域也有较强的信号(图中的1,3,5),其中能量在80 meV附近的模式具有明显的随动量增大而软化的特征,这与之前的传统HREELS谱仪的测量结果[4]基本一致.除了这3个模式,在图4(b)的二次微分谱中还能看到另外两个模式(图中的2,4),它们在偶极散射区域基本没有信号,只有在碰撞散射区内才能看到,很有可能对应着平行于表面的面内振动.这两个模式在类似于图4(c)的传统HREELS能谱测量中很难被分辨出来.

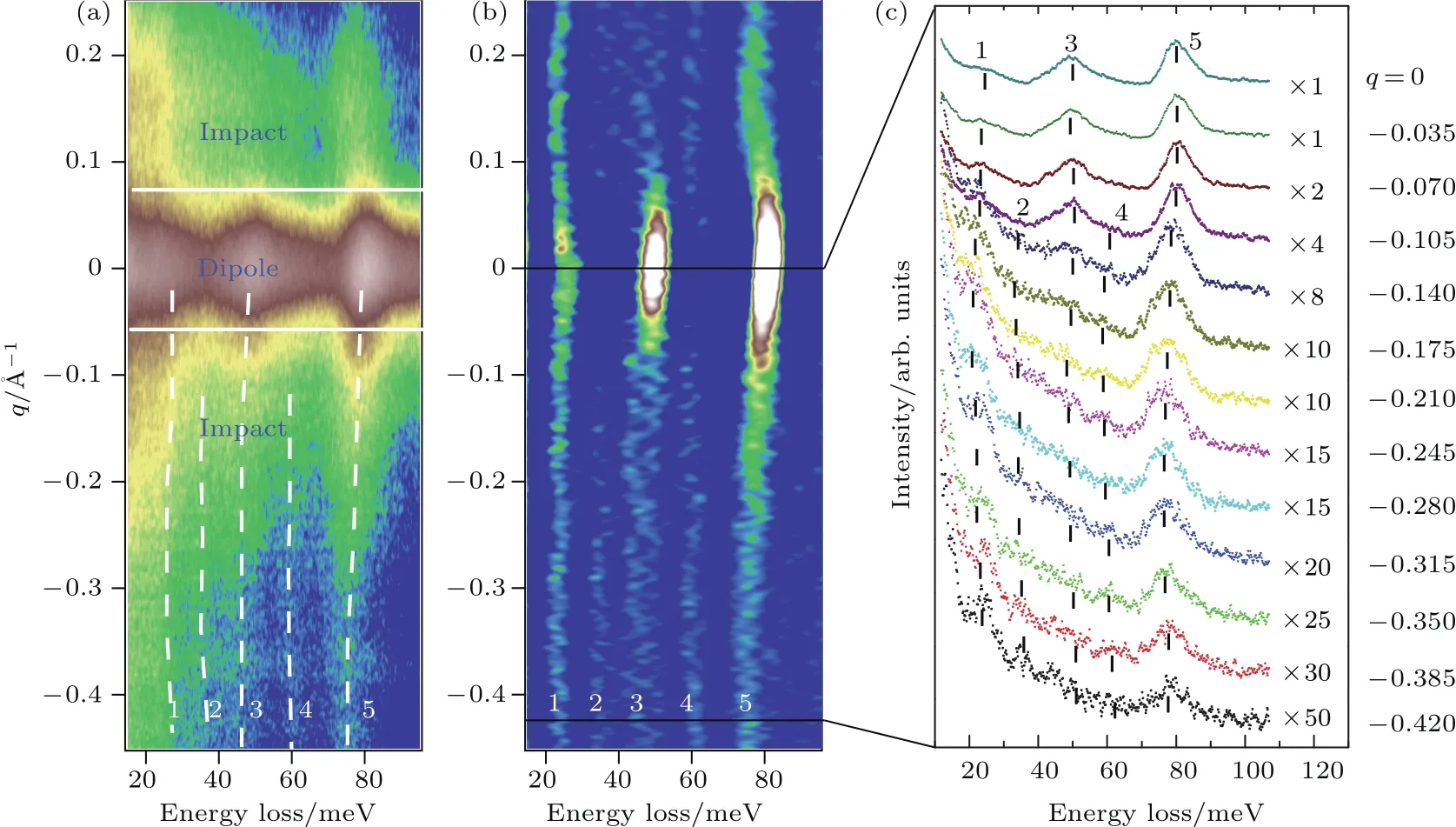
图4 (a)Bi2212样品沿着节线方向的HREELS散射强度在能量-动量二维轴上的分布图像,其中强度使用对数坐标绘制,测量参数为电子束入射能量Ei=60 eV,入射角θi=60◦,半球形探测器的通能Ep=5 eV,样品温度T=35 K,图中的虚线为测得的5个特征损失峰的示意曲线;(b)二维强度分布图沿能量方向做二次微分后的结果;(c)不同动量值处强度随损失能量的分布曲线,虚线为5个特征损失峰的示意曲线Fig.4.(a)2D-HREELS energy-momentum mapping of Bi2212 at T=35 K,with Ei=60 eV,θi=60◦,and Ep=5 eV,showing the inelastic scattering signal from Bi2212 along the nodal direction.The intensity is plotted in logarithmical scale.The dashed lines are guides to the eye of the 5 energy loss features.(b)The second derivative image along the energy deirection obtained from(a).(c)The energy distribution curves at di ff erent momentum values,with the dashed lines showing the 5 energy loss features.

新型2D-HREELS谱仪的最大优势之一就是其采样密度很大,不同于传统HREELS谱仪一次扫描测量得到一个动量-能量值,最终只能通过机械转动得到一组分立的动量-能量点,动量空间内的采样密度被机械转动的角度所限定.而新型2DHREES谱仪得到的是在动量空间内连续的能带.新型2D-HREELS谱仪的另外一大优势是其测量效率非常高.如图4(a)这样的二维谱是未经过任何样品或电子源的机械转动而一次扫描获得,采样时间由动量值最大处的信噪比决定.例如,图4(a)的采集大约为5 h.而传统的HREELS谱需要每个动量点都进行时间累积扫描,获得一个动量空间内比较合理的采样密度的谱需要至少数10 h.

3 FeSe/SrTiO3超导增强界面的晶格动力学研究

FeSe/SrTiO3界面的超导增强机制是近两年凝聚态物理研究的热点问题之一.薛其坤课题组于2012年初报道,单层FeSe/SrTiO3界面的超导能隙最高可达约20 meV,对应的超导转变温度(Tc)可能在液氮温区[13],远远高于体相FeSe材料的Tc(约8 K)[14].这种被界面大大增强的超导现象引起了科学家们的广泛关注.一方面,它为深入研究高温超导机理提供了相对简单又较为精确可控的体系;另一方面,它更易于通过外场实现对物理性质的人工调控,因此有望获得实际的器件应用.目前,单层FeSe/SrTiO3界面的超导研究已经成为凝聚态物理中,特别是界面超导领域研究的热点,产生了大量实验及理论方面的工作[15−18],目前普遍认为单层FeSe/SrTiO3体系的Tc可达到55—65 K.理解界面高温超导机制能够帮助寻找具有更高Tc的界面体系,并很有可能有助于理解普遍的高温超导机制.然而,FeSe/SrTiO3界面的超导增强机制目前尚不明确,是界面超导领域亟待解决的重大问题之一.

目前已有的大量研究结果表明,由衬底向FeSe薄膜的界面电荷转移是其界面超导增强不可或缺的因素[16−18].然而,在不存在衬底和界面的体相FeSe中,通过离子液体[19−21]、表面吸附碱金属[22,23]、元素插层[24,25]等多种方式掺入电子,在电子浓度达到单层FeSe/SrTiO3同样水平时,其Tc最多仅能达到40—45 K.单层FeSe/SrTiO3中肯定存在其他界面效应[26]来获得另外约20 K的Tc增强.特别是目前发现单层FeSe生长在SrTiO3的不同晶面上[27,28],或是在TiO2[29,30],BaTiO3[31]等其他含有Ti-O八面体的衬底上后,其超导Tc都能达到65 K左右.这一增强过程可以被称为FeSe超导Tc的“三级跳”,如图5所示,FeSe体相Tc约为8 K;通过电子掺杂,Tc可以升到约40 K区间;当生长在氧化物衬底上之后,Tc可以进一步升到约60 K区间.可见氧化物衬底的Ti-O八面体的构型在其Tc增强中具有不可或缺的作用,详细研究其晶格动力学对理解其超导增强机制具有重要的意义.

我们利用前述新型2D-HREELS谱仪测量了在SrTiO3衬底上生长的不同厚度FeSe薄膜的表面声子谱及其随温度的变化,并结合第一性原理计算研究了FeSe薄膜中磁有序对晶格动力学的影响[32].测量结果表明,FeSe的声子色散基本不会随着层厚的变化而发生改变,SrTiO3衬底的存在也不会影响FeSe薄膜的晶格动力学.结合表面德拜温度的测量结果,FeSe薄膜中由Fe原子和Se原子振动产生的声子在界面超导增强没有显著的作用,超导增强机制无法用传统的Baradeen-Cooper-Schrie ff er理论来解释.此外,磁相互作用一直以来被认为是铁基超导中的最重要的候选配对起源,然而,由于缺乏对单层薄膜磁有序的有效探测手段,单层FeSe薄膜中是否存在磁有序尚不明确.我们通过第一性原理计算与FeSe声子色散测量的结合,发现只有当FeSe薄膜中具有反铁磁自旋排列时,其计算的声子色散才能与HREELS测量结果相符合(见图6),说明磁相互作用在FeSe薄膜的超导中具有重要作用[32].

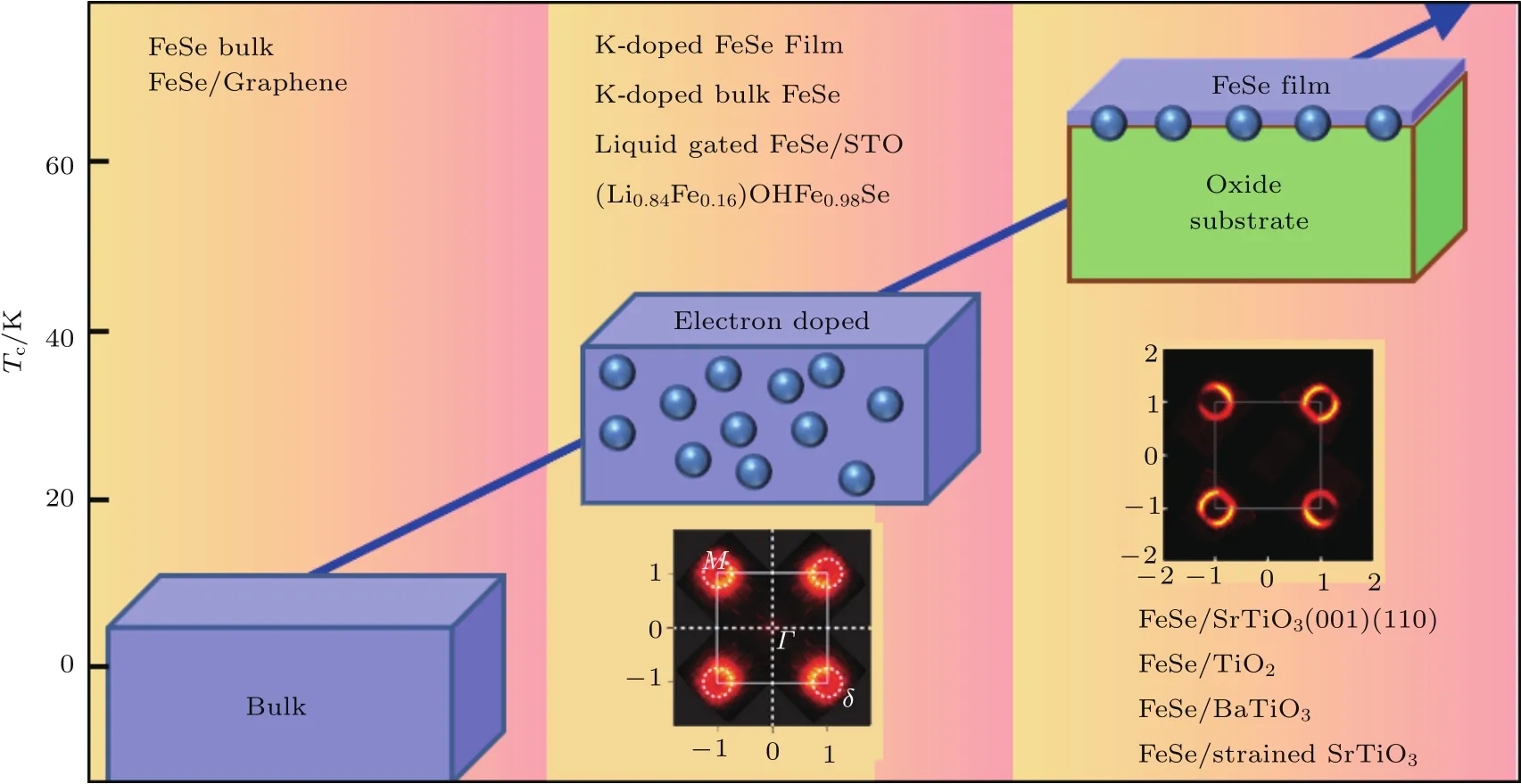
图5 FeSe体系超导Tc跳变示意图,其中FeSe体相Tc约8 K;通过电子掺杂,Tc可以升到约40 K区间;当生长在氧化物衬底上之后,Tc可以进一步升到约60 K区间Fig.5.Illustration of the Tcenhancement in FeSe systems.Tcof bulk FeSe is∼8 K.With electron doping,Tcof bulk FeSe can reach∼40 K.When single layer FeSe is grown on oxide substrate,Tccan be enhanced to∼60 K.

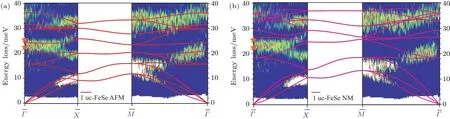
图6 单层薄膜中FeSe声子的2D-HREELS测量结果与理论计算的比较(经过美国物理学会的授权,图片摘自文献[32])(a)考虑FeSe晶格中反铁磁有序的情形;(b)不考虑FeSe晶格中磁序的情形;图中彩色的背底是2D-HREELS测得的声子强度分布,实线是理论计算的声子色散,桔色五角星表示拉曼散射测得的FeSe体相A1g(22.6 meV)和B1g(25.6 meV)声子模式[33]Fig.6.Comparison between experimental 2D-HREELS data and theoretical calculations for single-layer FeSe fi lms:(a)With checkerboard AFM spin con fi guration on Fe lattice;(b)without magnetic structure on Fe lattice.Coloured backgrounds are 2D-HREELS phonon intensity mapping,and solid lines are calculated phonon dispersion curves.Orange stars label the A1gmode(22.6 meV)and B1gmode(25.6 meV)measured by Raman scattering[33].The if gure was adapted from Ref.[32],copyright(2018)by the American Physical Society.

更重要的是,HREELS不仅可以观测到FeSe薄膜的声子模式,还能够观测到SrTiO3衬底的光学Fuchs-Kliewer(F-K)声子模式,即图7(a)中能量大于40 meV的模式.说明SrTiO3的F-K模式产生的偶极电场能够穿透FeSe薄膜,并且与FeSe薄膜中的电子发生较强的电子-声子耦合作用.特别地,F-K模式的强度随着FeSe膜厚度的增加呈指数衰减,与超导能隙随FeSe膜厚度的衰减规律完全一致,如图7(b)所示,说明衬底晶格振动与FeSe薄膜中电子的相互作用是FeSe/SrTiO3界面超导增强的关键[34].此外,通过对TiO2,BaTiO3等不同氧化物衬底的测量,发现这种F-K模式在氧化物中普遍存在[32],从而解释了在TiO2,BaTiO3以及SrTiO3(110)等衬底上生长的FeSe薄膜同样具有界面超导增强的原因.图7(c)形象地示意了氧化物衬底中的声子通过电场与FeSe薄膜中的电子相互作用的图像.然而衬底中的F-K模式在界面超导增强中的详细物理机制并不清楚,仍然需要后续相关工作的深入研究.

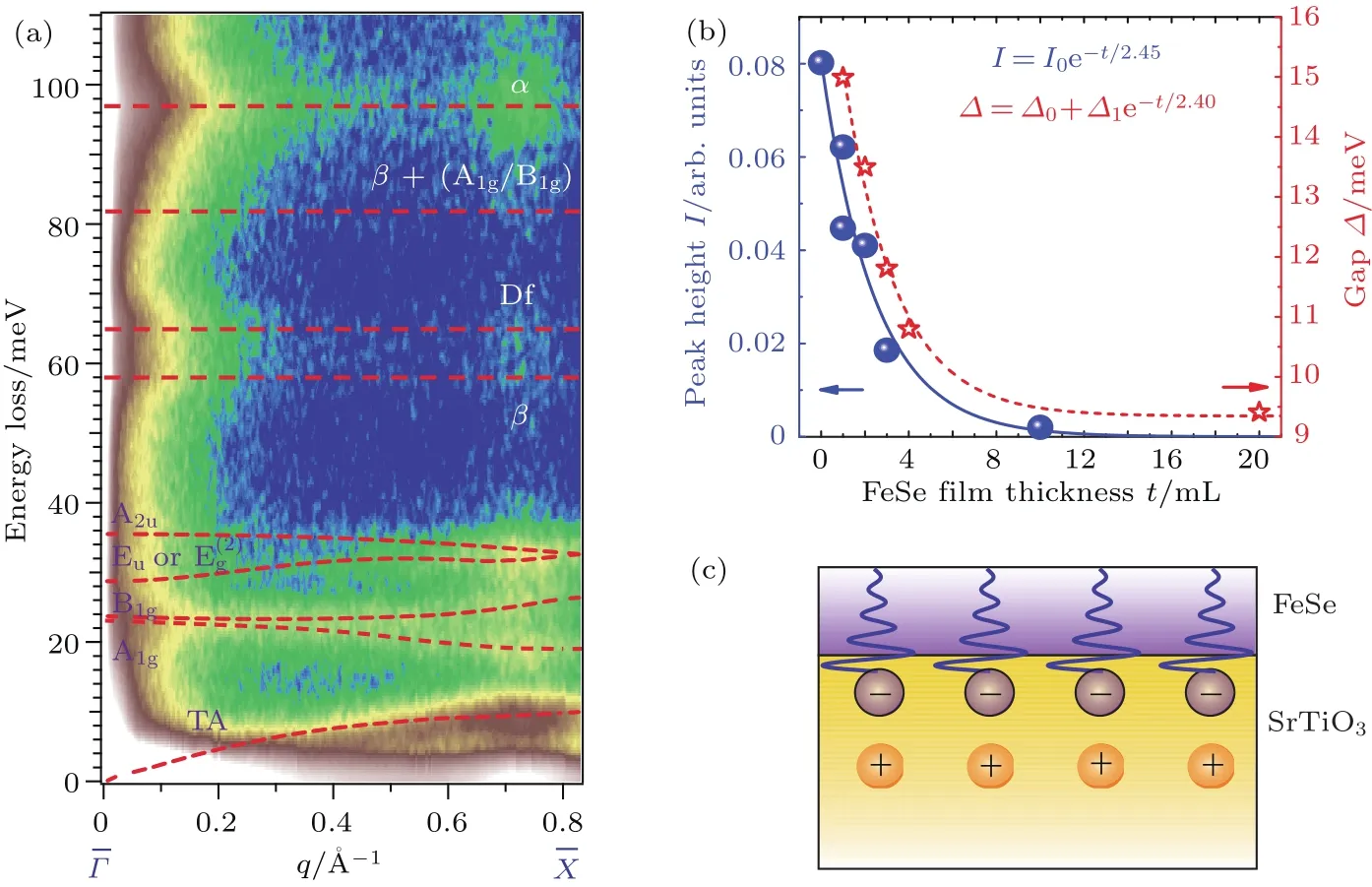
图7 (a)单层FeSe/SrTiO3体系的2D-HREELS测量结果,在低能端由FeSe贡献的声子(<40 meV)之外,还测到了衬底的光学支声子(>40 meV);(b)衬底中α模式的强度随厚度的变化及指数衰减拟合的结果;表面沉积K的FeSe/SrTiO3样品的超导能隙随厚度的变化及指数衰减拟合的结果,数据源自文献[35];(c)氧化物衬底中的声子通过电场与FeSe薄膜中的电子相互作用的示意图(经过美国物理学会的授权,图中(a)摘自文献[32],(b)摘自文献[34])Fig.7.(a)Energy-momentum mapping of 2D-HREELS measurements of 1uc-FeSe/SrTiO3samples,where red solid lines are guides to the eye;(b)plot and exponential fi tting of the peak height of the α mode as a function of the FeSe thickness(blue),plot and exponential fi tting of the superconducting gap size for the K-doped FeSe/SrTiO3as a function of the FeSe thickness(red),with data extracted from Ref.[35];(c)illustration of the penetration of the electric fi eld generated by the substrate oxide phonons into FeSe fi lms.The fi gure(a)was adapted from Ref.[32],and the fi gure(b)was adapted from Ref.[34],copyright(2018,2016)by the American Physical Society.

4 三维拓扑绝缘体表面的反常等离激元研究

在凝聚态物理学中,等离激元是最重要的元激发之一.1951年Pines和Bohm[36]预测提出等离激元的概念,用于描述在固体当中由于库仑相互作用产生的电荷密度集体振荡的元激发.1957年,Ritchie[37]又将等离激元的概念延伸到表面和界面上,指出了表面等离激元的存在.自此之后,科学家对于等离激元性质的研究持续了60年之久并仍在发展壮大,由此逐渐衍生出等离子体光子学这一前沿领域及其他诸多交叉应用领域.对于任何可能的应用,最为重要的问题就是等离激元的寿命.在普通材料体系中,等离激元通常只能存在于很小的动量范围,因为当它的色散进入电荷空穴连续区时,就会转化为单粒子激发从而导致其寿命的急剧衰减[38,39].此外,一般材料中,杂质散射也是必然的另一种衰减通道.这种急剧衰减是几乎所有等离激元的普遍特征,无论它是来自普通金属中具有抛物线型色散的有质量电子[40],还是来自于石墨烯等材料中具有线性色散的无质量狄拉克电子[41].对于拓扑非平庸的狄拉克电子形成的等离激元又会是怎样的呢?一个典型的例子是在三维拓扑绝缘体的表面态上,由于动量和自旋的锁定使得表面态电子免受任何非磁性杂质的背散射[42,43]从而拥有更长的寿命,那么它所形成的集体模式也会具有很长的寿命吗?在拓扑绝缘体中关于等离激元的理论和实验工作发展迅速[44−51],但尚无关于其长寿命方面的实验观测报道.

我们选取典型的三维拓扑绝缘体Bi2Se3,利用前述2D-HREELS谱仪详细研究了三维拓扑绝缘体表面等离激元的色散和衰减特征[52],结果如图8所示.研究发现,三维拓扑绝缘体Bi2Se3表面态产生一支反常的声学支等离激元模式,其色散关系在一个很大的动量范围(至少到第二布里渊区中心)呈现出几乎线性的行为,并且不依赖于晶格的周期性;通过对磁性原子Mn掺杂的Bi2Se3的对比实验,发现这支模式与狄拉克锥有同生同灭的特性,于是在实验上指认出这支模式是来自狄拉克电子的声学支等离激元;这支模式无论是在电荷空穴连续区内或外都呈现出弱衰减的特性,说明拓扑保护不仅仅可以出现在单电子层面,对于集体模式也是适用的;这支模式的能量色散比以往任何理论预测[44,45]的都要低,并且与一支表面声子[53,54]的能量接近,暗示着它和声子之间可能存在很强的相互作用[52].

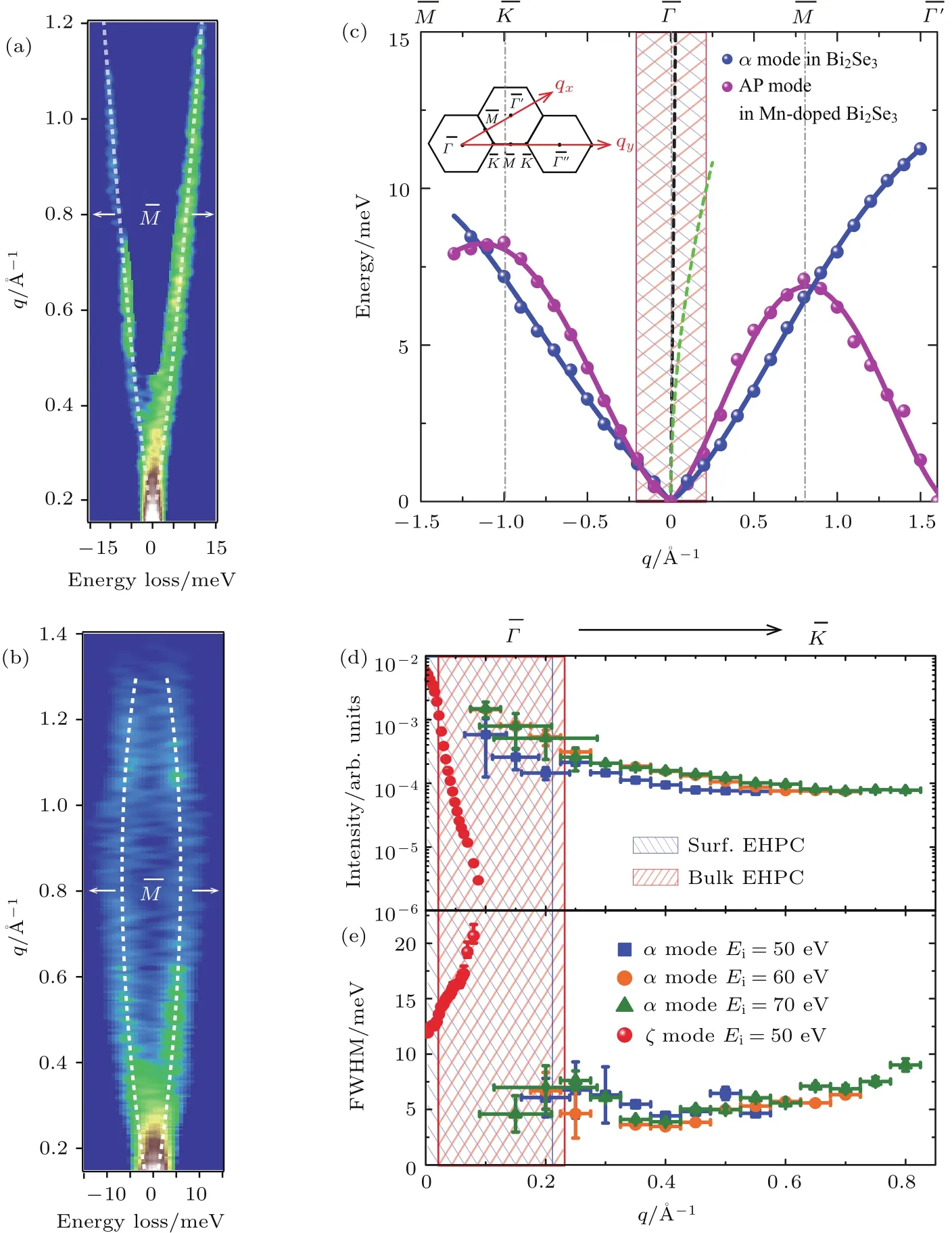
图8 Bi2Se3表面声学等离激元测量结果示意图(经过美国物理学会的授权,图片摘自文献[52]) (a)Mn掺杂Bi2Se3中声学支声子(AP模式)的2D-HREELS测量结果;(b)Bi2Se3中声学支等离激元(α模式)的2D-HREELS测量结果;(c)Bi2Se3中α模式和Mn掺杂Bi2Se3中AP模式的色散关系,阴影部分表示电子-空穴连续区;(d),(e)分别为Bi2Se3中α模式的归一化强度与线宽,体相等离激元(ζ模式)的结果用于对比表明其寿命与受拓扑保护的声学支等离激元明显不同Fig.8.(a)2D-HREEL mapping of the acoustic phonon(AP mode)of Mn-doped Bi2Se3;(b)2D-HREEL mapping of the acoustic plasmon(α mode)of Bi2Se3;(c)the dispersions of the acoustic plasmon(α mode)of Bi2Se3,and the acoustic phonon(AP mode)of Mn-doped Bi2Se3,and the shaded zones label the electron-hole pairing continuum of massless Dirac electrons and normal bulk conducting electrons;(d)the normalized intensity and(e)FWHM of the α mode of Bi2Se3with di ff erent incident energies.The normalized intensity and FWHM of the bulk plasmon(ζ mode)of Bi2Se3are also plotted for comparison.The fi gure was adapted from Ref.[52],copyright(2017)by the American Physical Society.

5 结 论

本文详细介绍了能够对电子能量、动量做二维成像探测分析的新型高分辨电子能量损失谱仪的设计思路、研制要点及性能指标,特别是重点描述了其在表面准粒子动量分辨测量方面所具有的优势.该谱仪在FeSe/SrTiO3界面超导体系的晶格动力学测量上取得了一系列重要的结果,特别是阐明了衬底声子在界面超导增强中的关键作用.此外,利用该谱仪还发现了拓扑绝缘体表面受拓扑保护的声学支等离激元,将拓扑保护的概念推广到了集体激发准粒子中.充分发挥新型电子能量损失谱仪观测表面元激发分辨率高、动态范围大的优势,将有力地推动凝聚态物理问题研究的深入和发展.

[1]Egerton R F 2011 Electron Energy-Loss Spectroscopy in the Electron Microscope(3rd Ed.)(New York:Springer US)pp1–26

[2]Lagos M J,Trugler A,Hohenester U,Batson P E 2017 Nature 543 529

[3]Ibach H,Mills D L 1982 Electron Energy Loss Spectroscopy and Surface Vibrations(New York:Academic Press)pp1–20

[4]Qin H J,Shi J R,Cao Y W,Wu K H,Zhang J D,Plummer E W,Wen J,Xu Z J,Gu G D,Guo J D 2010 Phys.Rev.Lett.105 256402

[5]Kogar A,Rak M S,Vig S,Husain A A,Flicker F,Joe Y I,Venema L,Macdougall G J,Chiang T C,Fradkin E 2017 Science 358 1314

[6]Zhu X,Cao Y,Zhang S,Jia X,Guo Q,Yang F,Zhu L,Zhang J,Plummer E W,Guo J 2015 Rev.Sci.Instrum.86 083902

[7]LK-Technologies http://www.lktech.com/products/els-5000.php[2018-4-12]

[8]SPECS http://www.specs.de/cms/front_content.php?idart=134[2018-4-12]

[9]Valla T,Fedorov A V,Johnson P D,Wells B O,HulbertS L,Li Q,Gu G D,Koshizuka N 1999 Science 285 2110

[10]Damascelli A,Hussain Z,Shen Z X 2003 Rev.Mod.Phys.75 473

[11]Fadley C S 2010 J.Electron Spectrosc.Relat.Phenom.178 2

[12]Ibach H 1991 Electron Energy Loss Spectrometers-The Technology of High Performance(Vol.63)(Berlin:Springer-Verlag)pp131–146

[13]Wang Q,Li Z,Zhang W,Zhang Z,Zhang J,Li W,Ding H,Ou Y,Deng P,Chang K,Wen J,Song C,He K,Jia J,Ji S,Wang Y,Wang L,Chen X,Ma X,Xue Q 2012 Chin.Phys.Lett.29 037402

[14]Hsu F C,Luo J Y,Yeh K W,Chen T K,Huang T W,Wu P M,Lee Y C,Huang Y L,Chu Y Y,Yan D C 2008 Proc.Natl.Acad.Sci.USA 105 14262

[15]Bozovic I,Ahn C 2014 Nat.Phys.10 892

[16]Wang L,Ma X,Xue Q 2016 Supercond Sci.Technol.29 123001

[17]Wang Z,Liu C,Liu Y,Wang J 2017 J.Phys.:Condens.Matter 29 153001

[18]Huang D,Ho ff man J E 2017 Annual Rev.Condens.Matter Phys.8 311

[19]Shiogai J,Ito Y,Mitsuhashi T,Nojima T,Tsukazaki A 2016 Nat.Phys.12 42

[20]Lei B,Cui J H,Xiang Z J,Shang C,Wang N Z,Ye G J,Luo X G,Wu T,Sun Z,Chen X H 2016 Phys.Rev.Lett.116 077002

[21]Hanzawa K,Sato H,Hiramatsu H,Kamiya T,Hosono H 2016 Proc.Natl.Acad.Sci.USA 113 3986

[22]Miyata Y,Nakayama K,Sugawara K,Sato T,Takahashi T 2015 Nat.Mater.14 775

[23]Wen C H P,Xu H C,Chen C,Huang Z C,Lou X,Pu Y J,Song Q,Xie B P,Abdel-Ha fi ez M,Chareev D A,Vasiliev A N,Peng R,Feng D L 2016 Nat.Commun.7 10840

[24]Lu X F,Wang N Z,Wu H,Wu Y P,Zhao D,Zeng X Z,Luo X G,Wu T,Bao W,Zhang G H,Huang F Q,Huang Q Z,Chen X H 2015 Nat.Mater.14 325

[25]Zhao L,Liang A,Yuan D,Hu Y,Liu D,Huang J,He S,Shen B,Xu Y,Liu X,Yu L,Liu G,Zhou H,Huang Y,Dong X,Zhou F,Liu K,Lu Z,Zhao Z,Chen C,Xu Z,Zhou X J 2016 Nat.Commun.7 10608

[26]Lee J J,Schmitt F T,Moore R G,Johnston S,Cui Y T,Li W,Yi M,Liu Z K,Hashimoto M,Zhang Y,Lu D H,Devereaux T P,Lee D H,Shen Z X 2014 Nature 515 245

[27]Zhang P,Peng X L,Qian T,Richard P,Shi X,Ma J Z,Fu B B,Guo Y L,Han Z Q,Wang S C,Wang L L,Xue Q K,Hu J P,Sun Y J,Ding H 2016 Phys.Rev.B 94 104510

[28]Zhou G,Zhang D,Liu C,Tang C,Wang X,Li Z,Song C,Ji S,He K,Wang L,Ma X,Xue Q 2016 Appl.Phys.Lett.108 202603

[29]Ding H,Lü Y,Zhao K,Wang W,Wang L,Song C,Chen X,Ma X,Xue Q 2016 Phys.Rev.Lett.117 067001

[30]Rebec S N,Jia T,Zhang C,Hashimoto M,Lu D H,Moore R G,Shen Z X 2017 Phys.Rev.Lett.118 067002[31]Peng R,Xu H C,Tan S Y,Cao H Y,Xia M,Shen X P,Huang Z C,Wen C H P,Song Q,Zhang T,Xie B P,Gong X G,Feng D L 2014 Nat.Commun.5 5044

[32]Zhang S,Guan J,Wang Y,Berlijn T,Johnston S,Jia X,Liu B,Zhu Q,An Q,Xue S,Cao Y,Yang F,Wang W,Zhang J,Plummer E W,Zhu X,Guo J 2018 Phys.Rev.B 97 035408

[33]Gnezdilov V,Pashkevich Y G,Lemmens P,Wulferding D,Shevtsova T,Gusev A,Chareev D,Vasiliev A 2013 Phys.Rev.B 87 144508

[34]Zhang S,Guan J,Jia X,Liu B,Wang W,Li F,Wang L,Ma X,Xue Q,Zhang J,Plummer E W,Zhu X,Guo J 2016 Phys.Rev.B 94 081116

[35]Zhang W H,Liu X,Wen C H P,Peng R,Tan S Y,Xie B P,Zhang T,Feng D L 2016 Nano Lett.16 1969

[36]Pines D,Bohm D 1952 Phys.Rev.85 338

[37]Ritchie R H 1957 Phys.Rev.106 874

[38]Landau L 1957 Soviet Physics Jetp-Ussr 3 920

[39]Pines D,Nozières P 1966 The Theory of Quantum Liquids:Normal Fermi Liquids(Vol.1)(New York:Benjamin Inc.)

[40]Ninham B W,Powell C J,Swanson N 1966 Phys.Rev.145 209

[41]Liu Y,Willis R F,Emtsev K V,Seyller T 2008 Phys.Rev.B 78 201403

[42]Roushan P,Seo J,Parker C V,Hor Y S,Hsieh D,Qian D,Richardella A,Hasan M Z,Cava R J,Yazdani A 2009 Nature 460 1106

[43]Zhang T,Cheng P,Chen X,Jia J F,Ma X,He K,Wang L,Zhang H,Dai X,Fang Z,Xie X,Xue Q K 2009 Phys.Rev.Lett.103 266803

[44]Das Sarma S,Hwang E H 2009 Phys.Rev.Lett.102 206412

[45]Raghu S,Chung S B,Qi X L,Zhang S C 2010 Phys.Rev.Lett.104 116401

[46]Kogar A,Vig S,Thaler A,Wong M H,Xiao Y,Reig I P D,Cho G Y,Valla T,Pan Z,Schneeloch J,Zhong R,Gu G D,Hughes T L,MacDougall G J,Chiang T C,Abbamonte P 2015 Phys.Rev.Lett.115 257402

[47]Di Pietro P,Ortolani M,Limaj O,Di Gaspare A,Giliberti V,Giorgianni F,Brahlek M,Bansal N,Koirala N,Oh S,Calvani P,Lupi S 2013 Nat.Nano 8 556

[48]Autore M,Engelkamp H,D’Apuzzo F,Gaspare A D,Pietro P D,Vecchio I L,Brahlek M,Koirala N,Oh S,Lupi S 2015 ACS Photon.2 1231

[49]Politano A,Silkin V M,Nechaev I A,Vitiello M S,Viti L,Aliev Z S,Babanly M B,Chiarello G,Echenique P M,Chulkov E V 2015 Phys.Rev.Lett.115 216802

[50]Glinka Y D,Babakiray S,Johnson T A,Holcomb M B,Lederman D 2016 Nat.Commun.7 13054

[51]Zhang F,Zhou J,Xiao D,Yao Y 2017 Phys.Rev.Lett.119 266804

[52]Jia X,Zhang S Y,Sankar R,Chou F C,Wang W H,Kempa K,Plummer E W,Zhang J D,Zhu X T,Guo J D 2017 Phys.Rev.Lett.119 136805

[53]Zhu X,Santos L,Sankar R,Chikara S,Howard C,Chou F C,Chamon C,El-Batanouny M 2011 Phys.Rev.Lett.107 186102

[54]Zhu X,Santos L,Howard C,Sankar R,Chou F C,Chamon C,El-Batanouny M 2012 Phys.Rev.Lett.108 185501