利用单轴压强下的电阻变化研究铁基超导体中的向列涨落∗

李世亮1)2)† 刘曌玉1)2) 谷延红1)2)

1)(中国科学院物理研究所,北京凝聚态物理国家研究中心,北京 100190)

2)(中国科学院大学物理科学学院,北京 100049)

(2018年4月9日收到;2018年4月26日收到修改稿)

1 引 言

高温超导体(此处特指铜氧化合物超导体)被发现已经30余年,但是其机理仍然没有获得超导界的共识[1].铁基超导体的发现为解决高温超导机理提供了一个契机.除了其超导临界温度较高之外,铁基超导材料也是层状的,且可以认为超导态与反铁磁序比邻,和铜氧化合物超导体很相似[2].当然,铁基超导体也呈现出很多独特的性质.例如,其反铁磁母体是坏金属,而铜氧化合物的母体通常被认为是莫特绝缘体[2].再如,铁基超导态的配对对称性大部分为s波,而铜氧化合物超导态的对称性则基本被认为是d波[2].本文所重点涉及到的“电子向列相”,也体现了两者之间较大的不同.

所谓电子向列相,是与液晶体系中的向列相类比而提出的概念.在棒状分子组成的液晶体系中,其分子的不同排布,会形成不同的相,从而导致迥然不同的物理性质.这些液晶相包括液体、晶体、近晶相和向列相等,可以通过对称性的概念来理解[3].在晶体中,棒状分子完全规则排列,和液体相比,既破坏了平移对称性,也破坏了旋转对称性.在向列相中,棒状分子的位置随机分布,其方向则指向某一方向,因此保留了平移对称性,而破坏了旋转对称性.与向列相相比,近晶相进一步破坏了某些平移对称性,但并不像晶体那样完全有序.借助这些概念,Kivelson等[4]提出了电子液晶相的概念,其晶体、液体和近晶相分别对应了电子晶体、各向同性电子液体以及条纹相,而向列相则对应了破坏晶格旋转对称性但保留其平移对称性的电子相,可以简单地认为是条纹相融化并涨落的结果.这一概念的引入是从莫特绝缘体出发,考虑电子之间的强关联作用而导入的.而实际上,电子向列相也可以从弱关联角度出发,考虑到Pomeranchuk不稳定性,导致费米面的形状破坏了晶格的旋转对称性,从而呈现出较强的各向异性[5].不管以哪种角度出发去理解,电子向列相本质上可以仅从对称性的角度去定义.

铁基超导体中的电子向列相呈现出一些独有的特点.在铜氧化合物超导体中,通常认为,向列相存在于赝隙内部,其面内各向异性在电阻、Nernst、中子散射、扫描隧道显微镜谱等测量中可观测到,但信号较弱[6−9].向列相存在的温度低于四方到正交的结构相变的温度,即面内晶格本身的旋转对称性其实在向列相发生之前就已经从四重(C4)降低到(C2).在铁基超导体中,向列相的转变则与晶格的四方到正交结构相变同时发生,其原因来源于电子和晶格之间的耦合[10].同样,向列相所导致的各向异性可以通过电阻、中子散射和角分辨光电子谱等手段观测到[11−13].目前,铁基超导体中向列相的来源大致可以分为两类理论[10],分别基于自旋和轨道自由度.由于二者之间的强耦合,对于哪一种自由度在形成向列相中是主要驱动力还没有取得共识.

本文将不讨论向列相的来源,而是集中介绍近几年我们在研究向列相与反铁磁和超导之间的关系上所取得的一些成果.接下来,首先介绍我们自主研发的一种小型单轴压力装置,可以以很高的精度研究电阻随单轴压强的变化,从而获得向列涨落的信息.随后,主要介绍针对BaFe2−xNixAs2体系中向列量子临界点(QCP)的研究[14]以及对反铁磁有序磁矩大小和向列涨落强度之间关系的研究,并提出了铁基超导体统一的相图[15].最后给出结论和展望.

2 单轴压力装置简介

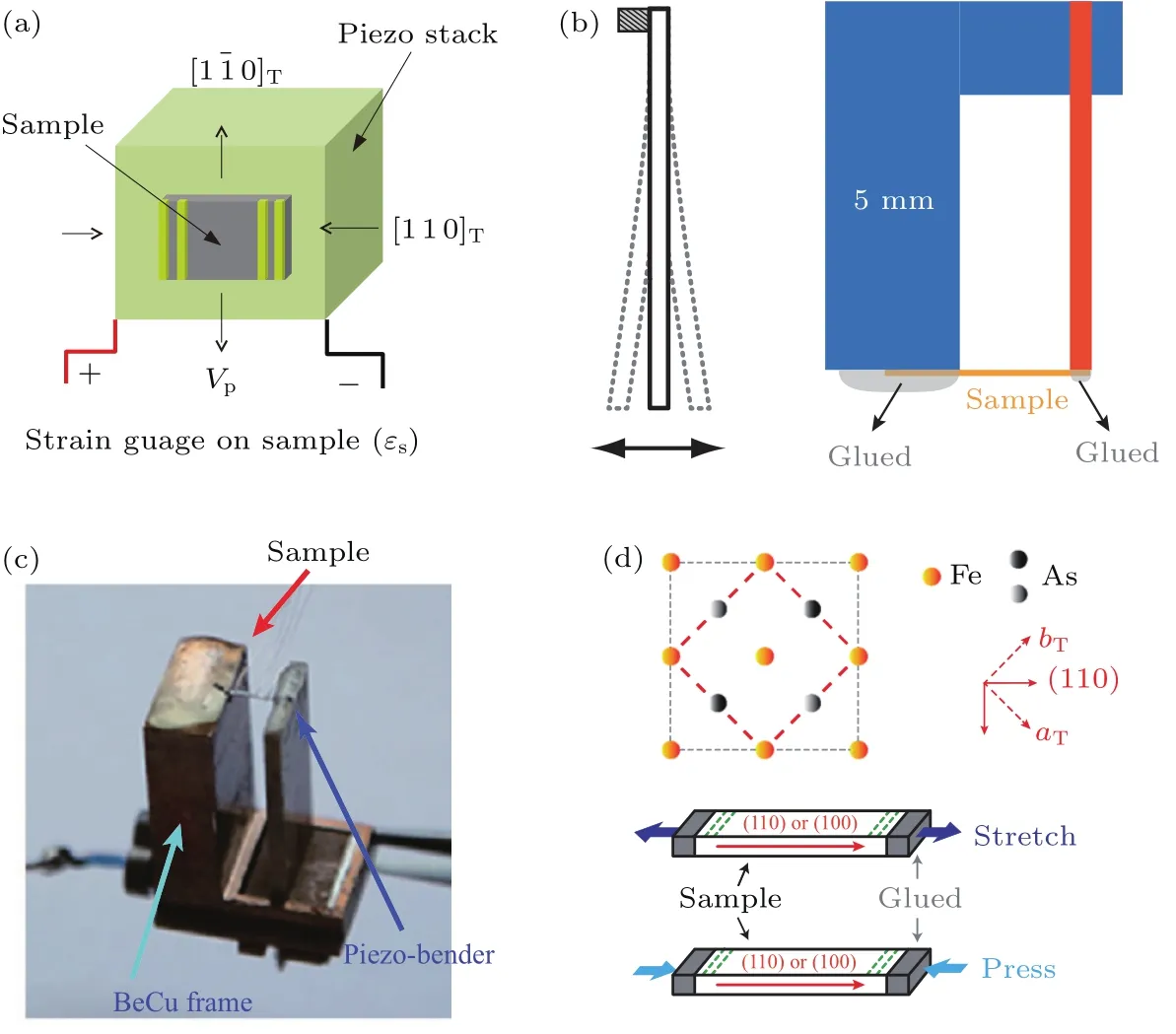
图1 (a)利用压电陶瓷堆测量电阻随应变变化的装置示意图[16](控制压电陶瓷伸缩的电压为Vp,样品在(1¯10)方向伸长时也会在(110)方向缩短);(b)左侧为固定一端时压电陶瓷片随控制电压变化而顶端左右移动的示意图,右侧为本文使用的单轴压强装置示意图;(c)单轴压强装置实物图,其中支架为铍铜[14];(d)铁基超导体铁砷层俯视图及各方向的定义[14]Fig.1.(a)Schematic diagram of the piezo stack device for measuring the strain dependence of the resistivity[16].The voltage to control the stretch of the piezo stack is Vp.The sample becomes shorter along the(110)direction when it is stretched along the(1¯10)direction.(b)(left)Schematic diagram showing the movement of the bottom of the piezo bender with the change of voltage when its top is fi xed.(right)Schematic diagram of the uniaxial pressure device used in this manuscript.(c)The photo of the uniaxial pressure device,where the frame is BeCu[14].(d)Top view of the FeAs layers in iron-based superconductors and the de fi nitions of di ff erent directions[14].

铁基超导体的向列相可以认为是一种伊辛形式的向列序[10],其序参量沿着正交结构a或b方向(即Fe—Fe方向),与反铁磁序的方向一致.在结构相变(即向列相相变)温度Ts之下,晶格存在着孪晶结构,因此很难测量这两个方向的各向异性.此时,可以通过沿Fe—Fe方向施加单轴压强来退孪晶,从而分别测量正交结构a和b方向的性质[11].在Ts之上,可以认为向列涨落在两个方向幅度相同,而沿Fe—Fe方向施加压强则可以诱导出各向异性,从而获得向列极化率的信息[16].这可以类比于在顺磁态测量磁矩随磁场的变化,从而获得磁化率的过程.在早期的测量中,样品贴在压电陶瓷堆上,通过压电陶瓷堆的伸缩,测量电阻随应变的变化,如图1(a)所示.这种方法的缺点在于,样品完全被树脂胶所覆盖,因此会导致较大的应力不均匀性,从而影响测量精度.

我们为此研制了一款基于压电陶瓷片的单轴压强装置,可放置于物性测量系统中进行电阻测量.在压电陶瓷底部固定时,其顶部可以随电压正负而左右移动,如图1(b)中左图所示.如果将其顶部固定,使其无法移动,则会对外输出力,如图1(b)中右图所示.对于具体的某一样品,可以通过劳厄X射线仪定向,然后利用线切割沿着需要施加单轴压强的方向将样品切成长方形,并用环氧树脂胶黏在压电陶瓷片的顶部和旁边的铍铜支架上,如图1(c)所示.这一装置可以在低温下原位改变压力,且其压强可以正也可以负(这里正压强指压缩样品),因此在改变压强时一定会经过零点,非常适合测量零压附近的性质,如下面将要谈到的向列极化率.而且,样品中间是没有胶的,从而避免了残余应力的影响,提高了测量精度.这一设计可以测量较薄样品(微米厚度),这对于很多无法生长大单晶的材料非常重要.在具体测量上,单轴压强将沿着四方相(110)和(100)的方向,分别对应Fe—Fe和Fe—As—Fe的方向,如图1(d)所示,其中前者为低温下向列序的方向.该装置的缺点之一是暂时还无法精确给出单轴压强的大小.目前,我们是通过比较在该装置上与采用弹簧施加压力装置上同一样品的电阻的结果[12]而估计出压力.具体压强值则通过标定后的压力除以样品的截面积来获得.另外,当样品很薄或压强太大时,样品在压时可能会出现弯曲,从而导致压与拉两个过程的电阻变化不对称,此时适当减小压强可避免这一情况的发生.

3 BaFe2−xNixAs2中的向列QCP

如同很多其他序在零温下随着某一非热学量改变可能会发生量子临界相变一样,向列序也被认为可能存在着QCP,与其相关的量子涨落也可能会增强甚至诱导出超导[17−19].然而,之前一些报道认为可能存在量子临界涨落的大部分证据仅限于Ts在某一温度下变为零,以及向列极化率在可能的QCP处当温度趋于零度时呈现出发散的行为[16,20−24].需要指出的是,前者并不能保证存在QCP,因为该量子相变也可能为一级的.而对于后者,向列极化率随温度呈居里-外斯行为,这和欠掺区域是一样的,都可以用朗道二级相变理论很好地解释,使得我们无法有效地区分向列热涨落和量子涨落.另外,在有QCP的系统中,量子涨落区除了在欠掺区与有序区存在过渡行为外,在过掺区也应该与低温的无序区存在着过渡行为[25],而后者在有向列QCP的铁基超导材料中还未被观测到.这些问题制约了我们对向列量子临界相变的理解.

为此,我们对BaFe2−xNixAs2这一系统中的向列极化率进行了系统性的研究.该体系中的反铁磁和向列序在x≈0.1处消失,同时也到达超导态的最佳掺杂.图2(a)给出了母体BaFe2As2中沿(110)方向电阻随压强的变化.在高温下,电阻随压力增加而上升,这与正常金属在单轴压强下长度减小而导致电阻下降是相反的,表明了向列涨落的影响.数据中对称的回滞是由于压电陶瓷片的铁电回滞所导致的,在处理中则取升降压的平均值来消除该回滞的影响.定义电阻变化∆R=R(p)−R0,其中R(p)和R0分别为压强p下的电阻和零压下的电阻.随后定义ζ=d(∆R/R0)/dp,对应了归一电阻随压强的变化,也就是图2(a)中的斜率.随着温度降低,母体中ζ逐渐增加,并在130 K出现了类似铁磁的行为,很可能来源于Ts之下孪晶的生成.

图2(b)给出了欠掺杂样品到略微过掺杂样品的ζ随温度的变化.在Ts以上,可以用下述类似居里-外斯公式来描述其行为:

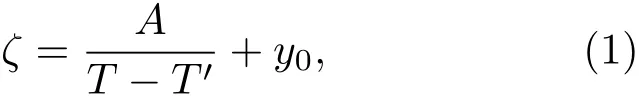
其中A,T′和y0均为常数.与以前的报道相比较[16],这表明ζ正比于向列极化率.T′对应平均场情况下的向列转变温度.在具有结构相变的样品中,T′小于真正的相变温度Ts,通常被认为是来源于向列序与晶格之间的耦合[16].图2(c)给出了过掺样品的数据,与欠掺样品很不相同的是在Th处出现了一个鼓包,与弹性模量测试中观测到的行为类似[21],表明向列涨落和晶格之间的耦合在极度过掺杂区域中也依然存在.

我们还测量了单轴压强施加在(100)方向的数据.让人惊讶的是,在该方向依然可观测到与(110)方向相同的电阻变化,尽管其幅度小了很多,如图2(d)所示.如同前面所分析的,电阻随压强的变化与普通金属行为是相反的,表明在该方向可能仍然存在着向列涨落的影响.值得注意的是,斜率最大的样品是x=0.11.通过同样的方法,在图2(e)中给出了沿(100)方向ζ(100)随温度的变化,其值确实是在x=0.11掺杂处最强.在过掺杂区,也可以观测到鼓包的行为,且其温度与(110)方向数据所定的Th是基本一致的.我们将过掺杂区两个方向的数据外推到零温,可以获得零温下ζ随掺杂的变化,如图2(f)所示.可以看出,ζ(110)一直比ζ(100)大一个量级.更重要的是,它们在趋近x=0.11处都存在着发散行为,与零温向列极化率趋近向列QCP时应出现发散行为是一致的.

图3(a)和图3(b)分别给出了沿(110)和(100)方向ζ的强度,其中前者由于变化很大而采用了对数坐标.可以看出,向列涨落位于整个超导和反铁磁区域之上,一直到不超导的极度过掺杂区域(x>0.2)仍然存在,表明向列涨落对超导相和反铁磁相都很重要.通过(1)式拟合的平均场转变温度T′在x约为0.11处变为零,说明如果有向列QCP,应当位于该处.对于典型的QCP系统,其量子涨落应当和有序区的热涨落与无序区的涨落都存在着区别[25].我们在过掺杂区域所观测到的鼓包温度Th随掺杂反推到零值所对应的掺杂浓度x也位于0.11,符合量子涨落与无序区涨落之间的过渡的预期.但是在(110)方向,我们无法确定量子涨落的区域,因为热涨落的信号太强.而在(100)方向,则可以清楚地看到ζ在x=0.11处是最强的,表明其与量子涨落是相关的.

在(100)方向观测到向列涨落是超出预期的,因为铁基超导体中的向列序被认为是伊辛类型,即只出现在(110)方向.我们的结果可能来源于铁基超导体是一个巡游体系,其准粒子的性质和序参量的动力学在QCP附近都可能发生巨大改变.已有蒙特卡罗的理论模拟表明,在金属的QCP附近,其量子临界向列涨落会有较高的各向同性[26].因此,电阻随单轴压强的变化可能在QCP处也表现出一定程度的各向同性,从而导致在(100)方向也观测到向列涨落的信号.另外也不能排除在QCP附近可能存在着更高的对称性,如同在一维横场伊辛模型中所观测到的情形[27].

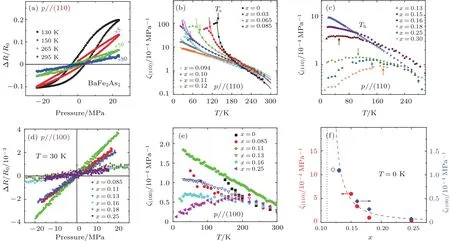
图2 (a)BaFe2As2中电阻随沿(110)方向单轴压强的变化[14];(b),(c)欠掺和过掺区域(110)方向ζ随温度的变化[14];(d)电阻随沿(100)方向单轴压强的变化[14];(e)沿(100)方向ζ随温度的变化[14];(f)零温下ζ随掺杂的变化[14]Fig.2.(a)The uniaxial pressure dependence of the resistance in BaFe2As2along the(110)direction[14];(b),(c)the temperature dependence of ζ along the(110)direction in underdoped and overdoped samples[14];(d)the uniaxial pressure dependence of the resistance along the(100)direction[14];(e)the temperature dependence of ζ along the(100)direction[14];(f)the doping dependence of ζ at zero temperature[14].

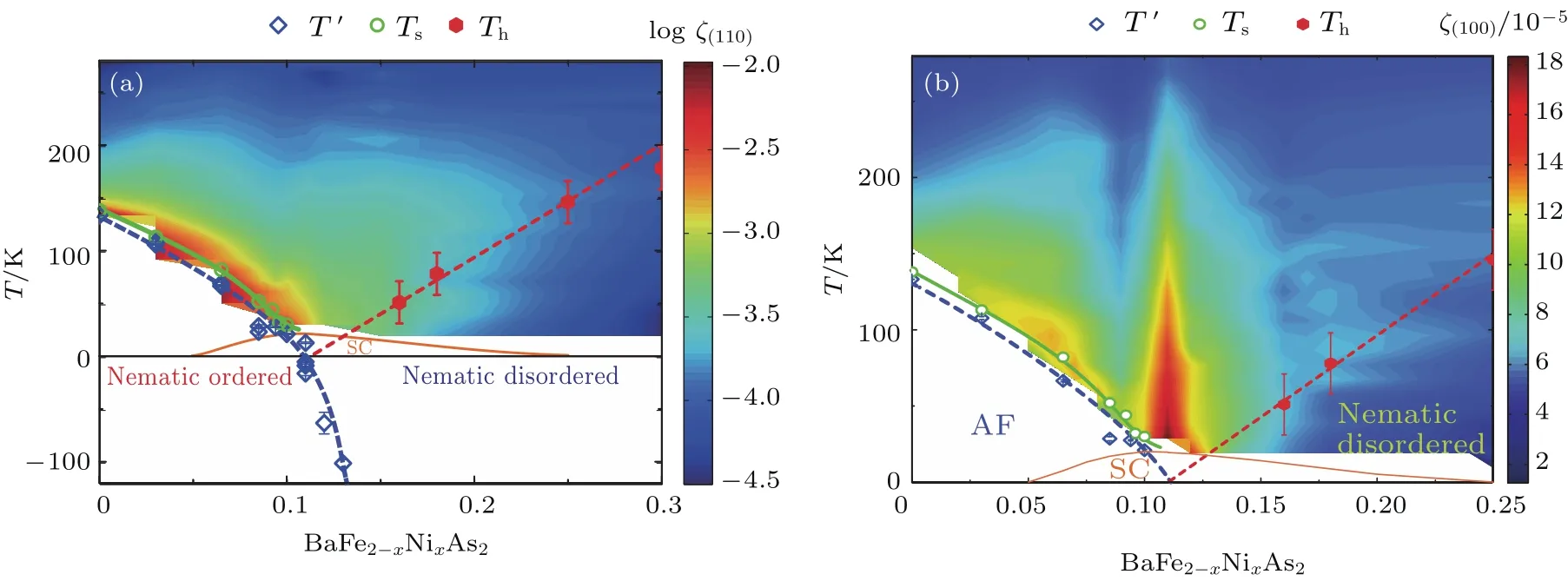
图3 BaFe2−xNixAs2的相图[14] (a)和(b)的彩图分别为单轴压强沿(110)和(100)方向的ζ,其中(a)采用了对数坐标;T′,Ts和Th分别对应居里-外斯拟合的平均场转变温度、结构相变温度以及过掺杂区域ζ的鼓包温度Fig.3.Phase diagram of BaFe2−xNixAs2[14]:The colormaps in(a)and(b)are ζ for the uniaxial pressure along the(110)and(100)directions,where that in(a)has used the logarithmic scale.T′,Tsand Thcorrespond to the mean- fi eld transition temperature in the Curie-Weiss fi tting,the structural transition temperature and the hump temperature of ζ in overdoped regime.

4 铁基超导体统一相图

在研究铁基超导体时,人们通常也采用了和铜基超导体中类似的术语,例如“母体”、“空穴”或“电子”掺杂等.但是仔细考察可以获知,实际上这些称呼在铁基超导体中并不准确.首先,铁基超导体中所谓“母体”的有序磁矩差异非常大[28].在“1111”体系中,简单的稀土元素置换会导致几倍的有序磁矩变化.在NaFeAs中,不但磁矩很小,且能够发现超导电性,尽管其超导不是体超导.而类似于LiFeAs和FeSe这种并不含有明显掺杂的材料,没有反铁磁长程序且之间出现了超导.实验上,尚未发现各类材料上有序磁矩变化的规律性.换句话说,暂时只能列出一个表格来显示各类“母体”材料有序磁矩的不同.其次,铁基超导电性不仅可以通过空穴或电子掺杂来获得,也可以通过所谓“等价”掺杂来获得[29],表明载流子在其中的作用很复杂.这些在母体和掺杂材料中巨大的分歧使得我们很难获得铁基材料低能物理的统一图像,只能根据具体材料来理解反铁磁和超导的性质.

如前所述,铁基超导体中除了反铁磁序和超导态之外,还存在着向列相.因此,我们对多类铁基超导体母体进行了单轴压强的测量,从而获得了其向列极化率.图4给出了多种材料的|χn|−1的温度依赖关系,其中χn定义为ζ(110)−y0,而取绝对值是因为在有些材料中ζ(110)是负的.所有数据都遵循(1)式的行为,|χn|−1也都和温度成线性关系,因此可以通过拟合获得向列居里常数A.需要指出的是,由于一些材料的单晶很小,会导致较大的误差,因此我们都测量了几次来计算A的均值及其标准偏差.由于A是通过电阻测量来获得的,还需要考虑费米面的效应.为此我们引入一个无量纲的参数κ,其值为(|νΓF|+|νMF|)2并与BaFe2As2中该值归一.其中νΓF和νMF是结构相变温度Ts之上两个近乎嵌套的空穴和电子费米口袋在费米面处的费米速度.这一形式来源于脏极限下的自旋涨落散射[30],其电阻各向异性正比于电子和空穴口袋Φ函数的差异的平方.依据定义,Φ函数是费米速度沿电场的投影.需要指出的是,输运理论是近似且复杂的,这里强调κ是作为唯象的参数引入的,而非成熟的理论结果.此处定义An=κA.

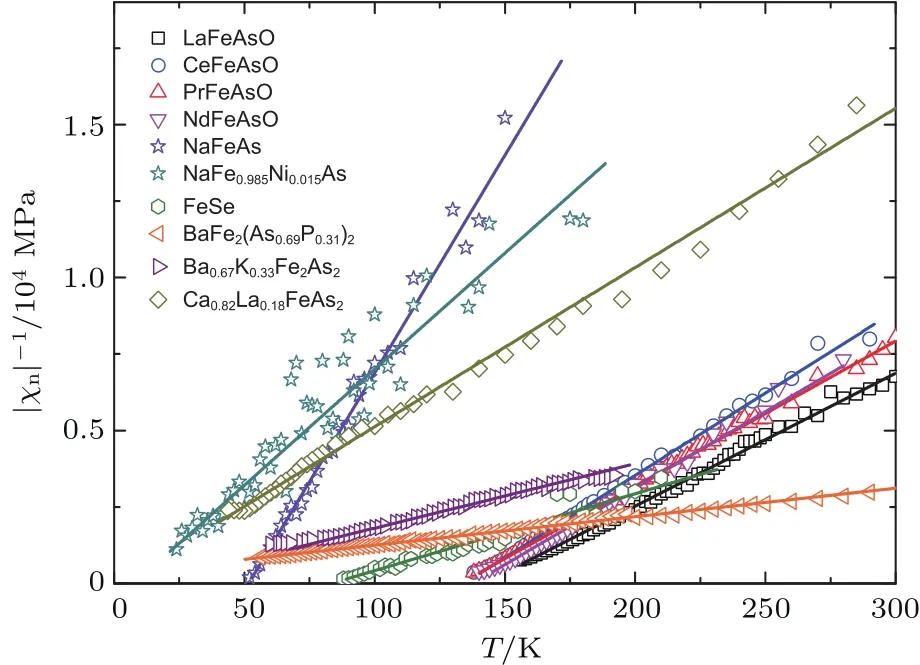
图4 各类铁基超导体中|χn|−1的温度依赖关系[15],其中FeSe,NaFe0.985Ni0.015As,Ba0.67K0.33Fe2As2和Ca0.82La0.18FeAs2中的χn是负的,实线是线性拟合的结果Fig.4.Temperature dependence of|χn|−1in various iron-based superconductor,where the values of χn in FeSe,NaFe0.985Ni0.015As,Ba0.67K0.33Fe2As2and Ca0.82La0.18FeAs2are negative.The solid lines are the linearly fi tted results[15].

图5(a)的结果表明,有序磁矩M的大小和|An|−1大致是线性关系.这一结果包括了三类主要的铁基超导母体,即“1111”(RFeAsO,其中R=La,Ce,Pr,Nd),“Ba-122”(BaFe2As2)以及“111”(NaFeAs).该结果还包含了BaFe2−xNixAs2体系的数据[28],其行为与前述母体相似.然而按传统的说法,Ni掺杂应当引入电子,其行为不应该与母体相符.Ca0.82La0.18FeAs2(“112”)具有非体超导,其数据仍然落在同一条线上.图5(a)中还包含了四类没有反铁磁序的样品,即最佳掺杂NaFe1.985Ni0.015As,BaFe2(As0.69P0.31)2,Ba0.67K0.33Fe2As2和FeSe,都落在最佳掺杂BaFe2−xNixAs2数据点的右侧.有一个特殊的样品是SrFe2As2,其数据偏离得很远.这很可能来源于该体系的反铁磁序是很强的一级相变,因此其反铁磁序的大小在转变附近急剧上升,从而导致与图5(a)中线性关系的偏离.

在磁系统中,磁化率的居里-外斯温度依赖关系中的居里常数对应着磁涨落的强度.类似地,我们工作中向列居里常数|An|对应着向列涨落的强度,来源于局域有效向列序的涨落.因此,图5(a)将高温的向列涨落与零温基态的反铁磁关联起来.这是一个完全意想不到的结果,因为即便是一个纯粹的磁系统,其高温磁涨落与零温基态也没有必然的联系.理论上,为了理解铁基超导体母体中有序磁矩的大小,必须在系统中引入某种阻挫,例如时间涨落和嵌套效应[31,32].我们的结果显示,相同的机制也增强了向列涨落,因此对这些阻挫的微观机理给出了很强的限制.不精确地说,很强的向列涨落代表局域向列序的方向或者强度在时间上很快地涨落,从而导致与其线性关联的反铁磁有序磁矩的降低.也就是说,较强的向列涨落可以阻挫磁系统,从而抑制其反铁磁长程序.

图5(a)的结果对掺杂的机理也有一定的启示.我们从所谓电子型掺杂BaFe2−xNixAs2的结果说起.在BaFe2As2中掺杂5%的Ni可以抑制长程反铁磁序并达到最佳掺杂[33].这一过程通常被理解为Ni掺杂引入了电子载流子.而图5(a)告诉我们,也可以通过另一图像进行理解,即Ni掺杂增强了向列涨落,从而导致反铁磁被抑制及超导出现.这两种解释在BaFe2−xNixAs2中是无法区分的,但是当我们考虑其他体系时,后者就显得更为合理.例如,RFeAsO和NaFeAs这些所谓母体的磁基态可以简单地通过调节|An|−1的强度来获得.所有图5(a)中最佳掺杂的材料,包括空穴掺杂和等价掺杂,同样可以被认为是通过调节|An|−1来获得的.有意思的是,依据图5(a),FeSe本来就应该没有磁有序且超导,因为其|An|−1很小.

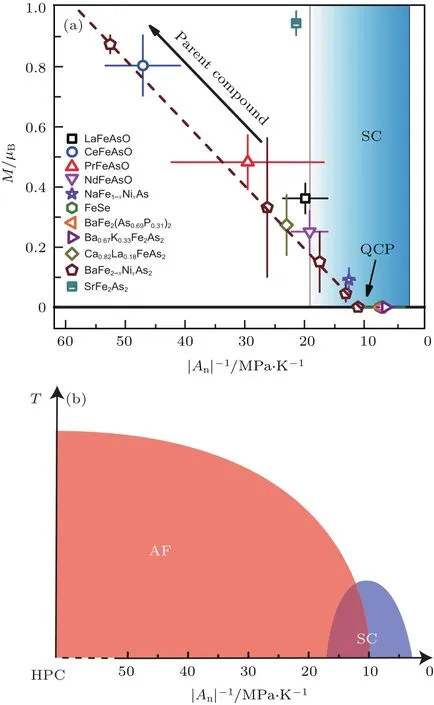
图5 (a)有序磁矩M和|An|−1之间的标度关系[15],直虚线是根据BaFe2−xNixAs2数据[14]而绘制的示意线,有序磁矩的大小和误差来源于之前的中子衍射数据[28],垂直的误差棒来源于多次测量的标准偏差,BaFe2(As0.69P0.31)2,Ba0.67K0.33Fe2As2,FeSe和NaFe1.985Ni0.015As的数据重叠在一起;(b)铁基超导体相图示意图[15],其中超导电性是通过调节|An|−1来抑制一个假设的母体中的反铁磁序而获得的Fig.5.(a)The scaling relationship between the ordered moment M and|An|−1[15].The dashed straight line is based on the data of BaFe2−xNixAs2[14].The values and error bars of the ordered moment are from previous neutron di ff raction results[28]. The vertical error bars come from the standard deviations in multiple measurements.The data points of BaFe2(As0.69P0.31)2,Ba0.67K0.33Fe2As2,FeSe andNaFe1.985Ni0.015As are overlapped with each other.(b)Schematic phase diagram of iron-based superconductors[15],where superconductivity is achieved by tuning|An|−1to suppress the antiferromagnetic order in a hypothesis parent compound.

上述讨论促使我们提出一个统一的铁基超导相图,如图5(b)所示.和传统的相图相比,调节参量不再是载流子而是|An|−1.在该相图中有三个主要方面.首先,存在着一个假设的母体(HPC),具有较大的反铁磁有序磁矩以及较弱的向列涨落.非掺杂的各类铁基材料的基态当然是由其电子结构所决定的,但是等效而言,我们可以将其磁基态理解为通过调节|An|−1而从同一个HPC得来的.从这个角度而言,这些所谓铁基超导体的母体在严格意义上都不是真正的母体.该相图的第二个方面是各体系可能存在着一个向列QCP.由于该QCP在很多体系中发生在最佳掺杂样品中[24],看起来超导的出现也是和|An|−1的减小联系起来的,这也是该相图的第三个方面.这解释了为什么NaFeAs作为母体却可以很容易被掺杂为超导.同时,我们也无需区分电子、空穴和等价掺杂,因为超导在|An|−1足够小时就会出现.这也可以解释为什么FeSe是超导的,因为其|An|−1与其他体系中最佳掺杂样品的值是相近的.

5 结 论

本文综述了我们最近在铁基超导体中通过单轴压强研究向列相的两个主要结果.首先,通过系统地研究BaFe2−xNixAs2中的向列极化率,发现了以下几个符合该系统可能存在一个向列QCP的特征:平均场向列转变温度T′随着掺杂在浓度为0.11处过零;在过掺杂区域向列极化率存在着鼓包行为,其掺杂依赖关系符合量子临界涨落到无序区的过渡;在(100)方向的向列极化率在掺杂浓度为0.11处最强;零温的向列极化率在x=0.11处表现出发散行为.将这一手段扩展到其他铁基超导体系统,发现有序磁矩和向列居里常数存在着简单的线性关系,表明反铁磁序的抑制是通过增强向列涨落来实现的.据此,提出了铁基超导体的统一相图,认为超导电性在向列涨落足够强时才会出现.值得指出的是,这一相图的普适性还需要进一步检验.例如,在H掺杂的“1111”体系中和FeSe在高压下都出现了第二个超导区[34,35],向列涨落是否在该区域仍然起作用值得探索.另外,在Mn,Cr和Cu掺杂体系并未发现超导电性[36],其原因是否与向列涨落有关也仍然不清楚.

感谢文献[14,15]工作中其他作者的贡献.

[1]Keimer B,Kivelson S A,Norman M R,Uchida S,Zaanen J 2015 Nature 518 179

[2]Paglione J,Greene R L 2010 Nat.Phys.6 645

[3]Stephen M J,Straley J P 1974 Rev.Mod.Phys.46 617

[4]Kivelson S A,Fradkin E,Emery V J 1998 Nature 393 550

[5]Oganesyan V,Kivelson S A,Fradkin E 2001 Phys.Rev.B 64 195109

[6]Ando Y,Segawa K,Komiya S,Lavrov A N 2002 Phys.Rev.Lett.88 137005

[7]Daou R,Chang J,LeBoeuf D,Cyr-Choinière O,Laliberté F,Doiron-Leyraud N,Ramshaw B J,Liang R,Bonn D A,Hardy W N,Taillefer L 2010 Nature 463 519

[8]Hinkov V,Haug D,Fauqué B,Bourges P,Sidis Y,Ivanov A,Bernhard C,Lin C T,Keimer B 2008 Science 319 597

[9]Lawler M J,Fujita K,Lee J,Schmidt A R,Kohsaka Y,Kim C K,Eisaki H,Uchida S,Davis J C,Sethna J P,Kim E A 2010 Nature 466 347

[10]Fernandes R M,Chubukov A V,Schmalian J 2014 Nat.Phys.10 97

[11]Chu J H,Analytis J G,de Greve K,McMahon P L,Islam Z,Yamamoto Y,Fisher I R 2010 Science 329 824

[12]Lu X,Park J T,Zhang R,Luo H,Nevidomskyy A H,Si Q,Dai P 2014 Science 345 657

[13]Yi M,Lu D,Chu J H,Analytis J G,Sorini A P,Kemper A F,Moritz B,Mo S K,Moore R G,Hashimoto M,Lee W S,Hussain Z,Devereaux T P,Fisher I R,Shen Z X 2011 Proc.Natl.Acad.Sci.USA 108 6878

[14]Liu Z,Gu Y,Zhang W,Gong D,Zhang W,Xie T,Lu X,Ma X,Zhang X,Zhang R,Zhu J,Ren C,Shan L,Qiu X,Dai P,Yang Y,Luo H,Li S 2016 Phys.Rev.Lett.117 157002

[15]Gu Y,Liu Z,Xie T,Zhang W,Gong D,Hu D,Ma X,Li C,Zhao L,Lin L,Xu Z,Tan G,Chen G,Meng Z Y,Yang Y,Luo H,Li S 2017 Phys.Rev.Lett.119 157001

[16]Chu J H,Kuo H H,Analytis J G,Fisher I R 2012 Science 337 710

[17]Lederer S,Schattner Y,Berg E,Kivelson S A 2015 Phys.Rev.Lett.114 097001

[18]Metlitski M A,Mross D F,Sachdev S,Senthil T 2015 Phys.Rev.B 91 115111

[19]Lederer S,Schattner Y,Berg E,Kivelson S A 2017 Proc.Natl.Acad.Sci.USA 114 4905

[20]Hosoi S,Matsuura K,Ishida K,Wang H,Mizukami Y,Watashige T,Shibauchi T 2016 Proc.Natl.Acad.Sci.USA 113 8139

[21]Böhmer A E,Burger P,Hardy F,Wolf T,Schweiss P,Fromknecht R,Meingast C 2014 Phys.Rev.Lett.112 047001

[22]Gallais Y,Fernandes R M,Paul I,Chauviere L,Yang Y X,Méasson M A,Forget A 2013 Phys.Rev.Lett.111 267001

[23]Thorsm lle V K,Khodas M,Yin Z P,Zhang C,Carr S V,Dai P,Blumberg G 2016 Phys.Rev.B 93 054515

[24]Kuo H H,Chu J H,Palmstrom J C,Kivelson S A,Fisher I R 2016 Science 352 958

[25]Löhneysen H,Rosch A,Vojta M,Wöl fl e P 2007 Rev.Mod.Phys.79 1015

[26]Schattner Y,Lederer S,Kivelson S A,Berg E 2016 Phys.Rev.X 6 031028

[27]Coldea R,Tennant D A,Wheeler E M,Wawrzynska E,Prabhakaran D,Telling M,Kiefer K 2010 Science 327 177

[28]Dai P 2015 Rev.Mod.Phys.87 855

[29]Kasahara S,Shibauchi T,Hashimoto K,Ikada K,Tonegawa S,Okazaki R,Terashima T 2010 Phys.Rev.B 81 184519

[30]Fernandes R M,Abrahams E,Schmalian J 2011 Phys.Rev.Lett.107 217002

[31]Yin Z P,Haule K,Kotliar G 2011 Nat.Mater.10 932

[32]Tam Y T,Yao D X,Ku W 2015 Phys.Rev.Lett.115 117001

[33]Luo H,Zhang R,Laver M,Yamani Z,Wang M,Lu X,Lynn J W 2012 Phys.Rev.Lett.108 247002

[34]Hosono H,Kuroki K 2015 Physica C 514 399

[35]Sun J P,Matsuura K,Ye G Z,Mizukami Y,Shimozawa M,Matsubayashi K,Yan Q 2016 Nat.Commun.7 12146

[36]Ni N,Thaler A,Yan J Q,Kracher A,Colombier E,Bud’Ko S L,Hannahs S T 2010 Phys.Rev.B 82 024519