复杂地质环境下井眼轨迹控制系统研究与设计∗

蔡 振

1 引言

在自动化钻进过程中，解决复杂地质环境下的钻进轨迹控制和钻进安全性是关键工程技术问题［1］。油气钻井工程所遇地层相对单一，多为第四系、第三纪沉积岩，多为大口径、无岩心或部分取心钻进［2］。而地质勘探钻进所遇地层类型多，相对钻进口径小，一般需要全孔取芯［3］。这使得地质勘探钻进过程遇到地层层位多，压力体系复杂，具有高地应力、高地温、高陡构造以及开采扰动的复杂地质力学环境［4］，导致钻进过程强干扰、非线性、强耦合问题突出，给井眼轨迹控制带来很大的困难。

在石油行业中旋转导向钻井技术是现代导向钻井工程的研究重点和发展方向［5］，旋转导向轨迹控制可以实现井下闭环控制。而在地质勘探中井眼轨迹控制系统基本上都是开环系统或是人工地面闭环系统，并不是严格意义上的闭环控制，井下仪器检测的参数需传输至地面，工程技术人员根据各种检测数据和给定的井眼轨迹参数，进而做出下一步决策。石油系统的控制思想可以引入到地质勘探井眼轨迹控制系统中，改进和提升地质勘探轨迹控制效果。

不同地层对钻头的地层阻力也不同，将会导致转向力和控制力之间的对应关系具有不确定性，对井眼轨迹的控制造成影响。同时，井下轨迹控制实施工具，内部机械结构的可靠性、液压系统输出压力的稳定性以及稳定平台内部控制算法的有效性均对轨迹控制精度有影响。上述因素的影响将使井眼轨迹在复杂地质环境下难以有效地控制，因此，本文设计了复杂地质环境下的井眼轨迹控制系统，并使用基于矢量夹角的模糊控制方法来提高轨迹跟踪控制的精度。

2 轨迹控制分析

2.1 控制原理

在地质钻探中，由于地层复杂等原因，实际轨迹往往偏离设计的轨迹。这种偏离，既有方向又有距离，称为偏差矢量［6］。通过计算实际轨迹与设计轨迹之间的偏差矢量，同时考虑轨迹控制要求的造斜率等因素，对轨迹控制系统做出控制指令（即控制钻头的导向力大小和方向），使实际轨迹与设计轨迹尽量接近或重合。

图1 轨迹控制原理图

在轨迹控制过程中存在工程允许偏差即轨迹控制的允许圆柱半径［7］，当偏差矢量的幅值小于控制圆柱半径时，按照设计轨迹的趋势给出控制指令；当偏差矢量的幅值大于控制圆柱半径但小于工具的最大纠错能力时，根据偏差矢量做出合适的控制指令，使实际轨迹尽量靠近设计轨迹。1）钻头起始位置设在a点，在t0时刻偏差矢量为-ab，其模＜εmax（即εmax为有效控制偏差），根据偏差矢量相关计算参数给出控制指令，使实际轨迹逐渐偏向设计轨迹；如果其模＞εmax，超出了工具的最大纠错能力，需要采取强制措施，即更换钻具组合，增大纠偏能力。2）钻头位置在c点时矢量偏差的模＜εmin（即εmin为工程允许偏差），可以认为实际轨迹和设计轨迹接近，按设计轨迹给出控制指令，如图1所示。

2.2 轨迹位置计算分析

井眼轨迹坐标系为O-XYZ，假设α为偏差角、φ为方位角、L为测量深度，kα为倾角变化率，kφ为方位角变化率，其变化率也必须保持在一定的范围内，井斜角偏差变化率Δkα和方位角变化率Δkφ，Δkα≤ε2；Δkφ≤ε3，其中，ε2和 ε3表示允许的最大偏差变化率。假设实际轨迹a点位置参数为a(La，Xa，Ya，Za)，方向参数为 ( )αa，φa，过a点的法平面称为偏差平面［6］。

图2 轨迹控制位置

b点位置参数为 b(Lb，Xb，Yb，Zb)，方向参数(αb，φb)，偏差矢量的偏差距离为

然而在轨迹控制过程中存在滞后性，为避免井眼轨迹波动或超调，实际轨迹的目标点不应该是b点，而是c点，c点位置参数为 c(Lc，Xc，Yc，Zc)，方向参数( )αc，φc，ac在偏差平面上的投影为ac1，ta为a点的切线，实际所求的偏差矢量应为ac1，其偏差距离为

在钻头上施加一个控制力F，减少偏差距离，需要建立起F与 ||ac1之间的函数关系，即F=f（ ||ac1），在控制过程中，影响到偏差距离的因素主要是控制力的幅度和方向。在轨迹控制过程中，当偏差矢量确定，其轨迹逼近的方向就确定，关键就是如何建立控制力F与偏差矢量之间的数学关系，但井下环境的复杂性和不确定性使得井眼曲率和三维控制力振幅之间数学关系复杂难建。

2.3 矢量夹角分析

根据轨迹控制原理，偏差矢量ab的偏差距离不能超过一定的常数，即 ||ab＜ξmax（ξmax代表着有效地控制范围，实际偏差值不能超过有效值，否则，转向工具无法将钻具拉至设计的轨迹），如图3所示。

图3 矢量夹角示意图

实际轨迹和设计轨迹的两个单位长度切向矢量ta和tb之间角度，我们称为矢量夹角θ，参见图3所示。矢量夹角θ越大，说明实际轨迹和设计轨迹偏离越大。偏差矢量的幅度小，矢量夹角θ也可能较大，因此，需要以矢量夹角为控制对象，对矢量夹角θ进行控制，提高实际轨迹和设计轨迹的重合度。过a点做切线，a点单位切线矢量可表示为

过b点做切线，b点单位切线矢量可表示为

两单位切线延长线形成的夹角，为矢量夹角θ，根据矢量的数量积公式有

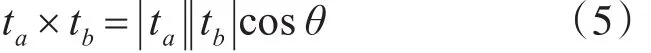
可知，矢量夹角θ为

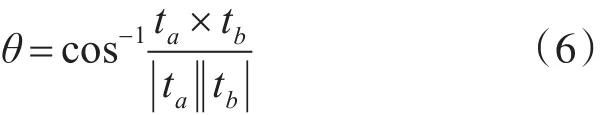
由上式可知，矢量夹角和矢量偏差没有直接关系，但与切线矢量相关（即矢量变化率）。在偏差矢量校正过程中，如果矢量夹角正向增加，说明校正的力度还不够，需要加强转向控制力；如果矢量夹角负向增加，说明校正的力度太大，需要减弱转向控制力。如果矢量夹角减少或保持，则保持转向控制力。因此，通过矢量夹角的变化来反应轨迹偏移程度，相比于偏差矢量几何描述要简单很多，这为轨迹控制系统的控制器设计提供了新的思路和方向。

3 轨迹控制系统设计与分析

3.1 轨迹控制系统结构描述

在地质勘探中，考虑岩层分析，钻探取芯等情况，目前的井眼轨迹控制系统大部分都是直接控制BHA（底部钻具组合），轨迹跟踪控制效果不太理想。为了加强跟踪效果，在BHA的基础上增设反馈环节，从而实现对井眼轨迹的自动控制，井眼轨迹控制系统的结构框图如图4所示。

图4 轨迹控制系统基本结构框图

反馈信号的测量与传输主要由MWD（随钻测量）系统完成，而MWD系统利用泥浆压力脉冲信号完成与地面的信息传输［8］。为了提高井眼轨道的控制能力和实时性，可考虑增设井下闭环控制回路，对现有MWD进行改造，增设传感器和控制器，实现井下闭环控制，本文主要讨论控制器和被控对象，对MWD不展开讨论。

3.2 结构模型

3.2.1 工作原理

整个控制系统的执行结构是可调BHA，即被控对象。可调BHA按工作原理分为可控结构弯角类和可控稳定器类，可控稳定器类包括动力钻具和可控稳定器［9］。本文主要以可控稳定器为对象，主要部件是由上涡轮发电机、下涡轮发电机、电子控制仓及上盘阀、下盘阀组成。稳定器除了受到上、下涡轮电机电磁相反扭矩以外，还受到轴承对平台的摩擦扭矩、钻井液传递给平台的粘滞摩擦扭矩及盘阀系统传递给平台的摩擦扭矩等其他扭矩，这些扭矩均可作为干扰扭矩［10］。

系统的控制对象可认为一个沿自身中心轴自由旋转的刚体［10］。轨迹跟踪控制的目的是通过控制钻头的导向力的大小和方向，实现对井眼轨迹的控制。因此，可通过调整下涡轮电机的控制力矩，平衡上涡轮电机的电磁转矩和干扰扭矩，使被控刚体的空间角稳定在给定值，并且在稳定的同时能够围绕给定值允许有一定程度的偏移。

3.2.2 建立数学模型

井眼轨迹控制过程实际上是一个复杂的系统控制问题，受到许多不确定因素的影响［11］。因此，在建立控制模型上通常忽略一些难以量化和描述的因素，或是对实际情况做一些假设和简化［12］。对于稳定器，其数学模型在相关扭矩数学基础上简化而来，传递函数近似等效为

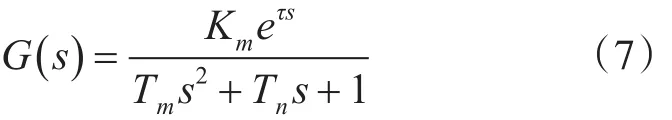
式中，Tm、Tn为时间常数；Km为放大系数；τ为延迟时间常数。

该模型输出量的是角度，事实上描述井眼轨迹控制的表现形式有很多，角度是其中一个比较有用的物理量。在井眼轨迹研究中方位角、工具面角等经常被使用，尤其是工具面角，工具面角是描述钻头钻进趋势的物理量，但这些物理量需要经过专门测量和计算。本文分析了矢量夹角可以很好地描述设计轨迹和实际轨迹之间偏差情况，因此，将矢量夹角作为输入输出量，轨迹控制系统结构模型如图5所示。

图5 轨迹控制系统结构模型

3.3 控制器设计与分析

3.3.1 控制器框图

由于井下具有非线性、时变性等特点［13］，传统的PID控制算法比较受限制，采用模糊控制算法能有效适应系统的不确定性，提高系统的抗干扰性。在文献［14～15］中，对井下系统进行相关模糊控制设计与模拟，表明模糊控制具有一定的优越性，但模型设计过于简单，采用传统的方式，所以，需要更为精细化的设计。

一般的模糊控制都使用误差e和误差导数e˙作为模糊控制的输入量，其本质上相当于一种非线性PD控制，为消除稳态误差，需要加入积分项。本控制器设计中考虑三个输入变量角度误差e，角度误差导数e˙和误差积分∫e d t，其系统结构如图6所示。

图6 模糊控制器结构框图

其中，夹角误差e，误差导数e˙和误差积分∫e d t作为模糊控制器的输入；模糊控制器的输出为

3.3.2 建立模糊规则

井下控制器的信息通过井下传感器的输入信息、随钻测量的数据信息以及地面下传的井眼深度信息来获得［16］，可以从井下反馈的信息可以获得方位角误差Δφ及其变化率误差Δkφ，矢量夹角误差Δθ及其变化率误差Δkθ等。在轨迹控制分析中表明矢量夹角的变化可以基本反映井眼轨迹偏离的情况。因此，将矢量夹角作为模糊控制的输入，通过模糊控制规则来描述输入输出之间的关系。

可取该模糊控制器的输入为矢量夹角误差Δθ及其变化率误差Δkθ，分别记为e和e˙，输出记为u 。 e和 e˙的论域为［-6，6］，有13个整数，将 e和 e˙分为13个等级，同时被模糊化成五级：负大NB、负小NS、零ZR、正小PS和正大PB。模糊控制输出变量u的论域为［-3，3］，分为7个等级，模糊化成五级：负大NB、负小NS、零ZR、正小PS和正大PB。

模糊控制规则的制定需要根据不同的钻具组合、地层数据和岩石特性等因素，同时结合在地质勘探过程中可能遇到的各种情况，最后总结出若干条有效的控制规则，参见表1所示。

从表1可知，当误差e和误差变化率e˙为负大NB时，为了尽快消除轨迹偏差，应当使控制量增大，故使模糊控制的输出量u取正大PB；当e值为正时，可减少控制输出量的变化，使控制输出量u，取零或负；当误差变化率e˙变为正大PB时，控制输出量u不增加。上述模糊规则，就是要尽量减少角度偏差，从而减少设计轨迹和实际轨迹之间的偏差。

表1 模糊规则

4 模糊控制仿真与分析

4.1 模糊控制仿真

假设系统接受步进输入，控制系统检测到输出超过或小于设定值的矢量夹角，然后控制执行结构BHA，使矢量夹角控制在误差范围内，最终稳定输出。通过轨迹跟踪控制，使实钻轨迹按设计路线前行。

在传统工业上使用比较多的控制方法是PID控制方法。在地质勘探中，虽然PID控制方法比较受限制，但在轨迹跟踪控制过程中还是能起到跟踪调节作用。为了实现控制效果对比，结合PID控制方式，系统PID控制方程e d t，经过系统整定，取参数 Kp=5；Kd=0.1；Ki=0.001。在模糊控制中，需要对传递函数G（s）中系数Tm、Tn、Km、τ进行取值，结合钻进过程轨迹控制情况，取参数Tm=1.6；Tn=4.4；Km=15-20；τ=-0.01。输出对比效果如图7所示，虚线表示PID控制情况，黑色实线表示模糊控制效果。轨迹跟踪效果如图8所示。

图7 输出对比图

图8 轨迹跟踪效果图

4.2 仿真分析

从图7输出分析可知，在输入量矢量夹角给定阶跃信号时，PID的反应速度要快一些，快速达到输入值，但PID的超调要大一些，振幅要大一点即输出角度摆幅较大。模糊控制在快速性上表现稍微慢点，但输出稳定性上表现突出，振幅较小。出现这现象的原因，由于地层复杂，PID系数固定，在不同岩石层性能表现相对固定，因此，适应性不太好。

通过图8进行分析，PID在开始轨迹跟踪时出现角度上下摆动比较大，在输出趋于稳定时也没有办法与输入重合，存在小幅偏离情况。模糊控制在开始的摆幅不大，在稳定时基本与输入重合，基本达到了跟踪的效果。由于地质勘探在复杂地质环境下面临岩石层位多样化，对轨迹跟踪要求比较高，因此，采用模糊控制比较合适一些。

综上所述，本文设计的模糊控制系统能够快速地跟踪控制信号，较好地控制超调，能够较好地提高系统的抗干扰能力，能够更好地提高系统的轨迹跟踪能力。

5 结语

1）本文研究的轨迹跟踪控制中引入模糊控制方法，由于井下控制对象的时变性和非线性，使得控制效果相对优于传统PID控制算法，但在模糊规则的制定过程中需要现场经验总结。同时，虽然通过Matlab仿真软件进行验证效果的有效性，但存在一定的局限性，仍需进一步研究实际控制效果。

2）在复杂地质环境下，地质钻进所面对的井下工况复杂，影响钻进轨迹变化的因素很多，并且相关参数不断变化、难以测量。要建立精确的数学模型极为困难，为轨迹跟踪控制系统设计与研究提出了很大的挑战。随着智能控制技术的发展，将智能控制技术应用于地质钻进过程成为提高轨迹跟踪控制精度、增强系统抗干扰能力的技术手段。

3）轨迹控制系统是一个比较复杂的系统工程，其目的是控制导向力使钻头按照预定的轨迹钻进，但该系统在一系列复杂的串级控制过程中，会存在很多耦合作用，参数相互影响，需要研究多参数关联性，建立起交叉学科系统级的控制模型，推动地质钻探智能控制。

［1］Pirovolou D，Chapman CD，Chau M T，et al.Drilling Automation：An Automatic Trajectory Control System［J］.Journal of Petroleum Technology，2011，63（12）：84-87.

［2］Macpherson J D，Wardt J P，Florence F，et al.Drilling-Systems Automation：Current State，Initiatives，and Potential Impact［J］.SPEDrilling&Completion，2013，28（04）：296-308.

［3］Su O.Performance Evaluation of Button Bits in Coal Measure Rocks by Using Multiple Regression Analyses［J］.Rock Mechanics and Rock Engineering，2016，49（2）：541-553.

［4］Kahraman S，Bilgin N，Feridunoglu C.Dominant rock properties affecting the penetration rate of percussive drills［J］.International Journal of Rock Mechanics and Mining Sciences，2003，40（5）：711-723.

［5］张绍槐.现代导向钻井技术的新进展及发展方向［J］.石油学报，2003，24（3）：82-89.

ZHANG SH.New progress and development direction of modern steering drilling technique［J］.Acta Petrolei Sinica，2003，24（3）：82-85.

［6］Di Q F.Studies of rotary steering drilling system for hole trajectory control［J］.Petroleum Drilling Techniques，1998，26（3）：52-54.

［7］李琪，杜春文，张绍槐.旋转导向钻井轨迹控制理论及应用技术研究［J］.石油学报，2005，26（4）：97-101.

Li Q，Du CW，Zhang S.Well trajectory control theory for rotary steering drilling system and applied techniques［J］.Acta Petrolei Sinica，2005，26（4）：97-101.

［8］ Chao D，Zhuang Y，El-Sheimy N.An Innovative MEMS-Based MWD Method for Directional Drilling［C］//SPE/CSUR Unconventional Resources Conference.Society of Petroleum Engineers，2015：134-140.

［9］Zhu，X.，Jia，Y.Y.，&Tong，H..A New BHA's Thoeretical Analysis and Its Successful Applications［C］//CPS/SPE International Oil&Gas Conference and Exhibition，2010：685-691.

［10］Xue QL，Han L J，Yang JZ.Study on control-ling simulation system for stabilizing platform in rotary steer-ing drilling system ［J］.Petroleum Drilling Techniques，2010，38（4）：10-14.

［11］Su Y N.Petroleum Engineering Basic Problems on Design of Automatic Control System of Bit Trajectory［J］.Acta Petrolei Sinica，1999，20（1）：67-72.

［12］Inyang I J，Whidborne JF，Bayliss M T.Bilinear modelling and bilinear PIcontrol of directional drilling［C］//International Conference on Control，2016：1-6.

［13］Panchal N，Bayliss M T，Whidborne J F.Attitude control system for directional drilling bottom hole assemblies［J］.Iet Control Theory&Applications，2012，6（7）：884-892.

［14］Haber R E，del Toro R M，Gajate A.Optimal fuzzy control system using the cross-entropy method.A case study of a drilling process［J］.Information Sciences，2010，180（14）：2777-2792.

［15］Haber R E，Haber-Haber R，Jiménez A，et al.An optimal fuzzy control system in a network environment based on simulated annealing.An application to a drilling process［J］.Applied Soft Computing，2009，9（3）：889-895.

［16］Xiru H，Gonghui L，Jingwei L，et al.Fuzzy control simulation of wellbore trajectory based on matlab/simulink fuzzy tool box［J］.Acta petrolei sinica，2006，27（3）：108.