带杂交算子的自适应混合花粉授粉算法∗
汪 海 赵齐辉 刘 升
1 引言
2012年,著名学者Yang提出了植物花授粉算法[1](Flower Pollination Algorithm),与其前些年提出来的萤火虫算法(FA)、布谷鸟算法(CS)、蝙蝠算法(BA)同样是受到自然现象启发而得出灵感。
FPA算法由于通用性强、鲁棒性好、编程简易,具有较好的稳定性,已成功应用于许多实际中的工程优化问题比如:RGB图像压缩[2],九宫格数独问题求解[3],求解制造单元设计问题[4]。FPA算法如此优秀的应用性能现已成为人工智能一个新的热点。但是FPA也存在易陷入局部最优、理论基础薄弱、收敛性证明缺乏等问题。
针对花授粉算法易陷入局部最优的特点,国内外学者做了很多改进,方法包括:参入局部优化算子和其他算法混合。2015年,Rodrigues[5]提出了一种基于二进制编码的花授粉算法,并应用于特征选择。2014年,El-henawy I,和Ismail M[6]将混沌算法引入到花授粉算法中,并用于整数规划问题的求解。2014年,Abdel-Raouf O[7]将粒子群算法与花授粉相结合,并用于求解约束优化问题。Sakib N[8]等于2014年,将遗传算法引入到花授粉算法之中,运用遗传算法中优胜劣汰的思想进行算法改进。2016年,肖辉辉[9]等将差分进化的机制参入花朵授粉算法之中,并选择典型的标准测试函数进行对比,取得较好的优化效果。
花朵授粉算法结构简单,参数较少,相对已有算法的局部优化和混合其他算法,本文从遗传变异的角度将随机花粉个体与最优个体杂交产生较优的子代;并设计自适应权重使算法具有更合理的开采能力。综上,本文针对花授粉算法的两个关键过程(异花授粉和同花授粉)分别进行改进,对于异花授粉设计一种自适应权重使得权重因子根据迭代次数进行自适应调整;对于同花授粉,引入杂交算子进行花粉个体与最优个体进行杂交使得种群多样性增加,有效地降低陷入寻优的盲目性,最后测试经典函数表明,改进的MFPA在函数优化方面效果优于FPA和DEFPA。
2 基本花授粉算法
萤火虫算法(FA)灵感来自于萤火虫发光吸引异性、布谷鸟算法(CS)来源于布谷鸟的巢寄卵生行为、蝙蝠算法(BA)受启发于蝙蝠的回声定位行为,而花授粉算法(FPA)[1]同样是受到自然界植物花授粉这一行为启发而得出灵感,自然界大约有90%的植物进行生物传粉(Biotic pollination),而存在10%进行非生物传粉(Abiotic pollination),非生物传粉需要通过一些介质进行传播,包括:蜜蜂、蝙蝠、鸟类,而这些动物的传播授粉行为服从莱维分布。
基于植物花授粉的一些特征,在提出该算法之前应当遵循以下理想化规则[1]:
1)进行异花授粉是通过蜜蜂或者鸟类来进行的,而这些异花授粉的“媒介”是进行莱维飞行来传播花粉的,异花授粉我们看出一个全局授粉的过程;
2)自花授粉的过程我们把它看成一个局部授粉的过程;
3)花恒常性可以认为是授粉行为涉及到两朵花的繁殖概率与相似度成比例;
4)全局授粉和局部授粉由转换概率 p∈[0 ,1]控制,受物理位置邻近性的影响以及其他自然因素(风、雨雪等),局部授粉和全局授粉中 p代表着重要的意义。
在FPA算法中,有两个关键的步骤:全局授粉(异花授粉)和局部授粉(自花授粉)。
在全局授粉的过程中,花粉是由“媒介”(例如昆虫)进行飞行而传播,鉴于此,我们把g*定义为当前种群中最优花粉所处的位置,则其位置更新公式如下:

其中:xti+1代表着花粉i在t+1循环时的位置,L代表着授粉的强弱程度,但其本质是一个服从莱维分布的步长因子,服从以下式(2)分布:

其中,Γ(λ)是标准伽马函数,并且这一分布较为合理当 s(s>0)为一个较大值的情况,一般地,取λ=3/2。
当花粉进行自花授粉的过程时,其位置xti更新的公式如下:

和是不同于花粉i的两个花粉的位置,ε∈U[0,1]。
基于以上分析,我们可以将FPA算法步骤描述如下:
1)初始化:给定种群值,自花授粉和异花授粉的转换概率,以及最大迭代次数和ε的值,随机给定一个最优值位置;
2)基于概率 p选择自花授粉和异花授粉:rand<p则进行异花授粉,按照式(1)进行更新新的解;rand>p则进行自花授粉,按照式(3)进行解的更新:f(xnew)<f(g*=xnew);
3)最优值评估:将得出的新解与随机产生的最优花粉进行比较,若 f(xnew)<f(g*),则令g*=xnew;f(xnew)>f(g*),返回2);
4)判断是否达到最大迭代次数;
5)输出最优花粉个体和g*。
3 带杂交算子的自适应花授粉
花授粉算法融入了蝙蝠算法和布谷鸟算法的优点,其在全局授粉的过程引入了莱维飞行,这点跟布谷鸟算法的步长移动服从莱维分布具有相似性;花授粉算法利用转换概率 p来与一个随机数进行比较,然后进行全局授粉和局部授粉过程的切换,蝙蝠算法也将脉冲的响度和发射速率与随机数进行比较,然后进行解的更新。
但是启发于生物现象的算法并不是完全符合自然规律,存在多条假设使得算法会存在一定的缺陷,比如:Yang是根据经验来决定切换概率 p=0.8;考虑到了算法设计的复杂性,假设一朵植物只开一朵花,一朵花的配子代表着一个可行解。这些缺陷使得算法容易陷入局部最优、早熟。
针对花授粉算法的不足,本文在算法的两个过程分别进行改进。在全局授粉的过程之中引入了随机偏好游动的权重,使得算法的寻优过程更为合理;在局部授粉的过程引入遗传算法的杂交思想,将花粉个体进行杂交,这样种群的多样性便可以得到增加。
3.1 动态随机偏好游动
花授粉算法全局授粉过程中的莱维飞行可以使得算法有效地往最优值接近,一定程度上可以跳出局部最优。为避免算法陷入局部最优,本文引入一种动态权重进行随机扰动,公式如下:

其中a代表的是调节因子,其取值依赖实验结果好坏而定,wmax和wmin代表的是最大权重和最小权重,显然wmin≤w≤wmax。
在粒子群算法的研究中,我们可以知道,权重是影响算法性能的一个较为关键的因素。过大的权重容易跳过最优解,局部开采能力不足;过小的权重迭代缓慢,寻优空间较小,全局寻优能力不强。本文提出的是一种递减机制的权重,t→0,w=wmax;反之 t→max t,w=wmin,因此可以很好地协调算法搜索的前期需要较大的寻优空间;后期可以向最优值收敛,加快收敛速度。
3.2 遗传算法的杂交思想
花授粉算法的局部授粉的过程位置更新过程只是随机地借鉴了两个花粉的位置差的信息,这样执行局部授粉搜索最优解的过程具有盲目性和不定向性,对此随机选择一个花粉与上一代的最优个体进行杂交,这样使得其他花粉能够获得最优花粉的信息,并且种群的多样性得到增加。定义如下:
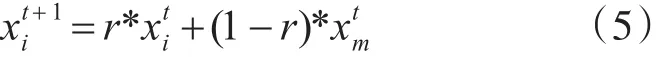
式中r是一个服从0~1之间的均匀分布的随机数,是一个随机产生的花粉个体,经过杂交的操作,位置更新会更加合理,局部搜索的过程方向性更强。
3.3 算法的实施步骤
我们将MFPA的算法流程描述如下:
Step 1:定义目标函数 f(x);x=(x1,x2,…xd)T;
Step 2:花粉种群初始化,随机产生初始最优解;
Step 3:定义转换概率 p;
Step 4:设定迭代终止的条件(一个固定的迭代次数或者需要达到的目标精度);
Step 5:如果 rand<p,权重按照式(4)进行异花授粉;
Step 6:如果rand>p,进行自花授粉,并将种群进行杂交;
Step 7:评价产生的新解,如果优于产生的随机解,则替代掉;否则转到Step 4~Step 6;
Step 8:更新找到的最优解。
4 测试与仿真
由于花授粉算法只涉及一个参数,即转换概率p,Yang在文献[1]中阐明了 p在选取0.8时实验效果较好,FPA算法参数选取转换概率 p=0.8;DEFPA[9]算法参数选取转换概率 p=0.8,CR=0.1,F=0.5;本文算法选取 p=0.8,a=1,wmax=0.96,wmin=0.36,与基本花授粉算法以及基于差分进化策略的花授粉算法[9]进行对比,种群为20,迭代2000次,选取相一致的测试函数,只进行固定迭代次数的寻优的精度对比。
4.1 测试函数
1)min,该函数全局最小值是0。
2)min f2(x)=xi≤10,该函数全局最小值是0。
3)+e,-32.768≤xi≤32.768,该函数全局最小值是0。
4) min f4(x)=-600≤xi≤600,该函数全局最小值是0。
5) min f5(x)=xi≤100,该函数全局最小值是-1。
6)min-5≤xi≤5,该函数全局最小值是0。
4.2 结果分析
f1是单峰函数,全局的最优值并不是十分难以求得,基本FPA算法与最优值相差结果较大,而DEFPA的数量级仅仅停留在10-18,但是MFPA都可以搜索到其最优值,并且寻优标准差达到了0;f2是一个震荡较为强烈的函数,全局最小值不易寻得,MFPA在30次迭代实验中都可以搜寻到最优值并且从图2可以看出来收敛较为迅速;f3是一个指数叠加并且加上余弦函数适当放大的连续型函数,其特点是:曲面起伏不平,很多算法由于在“爬山”搜索的过程中不免落入了局部最小的陷进,但是MFPA要比DEFPA高8个数量级,且寻优结果较为稳定,但也陷入局部最优,这是MFPA需要优化的地方;f4函数的特点是趋于一个单峰函数,MFPA亦可以搜索到最优值0,并且收敛较为迅速;对于二维函数 f5的测试,该函数的最优值被许多局部极小值所包围,FPA和DEFPA的表现差不多,但是MFPA在30次实验过程中均可以收敛到-1;30维的 f6函数,DEFPA可以将精度大提高到了10-3,与0依然存在一定的误差,而MFPA依然找到了算法的最小值。

表1 三种算法测试结果

图1 f1收敛曲线
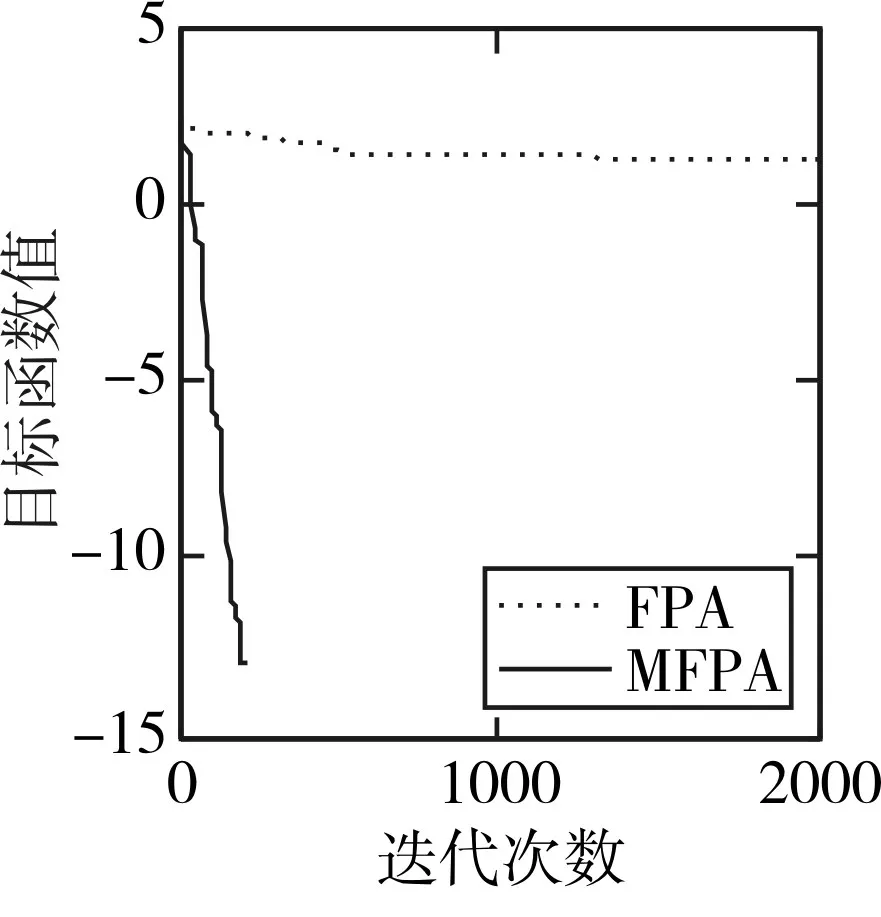
图2 f2收敛曲线

图3 f3收敛曲线
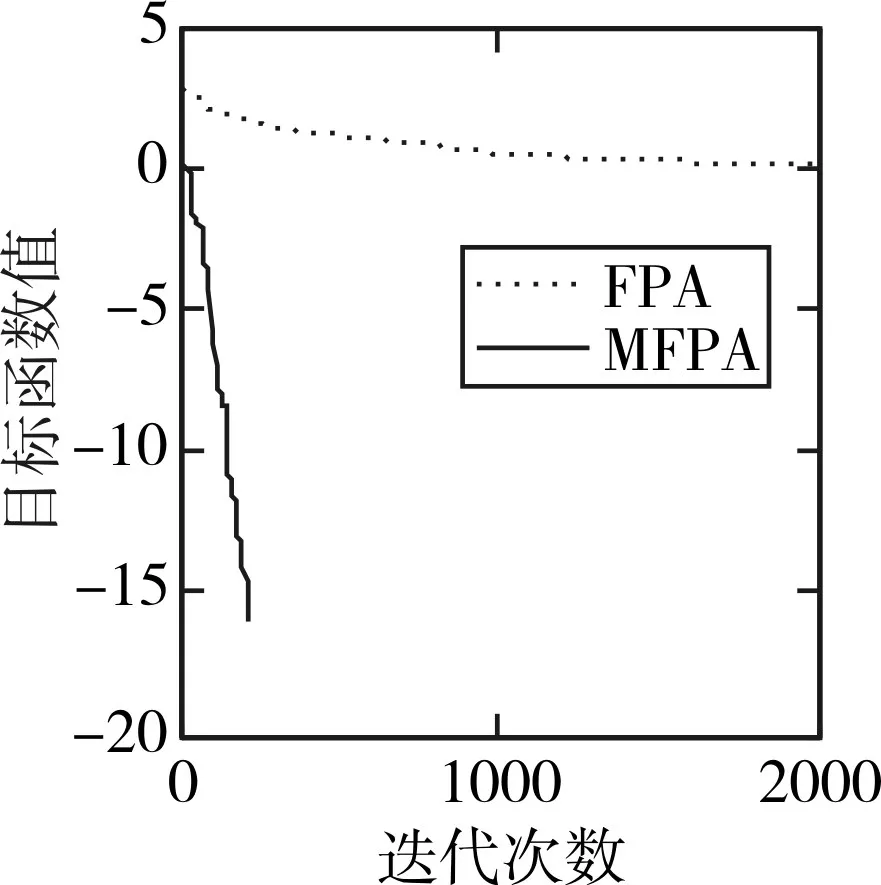
图4 f4收敛曲线

图5 f5收敛曲线
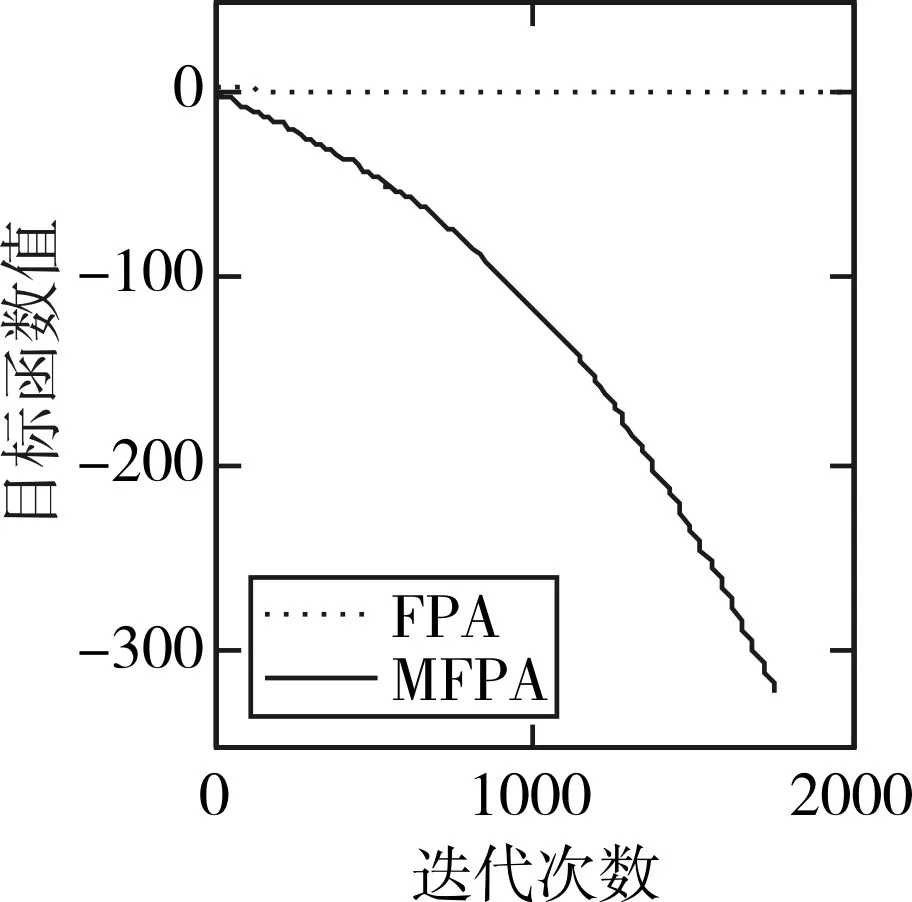
图6 f6收敛曲线
综上所述,除了Ackley函数的求解仅仅是停留在了10-16这一数量级,陷入了局部收敛,其余函数的优化均直接搜索到了其最优值,证明了MFPA的优越性以及有效性,因此说明MFPA在函数优化方面存在一定的优势。
5 结语
本文介绍了一种带杂交算子的自适应花授粉算法,针对花授粉算法中异花授粉和同花授粉进行局部改进。在异花授粉的过程中,对权重进行自适应的设计,使其初期和后期都有良好的寻优表现;在自花授粉过程中,引入杂交算子进行最优个体杂交,以增强种群的多样性,避免陷入局部最优。选取了6个函数进行测试,证明其结果较优,尤其是针对高维多峰函数的优化存在一定的优势。
但是花授粉算法也存在一些不足,比如:收敛性的证明、理论基础薄弱。下一步的工作应该是完善其理论以及证明其收敛性,还包括进一步运用到求解现实中的优化问题。
[1]Yang X S.Flower pollination algorithm for global optimization[M]//Unconventional computation and natural computation.Springer Berlin Heidelberg,2012:240-249.
[2]Kaur G,Singh D,Kaur M.Robust and Efficient‘RGB’based Fractal Image Compression:Flower Pollination based Optimization[J].Proc.of International Journal of Computer Applications,2013,78(10):11-15.
[3]Abdel-Raouf O,El-Henawy I,Abdel-Baset M.A Novel Hybrid Flower Pollination Algorithm with Chaotic Harmony Search for Solving Sudoku Puzzles[J].International Journal of Modern Education and Computer Science(IJMECS),2014,6(3):38.
[4]Soto R.et al.Resolving the Manufacturing Cell Design Problem Using the Flower Pollination Algorithm[C]//In:Sombattheera C.,Stolzenburg F.,Lin F.,Nayak A.(eds)Multi-disciplinary Trends in Artificial Intelligence.MIWAI 2016.Lecture Notes in Computer Science,vol 10053.Springer,Cham,2016.
[5]Rodrigues D,Yang X S,de Souza A N,et al.Binary Flower Pollination Algorithm and Its Application to Feature Selection[M]//Recent Advances in Swarm Intelligence and Evolutionary Computation.Springer International Publishing,2015:85-100.
[6]El-henawy I,Ismail M.An improved chaotic flower pollination algorithm for solving large integer programming problems[J].International Journal of Digital Content Technology and its Applications,2014,8(3):72.
[7]Abdel-Raouf O,Abdel-Baset M.A new hybrid flower pollination algorithm for solving constrained global optimization problems[J].International Journal of Applied Operational Research-An Open Access Journal,2014,4(2):1-13.
[8]Kanagaraj G,Ponnambalam SG,Jawahar N,et al.An effective hybrid cuckoo search and genetic algorithm for constrained engineering design optimization[J].Engineering Optimization,2014,46(10):1331-1351.
[9]肖辉辉,万常选,段艳明.一种改进的新型元启发式花朵授粉算法[J].计算机应用研究,2016,33(1):126-131.
XIAO Huixui,WAN Changxuan,DUAN Yanming.A New Improved Primitive Heuristic Flower Pollination Algorithm[J].Computer Application Research,2016,33(1):126-131.
[10]傅文渊,凌朝东.布朗运动模拟退火算法[J].计算机学报,2014,37(6):1301-1308.
FU Wenyuan,LING Chaodong.Brownian Motion Based Simulated Annealing Algorithm[J].Chinese Journal of Computers,2014,37(6):1301-1308.
[11]Zhang Y,Zhang Y.Particle Swarm Optimization Assisted by Gaussian Processes for Multimodal Function Optimization[C]//International Conference on Computer Engineering and Information Systems,2016.
[12]Kaipa K N,Ghose D.Multimodal Function Optimization[M].Glowworm Swarm Optimization.Springer International Publishing,2017.
[13]Jamil M,Zepernick H J,Yang X S.Multimodal Function Optimization Using an Improved Bat Algorithm in Noise-Free and Noisy Environments[M].Nature-Inspired Computing and Optimization.Springer International Publishing,2017.
[14]Yang X S,Karamanoglu M,He X.Flower pollination algorithm:A novel approach for multiobjective optimization[J].Engineering Optimization,2014,46(9):194-195.
[15]Alma’Shumah F,Permana D,Sidarto K A.Solving inverse problem for Markov chain model of customer lifetime value using flower pollination algorithm[J].Journal of Molecular Structure,2015,1692(1):7-11.

