中国区域专利产出与产业创新效率研究
一 问题提出及文献综述
2015年12月,李克强总理在《政府工作报告》中首次提出要“增加研发投入,提高全要素生产率”。全要素生产率的主要推动力是技术进步和创新。专利作为发明人利用其知识产权获取收益的一种方式,是技术进步和创新的“有形证物”,在新产品研发、生产工艺改进以及产业创新上起重要作用。据统计,2015年中国专利局受理了来自国内外110多万件专利申请,其总量占全世界的40%,超过专利申请大国美日韩的总和,中国已成为世界第一大专利申请国,引发越来越多的学者研究中国专利产出效率问题。
(一)问题提出
创新是一个国家持续发展的动力源泉。21世纪是知识经济的时代,如何通过资源配置将专利产出变现为经济产出,是产业经济发展的关键一环。我国《国家中长期科技发展规划纲要》中提到,到2020年将建成创新型国家;2030年,将建成更加完备的国家创新体系、进入创新型国家前列。
根据《国家创新指数报告2012》,2005-2012年,我国研发投入强度从1.32%上升至1.97%。然而2013年由康奈尔大学和世界知识产权组织(WIPO)共同发布的《全球创新指数》显示,2013年中国的创新指数位列35位,较2012年下降1位。为了弄清中国的专利增长方式是否属于“粗放型”的要素投入模式,需要测度专利的产出效率。
中国的自然地理条件、经济、社会、人口和文化空间等存在显著差异,生产专业化与地域分工使得创新资源的流动和集聚具有明确的区位指向性。沿海省份和工业化较发达的省份,其产出专利的能力较强,但并不意味着它们的专利产出效率高。而欠发达的省份,依然可以通过良好的要素配置和创新资源流动策略,拥有较高的专利产出效率。
“工业4.0”时代已经到来,如何更好地提高产业创新能力是适应我国产业发展新时代的关键。为此,深入研究我国各地区的专利产出效率、效率差异表现、差异背后的成因等,对于认清专利产出效率的区域格局和影响因素、制定相关政策制定具有重要意义。
(二)文献综述
国内外学者对专利产出效率的测量通常采用两种模型:一是非参数的数据包络模型(Data Envelopment Analysis,简称DEA);二是随机前沿的生产函数(Stochastic Frontier Approach,简称SFA)。DEA模型不需要定义生产函数的形式,仅用确定性的生产前沿面来考虑对生产效率的影响,故不能考虑偶然因素产生的随机误差。SFA模型考虑随机冲击的影响,将误差分为随机误差和因非效率因素而产生的系统误差,并运用统计方法来衡量随机冲击对生产效率的影响,从而能够克服这些缺点。
党国英和秦开强(2015)[1]运用SFA模型,分析了2008-2012年中国高新技术产业五大类23个分行业的技术创新效率,结果表明:平均技术创新效率总体稳步升高,不同行业技术创新效率差异明显。而韩兆洲和马佳羽(2016)[2]运用SFA模型和空间计量模型研究了中国“一带一路”省市区域创新效率,发现21世纪海上丝绸之路省市的创新效率较高。白俊红等(2009)[3]则用SFA模型研究了中国区域技术创新效率,结果显示,提高技术创新效率对我国经济增长具有重要意义。韩晶(2010)[4]应用SFA模型研究中国高技术产业创新效率,显示出中国高技术产业整体创新效率呈上升趋势。国外有关R&D投入产出效率的最早研究可追溯到Aigner et al.(1977)[5]和Griliches(1979)[6]的研究,其构建的生产函数框架后来被许多学者引用。如Pakes和Griliches(1984)[7]引用此种分析框架来研究R&D的产出效率问题。之后,Rousseau和Rousseau(1997)[8]、Wang(2007)[9]分别使用DEA模型和三阶段DEA模型来测算R&D的产出效率。随着创新效率的新认识形成,一些学者开始在技术创新效率中加入空间地理因素,如李婧等(2010)[10]利用空间计量分析技术研究1987-2007年中国大陆30个省市创新的空间相关性,结果显示:中国省域之间的创新具有明显的正相关性。史修松等(2009)[11]以省级区域为样本测算空间差异,说明了区域创新效率在时间趋势上呈现阶段性波动,并且论证了区域创新经费的投入较人力资本投入对专利产出效率有更大的促进作用。李正锋等(2015)[12]基于不同区域技术水平的差异,在DEA模型的基础上构建非参数共同前沿,测算中国区域创新效率的技术差异,发现不管是共同前沿还是区域前沿,东部地区的创新效率都远远超过了中部和西部地区。
有关专利产出效率,党国英和秦开强(2015)[1]研究认为,2012年,中国高新技术产业的新产品收入达到25571亿元,为2008年的1.98倍,R&D经费投入达到1733.8101亿元,是2008年的3倍。有学者质疑这个数据的背后是否意味着中国专利产出的快速崛起是依靠低效粗放型的R&D经费投入?中国区域专利产出与产业创新效率之间有何内在联系?提高区域专利产出效率和推动技术进步、生产创新的强大动力源究竟在哪里?现有文献并未就此给出令人满意的答案。本文将以2011-2015年中国区域工业产业专利活动数据为样本,采用SFA模型,扩展研究中国区域专利产出和产业创新效率的影响因素以及内在关联,分析提高区域专利产出效率和推动技术进步、生产创新的强大动力源,绘制全国专利产出地图和区域专利创新地图,以期为科学探讨我国专利产出效率的区域差异和成因以及相关政策制定提供重要参考。
二 中国区域专利产出效率分析
(一)中国区域专利产出效率测度模型
1.模型设定和相关概念
专利是国家按专利法授予申请人在一定时期内对其发明创造成果所享有的独占使用、处分和收益的权利。它包括发明专利、实用新型专利和外观设计专利,专利产出的基本依据是发明创造成果。专利产出模型可采用生产边界生产函数模型。生产边界是指生产函数的可能性边缘,即在一定的生产要素投入和一定的技术水平前提条件下,根据“帕累托最优”基本原理所能达到的最优产出,称为前沿面。现实中由于受到各种不可控制因素的影响,实际产出往往小于前沿面。因此,实际产出与最优产出之间的比值可定义为生产效率。最优产出和实际产出之差与理想产出的比值可定义为非效率。
假设现有n种投入要素(X1,X2,…,Xn),实际产出为Y,生产函数为f(X1,X2, …,Xn),则最优产出为Yf(X1,X2, …,Xn),则生产效率为Y/Y。因此,就有必要估计出在投入要素一定时的最优产出,也就是生产边界。再由实际产出的观察点与生产边界的距离,测算出相应的生产效率。
2.非效率的组成
由于前沿生产函数不能测量经济社会随机因素的影响,Aigner et al.(1977)[5]和Battese(1992)[13]等提出了具有复合扰动项的随机边界模型,即随机扰动项εi,其由两部分组成(u和v),则:
εi=ui+viui<0(i=1, 2, …,n)
(1)
其中:非正的扰动项ui为复合结构,为非效率项,表示企业能够控制的因素对产出的影响。其非正性说明了产出只能也必须处于生产可能性边缘上或在其下,不能超出边界范围。生产单位的实际产出与其前沿面的偏离不完全受控于该生产单位,它还受到随机扰动项vi的影响。所以,vi表示不受决策单位控制的随机因素。
3.专利产出效率模型
传统的经济学理论认为,专利的产出是要素投入产生的结果。因此,设专利的产出为Q,要素投入为X,则有生产函数:Q=f(β,X),其中β为参数。据此,本文建立的专利产出效率估计模型,即SFA模型,形式为:
Qit=f(β,Xit)exp(Vit-Uit)
(2)
其中,i=1, 2, …,n;t=1, 2, …,T。根据中心极限定理,假设vi为均值为0的独立同分布的正态分布,即Vit~iid.N(0,σ2v),表示随机扰动的冲击影响。ui独立于vi,ui分布的实际情况可以这样分析:ui衡量系统非效率的程度,而系统性的非效率处于中间水平较多,极端情况较少。但是,ui是不对称的,坏的效率可能会很低,但好的效率又不能超过生产边界。从而没有理由认为随着非效率程度的增加,企业的数量将会单调递减。据此,可根据概率论与数理统计的相关理论,将ui假定均值为众数(非零)的截尾正态分布,而均值为0只是一个特例。如图1所示。

图1 截尾正态分布图
ui假定服从均值为μ、方差为σ2u、被截去ui<0部分的半正态分布,则ui的概率密度函数为:
f(u)= 1[1-F*(1-μ/σu)]2πσue-1/2( u-μαu )2
(3)
其中F*为标准正态随机变量的分布函数。
假设ui为外部环境因素的函数。所以对于企业来说,这些非效率因素是可以控制的。因此,在产出效率模型中加入可控制的环境因素,则:
μi=δzi
(4)
其中:zi为影响非效率的环境因素,δ为环境因素的系数。
所以,关于专利产出效率的估计,定义模型为:
lnQ=lnf(β,Xi)=β0+∑ni=1βilnXi+vi-ui
(5)
其中:生产效率Ei定义为实际产出期望与前沿面产出期望的比值,即:
Ei=QiQ= exp(lnXiβi-ui)exp(lnXiβi) =exp(-ui)
(6)
可见,专利产出效率与定义的非效率因素具有相反的效果。即非效率因素ui的符号为负,则对专利产出效率有正的影响;反之,则有负的影响。
4.模型估计
SFA模型采用极大似然法进行估计,似然估计的表达式:
lnL=-n2 ln(π/2)-n2 ln(σ2s)+∑ni=1ln[1-φ(zi)]- 12σ2v∑ni=1(lnyi-xiβ)2
(7)
其中:xi=lnXi,lnQ=xiβ+vi-ui;σ2s=σ2v+σ2u,γ=σ2uσ2s;zi= (lnyi-xiβ)σsr1-r;φ(·)是标准正态分布函数。
(二)中国区域专利产出效率测算
运用上述SFA模型对中国2011-2015年各个省份的专利产出效率进行测度。其生产函数模型,参考Griliches(1979)[6]构建的知识生产函数模型,选取经济学上常用的柯布道格拉斯生产函数(以下简称C-D生产函数)f(K,L)=KαL1-α, 0<α<1。产出变量为专利申请数(Q),投入变量主要有两个:R&D经费投入(X1)表示C-D生产函数中的资本投入、R&D人员总数(X2)表示C-D生产函数中的劳动力投入。以下设定两个产出效率的环境因素:
(1)R&D项目数(z1):各省份R&D项目数与专利的产出效率息息相关,从某种程度上来说,应该具有严格的正相关关系,且代表着各个省份的科研实力。
(2)经济水平(z2):一个省份的经济水平可能对整个省份的专利产出效率有正向影响。在这里,本文采用各地区生产总值来衡量一个省份的经济水平。
中国2011-2015年各省、市、自治区专利活动数据来源于《中国统计年鉴》。为了消除价格的影响,以固定资产投资价格指数和工业生产者购进价格指数的平均数对R&D经费投入作平减处理,并对投入和产出数据进行对数变换。
根据以上分析,设定SFA模型为:
lnQ=β0+β1lnX1+β2lnX2+δ0+δ1z1+δ2z2+vi-ui
(8)
运用Frontier Version 4.1对以上数据进行估计,所得结果如表1所示。
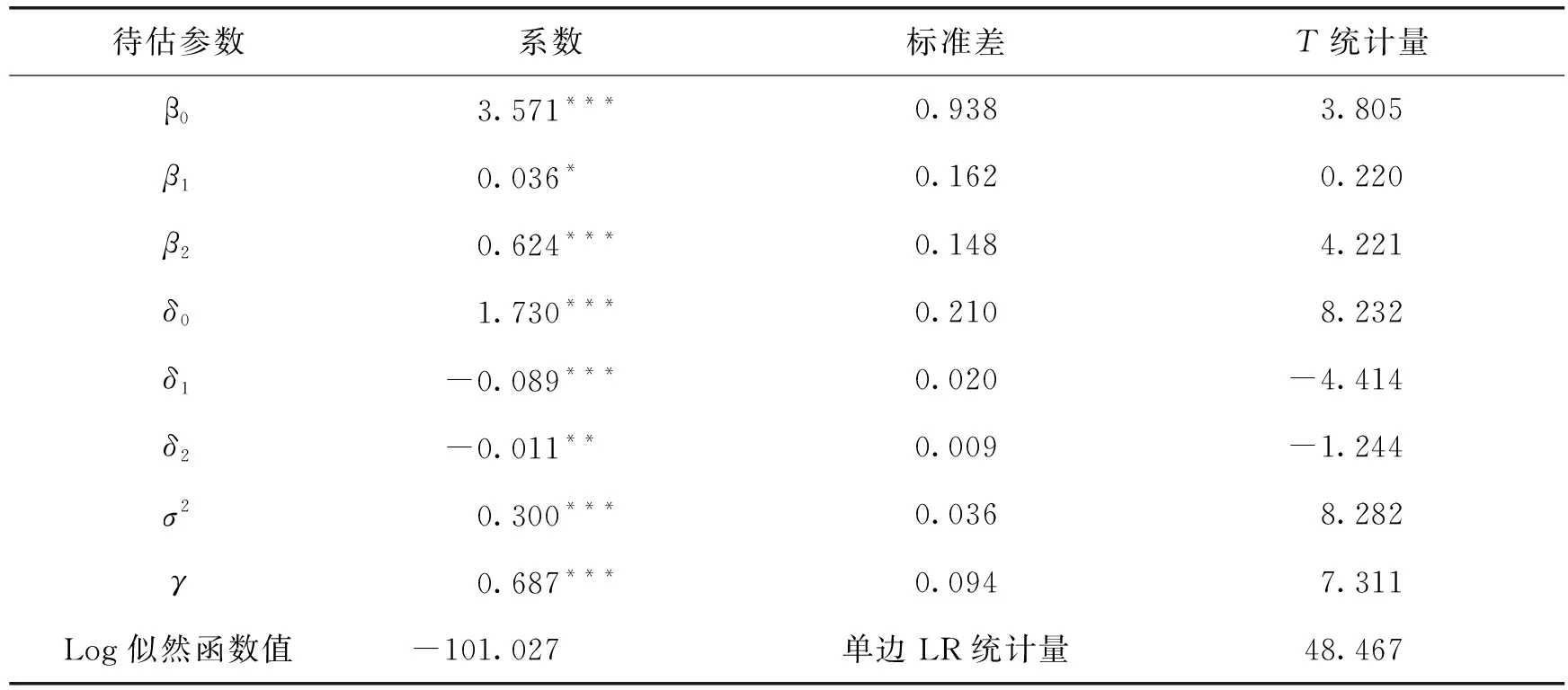
表1 最大似然估计结果
注:*、**、***分别表示通过10%、5%、1%的显著性水平检验。LR为似然比统计量,且它服从混合卡方分布,即χ2分布。在非效率项估计模型中,各参数表示对非效率项影响,负系数表示正向影响。
从表1SFA模型整体估计结果看,γ=0.687,统计显著。说明随机前沿模型误差项中有68.7%来自于技术非效率。LR统计量为48.467,通过了1%的显著性水平检验,说明生产函数中随机误差项具有十分明显的复杂结构,据此采用随机前沿分析技术解释技术差异的方法是合理的。
(三)专利产出效率
1.专利产出弹性
SFA模型中,专利产出的投入变量为R&D经费投入和R&D人员总数。从最大似然估计的结果来看,R&D经费投入增长1%,专利产出会增长0.036%;R&D人员投入增长1%,专利产出增长0.624%,且其系数都通过了t检验。R&D人员投入的产出弹性大于R&D经费投入,说明中国现在的区域专利产出大多属于资本密集型。未来,若要进一步提高专利产出效率,需进一步增加科技研发人员数。同时,R&D经费和R&D人员投入的产出弹性之和为0.660,小于1,说明中国各省份之间的区域创新活动尚不具有规模递增效应。
2.专利产出环境因素
R&D项目数和经济水平的系数为负,说明其对专利产出有正向的影响,两者的系数均通过t检验。但是,从系数的大小来看,R&D项目数较经济水平对专利产出效率有更大的影响。这种结果表明:
(1)各个省份需积极申请R&D项目,促进其区域创新能力。实践证明,R&D投入越多,专利产出越多,科技创新能力越强。积极申请R&D项目,可以在R&D项目的研发中产生更多的专利申请。因为从SFA环境因素的影响效应来看,目前R&D项目对专利产出具有正向作用。即R&D项目较多的省市,其专利产出效率会相应的提高。
(2)各省份经济水平对专利产出效率产生了正面的影响。供给侧结构性改革旨在调整经济结构,使要素实现最优配置,提升经济增长的质量和数量。基于经济水平这个环境要素对于专利产出效率的正向效应,各省要积极推动供给侧结构性改革,提高经济发展水平,为创新活动提供更加良好的制度和资本平台,促进其产出效率的提高。
3.专利产出效率
从SFA模型估计可以得出中国31个省、市、自治区的专利产出效率,如表2所示。

表2 2011-2015年中国各省、市、自治区专利产出效率与排名
(1)2011-2015年中国专利产出区域平均效率。从上述各省、市、自治区专利产出平均效率结果来看,区域之间差异很大(如图2所示)。最近5年,31个省、市、自治区的平均专利产出效率为0.458。专利产出平均效率最高的为江苏(0.948)。据《中国区域创新能力报告》,江苏连续7年位居中国区域创新能力榜首。江苏专利产出效率高和产业创新能力强已成为其发展的鲜明特征和强劲动力。紧随其后的为浙江(0.937)和广东(0.920),这两个省份的经济总量和经济增长速度在全国也是名列前茅。从全国来看,区域的专利产出效率与宏观经济指标高度相关。专利产出效率比较低的地区是海南(0.195)、内蒙古(0.157)、青海(0.147)、宁夏(0.138),这4个地区的专利产出平均效率都低于0.2。
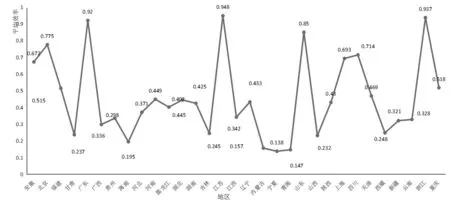
图2 2011-2015年中国各省、市、自治区专利产出的平均效率折线图
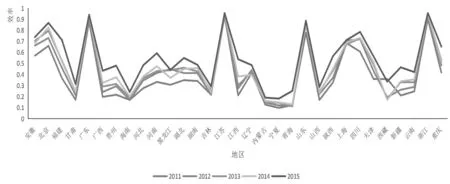
图3 2011-2015年中国各省、市、自治区专利产出效率折线图
进一步分析图3可以看出,各省、市、自治区在2011-2015年的专利产出效率基本稳定。省份有大有小,产值有高有低,基本稳定的总体情况下,各省、市、自治区专利产出效率提高快慢不同。导致平均产出效率差距的原因主要有两点:一是经济发达、交通便利的省份容易形成产业集聚效应,从而提高其产出效率;二是经济欠发达的省份,由于没有总部经济的优势以及配套的创新产业激励政策,导致其专利产出的低效率。因此,在创新方面落后的省份,需要政府配套出台相关创新激励政策。
(2)2011-2015年中国专利产出平均效率变化趋势。从整体平均效率来看(图4),中国专利产出效率逐年递增,从2011年的0.388增长到2015年的0.542,合计增长39.69%。
4.专利产出模型相关说明
专利的产出效率是一个相对概念。例如2015年安徽省的专利产出效率为0.738,表示相对于其他地区效率较高,在本模型系统内处于领先地位。若2015年安徽省的专利投入与产出数量不变,而其他地区的产出有较大提高,则在重新估计模型时,这个产出效率会降低。
最后,测算出2011-2015年全国5年专利产出的平均效率为0.458,把这一平均效率当作中国专利产出效率的及格线,可以清楚地看出各省、市、自治区专利产出效率的相对位置。
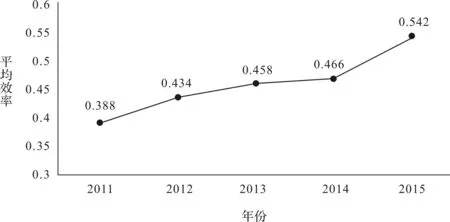
图4 2011-2015年中国区域专利产出的平均效率折线图
三 中国工业专利产出效率分析
本部分拟从工业整体及分行业视角探究专利产出效率的动态演变及行业差异,以进一步厘清我国专利产出效率的变动及差异规律。
(一)中国工业专利产出效率模型和参数估计
运用SFA模型对2011-2015年工业38个行业的创新效率进行测度。产出变量为各行业专利申请数(Q),投入变量主要有两个:(1)各行业R&D经费投入(X1)表示C-D生产函数中的资本投入;(2)各行业R&D人员总数(X2)表示C-D生产函数中的劳动力投入。z1为各行业专利产出效率的环境因素,用各行业R&D项目数衡量。
中国各行业的专利活动数据均来源于《中国统计年鉴》。具体数据的处理方法同前。设定SFA模型为:
lnQ=β0+β1lnX1+β2lnX2+δ0+δ1z1+vt-ut
(9)
运用Frontier Version 4.1对模型进行估计,结果如表3所示。
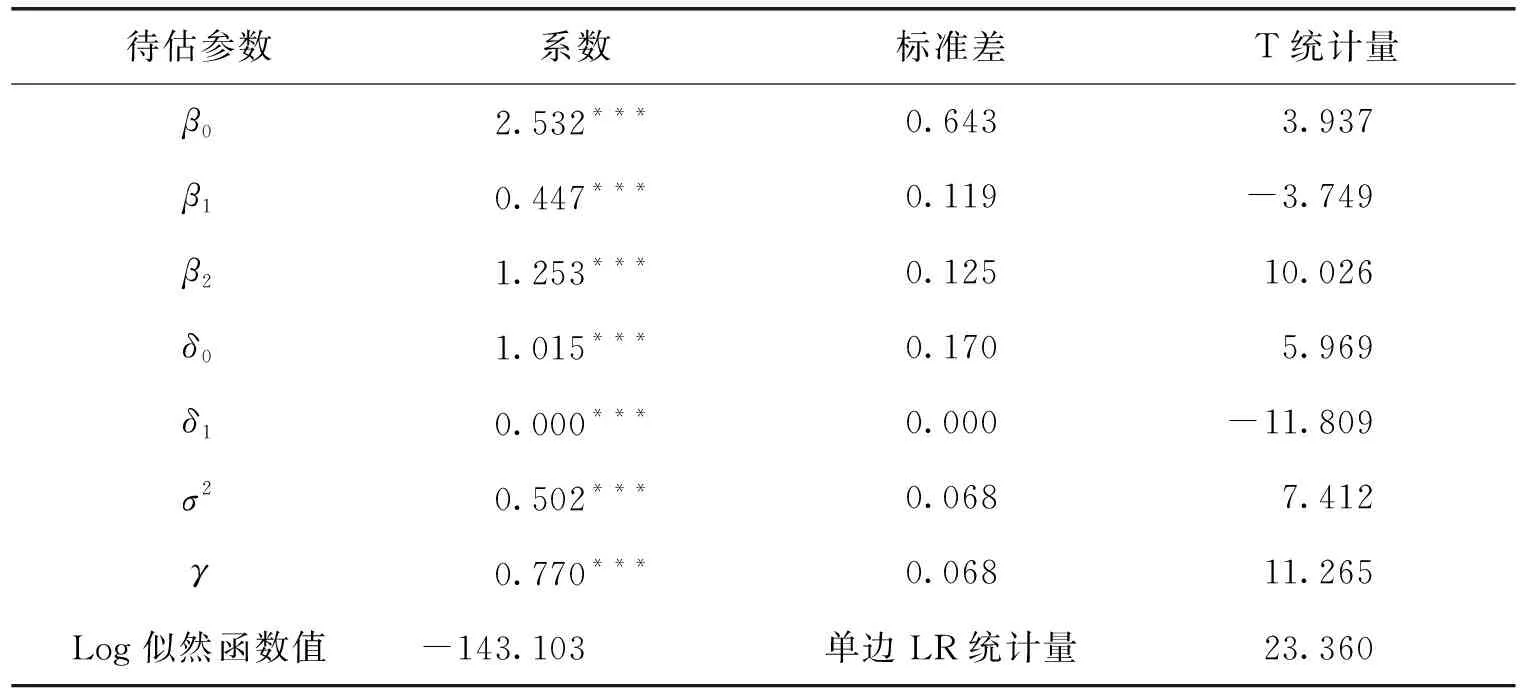
表3 最大似然估计结果
注:δ1的系数并不为0,真实系数为-1.53E-04。
从表3的SFA模型整体估计看,γ=0.770,统计显著,说明随机前沿模型误差项中有77.0%来自于技术非效率。LR统计量为23.36,通过1%的显著性水平检验,说明生产函数中随机误差项具有十分明显的复杂结构,据此采用随机前沿分析技术解释技术差异的方法是合理的。
(二)中国工业专利产出效率
1.工业专利产出弹性分析
SFA模型中,创新投入变量为R&D经费投入和R&D人员总数。从结果来看,R&D经费投入增长1%,专利产出效率将会增长0.447%;R&D人员投入增长1%,专利产出效率将会增长1.253%,且其系数都通过了t检验。R&D人员投入的产出弹性大于R&D经费投入,说明当前我国工业专利产出大多也属于资本密集型,未来想要更好地提高工业专利产出,仍需要大量增加科技研发人员。
2.创新环境因素分析
各行业R&D项目数的系数虽然显著,但是系数值很小。说明R&D项目对专利产出效率没有多大的影响,主要还是各行业投入要素影响产业创新效率。
3.分行业专利产出效率分析
从SFA模型估计可以得出38个行业专利产出效率,如表4所示。
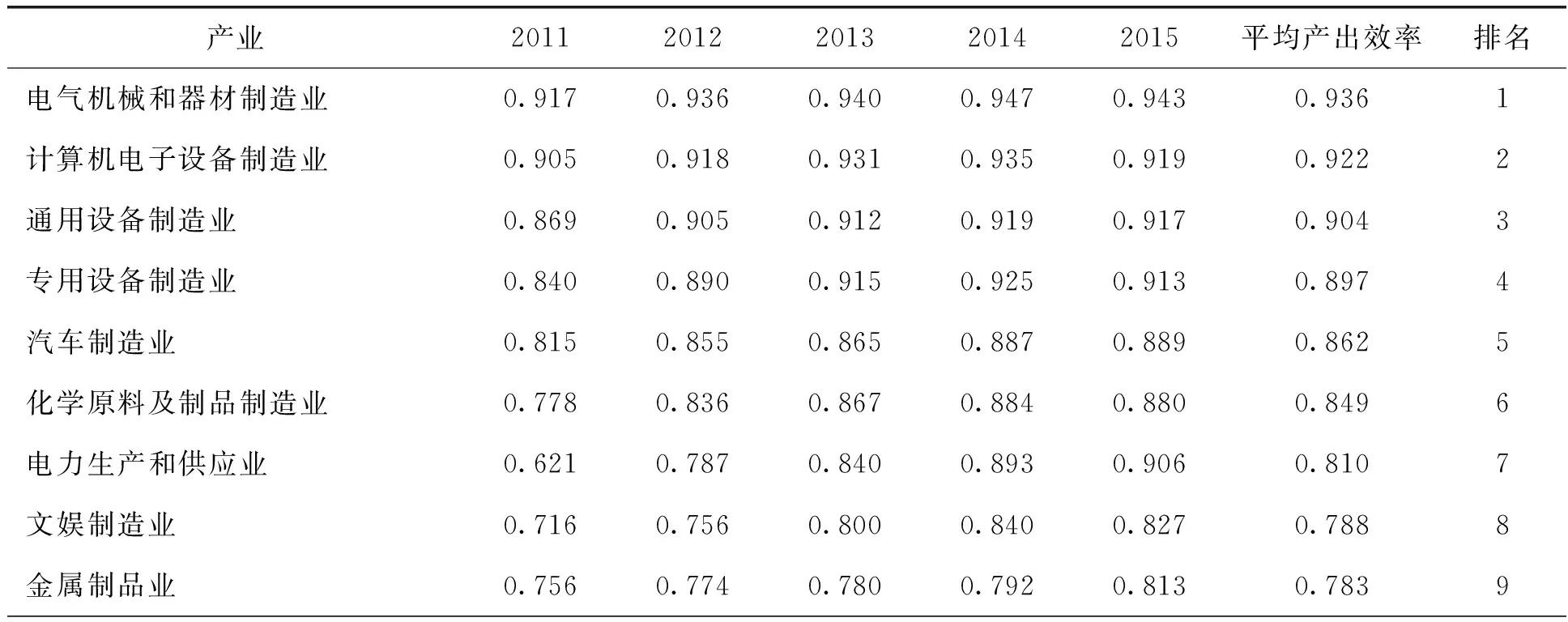
表4 2011-2015年中国工业各行业专利产出效率及排名

(续上表)
注:简明起见,对38个工业行业的名称进行了简化处理。
从各行业平均专利产出效率结果看,行业之间的差距较大。最近5年,38个工业行业的平均专利产出效率为0.602。排名前三的为电气机械和器材制造业(0.936)、计算机电子设备制造业(0.922)以及通用设备制造业(0.904),其每年的产出效率基本都保持在0.9以上。排名比较靠后的是煤炭开采和洗选业(0.223)、非金属矿采选业(0.213)以及有色金属矿采选业(0.206),其每年的产出效率基本都保持在0.2左右。
综上,中国各省、市、自治区工业各行业的整体专利产出效率具有以下几个特征:
(1)工业与区域专利产出效率密切相关,工业专利产出效率高必然推动区域专利产出效率走强。
(2)高科技含量产业创新效率是推动区域专利产出效率的主要动力。如具有高科技含量轻工业领先的省市,其区域专利产出效率较高;而传统的重工业创新效率较低的省市,则区域专利产出效率普遍较低。
(3)传统重工业走出创新效率的低谷,是振兴重工业的必由之路。
四 中国区域专利产出创新地图
区域专利产出效率是区域创新能力的一个重要标志。专利产出效率地图可以展示区域创新效率的差异及创新资源的空间集聚效应和扩散效应。
(一)中国区域专利产出地图
为更为详尽地了解中国区域专利产出的空间差异,本文以2011-2015各省、市、自治区的专利授权平均数为基础,绘制出中国区域专利产出地图,如图5所示。
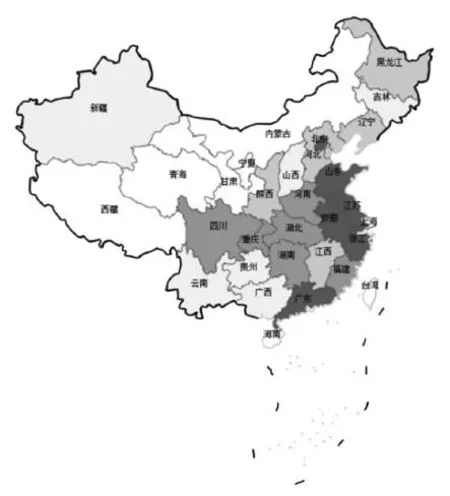
图5 中国部分区域专利产出地图
注:(1)x轴代表经度,y轴代表纬度,颜色越深代表专利产出量越大;(2)按照《中华人民共和国宪法》规定,目前中国有34个省级行政区,即4个直辖市、23个省、5个自治区、2个特别行政区。由于数据不匹配的原因,图5仅为中国部分省市、自治区专利产出地图,不含香港特别行政区、澳门特别行政区和台湾省。
从图5可以看到:(1)中国专利产出量比较大的省份为江苏、浙江、广东,而且沿海省份的地图颜色明显深于内陆省份,说明沿海省份的专利产出量高于内陆省份。(2)专利产出量大,并不一定意味着其专利产出效率高。
(二)中国区域创新效率地图
专利作为区域创新的“实物凭证”,其产出效率在一定程度上反映了区域创新的能力。为全面了解全国整体的专利产出效率和空间结构,本文以2011-2015年各省、市、自治区专利产出的平均效率为基础,绘制了中国区域创新地图。

图6 中国部分区域创新地图
注:(1)x轴代表经度,y轴代表纬度,颜色越深代表区域创新能力越强;(2)按照《中华人民共和国宪法》规定,目前中国有34个省级行政区,即4个直辖市、23个省、5个自治区、2个特别行政区。由于数据不匹配的原因,图6仅为中国部分省市、自治区创新能力地图,不含香港特别行政区、澳门特别行政区和台湾省。
从图6可以看出,(1)中国区域创新活动有明显的空间集聚现象,区域创新效率排名靠前的省份,基本集中于沿海地区,这和专利产出地图的结果基本一致。根据《中国海洋统计年鉴2015》对中国沿海省份*注:根据《中国海洋统计年鉴2015》对沿海省份的划分,中国共有11个沿海省份,从北到南分别是:辽宁、河北、天津、山东、江苏、浙江、上海、福建、广东、广西、海南。的划分,我国11个沿海省份的专利产出效率为0.603,高出平均水平32个百分点。内地省份的专利产出效率为0.378,远低于平均水平。(2)沿海省份也并非都是创新效率比较强的省份,例如海南的专利产出效率仅为0.195。反过来,内陆省份也有创新效率比较强的省份,比如北京、四川、安徽。(3)从专利产出效率的空间结构上看,创新效率靠前的省份集中于东部沿海地区,而排名相对靠后的省份集中于西北地区,也就是工业化开始较晚的省份。这种专利产出效率的空间区域差异是导致区域创新能力差异的主要原因。
五 研究结论与政策建议
(一)研究结论
运用SFA模型测算了2011-2015年中国各省、市、自治区专利产出效率以及工业各行业专利产出效率,结果表明:(1)5年以来,中国区域及各行业专利产出效率保持平稳增长;(2)从专利产出的投入要素和环境因素来看,中国专利产出基本属于高效集约式的增长方式,在工业方面表现尤为突出;从整体上看,否定了中国专利产出的快速崛起是依靠低效粗放型R&D经费投入的观点;(3)从工业专利产出效率与区域专利产出效率的关系来看,两者密切相关,高科技含量产业创新效率是提高区域专利产出效率和推动技术进步、生产创新的强大动力源;(4)从专利产出的空间结构来看,中国区域专利产出效率发展极不平衡。
(二)政策建议
根据中国区域及各行业专利产出效率的变动趋势和差异,本文对进一步提升专利产出及产业创新效率提出如下政策建议:
1.政府和相关法律部门要为区域技术创新和产业创新营造一个良好的法律环境。加快制度创新,释放新的“改革红利”,建设与发展区域产权交易市场,进一步促进产业结构的调整和升级,寻找新的经济增长潜能。
2.政府和相关部委应该更好地为科研单位、工业企业的技术创新提供优质服务。努力降低生产要素的流动成本,保障科研工作的顺利进行。进一步加快落后地区的交通、通讯等基础设施建设,解决落后省份的区域创新“瓶颈”。
3.企业内部需要建立良好的资本和劳动配置策略,加大各大经济圈的人力资本投入力度。对于各省份来说,要加强对高技术人才的吸引力,发挥政策对人才成长的导向作用。使得每一位技术人才有更多的创新激励,进而提高每一个行业、每一个企业的专利产出效率。
4.知识产权局应建立一套合理的专利评估体系。加速专利的成果转化,调动企业和科研院所的创新积极性。各地区政府要加强相关产业创新激励政策,包括财政补贴、税收豁免、税率优惠等措施,激励企业持续不断地开展创新研发活动。
5.各地区之间应该相互借鉴优秀的创新经验。增加圈内省市之间的分工与合作关系,取长补短。进一步发挥经济圈的中心作用,积极发挥中心省市对周边省市和区域的综合影响力及辐射带动作用。实现产业合理布局和错位发展,抓住机遇促进创新产业向中国西北和西南省市转移,使得整个中国的专利活动协调发展。
6.产业之间应当积极寻求产业要素投入与绩效产出之间的动态最优均衡。进一步通过各要素之间的相互作用,产生“1+1>2”的协同效应,提高产业创新的系统绩效。
总之,通过政府和企业共同努力,变现专利要素为经济产出,中国才能成为全球创新能力的翘楚。全面提高专利产出效率和产业创新效率,推动经济增长的质量和效益,中国才能更好地贯彻落实国家创新驱动发展战略。
[参考文献]
[1] 党国英, 秦开强. 高技术产业的技术创新效率与影响因素——对五大类23个分行业的效率分析[J]. 产经评论, 2015, 6(2): 15-27.
[2] 韩兆洲, 马佳羽. 中国“一带一路”省市区域创新效率及空间效应[J]. 产经评论, 2016, 7(2): 110-119.
[3] 白俊红, 江可申, 李婧. 应用随机前沿模型评测中国区域研发创新效率[J]. 管理世界, 2009, (10): 51-61.
[4] 韩晶. 中国高技术产业创新效率研究——基于SFA方法的实证分析[J]. 科学学研究, 2010, 28(3): 467-472.
[5] Aigner, D., Lovell, C., Schmidt, P.. Formulation and Estimation of Stochastic Frontier Production Models[J].JournalofEconometrics, 1977, 6(1): 21-37.
[6] Griliches, Z.. Issues in Assessing the Contribution of R&D to Productivity Growth[J].BellJournalofEconomics, 1979, 10(1): 92-116.
[7] Pakes, A., Griliches, Z.. Patents and R&D at the Firm Level: A First Look[A]// Griliches, Z.(ed.).R&DPatentsandProductivity[M]. Chicago: University of Chicago Press, 1984.
[8] Rousseau, S., Rousseau, R.. Data Envelopment Analysis as a Tool for Constructing Scientometric Indicators[J].Scientometrics, 1997, 40(1): 45-46.
[9] Wang, E. C.. R&D Efficiency and Economic Performance: A Cross-country Analysis Using the Stochastic Frontier Approach[J].JournalofPolicyModeling, 2007, 29(2): 345-360.
[10] 李婧, 谭清美, 白俊红. 中国区域创新生产的空间计量分析——基于静态与动态空间面板模型的实证研究[J]. 管理世界, 2010, (7): 43-55.
[11] 史修松, 赵曙东, 吴福象. 中国区域创新效率及其空间差异研究[J]. 数量经济技术经济研究, 2009, (3): 45-55.
[12] 李正锋, 逯宇铎, 于娇. 基于共同前沿方法的中国区域创新效率及差异研究[J]. 工业技术经济, 2015, (5): 12-19.
[13] Battese, G. E., Coelli, T. J.. Frontier Production Functions, Technical Efficiency and Panel Data: With Application to Paddy Farmers in India[J].JournalofProductivityAnalysis, 1992, 3(1-2): 153-169.

