基于VOF方法的砂土液化后流动变形分析
周恩全, 朱晓冬, 陆建飞, 左 熹, 王炳辉
(1. 江苏大学 土木工程与力学学院, 江苏 镇江 212013; 2. 金陵科技学院 建筑工程学院, 江苏 南京 211169; 3. 江苏科技大学 土木工程与建筑学院, 江苏 镇江 212005)
砂土液化是指在地震作用下,饱和砂性土由于孔隙水压力上升,有效应力减小,从而导致土体强度衰减而呈现液态的现象.1983年日本Nihonkai-Chubu地震中,砂土液化大变形导致不少桥梁及地下结构等构筑物受到破坏[1],由此引起业界学者们对液化砂土侧向变形的关注.近年来,液化砂土大变形引起的上部结构倾斜、倒塌,地下结构上浮、破裂,堤坝滑移、山体滑坡等灾害屡见不鲜.例如,土耳其Adana-Ceyhan地震[2]、土耳其Kocaeli地震[3]、中国台湾Chi-Chi地震[4]以及东日本大地震[5]等,都存在因为土体液化后产生大变形导致的震害.国内外地震震害调查结果表明:由液化大变形引起的建筑物、地下工程等构筑物的破坏经常发生在地震结束后的一段时间.1964年日本新泻地震Shinano河大坝的基础是在地震结束后被摧毁的,1971年美国圣费尔南多大坝也是在地震结束后发生了破坏[6].这些已有震害说明,液化后砂土在地震结束后仍然处于不稳定的状态,在外力及自重应力作用下,液化砂土土体受到的应力大于其强度,液化砂土会呈现出流体的运动状态,因此侧向会产生非常大的流动变形,从而破坏液化区域的工程结构.文献[6-10]分别通过振动台试验或室内三轴试验,证实了液化后的砂土呈现流体的特征.
为此,笔者将液化后砂土视为流体,研究其液化大变形特征.基于VOF(volume of fluid)方法,先后将液化后砂土视为牛顿流体和幂律型剪切变稀非牛顿流体,分析其流动变形,对比分析计算与模型试验,讨论黏度、稠度系数和流动指数对液化砂土的流动变形特征的影响.
1 黏性流体理论及VOF方法
1.1 黏性流体理论
将液化后砂土分别视为牛顿流体和幂律型剪切变稀非牛顿流体,应该满足以下黏性流体方程[11]:
1) 质量守恒方程.质量守恒方程为
(1)

如流体不可压缩,密度ρf为常数,则式(1)为
(2)
2) 动量守恒方程(N-S方程).黏性流体总应力可表示为
(3)

(4)

3) 本构方程.牛顿流体的黏性应力张量表示为
(5)
(6)

幂律型非牛顿流体的黏性应力张量可表示为
(7)
式中:K为稠度系数;n为流动指数.当n<1时,流体为剪切稀化流体;当n>1时,流体为剪切变稠流体;当n=1时,表观黏度为常数,流体为牛顿流体.
将质量守恒方程式(2)和动量守恒方程式(3)进行高斯散度变换,得

(8)
式中:φ为某一变量;n为外法线方向向量;v为速度矢量;Γ为扩散系数;S为源项;A为面积.
将求解区域划分成有限个控制体积,最后利用有限体积法求解上述控制方程.通过压力校正法建立连续方程离散化的压力修正方程,最后,进行压力、速度的耦合处理求解控制方程.
1.2 自由界面求解的VOF方法
VOF方法[12]实际上是利用单元网格中流体与网格体积比函数来描述多种流体流动时自由液面的动态变化.该方法经常用于两种流体流动时追踪流动界面.VOF方法根据体积比函数φ来构造和捕捉自由液面.若φ=1,则表明该单元网格内全部为指定流体;若φ=0,则该单元网格内无指定流体;当0<φ<1 时,则该单元网格内存在流体界面.
将液化后砂土处理为流体,并采用VOF方法追踪自由界面.因此,流体除了满足上述黏性流体基本方程外,流体计算区域还应满足如下VOF方程[13]:
(9)
式中:φ为流体体积比函数;vx,vy分别为流体在x,y方向上的速度分量.
采用施主-受主(donor-acceptor)算法的差分逼近格式求解指定单元体中的体积比函数.图1为非一致的变量配置的Staggered格子.

图1 非一致的变量配置的Staggered格子
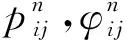
Ω=(xi-1/2,xi+1/2)(yj-1/2,yj+1/2)(tn,tn+1).
(10)
将方程(9)在控制体上积分得
(φn+1-φn)δxδy+Δ(φvx)δtδy+Δ(φvy)δtδx=0,
(11)
定义为
Δ(φvx)δt=min{φAD|Vx|+φf,φDδxD},
(12)
式中:δt为时间步长;φf=max{(1.0-φAD)|Vx|-(1.0-φD)δxD,0};|Vx|=|vxδt|;下标A,D分别表示受主、施主单元,A或D的确定取决于单元网格内自由液面的方向,以及边界上的速度方向;φAD=φA或φD,φA,φD分别表示受主、施主单元网格内流体体积比函数.
同理,可以构造出Δ(φvy)δt.基于上述方法求解出体积比函数φ,就可以追踪流体的自由界面.
2 计算模型
将液化后砂土看作流体,运用VOF方法模拟计算液化砂土的流动变形.液化砂土与空气相互作用的面是一种自由液面,可以根据自由液面的变化捕捉在每个时刻整个流体的流动形状.计算模型和计算网格如图2,3所示.图2中,ad与cd边界为液化砂土与空气接触的交界线,S1面为液化砂土,S2,S3和S4面均为空气.图3中,以1:1的相似比模拟计算物理模型结果如下:模型土箱尺寸为0.95 m×0.33 m×0.35 m,砂土模型尺寸为0.32 m×0.32 m×0.15 m[14].模型网格划分为四边形网格,节点总数为2 016个,单元总数为1 900个.模型左边、右边及底边均为墙边界.

图2 计算模型

图3 计算网格
将液化砂土视为流体来研究其变形问题的核心是液化砂土的流体性质,笔者分别将液化砂土视为牛顿流体和非牛顿流体进行了数值计算.砂土密度取1 600 kg·m-3,其他模型参数见表1.

表1 模型计算参数
3 结果分析与讨论
3.1 计算与试验结果对比
图4为模型试验结果[15].图5,6分别给出了在典型牛顿流体计算模型(黏度η=50 Pa·s)和非牛顿流体计算模型(稠度系数K=600,流动指数n=0.8)条件下流动变形图.由图5,6可知:不同条件下,VOF法均可成功捕捉到液化砂土-空气的边界面,并得到液化砂土的流动变形,成功再现了液化砂土的竖向沉降与水平侧向流滑,其流动变形随着计算时间的增加而增大.模拟过程中,由于模型尺寸的限制,当液化砂土流动到模型最右端时,认为模拟终止.
为了进一步评估液化后砂土的流动特点,选取参考点c对工程应变进行计算分析[15].图7为工程应变参考点示意图.由图7可知:c点为流动之前液化砂土右下角与底边边界交界点,c′点为c点在流动过程中不同时刻的位置;L为砂土初始长度,ΔL为流动增加的长度,并定义工程应变ε=ΔL/L.

图4 模型试验结果

图5 液化后流动构型模拟结果(牛顿流体)

图6 液化后流动构型模拟结果(非牛顿流体)

图7 工程应变参考点示意图
选取试验结果与本研究中4个工况进行对比分析,如图8所示.由图8可知:不同工况下,工程应变的发展趋势一致,基本呈线性发展,但变形发展速度有较大差异;与物理模型试验相比,选取合理的计算参数,如K=1 500,n=0.8,在前期,数值模拟和物理模型试验的工程应变发展基本一致,但流动后期,物理模型试验的工程应变发展较缓慢,造成这种差异变化是因为试验中随流动变形的发展,孔隙水压力消散,有效应力增大,砂土强度恢复,液化砂土的流体性质发生改变,导致其流动变形速度减小,所以需要进一步研究流体本构及流体参数对流动变形的影响.

图8 工程应变随时间变化曲线
3.2 黏度的影响
在牛顿流体模型中,同等条件下,液化后砂土的侧向变形只与黏度有关.笔者分析研究了在3个不同黏度值下液化砂土的流动状态.图9为不同黏度下液化砂土流经P1点的速度-时间曲线,同时给出了模拟终止的时间.

图9 流经P1点的速度-时间曲线
由图9可知:同一黏度值下,流经P1点的流体速度达到最大值后开始逐渐减小,这与液化砂土的流态有关;黏度越低,流动越快,模拟终止需要的时间越少.这是因为黏度越低的液化砂土,其抵抗变形的能力越小;同等前提下,流动速度越快,其变形能力越强.
3.3 稠度系数的影响
正如公式(7)所示,稠度系数K和流动指数n影响幂律型流体的流动变形.K越大,表明流体的表观黏度越大,从而流体抵抗变形的能力越强.图10为非牛顿流体模型在不同稠度系数K时,液化砂土流经P1点速度-时间曲线.由图10可知:经过P1点的速度呈现出先增大后减小的趋势,K不同,液化砂土流动速度有较大差异.总体上来说,K越小,则液化砂土的流动速度越大.图11为不同工况下液化砂土流动到模型最右端所需的时间.由图11可知:在特定的流动指数n下,稠度系数K越小,最先流动到模型最右端.综上,稠度系数K越小,液化砂土抵抗变形能力越弱,流动变形能力越强.
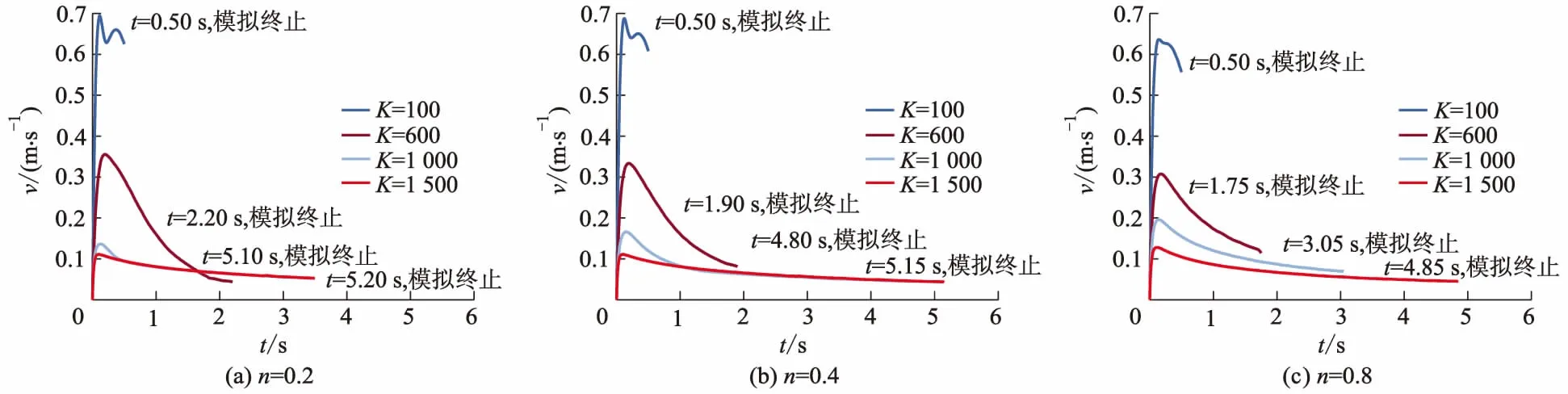
图10 不同稠度系数下P1点速度-时间曲线

图11 不同工况下液化砂土流动到模型最右端所需的时间
3.4 流动指数的影响
对于幂律型非牛顿流体来说,流动指数n越大,表示该流体的非线性越强,抵抗流动变形的能力也就越弱.图12为不同流动指数下,液化砂土流动到模型最右端所需的时间柱状图.图13为不同流动指数下,非牛顿流体模型液化砂土流经P1点的速度时间曲线.由图13可知:不同稠度系数K下,流动指数n对液化砂土流动速度的影响有一定的差异;K较小时,n越大,液化砂土流动速度越小(见图13a);K较大时,n越大,液化砂土的流动速度越大(见图13c,d);K中等值时,前期n越大,液化砂土的流动速度较小,后期n越大,液化砂土的流动速度较大(见图13b).由图12可知:同一K值时,n越大,模拟终止所需时间越短,表明总体上n越大,液化砂土抵抗变形能力越弱,其流动变形能力越强.
综上,流动指数n对液化砂土的流动变形有重要影响,从整体上看,流动指数n越大,液化砂土的流动速度越大,但流动指数n对液化砂土流经局部的速度的影响较为复杂.

图12 不同流动指数下液化砂土流动到

图13 不同流动指数下P1点速度-时间曲线
4 结 论
1) 通过VOF方法,对液化后砂土进行流动变形分析,模拟结果基本上可以呈现液化砂土的流动特性,能够重现试验中液化砂土的流动特点,验证了本研究方法的正确性.
2) 将液化砂土视为牛顿流体,流动变形大小以及速度都随着黏度增大而减小;将液化砂土视为剪切变稀非牛顿流体,流动变形比较复杂,同时受稠度系数以及流动指数的影响.整体上,稠度系数越大,流动指数越小,液化砂土的流动变形及速度越小.
3) 液化砂土的流体特性显著影响其流动变形特征,因此需进一步研究分析液化砂土的流体特性,并结合物理模型试验及液化变形调查资料来验证该方法的普适性.
参考文献(References)
[ 1 ] 浜田政則, 安田進, 磯山龍二, 等. 液状化による地盤の永久変位の測定と考察[J]. 土木学会論文集, 1986, 376: 211-220.
[ 2 ] ADALIER K, AYDINGUN O. Liquefaction during the June 27, 1998 Adana-Ceyhan (Turkey) earthquake[J]. Geotechnical and Geological Engineering, 2000, 18(3): 155-174.
[ 3 ] SONMEZ B, ULUSAY R. Liquefaction potential at Izmit Bay: comparison of predicted and observed soil liquefaction during the Kocaeli earthquake[J]. Bulletin of Engineering Geology and the Environment, 2008, 67(1): 1-9.
[ 4 ] YUAN H M, YANG S H, ANDRUS R D, et al. Liquefaction-induced ground failure: a study of the Chi-Chi earthquake cases[J]. Engineering Geology, 2004, 17(1/2):141-155.
[ 5 ] TOWHATA I, GOTO S, TAGUCHI Y, et al. Liquefaction consequences and learned lessons during the 2011Mw=9 gigantic earthquake[J]. Indian Geotechnical Journal, 2013, 43(2): 116-126.
[ 6 ] 陈育民, 刘汉龙, 周云东. 液化及液化后砂土的流动特性分析[J].岩土工程学报, 2006, 28(9):1139-1143.
CHEN Y M, LIU H L, ZHOU Y D. Analysis on flow characteristics of liquefied and post-liquefied sand [J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9):1139-1143. (in Chinese)
[ 7 ] SASAKI Y, TOWHATA I, TOKIDA K I, et al. Mechanism of permanent displacement of ground caused by seismic liquefaction[J]. Soils and Foundations, 1992, 32 (3):79-96.
[ 8 ] TOWHATA I, VARGAS-MONGE W, ORENSE R P, et al. Shaking table tests on subgrade reaction of pipe embedded in sandy liquefied subsoil[J]. Soil Dynamics and Earthquake Engineering, 1999, 18:347-361.
[ 9 ] HAMADA M, WAKAMATSU K. A study on ground displacement caused by soil liquefaction[J]. Journal of Geotechnical Engineering, 1998, 596: 189-208.
[10] 周恩全, 王志华, 陈国兴,等. 饱和砂土液化后流体本构模型研究[J]. 岩土工程学报, 2015, 37(1):112-118.
ZHOU E Q, WANG Z H, CHEN G X, et al. Constitutive model for fluid of post-liquefied sand [J]. Chinese Journal of Geotechnical Engineering, 2015, 37(1):112-118.(in Chinese)
[11] 王献孚,熊鳌魁. 高等流体力学[M]. 武汉:华中科技大学出版社,2004.
[12] 岳戈. ADINA流体与流固耦合功能的高级应用[M]. 北京:人民交通出版社,2010.
[13] 刘儒勋,舒其望. 计算流体力学的若干新方法[M]. 北京:科学出版社,2003.
[14] 黄雨,郝亮,谢攀,等.土体流动大变形的SPH数值模拟[J]. 岩土工程学报,2009,31(10):1520-1524.
HUANG Y,HAO L,XIE P, et al. Numerical simulation of large deformation of soil flow based on SPH method [J]. Chinese Journal of Geotechnical Engineering, 2009, 31(10):1520-1524. (in Chinese)
[15] HUANG Y, MAO W W, ZHENG H, et al. Computational fluid dynamics modeling of post-liquefaction soil flow using the volume of fluid method[J]. Bulletin of Engineering Geology and the Environment, 2012, 71(2): 359-366.

