露出型钢柱脚低多层钢框架结构动力响应机理

包恩和, 王天成, 孙凌云

(1. 桂林理工大学 土木与建筑工程学院, 广西 桂林 541004; 2. 广西大学 土木建筑工程学院, 广西 南宁 530004; 3. 贺州学院 建筑工程学院, 广西 贺州 542899)

露出型钢柱脚具有施工简单、成本低等特点,在低多层钢结构工程中得到广泛应用.低多层钢结构在工程设计时,露出型钢柱脚视为铰接计算,且忽略柱脚处弯矩作用,柱脚设计的安全性欠佳.实际上,露出型钢柱脚通过锚栓和垫板与基础进行连接，具有一定的转动约束,可传递部分弯矩,在工程设计时应按半刚性连接计算,露出型钢柱脚力学性能介于铰接与刚接之间.因此,准确评价露出型钢柱脚的强度、刚度及耗能机理对低多层钢结构抗震设计有工程意义.

文献[1-3]对露出型钢柱脚的抗震性能试验、有限元分析、理论分析等进行综合分析,得到处于受剪状态和剪力与轴力耦合作用状态时钢柱脚的弯矩-转角的滑移型滞回曲线规律和耗能性能,并提出露出型钢柱脚的抗剪承载力公式.文献[4-5]通过试验研究,研发了具有优良抗震性能的新型减震露出型钢柱脚.文献[6-8]以柱脚形式(刚接、铰接)为主要研究参量,对不同结构形式多层钢结构进行非线性时程分析,研究了多层钢结构动力响应机理.文献[9]通过静力推覆分析,探讨强度系数对露出型钢柱脚的受力与变形等的影响.综上可知,以往关于露出型钢柱脚的研究虽然很多,但有关露出型钢柱脚低多层钢框架结构动力响应机理的研究鲜有报道.

为此,本研究首先定义考虑变动轴力影响的露出型钢柱脚滑移型滞回曲线模型,以框架形状、露出型钢柱脚强度系数为主要研究参量,建立13个低多层规则钢框架模型,通过弹塑性时程分析,研究动力响应机理.

1 分析模型

分析模型为由箱形截面型钢柱、H型钢梁及露出型钢柱脚组成的钢框架结构.分析模型的柱、梁均刚接,柱、梁、柱脚锚栓及柱脚垫板分别采用Q295,Q235,Q490和Q345钢.模型标准层平面图如图1所示.模型跨度均为7.2 m,层高均为4.0 m,首层、标准层及顶层的单位负载分别为7.6,7.5及8.1 kN·m-2.

模型主要研究参量有框架形状和露出型钢柱脚强度系数.分析模型的框架形状有单跨3层、单跨6层和双跨3层.各模型的首层剪重比CB均为0.3(其中,CB=Vu/W,W为模型总重力荷载,Vu为结构承载能力极限状态时的首层剪力).根据文献[9]可知,露出型钢柱脚强度系数γ的计算公式如下所示：

γ=BMP/CMP,

(1)

式中：BMP为不考虑轴向力作用的露出型钢柱脚屈服弯矩；CMP为首层柱底端全截面的屈服弯矩.

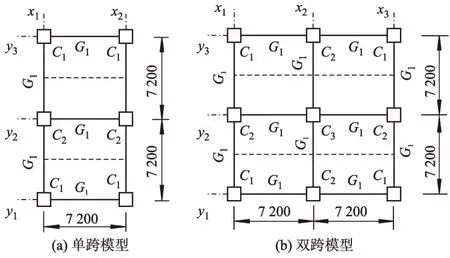
图1 分析模型标准层平面布置(单位： mm)

各模型露出型钢柱脚与基础进行锚固时,采用不同直径(22～36 mm)的锚栓,调整露出型钢柱脚强度系数,模型露出型钢柱脚强度系数为0.28～1.20.另外,分析模型的第i层强柱系数αi的定义公式如下所示:

(2)

式中:B-CMP(i+1)为第i+1层柱脚的全截面塑性弯矩,T-CMP(i)为第i层柱头的全截面塑性弯矩;L-BMP(i)和R-BMP(i)分别为第i层梁左、右端全截面塑性弯矩.

模型的强柱系数αi设置较大(顶层1.6以上,其他层2.0左右),地震反应中尽量避免强柱系数的影响.

各模型以结构层数、结构跨度数、露出型钢柱脚强度系数和结构基本周期(s)的方法对各模型进行命名.共13个分析模型,各分析模型主要参数见表1.

表1 模型主要参数

2 露出型钢柱脚相关参数

为确保受力过程中露出型钢柱脚锚栓先于垫板屈服,垫板厚度取1.3d′(d′为锚栓直径),锚栓埋入基础的锚固长度为20d′.模型分析中采用抗弯弹簧换算钢柱脚的强度和刚度.

露出型钢柱脚变形关系如图2所示.根据图2可知,钢柱脚转角θ的定义公式如下:

(3)

式中:u1,u2分别为柱翼缘的垂直位移;D为柱宽.

图2 钢柱脚变形关系

考虑变动轴力影响的露出型钢柱脚弯矩-转角的滑移型滞回曲线关系如图3所示.

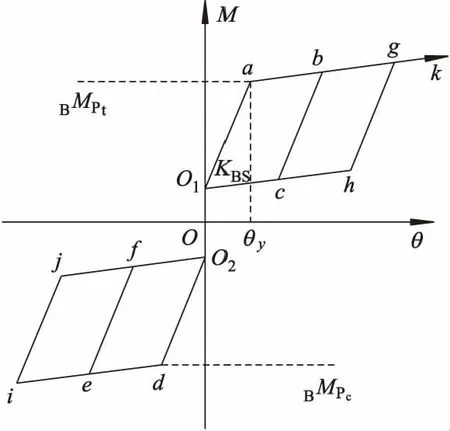
图3 钢柱脚弯矩-转角滞回曲线

滑移型滞回曲线的先后滑移顺序依次为O，O1，a，b，c，O1，O，O2，d，e，f，O2，O，O1，c，b，g，h，O1，O，O2，f，e，i，j，O2，O，O1，h，g，k.

外荷载作用下,露出型钢柱脚的垫板和钢筋混凝土基础保持一体状态时钢柱脚刚度很大,本研究中假设为无穷大.根据文献[10],在外荷载作用时,露出型钢柱脚垫板与钢筋混凝土基础分离后的弹性刚度KBS公式为

(4)

式中:E为弹性模量;n为受拉锚栓总数;A为单个锚栓截面积;dt为受拉侧锚栓截面中心到柱截面中心的距离;dc为受压侧柱外缘到柱截面中心的距离;lb为锚栓长度.

根据文献[9],柱轴力N为压力时,钢柱脚的屈服弯矩公式为

BMPc=nAσy(dt+dc)+Ndc;

(5)

柱轴力N为拉力时,屈服弯矩公式为

BMPt=2nAσydt-Ndt，

(6)

式中σy为单个受拉锚栓屈服强度.

各模型露出型钢柱脚受力及其构造示意图如图4所示.

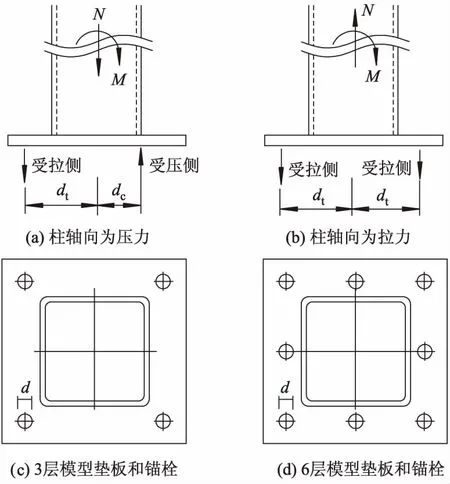
图4 模型露出型钢柱脚受力及其构造示意图

3 二阶非线性时程分析

3.1 分析方法

考虑二阶非线性因素，且基于塑性铰理论，设计了分析程序clap,利用该程序对各模型Y1榀框架进行时程分析,计算原理见文献[11].各模型竖向荷载集中作用于各层柱顶及梁跨中,各层柱顶竖向荷载作用于边柱及中柱,顶层竖向荷载分别为52.5,105.0 kN·m-2,标准层分别为48.6,97.3 kN·m-2,首层分别为49.3,98.5 kN·m-2.在各层梁的跨中位置,顶层竖向荷载为105.0 kN·m-2,标准层为97.3 kN·m-2,首层为98.6 kN·m-2.各模型柱、梁的滞回曲线模型为双线型,露出型钢柱脚的滞回曲线模型为滑移型,柱、梁及露出型钢柱脚屈服后的刚度均为初刚度的1/100;框架阻尼矩阵采用刚度比例型,阻尼系数为0.02.

地震波选用El Centro (1940) NS 和 JMA Kobe(1995)NS,两者强度等级对应于设防烈度地震的地动最大速度为50 cm·s-1(分别用E2,K2表示),对应于罕遇地震的地动最大速度为75 cm·s-1(分别用E3,K3表示).地震波参数见表2.其中，各模型时程分析的持续时间均为地震波的前20 s.

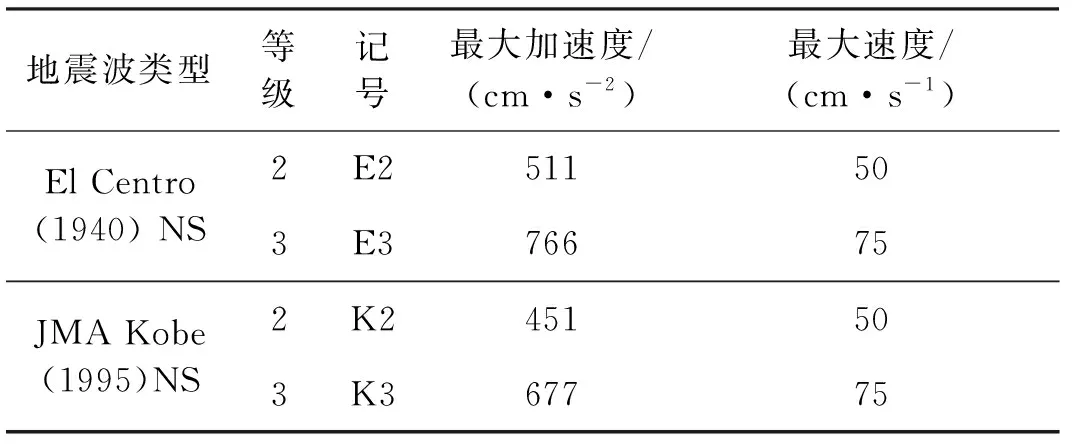
表2 地震波参数

3.2 地震分析结果

3.2.1 最大层间位移角

图5表示不同的露出型钢柱脚强度系数条件下各模型最大层间位移角的变化情况,其中R为最大层间位移角.

由图5可知:随强度系数减小,各模型首层R值增大,第2层R值减小；3层模型强度系数≤0.6时,首层变形集中较大,例如,在罕遇地震E3,K3作用下,模型④,⑧及⑨的首层R值最大,R=0.04 rad;强度系数≥0.7时,3层模型最大层间位移角分布较均匀；另外,6层模型最大层间位移角分布较均匀,在罕遇地震E3，K3作用下,R≈0.02 rad.设防烈度地震E2,K2作用下各模型最大层间位移角R值分布趋势接近罕遇地震E3,K3作用时的R值分布.

图5 层间位移角最大值变化情况

综上,强度系数大小对低层(3层)模型钢框架结构层间位移分布的影响较多层(6层)显著,尤其是强度系数≤0.6时更为明显.

3.2.2 各模型塑性变形能量

图6为地震波E3,E2作用下,各模型首层(包括露出型钢柱脚、首层柱底端以及柱顶、首层梁)、2层、3层及4-6层(6层模型)等吸收的塑性变形能量分布.

由图6a,b可知,罕遇地震E3作用下, 3层模型塑性变形能量主要集中在首层,首层的塑性变形能量占模型总塑性变形能量的70%～80%.露出型钢柱脚强度系数越小,首层塑性变形能量比例有增大趋势,增幅小于5%.强度系数小于1.0的各模型露出型钢柱脚的塑性变形能量比例也在增大(塑性变形比例为3%～15%),首层梁塑性变形能量比例有减小趋势(塑性变形比例为20%～70%);强度系数大于1.0的模型,露出型钢柱脚保持弹性状态,首层柱底端形成塑性铰(塑性变形能量比例为5%～10%).低层(3层)模型的跨形变化(单跨、双跨)对各模型塑性变形能量分布规律影响不明显.

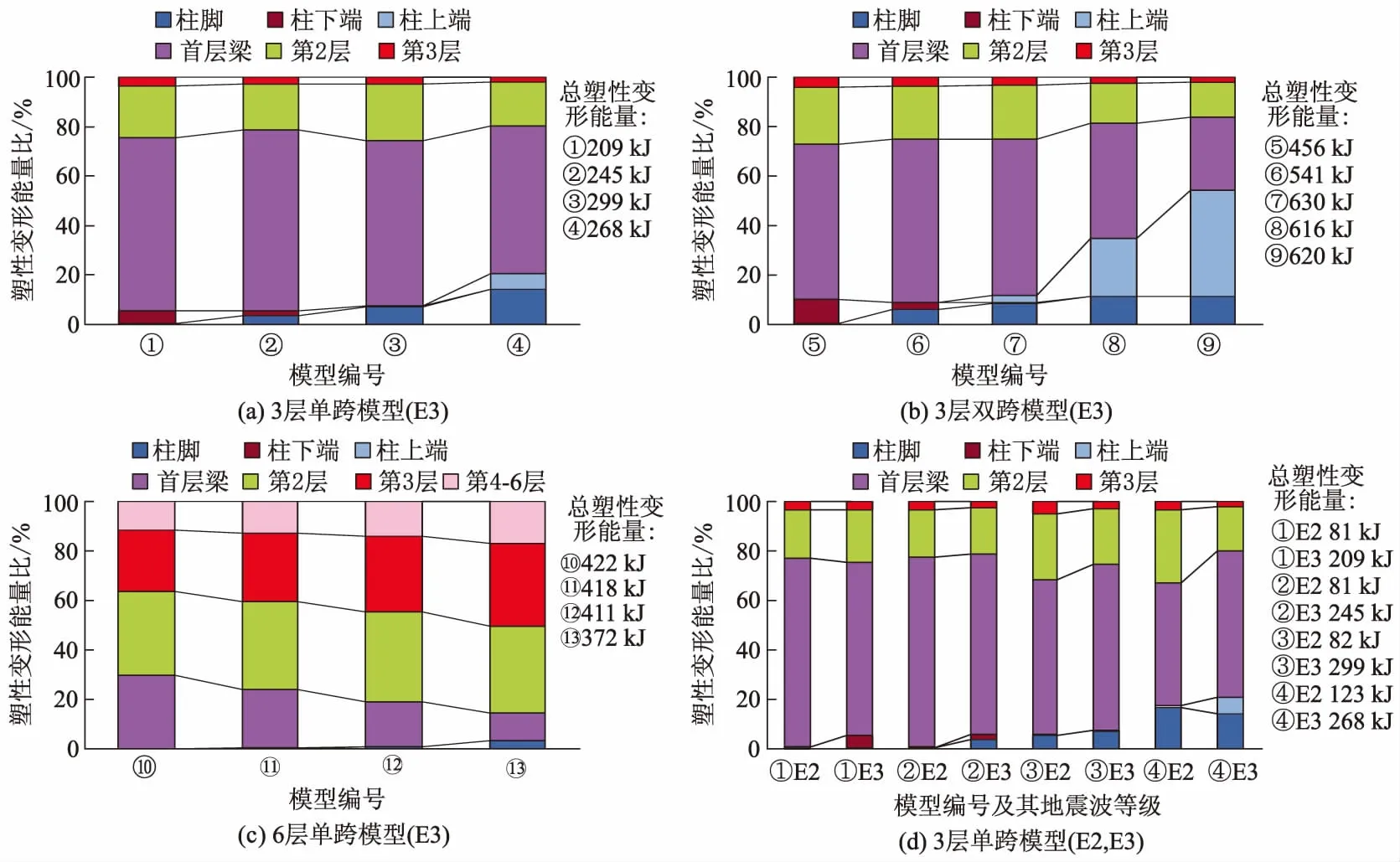
图6 各模型塑性变形能量分布

由图6c可见,罕遇地震E3作用下,多层(6层)模型塑性变形能量在2,3层呈集中的趋势,强度系数越小,基本上2,3层塑性变形能量比例越大,其比值约占模型总塑性变形能量的60%.首层的塑性变形能量比值减小,例如,6层模型中强度系数最小的模型,首层的塑性变形能量占模型总塑性变形能量的15%.

由图6d可知:强度系数大于0.8(锚栓规格M36,M30)时,模型的各层塑性变形能量比例一致,不受地震强度作用的影响;强度系数小于0.7(锚栓规格M27,M22)的模型,罕遇地震E3作用下,塑性变形能量向首层集中更明显.

3.2.3 露出型钢柱脚滞回曲线关系

图7-10为地震波E3作用下部分模型的露出型钢柱脚滞回曲线，其中,θ为转角.图7中横坐标为露出型钢柱脚转角θ,纵坐标为露出型钢柱脚弯矩荷载与首层柱底端全截面屈服弯矩比值M/CMP.图8中横坐标为露出型钢柱脚弯矩荷载与首层柱底端全截面屈服弯矩比值M/CMP,纵坐标为露出型钢柱脚轴向荷载与首层柱底端全截面屈服轴力比值N/CNP.图9为露出型钢柱脚(锚栓规格M22)M/CMP-θ滞回曲线.图10为露出型钢柱脚(锚栓规格M22)N/CNP-M/CMP滞回曲线.

图7 露出型钢柱脚(锚栓直径M36)M/CMP-θ滞回曲线

图8 露出型钢柱脚(锚栓直径M36)N/CNP-M/CMP曲线

图9 露出型钢柱脚(锚栓直径M22)M/CMP-θ滞回曲线

图10 露出型钢柱脚(锚栓直径M22)N/CNP-M/CMP滞回曲线

图7-8可知,3层单跨模型①和3层双跨模型⑤ (各模型钢柱脚强柱系数大于1.0,锚栓规格M36)的钢柱脚保持弹性状态,这主要是由于模型⑤ 的中柱轴压力大于边柱轴压力,而模型⑤ 的中柱受拉区抗弯强度与边柱相比偏大.E3作用时,6层单跨模型⑩ 的层间位移均匀分布,首层及露出型钢柱脚变形都较小,钢柱脚保持弹性.综上,钢柱脚处于弹性状态时的动力响应值较好地吻合露出型钢柱脚屈服弯矩定义公式.

图9-10可知,3层单跨模型④、3层双跨模型⑧及6层单跨模型(各模型钢柱脚强柱系数小于0.5,锚栓规格M22)在罕遇地震E3作用下,钢柱脚有较大的塑性变形.各模型露出型钢柱脚M/CMP-θ关系曲线为滑移型滞回曲线,柱轴向受压时钢柱脚屈服弯矩大于理论值BMP,随柱轴向受压力增大,露出型钢柱脚屈服弯矩响应值增大.在弯矩M作用下,3层模型的露出型钢柱脚受拉区和受压区对应的动力响应屈服弯矩都大于理论值BMP,同时钢柱脚受压区屈服弯矩都大于受拉区;3层双跨模型中柱钢柱脚受拉区屈服弯矩大于边柱钢柱脚受拉区.6层单跨模型的露出型钢柱脚受拉区动力响应屈服弯矩都小于理论值BMP,这是因为钢柱脚受拉区变形较大时柱轴向承受拉力.

露出型钢柱脚弹塑性动力响应滞回曲线的形状和屈服弯矩等分别吻合本研究中提出的考虑变动轴力影响的露出型钢柱脚弯矩-转角的滑移型滞回曲线的形状和钢柱脚屈服弯矩定义公式.

4 结 论

1) 随露出型钢柱脚强度系数减小,各模型首层位移角增大,而第2层层间位移角减小;3层模型露出型钢柱脚强度系数≤0.6时,首层变形集中较大;强度系数≥0.7时,3层模型最大层间位移角分布趋于均布;6层模型最大层间位移角分布较均匀,露出型钢柱脚强度系数影响不明显.

2) 3层模型塑性变形能量主要集中在首层,占模型总塑性变形能量的80%.但是,首层塑性变形能量主要集中在梁端,模型的跨形变化对3层模型塑性变形能量分布影响不明显.6层模型塑性变形能量分布趋于均匀.

3) 露出型钢柱脚弹塑性动力响应滞回曲线的形状和屈服弯矩等分别较好地吻合本研究中提出的露出型钢柱脚滑移型滞回曲线模型和钢柱脚屈服弯矩定义公式.

参考文献(References)

[ 1 ] 韩宝仪,李维平,田成钢,等.露出型钢柱脚抗剪承载力的试验研究[J].钢结构,2014,29(1):8-12.

HAN B Y,LI W P,TIAN C G,et al. Experimental research of shear capacity in steel column bases[J]. Steel Construction,2014,29(1):8-12.(in Chinese)

[ 2 ] 宋岩,王永.轴向力对外露式刚性柱脚抗震性能的影响[J].世界地震工程,2011,27(1):131-135.

SONG Y,WANG Y. Research on the seismic perfor-mance of exposed column footing connection joint under axial loading[J]. Word Earthquake Engineering,2011,27(1):131-135.(in Chinese)

[ 3 ] YAMANISHI T,TAKAMATSU T,TAMAI H,et al. Hysteresis model and restoring force characteristics of non-slip-type exposed column-base subjected to variable axial-force and bending[J]. Journal of Structural and Construction Engineering, 2012, 77:1755-1762.

[ 4 ] 胡郢,雷劲松,罗文霞.新型钢柱脚抗震性能分析[J].世界地震工程,2011,27(1):115-120.

HU Y,LEI J S,LUO W X. Researches on seismic behaviors of a new kind of steel column base[J]. World Earthquake Engineering, 2011,27(1):115-120. (in Chinese)

[ 5 ] 雷劲松,姚勇,卢学松,等.带楔块装置钢柱脚恢复力特性试验[J].建筑结构,2011,41(8):83-86.

LEI J Y,YAO Y,LU X S,et al. Experimental study on restoring force characteristics of steel column base with wedge device[J]. Building Structure,2011,41(8):83-86. (in Chinese)

[ 6 ] 包恩和,黄美玲,曹邕生,等.多层规则钢框架连体结构动力响应机理研究[J].科学技术与工程,2015,15(33):79-84.

BAO E H,HUANG M L,CAO Y S,et al. Study on the dynamic responses mechanism of multistory inerratic steel frame connection structure[J]. Science Technology and Engineering,2015,15(33):79-84.(in Chinese)

[ 7 ] 陈宜虎,赵艳林,包恩和,等.多层屈曲约束斜撑钢框架抗震性能研究[J].同济大学学报(自然科学版), 2016,44(4):512-519.

CHEN Y H,ZHAO Y L,BAO E H,et al. Seismic research on multi-story buckling restrained braced steel frame[J]. Journal of Tongji University (Natural Science),2016,44(4):512-519. (in Chinese)

[ 8 ] 包恩和,陈宜虎.多层屈曲约束支撑钢框架抗震性能研究[J].结构工程师,2013,29(6):98-105.

BAO E H,CHEN Y H. Seismic response of multi-layer buckling restrained braced steel frame[J]. Structural Engineers,2013,29(6):98-105.(in Chinese)

[ 9 ] 包恩和,李风勇,李丽,等.露出型钢柱脚强度对低多层规则钢框架抗震性能的影响[J].科学技术与工程,2016,16(17): 93-99.

BAO E H,LI F Y,LI L,et al. Influence of strength of exposed steel column foot to anti-seismic performance of steel frames of low-layer and multi-layer[J]. Science Technology and Engineering,2016,16(17):93-99. (in Chinese)

[10] 日本建筑学会.钢构造接合部设计指针[M].东京:丸善株式会社,2006:255-260.

[11] OGAWA K,TADA M.Combined non-linear analysis for plane frame (clap)[C]∥Architectural Institute of Japan. Proceeding of 17th Symposium on Computer Technology on Information Systems and Applications.Tokyo:Showa Intelligence Press,1994:79-84.