基于水头自适应的可逆机组导叶关闭规律研究

徐建林，何中伟

(1.浙江省水利水电建筑监理公司，杭州 311600；2.华东勘测设计研究院，杭州 311100)

在可逆式机组中，因转速或者开度的细微变动，就能改变水流流态，引发水力干扰，从而引起流量的巨大变幅继而在输水系统中发生较大的水锤压力[1]，影响可逆机组的运行安全。在不额外增加经济投资前提下，合理的优化选择导叶关闭规律是抽水蓄能电站一种有效、安全、经济的防护措施[2, 3]。目前，可逆式机组主要采用常规的直线关闭、延时关闭和折线关闭[4]。国内钻研主要有：陈丹以具体的工程实例，剖析了不同导叶关闭规律对机组尾水管真空度的影响[5]，以及王丹、杨建东等人通过具体电站验算，指明发生蜗壳最大动水压力的极值点是流量梯度变化最大的工作点的这一内在规律[2]。前人研究很少有以水头为探讨对象来研究过流特性[6]，多为根据某固定单一工况运用不同优化方法进行的优化，通常，优化工况为在最大水头和设计水头下进行甩全负荷并过渡过程计算,但文献[2, 7]分析指出：不仅在最大水头甩全负荷工况下蜗壳和管道最大水压力并不一定出现，而且优选出的导叶关闭规律是根据机组运行范围内最大相对开度来确定的，文献[8]指出机组满负荷运行时的导叶开度根据工况运行水头的变化而相应变化。虽然黄贤荣等人虽然针对水头研究[9, 10]，芦月针对抽水蓄能电站不同水头下导叶关闭规律做了研究[11]，分析指出分别对于高水头、中水头、低水头不同电站采取不同的关闭规律，樊红刚等人研究提出利用多工况优化[12]，但实例单薄，分析不具体。本文以宁海抽水蓄能电站为例，通过充分利用现代微机调速器的功能，实现水头在实时采集，针对不同工况的工作水头，匹配不同的导叶关闭规律进行过渡过程计算，以此增加机组的安全性。

1 数学模型

1.1 调节保证计算机组转速变化

在调节过程当中，机组进行紧急停机甩负荷时，负载力矩突变为0，由此形成可逆式机组的能量不平衡，诱使机组转速开始上升，转速上升率公式为[4]：

(1)

式中：N0为机组初始状态所载负荷;f为修正系数;n0为机组初始转速;GD2为机组转动惯量;Ts1为导叶开度由全开关至空载开度的所需的时间，与导叶关闭时间Ts有关，混流式和水斗式：Ts1=(0.8 ～0.9)Ts，轴流式：Ts1=(0.6 ～0.7)Ts。

根据上式可以看出，机组转速上升率β随着导叶关闭Ts时候的减小而越小。

1.2 蜗壳进口水锤压力变化

假设流动具有非定常性且流体不可压缩，则水流在机组中满足以下控制方程[13]：

(2)

式中：x为距离；t为时间；V为速度；p为压力；ρ为密度；f为摩擦因子；a为倾角。

1.3 尾水管真空度变化

在非恒定流情况下，由公式可得到尾水管真空度[14]为：

(3)

1.4 调速器水位采集与水头计算

文献[8]给出，在现有的微机调速器基础上，将电厂的上、下游水位送到公用的LCU，并经过可靠性转换精度高的A/D模块转换成数字信号。只要再把数字信号经D/A模块转换为模拟信号送到调速器的A/D采集模块，就可计算出相应的实时水头，以此来实现水头的自适应。

2 可逆机组关闭规律

针对抽水蓄能可逆式机组，其关闭规律可被分为：常规关闭规律和自适应关闭规律。常规关闭规律指的是，机组在最大水头或设计水头甩负荷工况下通过整定优化出单一固定的导叶关闭规律，在机组发生甩负荷工况时，按照优化过的关闭规律关闭导叶；自适应关闭规律指，导叶关闭规律在不同的工况下，以实际的运行参数来采取相应的导叶关闭规律。本文采取根据不同运行工况的水头来实现导叶自适应关闭。

3 算例分析

3.1 基本资料

以宁海抽水蓄能电站为例，电站总装机容量700 MW，电站布置为一洞双机布置，引水系统为圆形有压隧洞，总长1 171.4 m，岔管前隧洞直径与引水支管直径分别为5.6、3.5 m，尾水系统为两机共用尾水系统，由压力钢管、调压井和尾水隧洞组，成总长约928.9 m。各台机组额定转速、额定出力、额定水头分别为428.60 r/min、 357.14 MW、459 m，水轮发电机GD2为5 800 t/m2，电站管道基本布置图与管道参数见图1和表1。

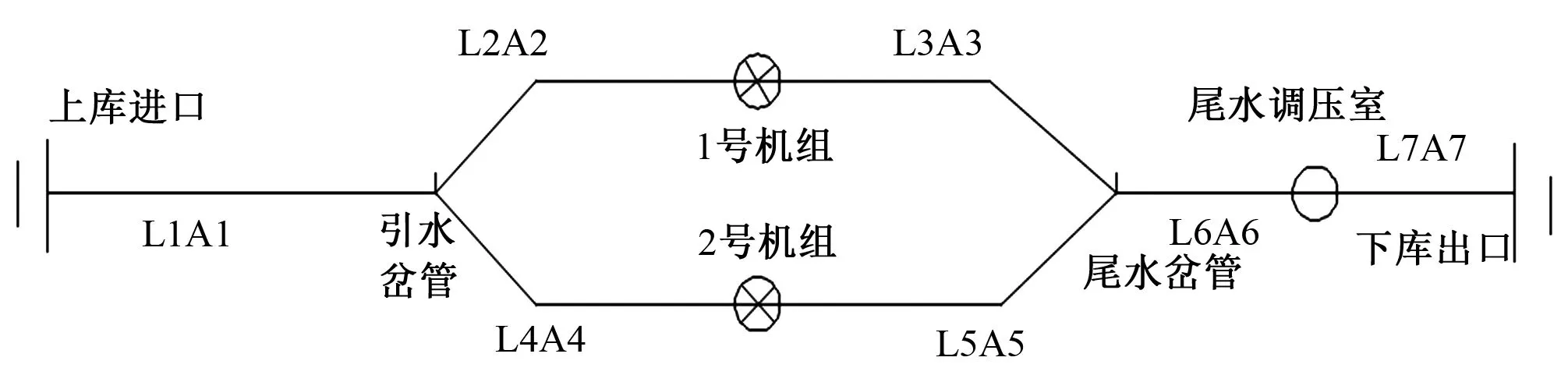
图1 简化后的系统布置示意图Fig.1 Layout of the hydropower station after simplify

位 置管道特性参数长度/m面积/m水头损失系数上库进水口至分叉点1103.9230.190.000 149分叉点至1号机组96.599.060.000 6391号机组至下游分叉点216.7021.300.000 136分叉点至2号机组99.409.060.000 6192号机组至下游分叉点208.4321.300.000 127下游分叉点至尾水调压室20.0045.360.000 003尾水调压室至下库进水口740.6145.360.000 037

3.2 计算工况选择及调保计算要求

据电站设计要求，关闭规律应该满足以下调节保证计算允许值：机组蜗壳最大水压力值H蜗壳max≤748.80 m；机组最大转速上升率β机组max≤45%;尾水管最小内水压力H尾水min≥12.10 m。

根据表2计算3种工况，在发电工况下选取在额定转速计算发电工况大波动过渡过程，具体工况选择如表2所示。

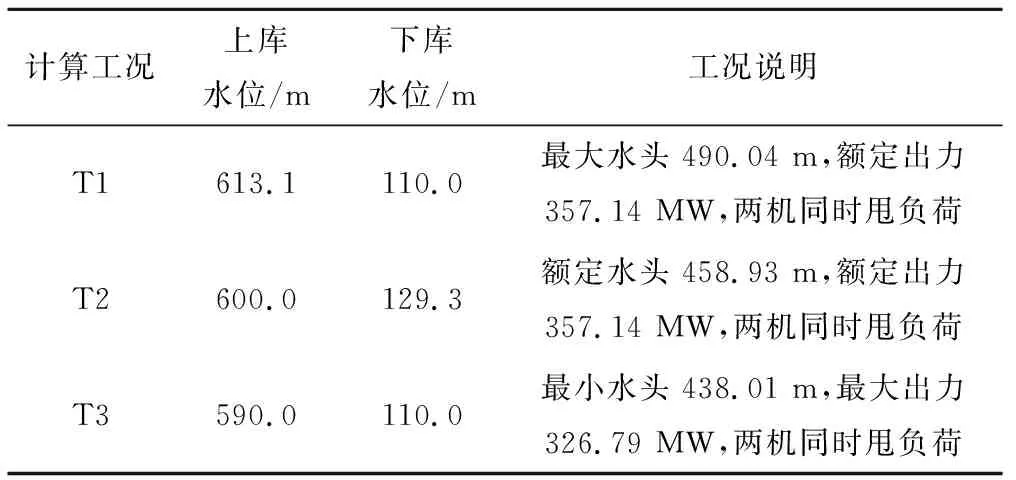
表2 大波动过渡过程计算工况选择Tab.2 Calculation condition selection of big fluction transition process

3.3 不同水头下大波动过渡过程计算比较

工况T1：在保证相同的有效的关闭时间下，直线采取20 s直线关闭，延时8 s直线关闭、延时9 s直线关闭、延时10 s直线关闭规律，关闭规律如图2所示。

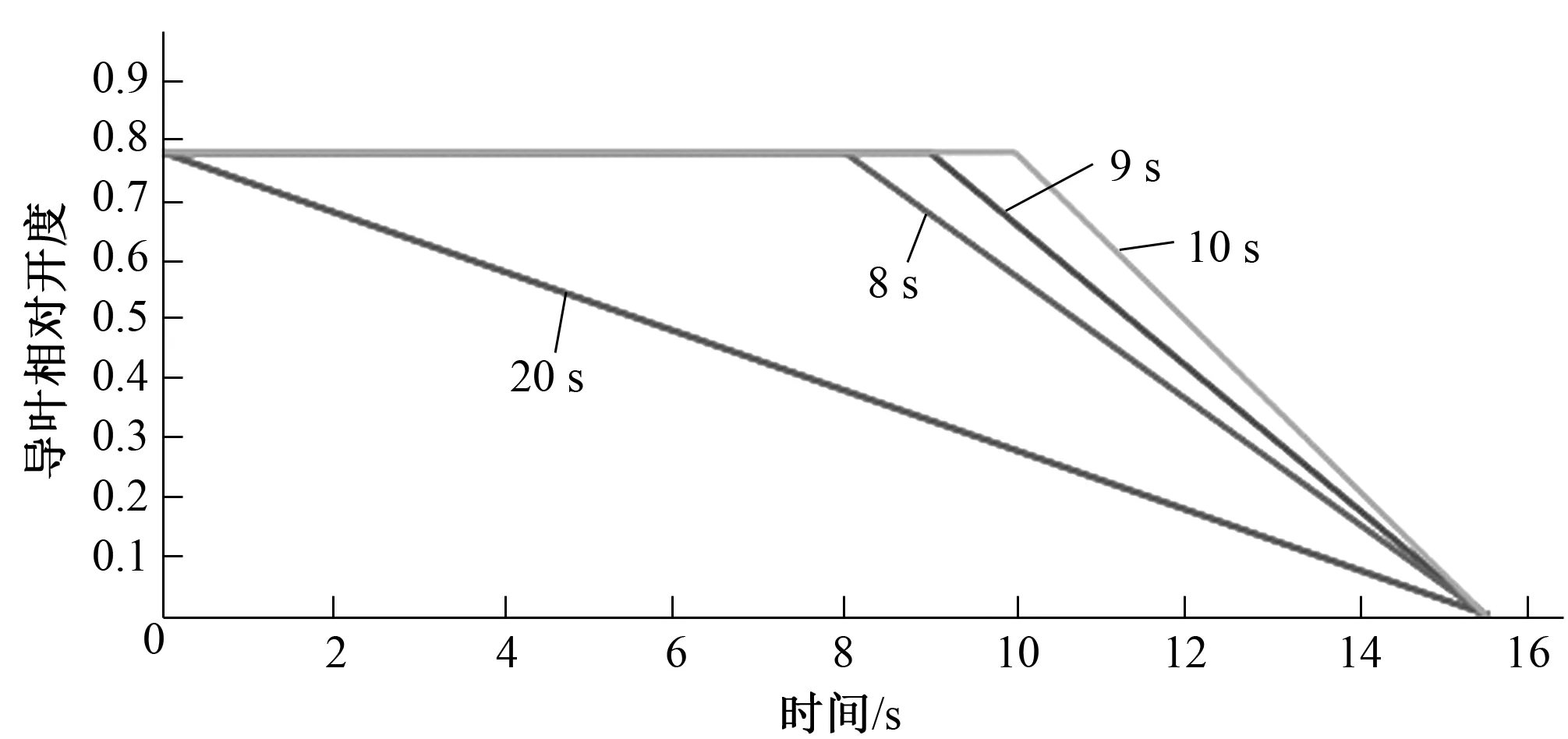
图2 导叶关闭规律Fig.2 Wicket gate closing rate 注：有效关闭时间=延时时间+导叶直线关闭实际时间

工况T1采取简单的直线关闭和延时直线关闭规律对比结果如表3所示，根据表3可看出：① 20 s直线关闭，从优化结果看出，机组最大转速上升率β机组max和尾水管最小水压力H尾水min分别为35.69%和44.30 m，均满足设计要求，但是机组蜗壳最大水压力值H蜗壳max为760.58 m，超过了压力允许值748.80 m，故对于该工况，简单的20 s直线关闭规律远远无法达到调保计算要求；②如图3所示，是延时直线关闭规律及其优化结果对比。由图3可得：伴随延时时间的增大，机组蜗壳最大水压力升高和机组最大转速上升两者的鲁棒性很强，没有呈现出明显变化，而尾水管最小水压力远远达到调保要求值。

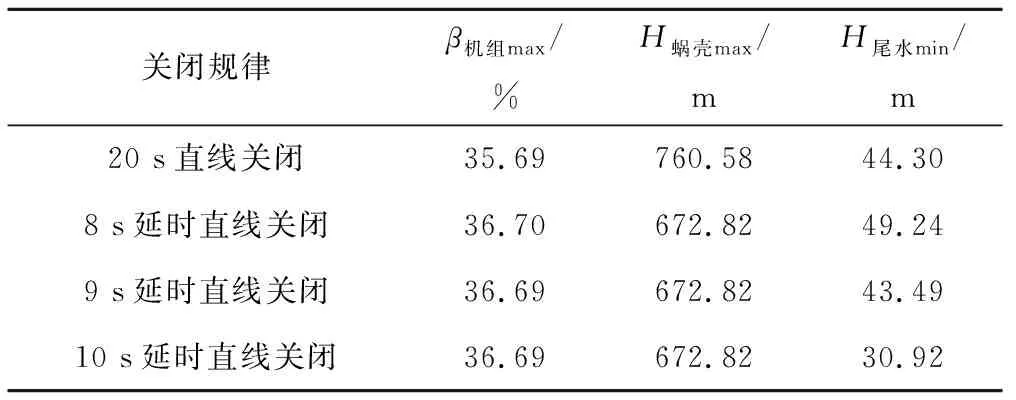
表3 不同导叶关闭规律及其优化计算结果对比(T1)Tab.3 Comparison results of different closing law(T1)

注：β机组max为机组最大转速上升；H蜗壳max为蜗壳最大水压力；H尾水min为尾水管最小水。

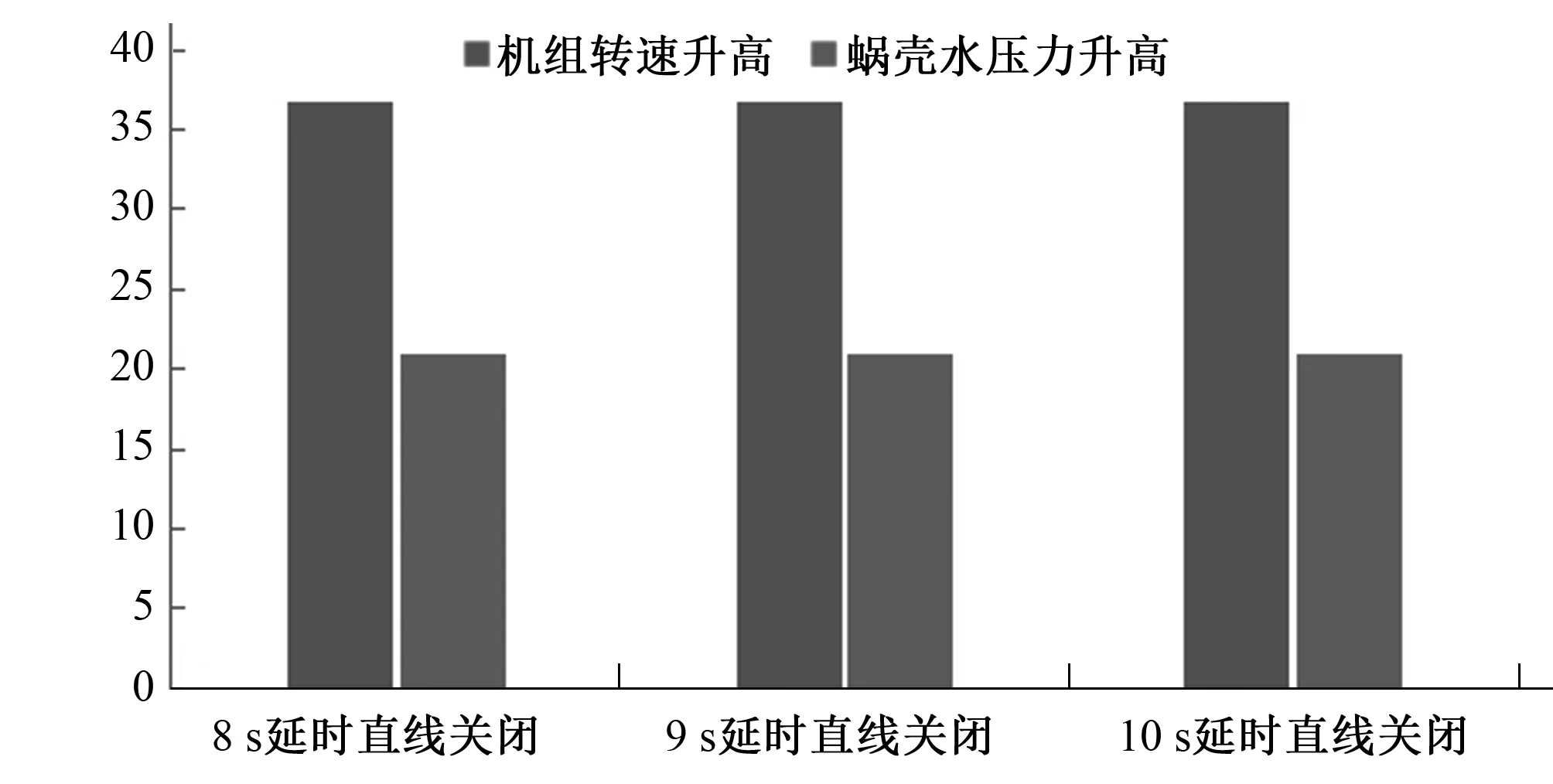
图3 延时直线关闭规律及其优化结果对比Fig.3 Comparison results of delay line closing law 注 :蜗壳水压力升高=(蜗壳水压力最大值-甩负荷前水压力值)/甩负荷前水压力值。

9 s延时直线关闭规律和20 s直线关闭规律的甩负荷过渡过程计算结果如图4所示，根据文献，开度和转速两者的变化决定可逆式机组其流量变化[15]：

(4)

式中：y为机组导叶的相对开度;n为机组转速;Q为机组流量。

由图4(a)可看出20 s直线关闭规律的蜗壳最大水压力(760.58 m)远远大于9 s延时直线关闭下的蜗壳最大水压力(672.82 m)。结合上式和甩负荷后的机组运行轨迹线图4(b)(9 s延时直线关闭：从初始点1顺时针向点2、3、4变化；20 s直线关闭：从初始点1顺时针向点5、6、7变化)可看出，在可逆式机组甩负荷过渡过程中，伴随不同的导叶关闭规律，在机组流量特性曲线上的轨迹线上呈现出较大差别。①在9 s延时直线关闭下，当机组接到甩负荷指令后，机组立刻进行甩负荷，导叶紧急关闭，机组转速立即升高，从点1到点2，因导叶延时9 s不动，流量随导叶的变化为0，此时机组流量变化完全等于上式右边的第二项,而对于20 s直线关闭规律，从点1到点5，由于机组导叶及时关闭，流量随导叶的变化不为0，机组的流量变化等于上式右边的两项之和，所以在图5显示出，运行轨迹线点1到点2比点1到点5较平缓，前者引起的蜗壳最大水压力也远远小于后者。②9 s延时直线关闭下，运行经过点3到点4 ，以满足两种导叶关闭规律在有同样有效关闭时间的前提下，延时直线关闭的直线关闭段相比于20 s直线关闭，其关闭速度更快，机组的运行轨迹线未到达开度线的交叉严重区域6点；相反20 s直线关闭，经过点5、点6到点7，由于机组导叶的快速关闭，导致机组运行轨迹线到达开度线交叉严重区域点6。

故对比于20 s直线关闭规律，在最大水头工况下，宜采用9 s延时直线关闭规律。

图4 不同导叶关闭规律机组过渡过程计算结果对比Fig.4 Comparison results of transient progress under different closing law

工况T2：对于额定水头工况，采取不同的两种关闭规律的计算结果对比见图5。根据图5可看出：①采用简单直接的20 s直线关闭，机组转速呈现了两个波峰，如图5(a)所示，蜗壳最大水压力和最小水压力的变化幅度均大于9 s延时直线关闭，机组最大水压力尽管没有大于调保计算要求，但很接近蜗壳压力极值线，增加了机组的危险性，如图5(b)所示；②9 s延时直线关闭，机组转速变化平缓，没有出现明显的双峰性，且蜗壳最大水压力远远低于蜗壳压力极值。产生上述变化，主要是因为两种关闭规律下，流量的变化有明显的区别，由图5(a)可得，在9 s延时直线关闭规律下，因为导叶的延时拒动，机组流量变化平缓，流量未出现较大的负，并且没有出现明显的双峰性。综上所述，机组在额定水头工况下，采取9 s延时直线关闭规律比较合理。

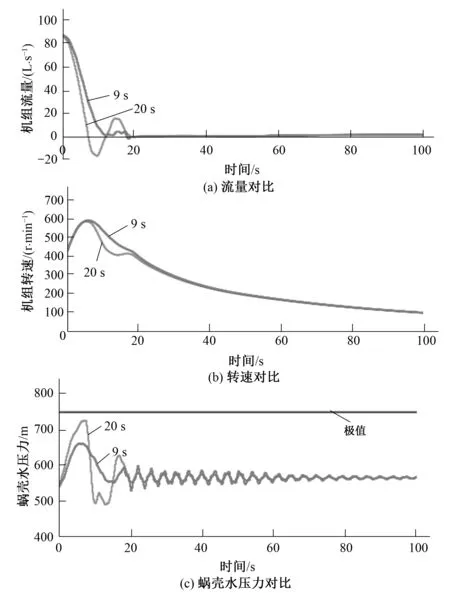
图5 不同关闭规律过渡过程计算结果对比Fig.5 Comparison results of transient progress under different closing law

工况T3：对T3工况应用两种导叶关闭规律的主要结果对比如表4所示。在满足两种导叶关闭规律有一样的导叶有效关闭时间的前提下，从表4来看：①尾水管进口最小压力在两种关闭规律下分别为77.14和79.81 m，距离调保计算要求12.10 m都有很大的安全裕度，机组转速升高相近；两种规律甩负荷过程蜗壳最大水压力对比见图5(c)。由图5(c)可看出：20 s直线关闭的蜗壳最大水压力远远小于调保计算的要求极值748.80 m。考虑到关闭规律在满足调节保证计算极值的情况下，应尽可能的简单，综上所述，对于最小水头工况宜采取20 s直线关闭规律。

表4 工况T3不同导叶关闭规律及其优化计算结果对比Tab.4 Comparison results of different closing law in conditional T3

4 结 语

针对抽水蓄能可逆式机组，工况运行水头变化跨度较大，相比于传统的导叶关闭规律优化选择，本文利用现代微机调速器的强大性能，进行水头的实时采集，实现自适应水头，同一个电站，针对不同的运行工况，机组导叶采取不同的导叶关闭规律。经过对可逆式机组分别在最大水头、额定水头、最小水头进行甩负荷过渡过程计算。

通过理论和数值分析可知：①对于最大水头493.31 m T1工况甩负荷工况，在进行导叶关闭规律的优选时，与20 s直线关闭规律相对比，采用9 s延时直线关闭时，不单可以能在满足机组转速和尾水管进口最小压力满足抽水蓄能电站调节保证计算要求的同时，而且能使得机组蜗壳最大水压力远远低于蜗壳压力极值，故在最大水头下导叶关闭规律宜采用9 s延时直线关闭规律；②针对额定水头458.93 m T2工况进行导叶关闭规律优化时，采用20 s直线关闭规律和9 s延时直线关闭规律都可以很好地满足抽水蓄能电站甩负荷调节保证计算要求；③针对最小水头438.01 m工况T3，在进行导叶关闭规律优化时，在满足抽水蓄能可逆式机组甩负荷调节保证计算要求的前提下，以简单、有效为目的，宜采用20 s直线关闭规律。

综上所述：当可逆式机组水头低于最大水头且大于额定水头时，宜采用延时直线关闭规律；当水头低于额定水头时，宜采用简单20 s直线关闭规律，可有效改善蜗壳与尾水管压力，降低机组甩负荷时的运行风险。

□

参考文献：

[1] Zheng Taoping，Tian Ziqin，Gui Shaobo，et al. Hydraulic transient process research technologyand engineering application on the complex water tunnel conveyance system of hydropower station[C]∥ Isfmfe-international Symposium on Fluid Machinery and Fluid Engineering, 2014.

[2] 王 丹, 杨建东. 导叶关闭规律及初始开度对蜗壳动水压力的影响[J]. 水电能源科学, 2005,(4):73-75.

[3] D M Bucur,C M Ghergu,N O Tanase,E C Isboiu.Transitory flow in a complex hydroelectric scheme with multiple intakes and water tanks[C]∥25th IAHR Symposium on Hydraulic Machinery and Systems, 2010．

[4] 刘晓丽, 郑 源, 高亚楠. 抽水蓄能电站可逆机组导叶关闭规律探析[J]. 水电能源科学, 2011，29(6):151-153.

[5] 陈 丹, 杨建东. 导叶关闭规律和尾水调压室对尾水管真空度的影响[J]. 水电能源科学, 2004，22(2):45-48.

[6] 李小芹, 常近时, 李长胜. 改善水轮机过渡过程品质的导叶异步关闭方式[J]. 水力发电学报, 2014，33(1):202-206.

[7] 王炳豹, 杨建东, 张新春, 等. 抽水蓄能电站上游调压室最高涌浪控制工况研究[J]. 水力发电学报, 2015，34(5):66-71.

[8] 邓鹏程, 李文明. 挂治水电厂调速器水头采集及控制功能的实现[J]. 水电自动化与大坝监测, 2011,(5):21-23.

[9] 黄贤荣. 水电站过渡过程计算中的若干问题研究[D]. 南京：河海大学, 2006.

[10] Zhao Weiguo, Wang Liying, Zhai Ziyong, et al. Application of multi-objective optimized methods in the closing law of guide vanes[J]. Chinese Corotrol & Decision Conference,2010,33(2):3 552-3 556.

[11] 芦 月. 抽水蓄能电站不同水头下导叶关闭规律研究[J]. 水力发电, 2016,42(12):85-89.

[12] 樊红刚, 崔赫辰, 陈乃祥. 导叶关闭规律非线性评价函数及多工况优化[J]. 排灌机械工程学报, 2013,(3):230-235.

[13] 鄂学全, 王 平. 特征线法分析长距离输油管道的流动瞬变过程[J]. 水动力学研究与进展, 1998, 13(4):430-440.

[14] 郑 源, 张 健. 水力机组过渡过程[M]. 北京: 北京大学出版社, 2008.

[15] 于桂亮, 蔡付林, 周建旭. 导叶关闭规律对抽水蓄能电站过渡过程的影响[J]. 中国农村水利水电, 2016,(5):189-192.