断面形态对支流分流比的影响研究

邹 健，李 涛，曲少军，王 玮

(1.华北水利水电大学水利学院，郑州 450045；2.黄河水利科学研究院黄河小浪底研究中心，郑州 450003；3.武汉大学水资源与水沙科学国家重点实验室，武汉 430072；4.黄河小浪底旅游开发有限公司，河南 洛阳 471141)

河道直角分流是一种常见的水流现象。早期，Taylor[1]、Law[2]、Ramamurthy[3]等通过水槽试验研究水流分流，研究内容多为分汊口处水流结构、回流特征和能量损失等。A S Ramamurthy等[4]和Jian-chun Huang等[5]采用数学模型研究了干支流夹角为90°时的分流区流场结构。罗福安等[6]对分水口三维流场进行了研究，分析了分水宽度沿水深的变化规律，但其理论不适用于较大的分流比情况。曹继文[7]通过水槽试验研究了横向直角取水口的水力特性。谷攀[8]采用数学模型与物理模型试验相结合的方法，以取水口附近水域流场为研究对象，研究了弯道取水口的水力特性。

对于分流比的研究，韩其为等[9]引入和项系数和当量水深作为相对引水深，同时提出了在分流前干流断面上引水面的形态，从而建立了相对引水深与分流比的关系。常宏兴等[10]结合曹继文[7]关于明渠岸边横向取水的水槽试验成果，运用数学模型模拟分汊河道不同分流比工况下的水流运动，得出了分汊河道不同分流比工况下的流速分布以及水流特性等结果。郭维东[11,12]探究了分流比变化以及取水角度变化对引水口水流流场的影响。

前人在研究明渠分流时均是干流断面形态固定，没有研究不同干流断面形态的水流分流运动特性。本文通过运用Mike21数值模拟手段，模拟1～10 L/s流量，3种断面形态下的水流运动，研究其在不同进口流量下的分流比以及分水口处的回流区，得到了一些基本认识。

1 模拟概况

本文运用Mike21水动力模块搭建不同断面形态的分流水槽的数学模型，主槽断面形态分为3种，分别是矩形、梯形、三角形，支槽为矩形断面。对于主槽3种断面形态，边坡与水平面的夹角(边坡角)为α，定义边坡系数：m=cotα，则，矩形断面边坡系数为0，梯形断面边坡系数为1，三角形断面边坡系数为2，如图1所示。

1.1 网格剖分

模型主槽为30 m×0.6 m，支槽为7.2 m×0.3 m，将主槽边坡挖空，与之平底相接。模型比降均为1%。主槽采用四边形网格0.1 m×0.05 m，在分水口处网格进行局部加密，改为0.05 m×0.05 m。支槽采用三角形网格[13]，如图2所示。

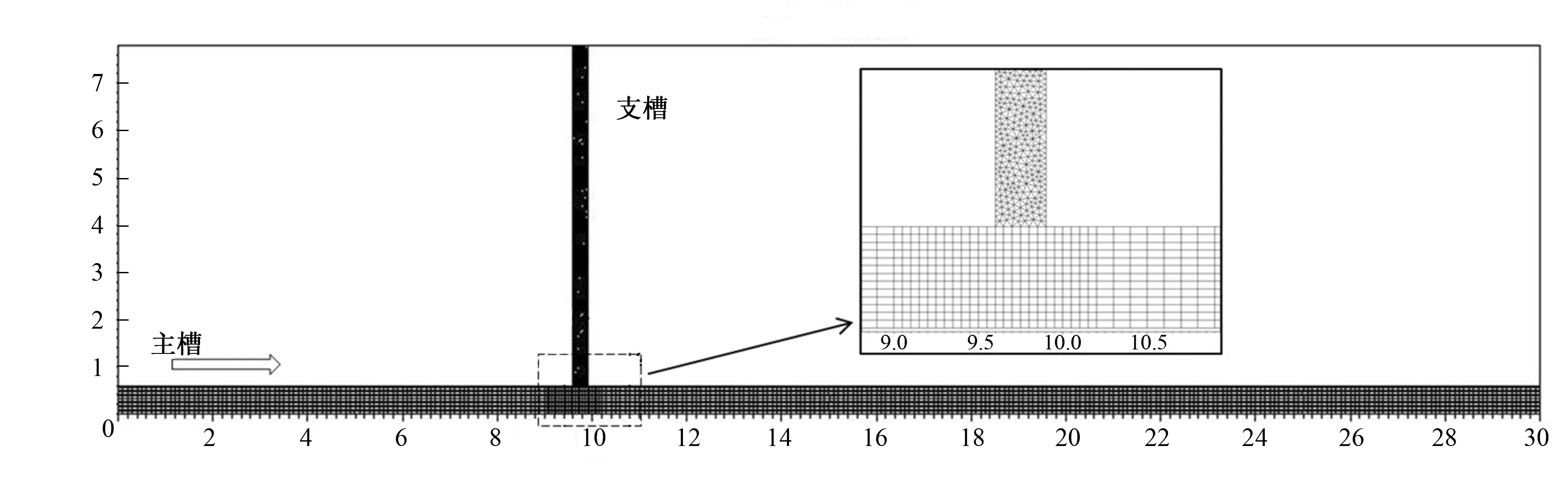
图2 网格剖分(单位：m)Fig.2 Meshing

1.2 模型验证

对该模型进行验证，试验在如图3所示的π型玻璃水槽中开展，并配备电磁流速仪进行试验。根据物理模型试验结果，对梯形断面的数学模型计算结果进行验证。将模型计算结果与试验结果对比，见图4。取5 L/s以及10 L/s两个进口流量，进行计算结果与试验结果的比较。选取干流同一断面，断面上选取7个点直接读取其流速。由图4可看出，所选取断面上流速计算值与试验值比较，两者吻合较好，验证了数学模型的可靠性，加强了模型计算结果的可信性。

图3 水 槽Fig.3 Water channel

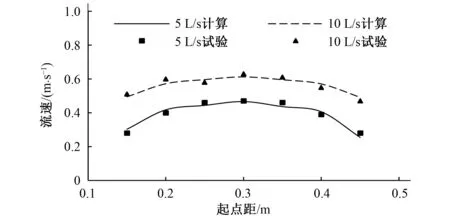
图4 计算值与试验值比较Fig.4 Comparison of simulating and experimenting value

2 计算结果分析

2.1 水力半径

水力半径是反映水流横断面几何特征和水流阻力的综合指标：

(1)

式中：R为水力半径；A为过水断面面积；χ为湿周。

A根据模型计算的水深和图1所示断面尺寸求得，计算结果见表1。

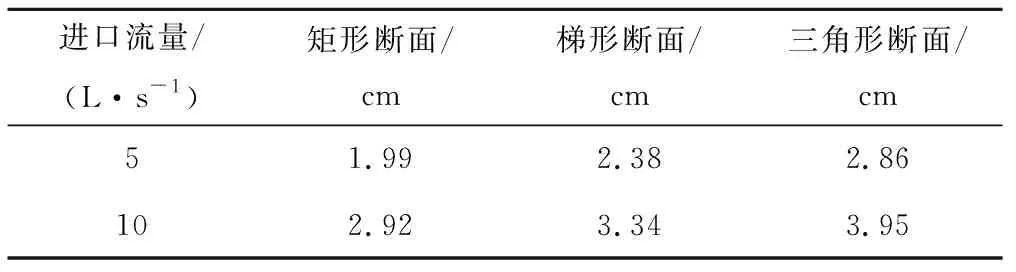
表1 不同断面形态水力半径Tab.1 Hydraulic radius of different sections

由表1可知，由于断面湿周不同，计算得到各断面形态水力半径，相同流量条件下，矩形断面的最小，三角形断面最大，梯形断面居中。

2.2 水位变化

模型出口采用自由出流控制，以进口流量5 L/s为例，不同断面下，水面线如图5所示。干流分水口上游及分水口下游水面线与水槽底坡平行，水流运动形式为明渠均匀流。

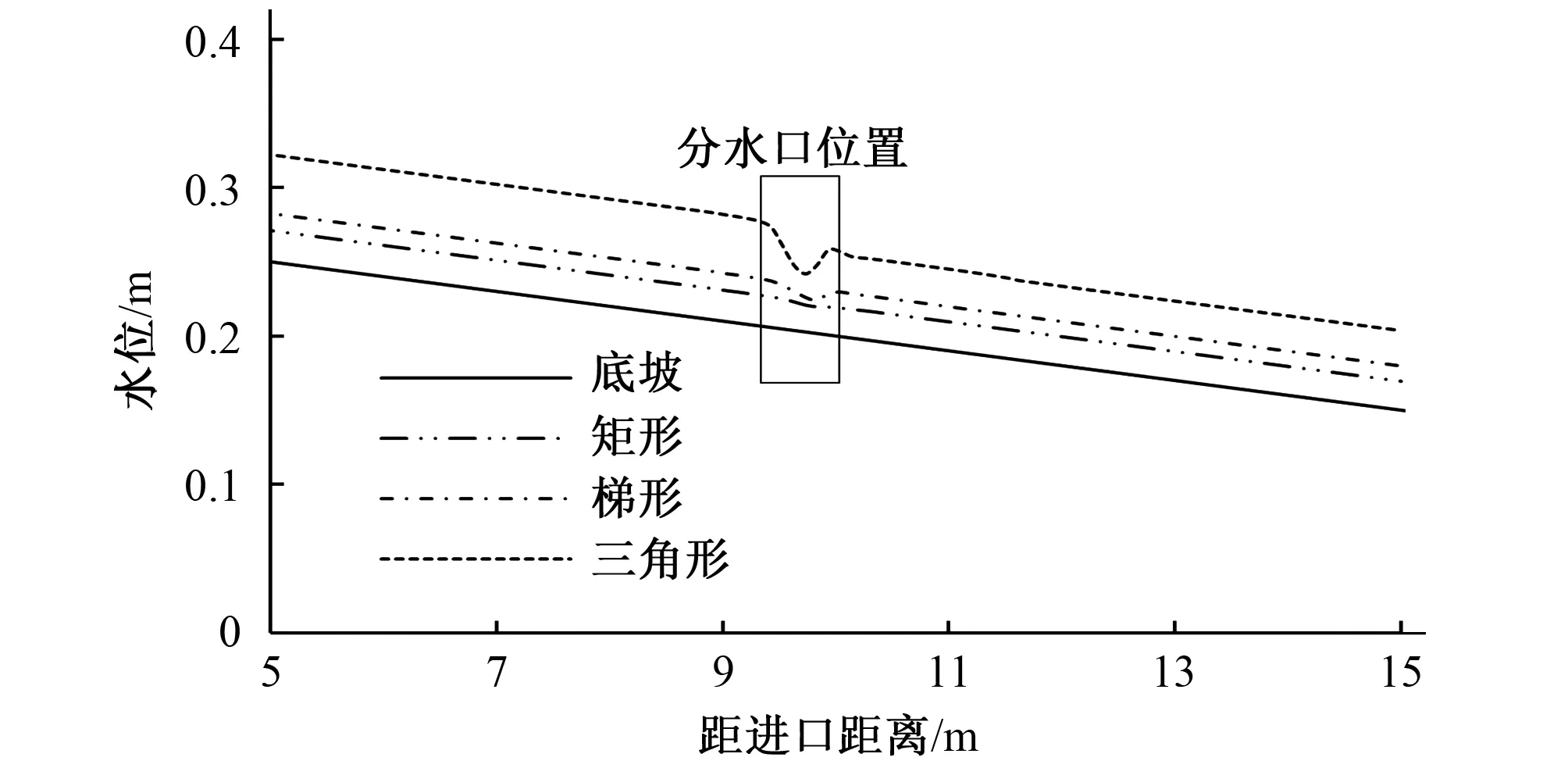
图5 沿程水位变化Fig.5 Variation of water level along the path

2.3 分流比η随边坡系数m变化

对进口流量为1、3、5、8、10 L/s的模拟结果进行汇总，并计算分流比η(支流流量与总流量比值)，结果见表2。

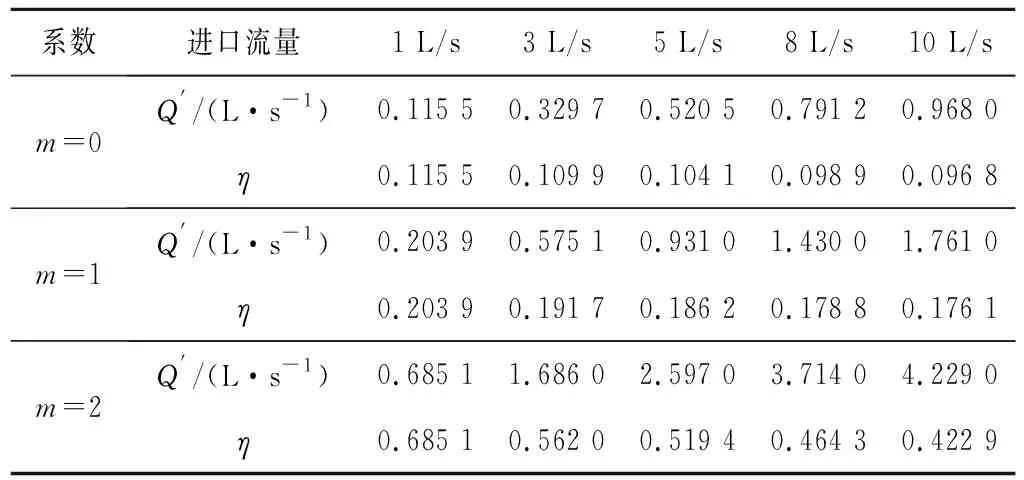
表2 不同条件下支流分流比Tab.2 Division ratio of tributaries under different conditions

不同流量下，分流比随边坡系数的变化如图6所示。由图6可知，同一流量下，边坡系数越大，支流分流越多，边坡系数在0～1之间时，分流比变化不明显，当在1～2之间时，随着边坡系数增大，分流比增加显著；随着进口流量的增加，支流分流比逐渐减小。

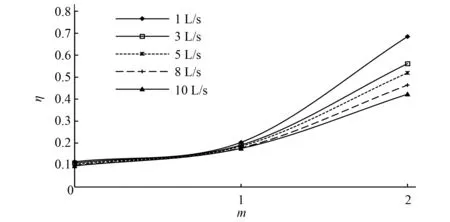
图6 分流比随边坡系数变化Fig.6 Variations in diversion ratio with side slope coefficient

2.4 分流比η随进水断面收缩系数变化

受支流取水的影响，来流流线在取水口上游一定距离处发生偏转，部分水流流入支流。在不同水流条件下，支流左岸均存在一个回流区，该回流区的强度和范围随着上游来流流量和干流边坡系数的变化而有所不同。由于回流区的影响，真正有水进入支流的宽度要比支流宽度小，有水进入支流的部分叫做有效宽度，用B来表示，如图7所示。在引水工程中，有效宽度可反映支渠引水的多少。

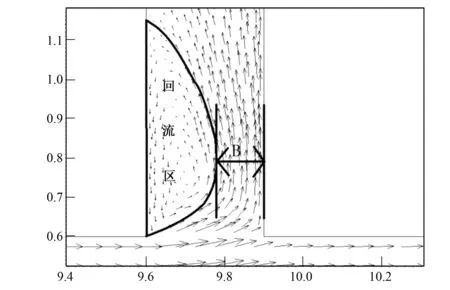
图7 支流有效宽度示意图(单位：m)Fig.7 Effective width in branch channel

选取1、3、5、8、10 L/s来作为研究对象，分别对不同边坡系数的断面形态进行模拟，得到支流引水有效宽度，将所得结果汇总为表3。由表3数据可知，同一边坡系数，随着上游来流流量的增加，使得回流区范围增大，有效宽度减小；同一流量，随着边坡系数的增大，支流内回流区范围变小，有效宽度增加。

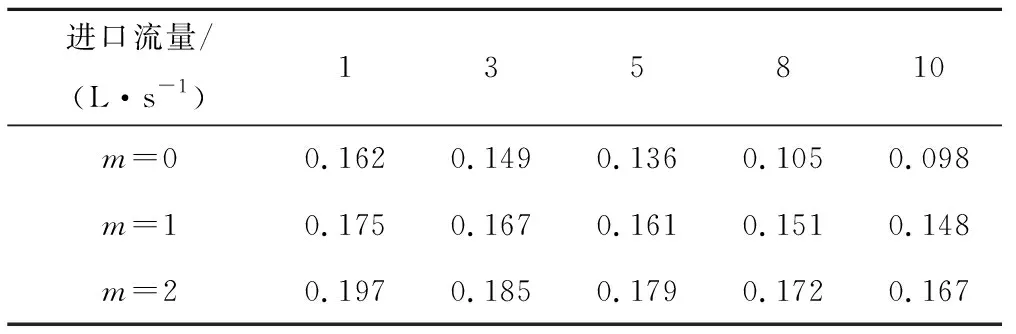
表3 支流引水有效宽度 m

回流区的存在导致支流内进流有效宽度减小，效果类似于支流进水断面宽度发生了“收缩”，因此定义进水断面收缩系数为：

δ=B/B支

(2)

式中：B为支流引水有效宽度；B支为支流宽度。

图8为分流比随进水断面收缩系数δ变化图。由图8可知，分流比随着断面收缩系数的增大而增加，且边坡系数越大，分流比随支流断面收缩系数的变化范围越大。

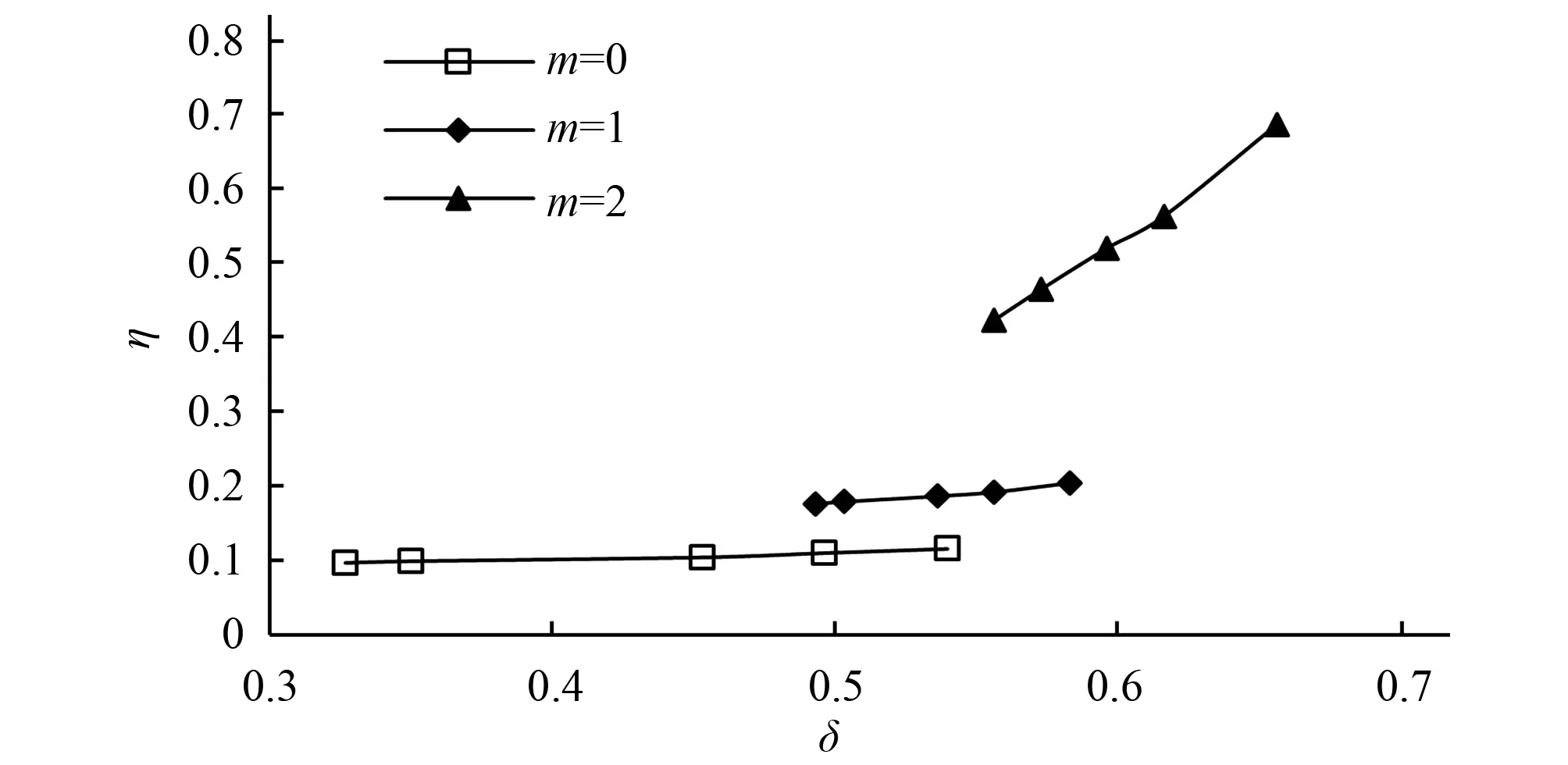
图8 分流比随断面收缩比变化Fig.8 Variations in diversion ratio with contraction coefficient

2.5 分流比η随Fr变化

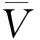
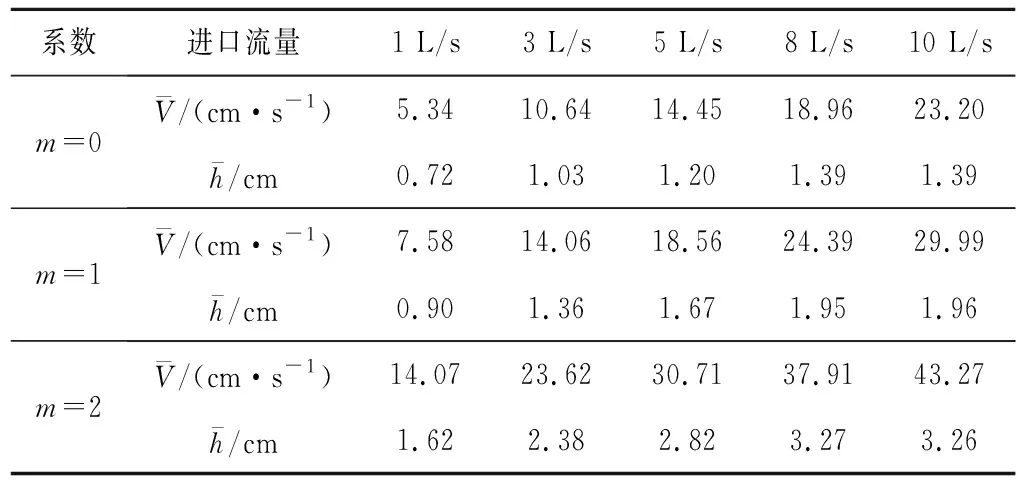
(3)

图9为3种边坡系数下，分流比η随支流水流弗劳德数Fr变化趋势。由图9可知，随着弗劳德数的增加，支流分流比逐渐减小；边坡系数越大，分流比随弗劳德数变化越明显。

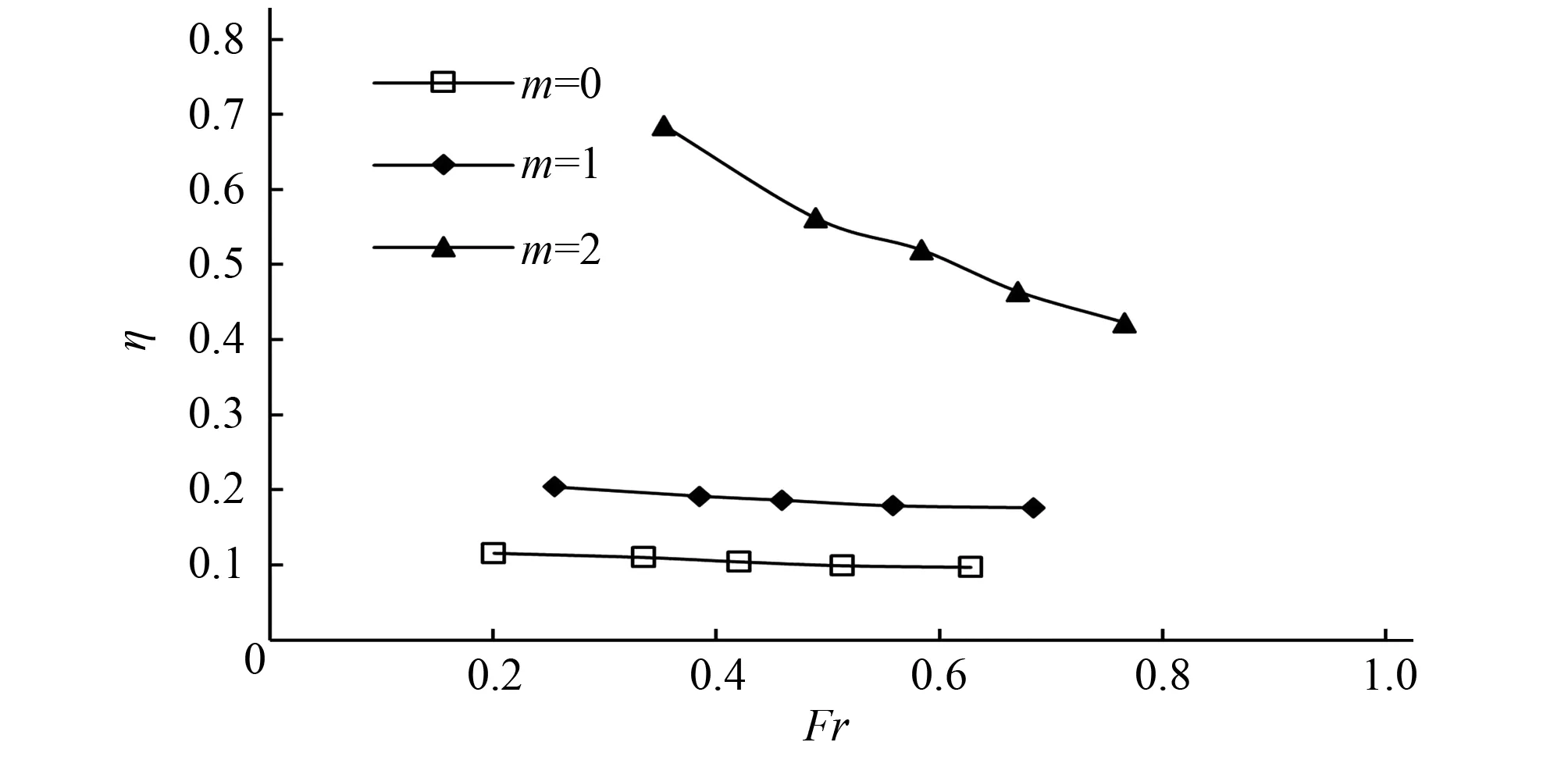
图9 分流比随弗劳德数的变化Fig.9 Variations in diversion ratio with Froude number

2.6 分流比计算

在河道分流时，为了快速准确地判断分流到各河道的流量或者分流比例，需要对分流比例及其影响因素进行定量分析。在本文中，支流断面收缩系数、弗劳德数是影响分流比的两大因素。通过数据分析软件，获得3种边坡系数下，η与δ和Fr之间的关系式：

m=0时：

η=0.109δ0.153Fr-0.093(R2=0.990)

(4)

m=1时：

η=0.198δ0.235Fr-0.113(R2=0.994)

(5)

m=2时：

η=1.681δ2.396Fr-0.104(R2=0.998)

(6)

运用拟合公式(4)～(6)计算其他流量下的分流比，计算值与实测值对比见图10。从图10可看出，计算结果与实测值较为接近。

图10 分流比计算值与实测值对比Fig.10 Comparison between the calculated and measured diversion ratio

3 讨 论

本文利用Mike21模型进行分流比的计算，考虑不同流量与边坡系数对支流分流的影响。模拟结果表明，随着上游流量的增加，有效宽度减小，分流比减小；随着边坡系数的增大，有效宽度增大，支流分流比增大。刘学军[14]对梯形主槽侧面分水进行了研究，得出了随着主槽边坡系数的增加，分流比增大的结论。景琪[15]研究对象仅为固定断面形态，没有考虑不同断面形态对分流比的变化有何影响，认为支流内回流区范围随着流量比的增大而增大，文中结合表2和图8，同样可得出此结论。说明了文中结果的可信性。

4 结 语

通过模拟不同边坡系数的干流断面，并分别给定不同的进口流量，分析结果得出：

(1)同一边坡系数下，随着进口流量的逐渐增大，支流内回流区范围增大，有效宽度逐渐减小，分流比逐渐减小。

(2)同一进口流量下，随着边坡系数的增大，支流内回流区范围减小，有效宽度逐渐增大，分流比逐渐增大。

(3)随着弗劳德数的增加，支流分流比逐渐减小，且边坡系数越大，分流比随弗劳德数变化范围越大。

(4)数据分析得到分流比与断面收缩系数、弗劳德数之间的关系式，并得到了验证。

本文仅仅研究了清水情况直角分流的特性，没有涉及泥沙问题。根据结论可知，为保证引水渠引水效率得到最大的利用，其位置选取尽量靠近断面边坡系数较大的地方。但在实际工程中，泥沙问题是不可忽视的，引水渠位置选取不仅要考虑引水量的多少，还需考虑引水过程中涉及的口门处泥沙淤积等问题，对此还需作进一步的研究。

□

参考文献：

[1] Taylor E H. Flow characteristics at rectangular open channel junctions[C]∥ Transactions of the American Society of Civil Engineers, ASCE, 109,1944:893-902.

[2] Shiu W L, Alan J Reynolds. Diversion flow in an open channel[J]. Journal of Hydraulics Division, ASCE, 1996,92(2):207-231.

[3] Amruthur S R, Duc M T, Luis B C. Division of flow in open channels[J]. Journal of Hydraulic Engineering, ASCE, 1967,24(4):393-407.

[4] Ramamurthy A S, Qu J, Vo D, et al. 3-D simulation of dividing flows in 90 deg rectangular closed conduits[J]. Journal of Fluids Engineering, 2006,128(5):1 126-1 129.

[5] Huang J, Weber L J, Lai Y G. Three-dimensional numerical study of flows in open-channel junctions[J]. Journal of Hydraulic Engineering, 2002,128(3):268-280.

[6] 罗福安, 梁志勇, 张德茹. 直角分水口水流形态的实验研究[J]. 水科学进展, 1995,6(1):71-75.

[7] 曹继文, 陈惠泉, 贺益英. 明渠岸边横向取水口水力特性的试验研究[J]. 水利学报, 2003,34(10):32-37.

[8] 谷 攀. 弯道取水口水力特性研究[D]. 呼和浩特：内蒙古农业大学, 2011.

[9] 韩其为, 何明民, 陈显维. 汊道悬移质分沙的模型[J]. 泥沙研究, 1992,(1):46-56.

[10] 常宏兴, 芦 松, 武亚辉, 等. 分汊河道分流比对河道水流流态影响分析[J]. 水科学与工程技术, 2013,(6):43-45.

[11] 郭维东, 刘 健, 韩 冬. 分流对弯道水流水力特性的影响[J]. 人民黄河, 2009,31(6):93-94.

[12] 郭维东, 张春雷, 伯彦萍, 等.分流比及取水角度对弯道引水口水流流场的影响[J]. 沈阳农业大学学报, 2017,48(2):191-199.

[13] 李 涛, 邹 健, 曲少军,等. 基于不同断面形态的直角分流口处局部损失研究[J]. 水力发电学报, 2017,36(6):30-37.

[14] 刘学军, 郑国华. 梯形主渠侧面分水研究[J]. 人民长江, 1990,(12):23-29.

[15] 景 琪, 张耀哲. 渠系分流口区域水流运动特性数值模拟[J]. 水电能源科学, 2017,(5):95-99.