基于经验频率点据的暴雨公式参数研究

吴素娟，王双银，牛 晨 (西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100)

随着社会经济的迅速发展，极端降水事件引起的城市内涝、山区洪水和泥石流等也表现出发生频率高、量级增大的特点，扰乱了人们的正常生活，严重影响了流域生态环境和区域社会的健康持续发展。短历时强暴雨是形成城市内涝和小流域洪水的最主要因素，研究短历时暴雨的统计规律，在站点逐渐增加、暴雨资料逐渐积累的基础上建立适用性强的暴雨公式，是小流域设计洪水计算的基础，可为山洪灾害防治和城市排水系统设计提供科学依据，对促进小流域水利事业发展、实现人水和谐战略、保障社会经济可持续发展具有重要的理论和现实意义[1-5]。

近几年城市内涝的频繁发生已使得暴雨公式的研究越来越受到人们的重视，从城市暴雨资料的选样到理论频率曲线的选择，再到暴雨参数的推求，关于暴雨公式的研究都取得了一定的进步与发展[6-10]。在暴雨公式研究的过程中，我国大多采用理论频率曲线，且多以P-Ⅲ型曲线作为最优分布曲线，而通过经验频率点据推求暴雨公式的研究较少，同时对于暴雨公式参数区域性规律的研究也很少[11-19]。暴雨公式的求参从原始的图解法、最小二乘法发展为基于计算机编程的各种优化算法，其中麦夸尔特法应用较多[20]。本文根据陕西省部分气象站点的实测暴雨资料，推求4参数暴雨强度公式，并结合暴雨公式参数和站点的地理位置分析了参数的地区性规律，为陕西省设计暴雨的研究提供了依据，也为陕西省无资料地区的暴雨公式参数求解提供了参考，同时为区域性城市暴雨的研究和城市内涝的防治提供了思路。

1 资料与方法

1.1 资 料

采用陕西省气象局提供的陕西省境内18个基本气象站和基准气象站1984-2013年实测暴雨资料研究暴雨公式参数，其中，秦岭以北11个测站，秦岭以南7个测站，站点的基本情况见表1。

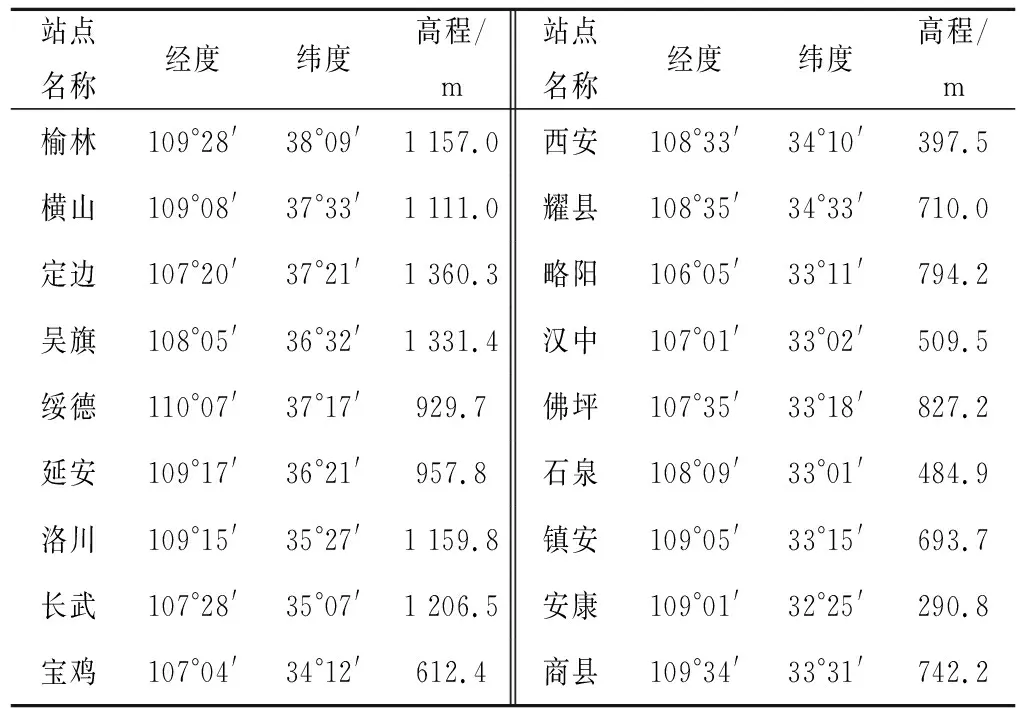
表1 陕西省主要气象台站基本情况表Tab.1 Basic situation of main meteorological stations in Shaanxi Province

1.2 研究方法

(1)选样方法。从形成小流域山洪灾害和城市内涝的暴雨特点出发，同时参照《室外排水设计规范》的要求，用年最大值选样法，取10、30、60、90和120 min 5个历时作为短历时暴雨的统计时段，对于个别缺测值直接移用邻近站点实测值。

(2)麦夸尔特法。暴雨公式的参数求解是非线性求参问题，采用的麦夸尔特法是在高斯-牛顿法的基础上引入阻尼因子后产生的一种方法，可避免求参时迭代结果无法收敛的情况，具体计算原理和过程见文献[21-23]。

2 暴雨公式形式

常用的暴雨公式有反映雨强与历时关系的两参数公式、三参数公式以及综合考虑频率、历时、暴雨强度关系的四参数暴雨公式[24]。采用文献[25]推荐的四参数暴雨公式形式如下：

(1)

式中：itp为暴雨强度，mm/min；P为频率(小数形式)；t为暴雨历时，min；A、C、b、n均为参数，其中n为暴雨衰减指数。

3 参数与精度

3.1 参数计算

通过4个不同的系列，分别用麦夸尔特法对式(1)中的参数进行求解。系列1为1984-2013年共30 a全部实测点据；系列2为1984-2013年资料中经验频率P<50%半系列中的15个经验频率点据(在设计暴雨分析计算中，通常以小频率点据为依据)；系列3为1984-2013年实测点据以P-Ⅲ型分布为理论分布，采用相对较为精确稳定的线性矩法[26]估计P-Ⅲ型分布参数后获得的与经验点据同频率的30个理论点据；系列4为系列3中的P<50%半系列中的15个理论频率点据。4个系列求得的暴雨公式参数见表2。

3.2 精度分析

根据文献[25]，暴雨公式的精度采用计算雨强与实测雨强的平均绝对均方差RMSE和平均相对均方差RSE来评定，以RMSE和RSE分别小于0.05 mm/min和5%为宜。平均绝对均方差和平均相对均方差结果见表3。

依据系列1计算的暴雨公式中除定边站RMSE=0.047 mm/min外，其他各站RMSE均大于0.05 mm/min，且全部站点的RSE均大于5%；为与P<50%半系列的误差计算保持一致，对系列1也计算了P<50%部分的RMSE和RSE，结果表明全部站点的RMSE均大于0.05 mm/min，RSE均大于5%。

依据系列2计算的暴雨公式中误差最小的站点为镇安，RMSE=0.028 mm/min，RSE=4.12%；误差最大的站点为横山，RMSE=0.065 mm/min，RSE=8.02%；有14站点的RMSE小于0.05 mm/min，占总站点数的78%，6个站点的RSE小于5%，占总站点数的33%。

依据系列3计算的暴雨公式中误差最小的站点为宝鸡，RMSE=0.053 mm/min，RSE=0.128%；误差最大的站点为耀县，RMSE=0.11 mm/min，RSE=0.227%，全部站点的RMSE均大于0.05 mm/min，RSE均大于5%。同时对系列3也计算了P<50%部分的RMSE和RSE，全部站点的RMSE和RSE均不满足精度要求。

依据系列4计算的暴雨公式中误差最小的站点也为镇安，RMSE=0.043 mm/min，RSE=5.89%；误差最大的站点是横山，RMSE=0.098 mm/min，RSE=10.91%，只有2个站点的RMSE精度达到要求，仅占总站点数的11%，所有站点的RSE均大于5%。

基于经验频率点据推求的暴雨公式平均绝对均方差和平均相对均方差均小于相同样本下基于理论频率点据求得的暴雨公式的误差。理论频率点据求暴雨公式的过程中，存在实测值与理论值的误差以及非线性求参过程中理论值与计算值之间的误差，经验频率点据与之相比就存在明显优势，避免了理论频率曲线拟合的误差。

以全系列求得的暴雨公式的平均绝对均方差和平均相对均方差大于P<50%半系列求得的暴雨公式的误差。全系列中P>50%的部分重现期小于2年，对这一部分的研究没有意义，而且会影响整体的拟合度，使得误差整体偏大；P<50%半系列中点据对应的重现期是2～30年，符合规范中的要求且拟合度更高。

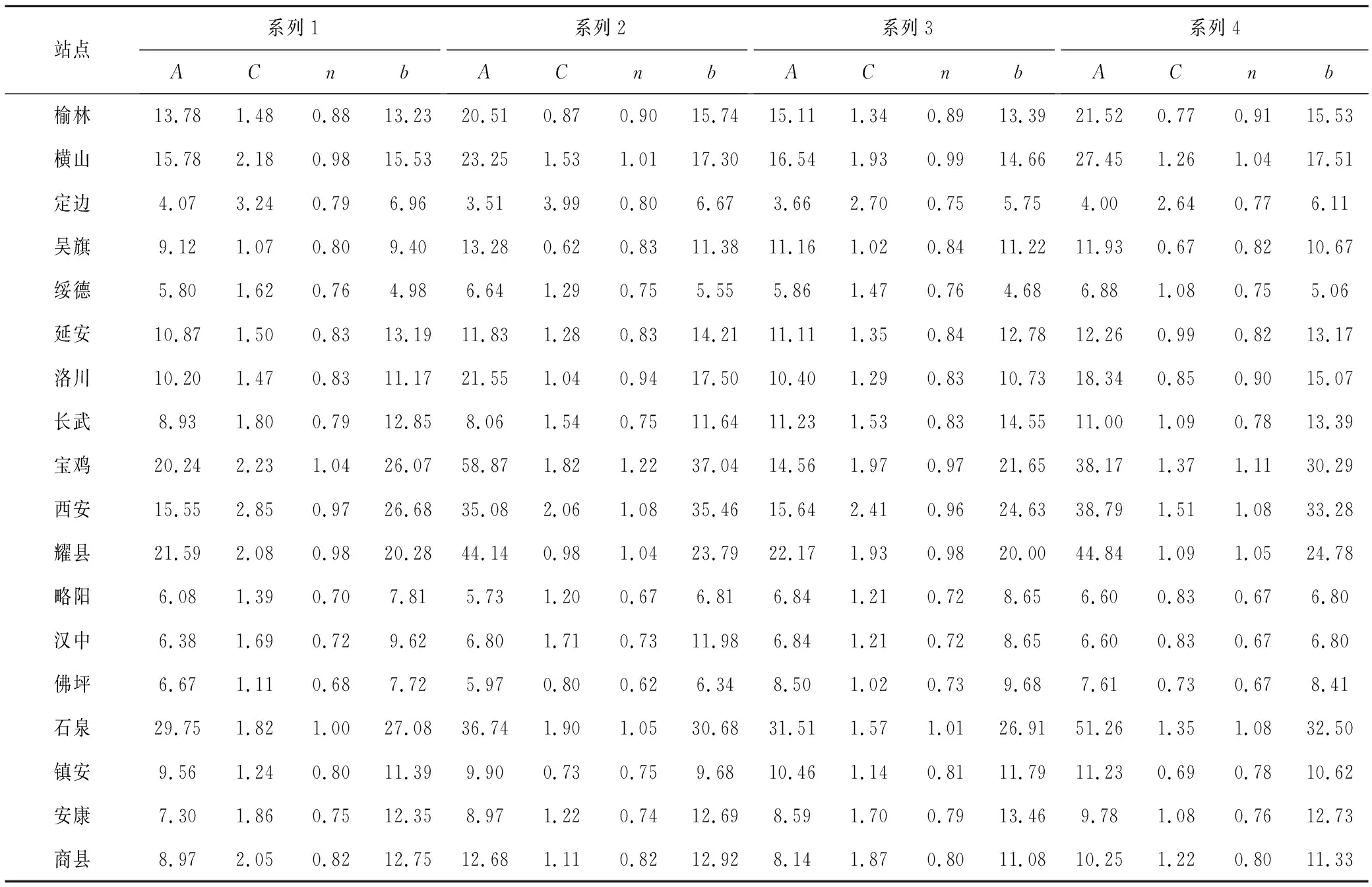
表2 陕西省主要气象站点暴雨公式参数表Tab.2 Parameters of rainstorm formula for main meteorological stations in Shaanxi Province

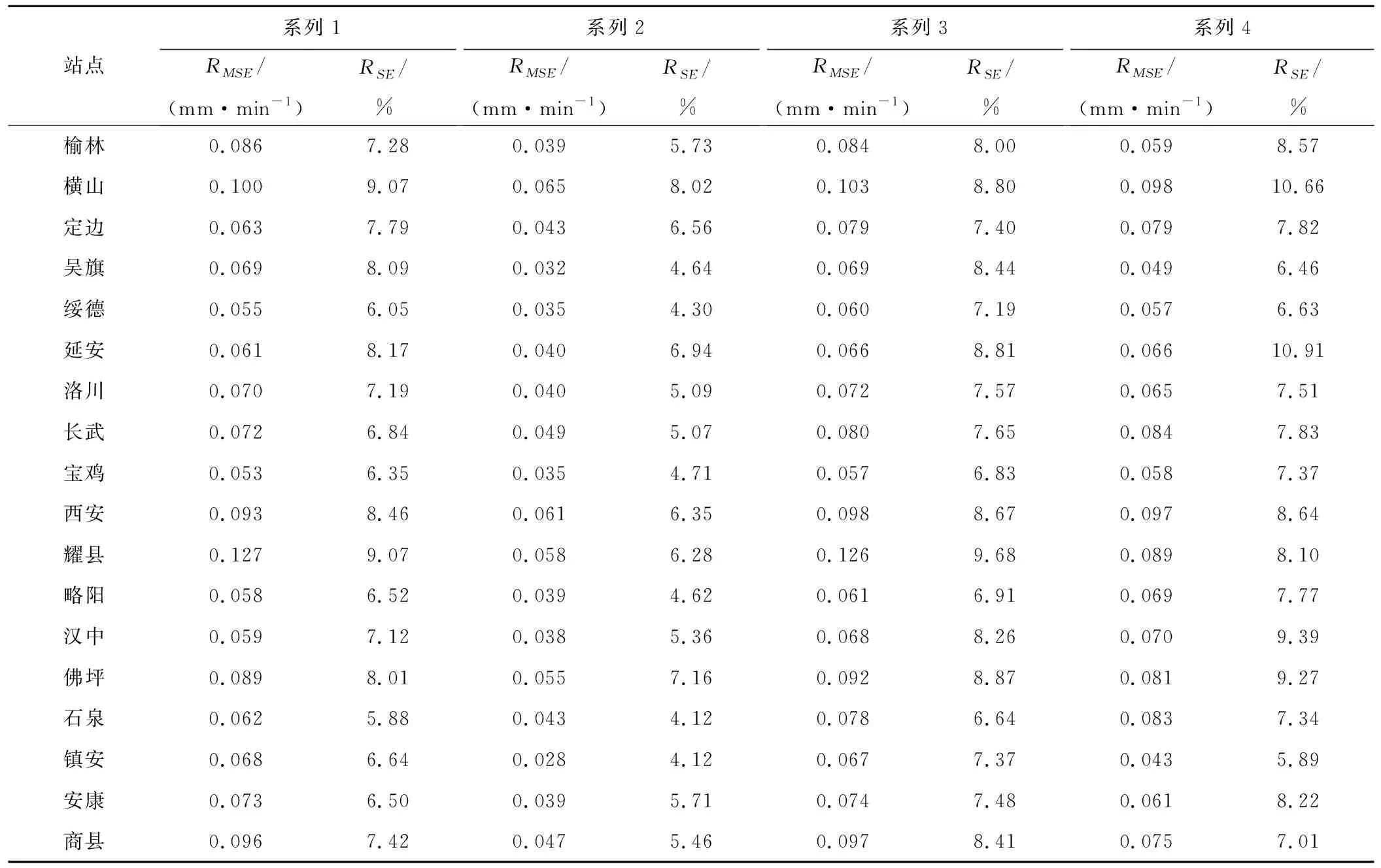
表3 陕西省主要气象站点暴雨强度公式精度计算表Tab.3 Accuracy table of the rainstorm formula for main meteorological stations in Shaanxi Province

因此，基于经验频率点据P<50%半系列(系列2)推求的暴雨公式的误差最小，且符合精度要求的站点个数最多。

在10、30、60、90、120 min这5个历时中，随着历时的增加，基于经验频率点据P<50%半系列求得的计算雨强与实测雨强之间的误差逐渐由正值变为负值，计算雨强由大于实测雨强逐渐变为小于实测雨强，这表明基于经验频率点据P<50%半系列推求的暴雨公式更适用于计算短历时暴雨强度，在较长历时下计算的暴雨强度偏小，以此为依据设计的排水工程不安全。

4 参数的区域性规律

以经验频率点据P<50%半系列推求的暴雨公式参数为研究对象，选取反映站点地理位置特征的经度、纬度和高程(分别用x、y、z表示)，与参数分别进行单因子、双因子和三因子的相关分析，同时以显著性水平为0.1的临界相关系数[27]为依据判断其相关关系是否显著。

4.1 单因子相关分析

在全区域内分析参数与经度、纬度、高程的单因子相关性，同时按秦岭以北和秦岭以南进行相关分析，分区时的相关系数与全区相比有显著提高，这表明参数有明显的分区特征。

A、n、b在秦岭以北和秦岭以南与高程的相关系数最高，相关图见图1，这3个参数在秦岭以北与高程的相关性好于秦岭以南，相关系数分别为为0.747，0.71、0.83。C在秦岭以北与经度的相关性最好，相关系数为0.503，在秦岭以南与高程的相关性最好，相关系数为0.558。

以临界相关系数检验时，全区域内只有b与高程的相关系数大于临界相关系数，在秦岭以北A、n、b与纬度和高程的相关系数通过检验，而在秦岭以南4个参数的单因子相关系数均没有通过检验。

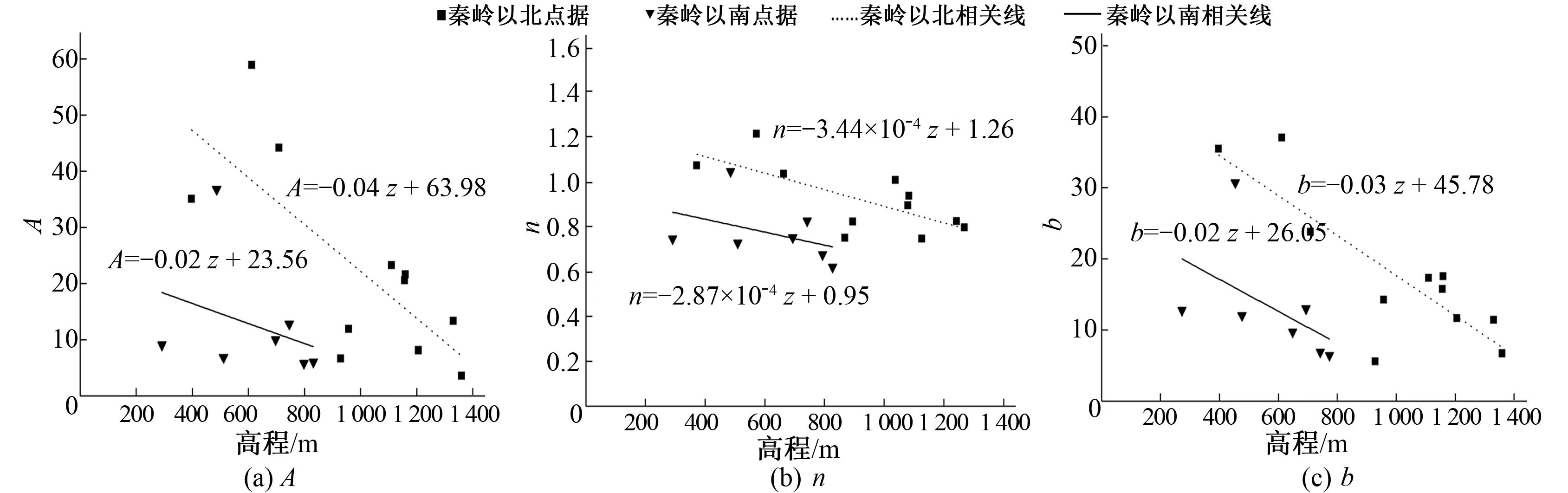
图1 A、n、b值与高程的相关图Fig.1 The correlation chart between A、n、b and elevation

单因子相关分析中，暴雨公式参数A、n、b主要受高程影响，在秦岭以北这种影响尤其明显；参数C在秦岭以北受经度的影响最大，在秦岭以南主要影响因子是高程。且在秦岭以北A、n、b与纬度和高程均存在显著的线性相关。

4.2 双因子相关分析

参数与经度、纬度、高程中的任意两个因子做三变量线性相关分析时，相关系数较单因子时有所提高。秦岭以北，A、n、b与经度、高程的双因子相关性最好，其中b的相关系数高达0.884，C受经度、纬度的综合影响最大，相关系数为0.588。A、b的双因子相关系数均大于临界相关系数，C仅与经度、纬度的相关系数超过了临界相关系数，n与经度和高程、纬度和高程的相关系数大于临界相关系数。

秦岭以南，A、n、b与纬度、高程的双因子相关系数最大，其中n的相关系数最高为0.748，C受经度、高程的影响最大，相关系数为0.706。A、C、n、b4个参数的双因子相关系数均小于临界相关系数。

双因子相关分析中，秦岭以北A、b与任意两个因子均存在显著的线性相关，C与经度、纬度相关性显著，n与经度和高程、纬度和高程有显著的线性相关，而在秦岭以南参数与双因子的相关关系均不显著。

4.3 三因子相关分析

无论是否分区，参数与经度、纬度、高程3个因子综合分析时相关系数都是最高的，双因子相关系数次之，单因子相关系数最小，计算得到的三因子综合回归方程和相关系数见表4。

全区域的相关系数小于对应分区的相关系数，秦岭以北的相关系数均大于0.6，b的相关系数最大为0.886，秦岭以南的相关系数均大于0.5，C的相关系数最高为0.944。秦岭以北的相关系数整体优于秦岭以南。在全区域和秦岭以北，相关系数均大于临界相关系数，而在秦岭以南所有参数的三因子相关系数均达不到显著性检验。

A、n、b与纬度、高程的双因子相关系数和三因子相关系数相差不大，增加的经度这一因子对它们的影响很小，其主要影响因子是纬度和高程；C在秦岭以南的主要影响因子是高程，而在秦岭以北，经度是主要影响因子，高程对它的影响相对较小。

按秦岭以北和秦岭以南分区分析时，A、C、n、b与地理位置的单因子、双因子和三因子相关系数均好于全区域整体分析的相关性。在研究暴雨公式参数的区域性规律时，要根据研究区域的实际情况，考虑是否分区进行分析。

表4 暴雨公式参数与经度、纬度、高程关系表Tab.4 Correlation between rainstorm formula parameters and latitude, longitude, elevation

注：经度、纬度和高程分别用x、y、z表示。

A、C、n、b4个参数与经度、纬度和高程的相关关系中，纬度、高程是参数A、n、b的主要影响因子，经度对它们的影响较小；C在秦岭以北与经度相关性最好，基本不受纬度和高程的影响，而在秦岭以南与高程的相关性最好，受经度、纬度的影响较小。秦岭以北，参数与经度、纬度、高程的三因子综合相关系数最高，且均通过了显著性检验，回归方程基本可以反映其变化规律，可应用于实际工作中。秦岭以南仅有7个站点，虽然参数的三因子相关系数较高，但均未通过显著性检验，不能真实地反映参数地区性规律。受站点数量的限制，参数与地理位置的具体相关关系有待进一步深入研究。

5 结 语

(1)基于经验频率点据推求暴雨公式与应用P-Ⅲ型理论频率曲线推求暴雨公式相比，存在明显优势。经验频率点据求得的暴雨公式精度更高，并且推求的过程也更简洁高效。

(2)分别以全系列和P<50%半系列的资料求得的暴雨公式中，P<50%半系列推求的暴雨公式在计算P<50%频率下的暴雨强度时误差更小。

(3)以4组系列推求暴雨公式，基于经验频率点据P<50%半系列求得的暴雨公式精度最高适用性最好，以此为依据设计的工程更安全可靠。

(4)暴雨强度公式4个参数均与地理位置存在一定的相关性，在秦岭以北与三因子存在显著线性相关，回归方程基本可以反映参数区域性变化规律。

□

参考文献：

[1] Sun Q, Miao C, Qiao Y, et al. The nonstationary impact of local temperature changes and ENSO on extreme precipitation at the global scale[J]. Climate Dynamics, 2017,49(11-12):4 281-4 292.

[2] Li YU, Ying XU, Zhang Y, et al. Temporal and spatial variation of rainstorms and the impact of flood disasters due to rainstorms in China in the past 25 years[J]. Torrential Rain & Disasters, 2018，37(1)：67-72.

[3] 张 炜,李思敏,时真男. 我国城市暴雨内涝的成因及其应对策略[J]. 自然灾害学报, 2012,(5):180-184.

[4] 邵尧明,邵丹娜,马锦生. 城市新一代暴雨强度公式编制实践及建议[J]. 中国给水排水, 2012,28(8):26-29.

[5] 陶 云,唐 川. 人类活动和降水变化对滑坡泥石流中长期演变的影响[J]. 高原气象, 2012,31(5):1 454-1 460.

[6] 邓培德. 城市暴雨两种选样方法的概率关系与应用评述[J]. 给水排水, 2006,32(6):39-42.

[7] 班 超,叶兴成,王 飞,等. 控制暴雨公式参数精度的综合误差法[J]. 中国农村水利水电, 2017,(8):62-64,69.

[8] 程 昶,周玉良,陈 雰,等. 安庆市短历时暴雨强度公式推求[J]. 水电能源科学, 2015,(7):1-6.

[9] 庄智福,王珂清,杨 杰,等. 镇江市新一代暴雨强度公式研制及雨型设计[J].气象科学, 2015,35(4):506-513.

[10] 顾春新. 城市短历时暴雨强度公式及参数确定方法研究[D]. 南京: 河海大学, 2007:4-6.

[11] 张子贤,孙光东,韩成标,等. 暴雨衰减指数为函数型的暴雨强度公式确定方法[J]. 给水排水, 2012,38(7):127-130.

[12] 中国市政工程西北设计研究院有限公司. 给水排水设计手册(第五册)[M]. 2版. 北京:中国建筑工业出版社, 2014.

[13] 邓培德. 城市暴雨两种选样方法的概率关系与应用评述[J]. 给水排水, 2006,32(6):39-42.

[14] 戴有学,王振华,戴临栋,等.山西临汾市城区暴雨强度公式修订分析研究[J].自然灾害学报报,2017,(6):197-206.

[15] 邵尧明. 最大值选样配合指数分布曲线推求雨强公式[J]. 中国给水排水,2003,19(z1):142-144.

[16] 周玉文,翁窈瑶,张晓昕,等. 应用年最大值法推求城市暴雨强度公式的研究[J]. 给水排水, 2011,37(10):40-44.

[17] 金光炎. 城市设计暴雨频率曲线线型的研究[J]. 水文, 2002, 22(1): 20-22.

[18] 张子贤,孙光东,孙建印,等. 城市暴雨强度公式拟合方法研究[J]. 水利学报, 2013,44(11):1 263-1 271.

[19] 夏宗尧. 编制暴雨强度公式中应用P-Ⅲ曲线与指数曲线的比较[J]. 中国给水排水, 1990,(3):32-38.

[20] 任伯帜,许仕荣. 基于Marqardt-Hartley法及其在求解城市暴雨强度公式参数中的应用研究[J]. 湖南大学学报(自然科学版), 2002,29(3):96-100.

[21] 李树平，刘遂庆，黄廷林. 用麦夸尔特法推求暴雨强度公式参数[J]. 给水排水, 1999,(2):26-29.

[22] 卢崇飞, 高惠璇, 叶文虎. 环境数理统计学应用及程序[M]. 北京:高等教育出版社, 1988.

[23] 袁亚湘,孙文瑜. 最优化理论与方法[M]. 北京:科学出版社, 1997.

[24] 陈正洪，王海军，张小丽. 深圳市新一代暴雨强度公式的研制[J]. 自然灾害学报, 2007,16(3):29-34.

[25] GB50014-2006,室外排水设计规范[S].

[26] 梁玉音,刘曙光,钟桂辉,等.线性矩法与常规矩法对太湖流域降雨频率分析的比较研究[J].水文, 2013,33(4):16-21.

[27] 陈彦光.地理数学方法[M]. 北京:科学出版社, 2011.