基于模拟退火人工鱼群混合算法确定含水层参数

谭 璟，张永祥，张大胜

(北京工业大学建筑工程学院，北京 100124)

导水系数、储水系数等水文地质参数的确定对地质工程设计、地下水数值模拟、评价具有重要的意义。目前，通过地质钻探测量或者利用抽水试验是获取水文地质参数的主要途径。确定含水层参数时，采用的抽水试验的方法又可分两类，一类是以稳定抽水试验[1]采用的裘布依公式计算。另一类是以非稳定抽水试验[2,3]，采用如图解法、配线法等来确定，它是目前确定水文地质参数的主要方法。近年来，随着智能优化算法的发展，如遗传算法[4,5]、粒子群优化算法[6]、模拟退火(SA)算法[7]等也可应用于含水层参数的确定。多数人工智能算法的反演虽然便利、快捷，但单一的智能算法在解决实际应用时因为算法的不足影响计算结果和工作效率，例如：遗传算法[8]存在编码不规范等问题，粒子群算法[9]易于陷入局部最优解等。本文依据人工鱼群和模拟退火两种算法各自的特点，将两种算法混合并应用在地下水模型参数反演中。

1 模拟退火人工鱼群混合算法

1.1 人工鱼群与模拟退火算法

人工鱼群(AF)算法是中国学者李晓磊[10]等2002年首先提出的一种模拟鱼群行为的新型智能优化算法，此算法优点是：对初始值要求不高、计算迅速、参数的设定允许有较大的容许范围等。AF算法的中心策略是在求解最优化问题时，在定义域内不同点对应着不同的食物含量，食物含量最多的区域代表求解问题的最优解，然后各条人工鱼分别模仿鱼的觅食、聚群、追尾、跟随4种行为，不同的行为相互进行比较，并选择食物含量最多的一种行为进行操作，再用公告牌记录食物最高的点和食物浓度值，通过这样的寻优方式，实现最优化求解。AF算法通过设定的参数寻优时，虽然具有良好的全局收敛性，但接近最优解时，步长和视野往往制约人工鱼的行动，计算结果在最优值附近来回振荡，难以提高结果精度。

SA算法[11]的原理是将固体加热至充分高，使固体内部粒子无规律运动，再通过降温使其变得有序，不同的温度都存在一个平衡态，最终在常温时，内能减为最小。在较小的范围内，SA算法的寻优速度快、收敛精度高，利用粒子不断降低内能的方式实现最优化求解。SA算法具有在较小的范围内，它的寻优速度快、收敛精度高等特点，但是寻优的结果受初始值的影响较大。

1.2 模拟退火人工鱼群(SAAF)混合算法的实现

根据文献[12]给出的人工鱼4种行为描述公式，对AF算法的缺陷进行深入分析后发现，假设AF算法的步长和视野设定为一个固定的常数，如果参数设置较大，AF算法虽可快速收敛到最值点附近，却难以继续向最值点靠近；如果参数设置较小，还未到达最值所在区域就已经结束计算了。本文提出了AF算法与SA算法结合的混合优化算法求解最优化问题，该算法设计思路为：先利用AF算法对目标函数进行优化，迭代一定次数后，输出当前最优值，接着把AF算法的当前最优解作为SA算法的初始值，继续寻找最优解。SAAF混合算法优化时，前期利用AF算法全局性的优点找到最优值区域，后期利用SA算法良好的局部搜索能力进行局部优化，获得最优值。两种算法的混合过程简单、易实现，只需将AF算法的输出结果作为SA算法的初始值即可。

SAAF混合算法的寻优步骤为：①给出两种算法必要的基本参数，如鱼群总数N、单条人工鱼尝试的最大次数Number、初始温度T0、降温系数等；②在定义域的范围内随机生成N条人工鱼；③计算鱼群个体间各条人工鱼的目标函数值，用公告牌记录下当前最优值；④每条人工鱼模拟4种行为，不同的行为相互进行比较，并选择食物含量最多的一种行为进行操作；⑤人工鱼模拟一次行为后均要检验自身目标函数值与最优值，并更新公告牌；⑥迭代满足条件后，输出AF算法的最优解并作为SA的初始值；⑦执行SA算法，直到迭代满足条件。

2 目标函数

2.1 泰斯公式

均质、各向同性的条件下承压含水层， 有一口抽水井以流量Q进行稳定抽水，如果在抽水开始后边界对井不发生明显的影响情况下，经过t时刻，在距离抽水井r处的水位降深s可以表示为：

(1)

(2)

式中：u无量纲时间 ；T为含水层导水系数；S为储水系数；W(u)为泰斯井函数。

W(u)表达式为：

(3)

为了方便计算，通常W(u)将展开成级数形式，通常n取到5：

(4)

2.2 目标函数的建立

利用SAAF混合算法求解优化问题时，通过人工鱼给出S、T的值使得目标函数的值最小，即：

(5)

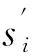
3 计算实例

3.1 原始数据

为了验证方法的可靠性，采用文献[13]中例4.1给出的原始试验资料进行数值试验。试验中的抽水稳定流量为60 m3/h，抽水时间持续1 185 min，表1给出了抽水开始后距离抽水井为140 m处有观测孔记录的降深s的观测资料，通过编程进行计算，SAAF混合算法相关参数设定如下：鱼群的规模N为20条，AF算法的迭代次数Number=50次、拥挤度因子δ=0.2、尝试次数Try_number为5、步长为3，视野为20、初始温度为50、降温系数为0.95、SA迭代次数为100、温度迭代次数为20、温度阈值为0.1，S与T的取值范围分别为(0,0.01)和(0,4 800)。

表1 抽水试验观测资料Tab.1 Pumping test data

3.2 结果分析

3.2.1 SAAF混合算法可靠性分析

表2计算出了SAAF混合算法求得的含水层参数(S为2.51×10-4，T为193.37 m2/d)、目标函数值及在不同时刻下计算水位与实测水位中最大相对误差值、平均相对误差，求解参数与文献中采用的其他方法所计算的结果数值相近，SAAF混合算法求解的目标函数值为1.19×10-3均小于表2中其他方法计算的目标函数值(范围在1.75×10-3～35.26×10-3)，最大相对误差和平均相对误差较传统方法有一定的降低。因此SAAF混合算法的计算结果更可靠、求解精度更高，把反演的参数T与S代入公式(1)后计算降深值更符合实测降深值，见图1。

表2 多种的计算结果对比Tab.2 Comparison of the variety of calculation results

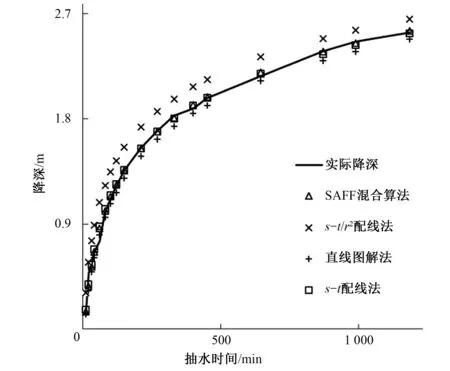
图1 多种方法的实际值与计算值的比较Fig.1 Comparison of the actual and calculated values of various methods

3.2.2 SAAF混合算法稳定性分析

表3给出了AF算法和SAAF混合算法在连续运行5次的计算结果。AF算法在运行5次过程中，人工鱼可以收敛至最优值区域，由于步长和视野的限制，使AF算法计算结果在最值点来回振荡，难以提高收敛精度，最终AF算法的目标函数值也仅有两次低于10-2；SAAF算法充分发挥了两种算法的优点，多次计算结果稳定。通过数理统计分析发现：目标函数值小于10-2的置信度为0.95条件下，AF算法至少要连续运行6次，SAAF混合算法仅需1次。

表3 连续运行5次下的AF算法与SAAF混合算法计算结果对比Tab.3 Comparison of AFSA and AAFSA of calculation results by running 5 times continuously

表4给出了AF算法与SAAF混合算法在迭代150次条件下，迭代至50次、70次、100次、150次的目标函数、导水系数、储水系数以及运行时间，AF算法在迭代132次时，函数收敛，为了获得可靠的参数需要连续运行6次，用时为25.14 s。SAAF混合算法迭代76次时收敛，见图2，用时为2.22 s，比AF算法求解含水层参数节省时间约23 s。因此SAAF混合算法不仅收敛速度更快而且运行时间更短。

表4 AF算法与SAAF混合算法计算结果对比Tab.4 Comparison of AFSA and AAFSA of calculation results

4 结 语

SAAF混合算法是SA算法和AF算法混合的随机寻优算法，它具有前期全局寻优强、后期收敛速度快、求解精度高等优点。本文先利用AF算法对初始参数不敏感、快速收敛至最值区域的特点，再将AF的当前最优值作为SA算法的初始值，SA算法利用其良好的局部搜索能力，使目标函数可以快速收敛，混合算法结合过程简单、易于实现。应用证实：

(1)通过表2所列方法求得的含水层参数代入泰斯公式求得的计算水位与实测水位相比，SAAF混合算法求解的E(S，T)为1.19×10-3，在本文对比的方法中目标函数的值最小，计算降深值也更符合实测值，因此SAAF混合算法求解的参数更符合实际水文地质工程的要求。

(2)SAAF混合算法计算的目标函数为1.19×10-3。SAAF混合算法在寻优的过程中，充分发挥了两种算法的特点，计算结果精度更高。

(3)多次运行算法时，AF算法计算结果在最优值附近来回振荡，SAAF混合算法多次运行计算结果一致；单次运行时，AF算法在迭代到第132次时，目标函数收敛，SAAF混合算法在迭代到第76次时。利用AF算法反演出较为可靠的参数需要至少运行6次，用时超过25 s，SAAF算法只要运行一次大约2.2 s，因此SAAF算法计算结果更稳定、求解含水层参数时，计算效率更高。

□

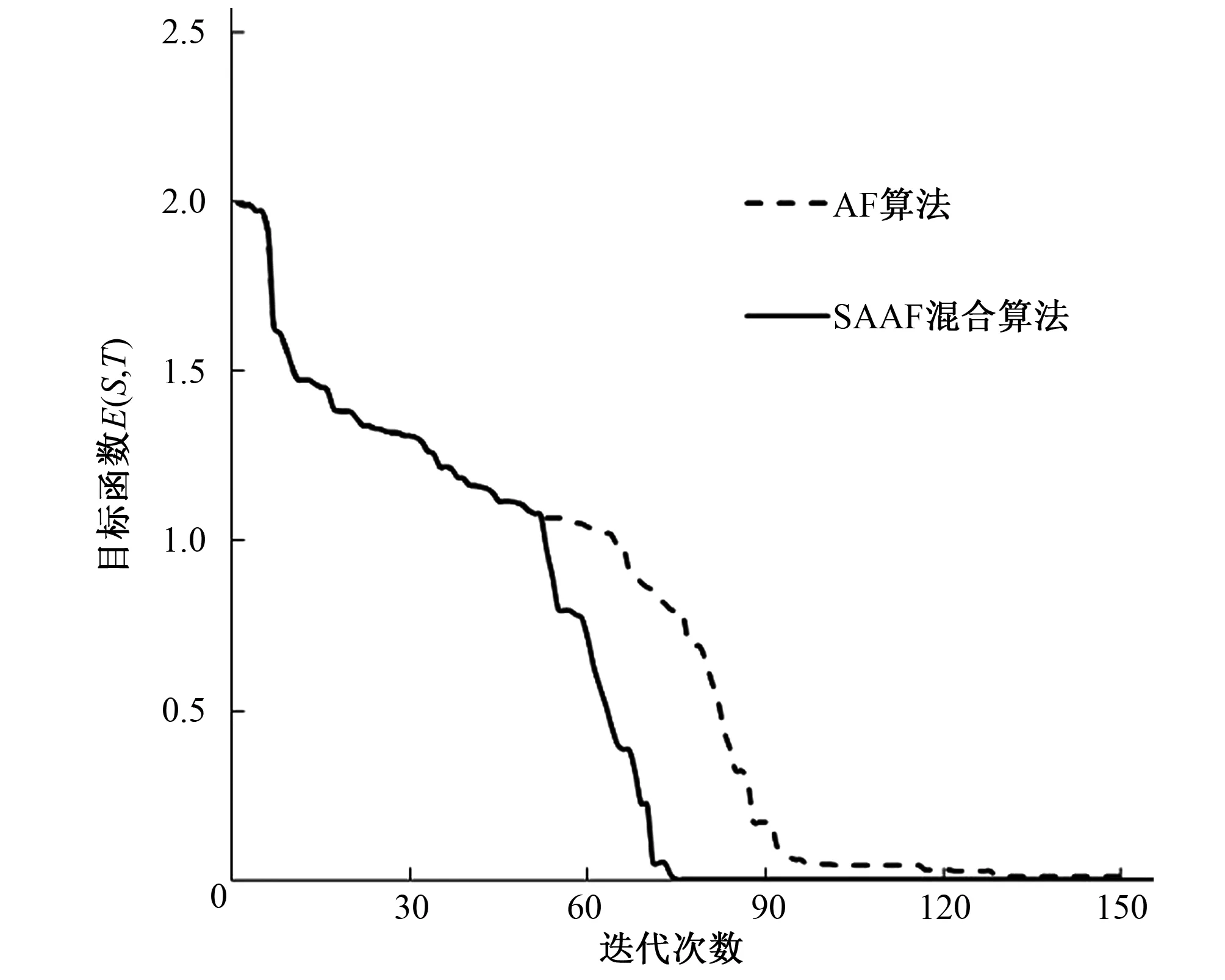
图2 目标函数的收敛曲线图Fig.2 The convergent curve of the objective function

参考文献：

[1] 万 力. 裘布依公式与泰斯公式中渗透系数间的关系[J]. 水文地质工程地质,1987,(2):61-62,56.

[2] 郭建青,周宏飞,李 彦. 分析含水层水位恢复数据的多次直线解析法[J]. 岩土力学,2008,29(12):3 246-3 250.

[3] 廖梓龙,魏永富,郭中小，等. 一种基于MATLAB的渗透系数确定方法[J]. 水资源与水工程学报,2012,23(2):175-178.

[4] 高志亮,陈 石,高 鹏. 基于遗传算法的地下水非稳定流求参方法[J]. 西安科技大学学报,2004,(4):434-437.

[5] Manoj P Samuel, Madan K Jha. Estimation of aquifer parameters from pumping test data by genetic algorithm optimization technique[J]. Journal of Irrigation and Drainage Engineering, 2003,129(5):348-359.

[6] 周秀秀,常安定,郭建青,等. 混沌粒子群优化算法在确定含水层参数中的应用[J]. 水资源与水工程学报,2013,24(1):96-99.

[7] 张娟娟,郭建青,韩淑敏,等. 基于改进模拟退火算法反演水文地质参数[J]. 中国农村水利水电,2005,(9):5-8.

[8] 雷 亮,汪同庆,彭 军,等. 改进的自适应遗传算法应用研究[J]. 计算机科学,2009,36(6):203-205,247.

[9] 袁 华,刘元会,郭建青,等. 基于改进的粒子群优化算法确定河流水质参数[J]. 西北农林科技大学学报(自然科学版),2014,42(11):220-224.

[10] 李晓磊. 一种新型的智能优化方法-人工鱼群算法[D].杭州：浙江大学,2003.

[11] 康立山. 非数值并行算法(第1册)模拟退火算法[M].北京：科学出版社,1994.

[12] 江铭炎,袁东风. 人工鱼群算法及其应用[M]. 北京：科学出版社,2012.

[13] 薛禹群,吴吉春.地下水动力学[M]. 3版. 北京：地质出版社,2010.