基于AIS实时数据的航道交通拥堵快速判定方法

何正伟， 刘力荣， 杨 帆, 王开森

(1.武汉理工大学 航运学院， 武汉 430063；2.国家水运安全工程技术研究中心， 武汉 430063;3.内河航运技术湖北省重点实验室， 武汉 430063)

随着大型船舶不断增多，航道交通拥堵问题时有发生，不仅会延误船舶航行和进出港，还会增加船舶交通事故发生的可能性。如何快速、准确地判定航道交通状态成为目前亟待解决的问题。

已有许多学者对航道和公路交通拥堵问题进行研究。刘予笑[1]分析船舶定位数据，建立航道拥堵分级指标模型，提出基于模糊综合评价的航道拥堵识别方法；刘赛龙等[2]提出航道服务水平指标和等级，将其与船舶交通流理论相结合，建立内河航道通过能力计算模型；刘明俊等[3]分析航道通过能力的影响因素，选取修正系数，建立基于船舶流的航道通过能力计算模型；祝付玲[4]借鉴国外的公路通行能力手册(Highway Capacity Manual，HCM)，建立城市道路交通拥堵评价指标体系；KNORR等[5]基于三相交通理论，提出通信检测和控制拥堵技术，使公路交通拥堵可观、可控；LAKAS等[6]基于Geocast协议，制造车对车通信系统，可有效判定公路交通状况。

当前，公路交通拥堵判定方法已较为成熟，拥有科学的判定指标体系,而航道交通拥堵判定大多基于航道通过能力来确定拥堵分级原则，属于人工判定和事后判定，缺乏实时性，海事部门难以及时处理航道交通拥堵问题。为解决该问题，本文借鉴国内外道路交通拥堵判定方法，结合交通流参数和船舶领域模型等，实时计算船舶自动识别系统(Automatic Identification System,AIS)数据，建立航道交通拥堵快速判定模型。

1 航道交通拥堵判定原则和流程

1.1 判定原则

将航道交通状态分为严重拥堵、一般拥堵和畅通等3种。严重拥堵是指航道中船舶很多，船舶时动时停或完全停滞；一般拥堵是指航道中的船舶虽然较多，但船舶尚能低速航行；畅通是指航道中的船舶不多，船舶能按正常速度航行。

国外相关研究[4]通过HCM确立V/C(交通量与通行能力的比值)、服务水平(公路运行服务质量)等公路交通拥堵评价指标。在研究航道交通拥堵时，可借鉴这些指标，并参照美国公路服务水平(见表1)和服务水平与速度的关系(见表2)。

表1 美国公路服务水平的分类

本文借鉴E等和F等服务水平。当服务水平为E等时，公路开始出现交通拥堵，车辆行驶速度比自由流速度下降约70%；当服务水平为F等时，公路严重拥堵，C/V>1。同理，航道服务水平和交通状态也遵循该规律。

1.2 判定流程

1) Spark实时数据处理平台实时接收AIS在线数据，对数据进行解析、预处理、匹配和传送等，然后自动统计数据个数m1。

2) 将经纬度为负值或大大偏离航道的数据清除掉，剩下m2个数据。

表2 服务水平与速度的关系 %

3) 船舶数据集中分布的区域才是有效的，反映航道的走向。选取合适的经纬度范围作为有效区域，有效区域内有m3个数据。

4) 多数航道是弯曲的，对整段航道进行精确计算不容易，可在其中选取某个经纬度范围内的小段航道作为研究区域，该区域内有m4个数据。

5) 对m4个数据进行分类，将MMSI相同的数据归为一类，共分成m5类，即有m5艘船。

6) 用Polynomial(多项式)函数将研究区域内的数据拟合成曲线1，清除偏离主航道的数据，剩下m6个数据，再用Polynomial将其拟合成曲线2，曲线2可视为该段航道的主航道。

7) 在曲线2上取(x1,y1)和(x2,y2)这2点作为该段航道的主航道起止点，用经纬度坐标计算两点间的距离，求出其长度s0。

8) 从步骤“5)”中已分类的数据中找出各船船长，结合s0和标准船舶艘次求出航道实际密度ρ1。

9) 将各船船长和标准船舶艘次结合起来，借助船舶领域模型求出航道阻塞密度ρ0。

11) 确定航道自由流速度u0。

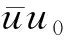
1.3 Spark实时数据处理平台

由于普通数据处理软件难以快速处理大量AIS数据，故采用Spark实时数据处理平台。Spark是一种可处理大数据集合的低延迟集群分布式计算系统。[7-8]

首先运用Spark实时接收并解析AIS在线数据，对数据进行格式转换、数据清洗、数据集成和剔除无效数据等预处理。随后对数据进行匹配，通过HDFS文件存储系统和Hbase数据库进行存储，使数据能传送到Spark实时数据处理平台上。

在该平台上，先将AIS数据转换成Stream数据，用Spark Streaming将其按6 min/段分割成若干片段，用batch批量处理这些数据，再采用Spark Engine高层算法处理，转变成一批批结果流。

2 构建航道交通拥堵判定模型

2.1 模型参数确定

1) 平均速度。船舶交通流平均速度是指单位时间内船舶平均对地速度，计算式为

(1)

式(1)中：u为船舶交通流平均速度；∑vi为船舶对地速度之和；n为船舶数量。

2) 区域密度。船舶交通流区域密度[9]是指单位矩形区域内存在的船舶数量，计算式为

(2)

式(2)中：k为船舶交通流区域密度；n为船舶数量；s为区域面积。

3) 临界密度。航道临界密度[2]分为转折密度和阻塞密度。转折密度指当船舶可安全畅行时，航道能允许的最大交通流密度；阻塞密度指船舶密集到难以移动时的交通流密度。本文根据阻塞密度提出一种新的航道交通拥堵判定方法。

4) 线密度。航道线密度实际上是区域密度的一种特殊形式，指航道单位长度上某个时间段内的船舶数量，计算式为

(3)

式(3)中：k为航道线密度；n为船舶数量；l为航道长度。

2.2 标准船舶艘次计算

船舶的大小会影响航道拥堵程度，故不能只考虑船舶艘次。将各船船长换算成标准船长，设置相应系数，将船舶艘次转换成标准船舶艘次[10](见表3)。标准船舶艘次的计算式为

S=Ciμi

(4)

式(4)中：S为标准船舶艘次；Ci为同类船舶艘次；μi为每类船舶的转换系数。

表3 船舶按船长分类后的转换系数

2.3 航道交通拥堵判定模型

根据藤井船舶领域模型[11]，在按船长分类之后，单船的船舶领域长轴计算式为

li=k0Li

(5)

式(5)中：li为单船的船舶领域长轴；Li为单船的船长；i的取值范围为1～n2；n2为船舶数量；k0为船舶领域长轴系数。

若要判断航道是否严重拥堵，须用到临界密度中的阻塞密度。阻塞密度等于临界船舶数量除以航道长度，是一种线密度。临界船舶数量是指船舶可安全畅行时航道内的最大标准船舶艘次。单船对应的航道阻塞密度分量的计算式为

(6)

式(6)中：ρ0i为单船对应的航道阻塞密度分量；n0i为单船对应的临界船舶数量分量；s0为航道长度。

临界船舶数量等于航道长度除以船舶领域长轴，n0i的计算式为

(7)

将式(7)代入式(6)可得

(8)

在计算各船的平均阻塞密度时，要考虑标准船舶艘次的影响，计算式为

(9)

式(9)中:Ci为单船对应的船舶艘次，均等于1;ρ0为航道阻塞密度;k0为船舶领域长轴系数，一般取1.5。[2]

判断航道是否严重拥堵，实际上是用航道实际密度与阻塞密度相比较。航道实际密度等于标准船舶艘次之和除以航道长度，计算式为

(10)

式(10)中:ρ1为航道实际密度;n1为标准船舶艘次之和。

借鉴公路交通拥堵判定方法，由表1可知，当V/C>1时，交通拥堵很严重。同理，若航道水域的总面积大于航道中所有船舶的领域之和，则航道处于严重拥堵状态，结合式(3)，可对ρ1和ρ0定义一个标准：若ρ1≥ρ0，则航道处于严重拥堵状态。

(11)

vi对应q个AIS点，计算式为

(12)

式(12)中:vij为vi在q个点中对应的第j个点；j的取值范围为1～q。

自由流速度u0是指畅通状态下的航道最高限速值，该值可定为8 kn。[12]

综上所述，判定航道交通状态的标准为

(13)

3 实例验证

3.1 长江南通段航道数据试验

该试验的数据来源于长江南通段，该航段见图2。试验于2017年2月6日10:00—10:05进行，初始数据个数m1=2 822。

选取东经120.5°～121.25°、北纬31.5°～32.5°的范围作为有效区域(见图3)。

选取东经120.85°～120.9°、北纬31.9°～31.95°范围内的小段航道作为研究区域，其数据个数m4=240，分类后有24艘船。将数据拟合成曲线1(见图4)。

在图4中，清除偏离主航道的数据，将剩余数据拟合成曲线2(见图5)。

取曲线2上的(120.860，31.952)和(120.882，31.903)2点作为该段航道的主航道的起止点，用式(14)求出其长度s0=5.829 8 km。

(14)

式(14)中:R为地球半径,约6 370 km;(x1,y1)和(x2,y2)为地球上任意2点。

试验结果见表4第1行。将10:00—10:59分成10段，重复进行试验，结果见表4。

表4 各时间间隔内的试验结果

将表4的拥堵状态判定结果与实际拥堵状态用折线图表示，结果见图6。

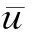
3.2 湘江湘阴段航道数据试验

该试验的数据来源于湘江湘阴段，该航段见图7。试验于2017年2月18日17:00—17:05进行，初始数据个数m1=301。

选取东经112.5°～113°、北纬28°～29°的范围作为有效区域(见图8)。

选取东经112.805°～112.815°、北纬28.57°～28.59°范围内的航道作为研究区域，其数据个数m4=77，分类后有10艘船。将数据拟合成曲线1(见图9)。

由于没有偏离主航道的数据，可取曲线1上的(112.805 2，28.571 0)和(112.811 8，28.590 0)作为该段航道的主航道的起止点，用式(14)求出其长度s0=2.208 5 km。

试验结果见表5第1行。将17:00—17:47分成8段，重复进行试验，结果见表5。

将表5的拥堵状态判定结果与实际拥堵状态用折线图表示,结果见图10。

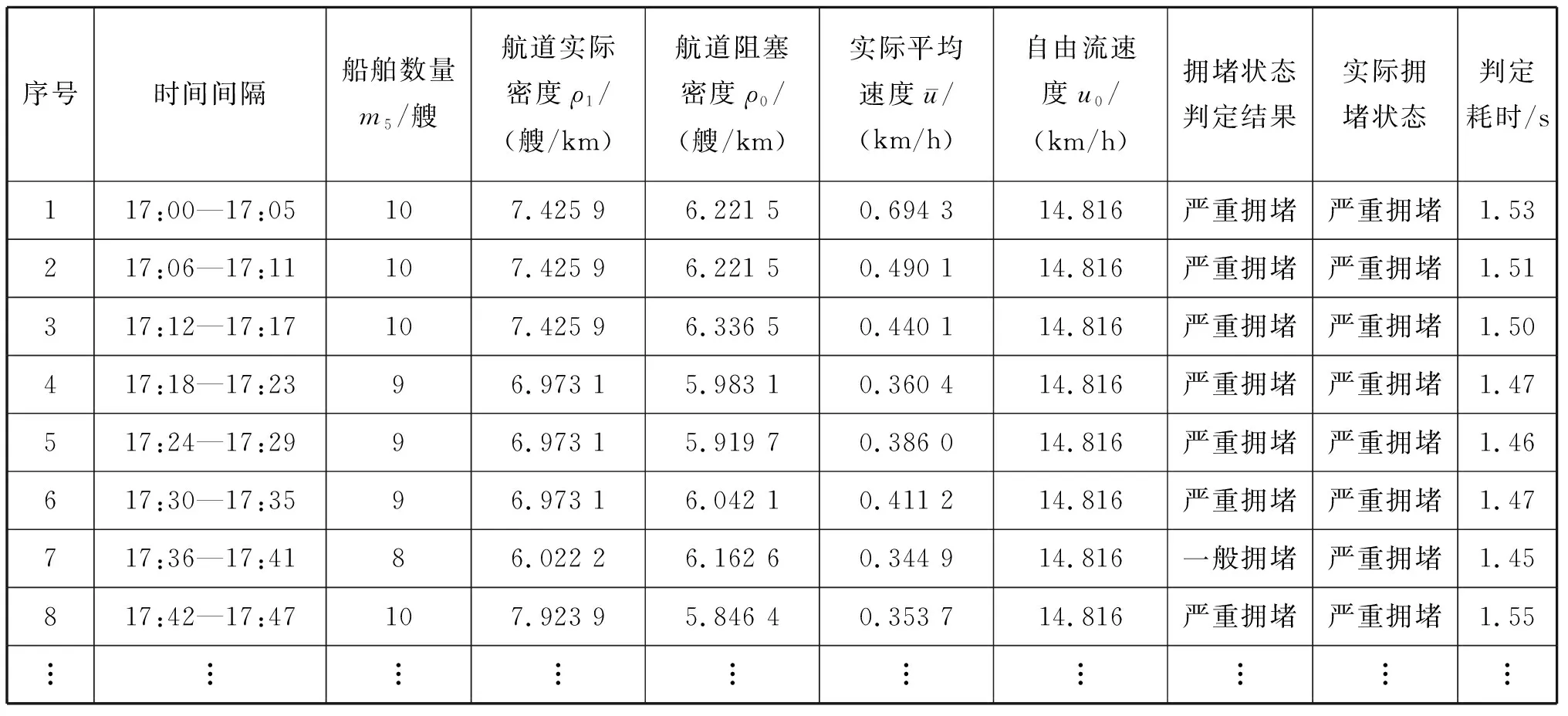
表5 各时间间隔内的试验结果

4 结束语

本文借鉴国内外道路交通拥堵判定方法，将航道交通状态划分为严重拥堵、一般拥堵和畅通等3种，运用交通流参数、标准船舶艘次和船舶领域模型，根据参数计算公式，构建航道交通拥堵快速判定模型。在Spark实时数据处理平台上实时处理AIS数据，运用该模型分别对长江南通段航道和湘江湘阴段航道进行多组在线试验。

试验结果表明:2段航道数据试验的判定准确率均达到80%以上，准确率较高；判定耗时均为1.50 s左右，判定速度较快；多次重复试验可使判定准确率达到90%以上。

本文提出的航道交通拥堵判定方法是一种全新的方法，考虑的参量与已有方法的参量有很大不同，思路也不一致，因此难以直接对比。本文的创新点和优势可概括为:

1) 实时性高，利用详细的AIS实时数据，实时运用判定模型，快速判定航道交通状态。

2) 利用计算机平台进行自动化判定，大大降低了人为因素的影响。

3) 判定准确率高，判定速度快，具有可重复性、可验证性，明确了航道交通状态的定量划分，克服了以往人工判定和事后判定的缺陷，可为海事部门实时掌握航道交通状态提供有效的技术支持。

[1] 刘予笑. 基于模糊综合评价的航道拥堵状态识别研究[D]. 杭州:浙江工商大学, 2015.

[2] 刘赛龙, 蒋璘晖. 内河航道服务水平及通过能力研究[J]. 水运工程, 2014(3):134-139.

[3] 刘明俊, 万长征. 航道通过能力影响因素的分析[J]. 船海工程, 2008,37(5): 116-118.

[4] 祝付玲. 城市道路交通拥堵评价指标体系研究[D]. 南京:东南大学, 2006.

[5] KNORR F, SCHRECKENBERG M. Influence of Inter-Vehicle Communication on Peak Hour Traffic Flow[J]. Physica A: Statistical Mechanics & Its Applications, 2012, 391(6): 2225-2231.

[6] LAKAS A, CHAQFEH M. A Novel Method for Reducing Road Traffic Congestion Using Vehicular Communication[C]//International Wireless Communications & Mobile Computing Conference, 2010: 16-20.

[7] 李文栋. 基于Spark的大数据挖掘技术的研究与实现[D]. 济南:山东大学, 2015.

[8] 李天喜. 基于Spark Streaming的试验数据处理系统的研究与实现[D]. 西安：西安电子科技大学, 2015.

[9] 冯宏祥, 孔凡邨, 肖英杰,等. 基于AIS的元胞自动机模型的船舶交通流特征参数分析[J]. 武汉理工大学学报(交通科学与工程版), 2014(2):324-328.

[10] 邓顺江, 刘明俊. 船舶领域模型的对比研究[J]. 中国水运, 2009, 9(6):7-9.

[11] 丁法. 基于AIS数据的开阔水域船舶领域分析研究[D]. 大连:大连海事大学, 2016.

[12] 徐春, 郑中义, 吴兆麟. 受限航道中船舶的限速[J].大连海事大学学报, 2002, 28(2):6-9.