装卸重大件货物对船舶稳性的影响

王玉闯， 史国友， 李伟峰

(1. 大连海事大学 航海学院， 辽宁 大连 116026； 2. 辽宁省航海安全保障重点实验室， 辽宁 大连 116026)

在大件货物装卸计算原理方面：文献[1]和文献[2]将装卸载荷对船舶浮态和初稳性的影响分为装卸小量载荷和装卸大量载荷2类进行探讨，分别给出计算方法和理论推导过程；文献[3]先给出一个通用公式，然后将少量装卸载荷作为一类特殊情况进行理论推导并提出直壁假设和初稳心不变假设2种假设方法。基于上述静力学理论推导，文献[4]在计算船舶初稳性和横倾角时均考虑吊杆仰角对计算结果的影响；文献[5]虽然也考虑吊杆仰角问题，但在运用计算公式推导时将模型理想化，简化了计算公式；文献[6]和文献[7]直接将整个装卸过程中吊杆的仰角理想化为不变。装卸过程中的横倾调整：文献[4]～文献[6]均采用调拨或注入(排放)压载水的方式；不同之处在于文献[4]和文献[5]将安全阈值设为3°，即在整个重大件装卸期间要求横倾角≤3°，而文献[6]要求横倾角≤12°。

对此，综合文献[2]和文献[3]所给计算方法的优点，联系航海实际，总结两者出现差异的原因，给出更具有通用性的计算方法,给出考虑吊杆仰角的公式推导过程及应用该公式时的注意事项，计算出在满足《2008年国际完整稳性规则》对初稳性要求条件下的“装载极限”，同时给出“大富”轮装卸过程中为调整横倾而具体采用的压载水调拨方案。

1 海运重大件货物的定义及特点

重大件货物的定义有一个演变的过程[8]，且各个国家和地区没有统一的标准，一般指单件体积过大或过长、质量超过一定界限的货物[9]，具体定义见表1。

表1 重大件货物定义

重大件货物除了具有定义中指出的超高、超宽、超长、超重和形状不规则等特性之外，其运作过程也具有复杂性和多变性等特点，是一个复杂的系统。大件货物通常应用在重要的基础和制造行业，具有显著的一次性和特殊性等特点。[10]目前专业的大件货物运输船舶不多，很难满足大件货物运输要求，一般采用多用途船或标准型散货船代替。[11]因此，重大件货物装卸过程中的稳性计算尤为重要，是船舶和船员安全的最基本保障，是避免稳性丧失、横倾过大酿成严重后果的有力保障。

2 装卸载荷对船舶浮态及初稳性影响的理论计算

装卸载荷必然会引起船舶排水量和重心发生改变，进而改变船舶的浮态和初稳性。综合文献[2]和文献[3]所提方法的优点，联系航海实际，总结出两者出现差异的原因，文献[3]的计算方法更具有通用性。

2.1 装卸少量载荷对船舶初稳心高度的影响

在船上任意位置处增加载荷会使船舶的吃水增加，并产生横倾和纵倾。在理论计算中，可在保证计算精度的基础上做一些假设和简化，具体分为以下2个步骤[12]讨论：

1) 船舶平行沉浮，即假定载荷装载的位置在水线面漂心F上。

2) 将载荷移到指定位置，以确定船舶的横倾。

由船舶静力学原理可知：

(1) 船舶平行沉浮，有

δd=m/(100TPC)

(1)

(2) 重心发生变化，有

(2)

(3) 浮心发生变化，有

(3)

(4)

(4) 假设船舶水线面附近为直舷壁，则装卸前后水线面形状不变，水线面面积惯性矩不变，有

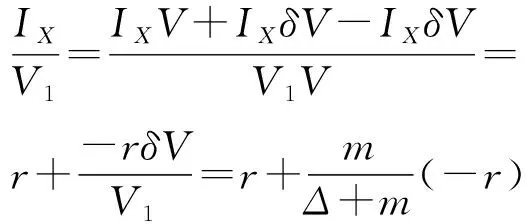
(5)

联合式(2)、式(4)和式(5)得装卸载荷后船舶初稳心高度为

(6)

(7)

2.2 装载任意质量载荷对船舶初稳心高度的影响

装载重物前后，船舶吃水、漂心、浮心、稳心和重心等均有变化，可根据初稳心高度的定义求取装卸重物之后的初稳心高度。[14]

1) 计算装卸重物之后船舶的质量和重心。

(1) 装卸重物之后船舶的排水量为

(8)

(2) 根据合力矩定理求装卸重物之后船舶的重心位置，有

(9)

2) 根据装卸重物之后船舶的排水量Δ1，查静水力参数资料，得到等容平均吃水d1、船舶稳心距基线的高度KM1和浮心位置等参数。

3) 计算装卸重物之后船舶的初稳心高度，有

hG1M1=KM1-KG1

(10)

上述计算方法存在差别的主要原因是计算机技术的迅猛发展使得船舶设计单位或船厂能直接给出详细的静水力性能参数，原来的静水力曲线图逐渐变成现在的参数表，这种“图”到“表”的转变使计算方法得到进一步拓展。图1给出的是某船静水力性能参数表的部分截图。

由图1可知，静水力性能参数表的吃水间隔仅为5 cm，因此利用该方法计算船舶装卸重物前后的初稳心高度不仅方便，而且准确。

2.3 装卸载荷所引起的船舶横倾

假设装卸重物之前船舶为正浮状态，装卸后船舶会因产生相应的横倾和纵倾而变为任意浮态。本文只研究装卸载荷产生的船舶横倾，即假设船舶为单纯横倾。式(9)给出装卸重物之后船舶的重心位置，若yg1≠0，则船舶存在横倾角满足

tanθ=(myg1)/(Δ1hG1M1)

(11)

3 装卸大件货时对船舶稳性的影响

一般装卸大件货的重吊的起重能力为几十吨至几百吨，虽然单件大件货远比一般货物重，但与排水量相比，二者的差值仍≪10%，“大富”轮夏季满载排水量为24 305 t，货舱克令吊起重能力为250 t，显然远小于10%的排水量。因此，在计算装卸大件货时船舶的稳性时，仍可按照少量装卸货物来处理。

3.1 吊卸作业

船上重吊在吊卸大件货离船的整个过程中所遇到的问题都属于船内问题。[15]即货物在吊离初始装载位置至卸落码头之前一直保持悬挂状态，而当货物横向移动偏离装载位置垂线之后，便以起吊设备底座为中心作变半径弧形水平移动。

3.1.1吊卸过程中船舶初稳性计算

货物在整个吊卸过程中的运动可分为垂向和横向2个方向的运动，其中仅有垂向移动影响重心，即改变船舶的初稳性。因此，在整个吊卸过程中，船舶初稳性的减小量仅与吊杆的仰角α有关，船舶稳心减小量δGM的计算式为

(12)

式(12)中：δGM为吊卸过程中船舶初稳心减小量，m；m为卸货件质量，t；lb为吊杆臂长,m;mb为吊杆质量，t；α为吊杆仰角，(°)；D为船舶型深，m；zp为所卸货物的位置坐标(zp，yp)，m；Δ为吊卸货物前船舶的排水量，t。

由船舶原理相关知识可知，此时船舶的复原力矩可表示为

Ms=ΔhGM-P(lbsinα+D-zp)-

(13)

式(13)中：θ为船舶横倾角。

由式(12)可知，在整个货物吊卸过程中，船舶的初稳性减小仅与吊杆的仰角有关，且船舶初稳性最小处出现在吊杆仰角最大位置处。一般情况下，吊杆仰角的最大值出现在吊卸重物的初始阶段，最小值出现在卸落码头阶段。

3.1.2吊卸过程中船舶横倾角的计算

横移将影响船舶的横倾，此时由于货物横移而产生的船舶横倾力矩Mh可表示为

Mh=mycosθ+mby′cosθ

(14)

式(14)中：Mh为 横倾力矩；y为货物横移距离；y′为吊杆重心横移距离。

式(14)中的货物横移距离y和吊杆重心横移距离y′可进一步展开为

(15)

式(15)中：yp为所卸货物的位置坐标(zp，yp)，装载于远离码头一舷取正值，装载于靠近码头一舷取负值；β为吊杆偏离船舶中纵面水平旋回角。

根据横倾力矩与稳性力矩平衡的条件，联立式(13)和式(14)，得出船上重吊吊卸重物时的瞬时船舶横倾角表达式为

(16)

由式(16)可知，船舶在吊装货物时产生的横倾角与吊卸过程中吊杆的仰角α和水平旋回角β有关，最大横倾角出现在吊杆仰角与水平旋回角最大时。因此，在整个吊卸货物过程中，横倾角的极值一定出现在吊杆仰角最大处(α≤90°)。根据实际生产状况，在将货物卸落至码头时，吊杆的仰角通常有所减小，因此横倾角的极值并非在卸落前出现。然而，考虑到在吊卸过程中若干参数的随机性和计算的简便性，在实际应用时均将卸落前的瞬间作为横倾角极值出现的时刻。因此，式(16)可简化为

(17)

式(17)中：B为船宽；l为舷外跨距；zb为货物悬挂点垂向坐标。

3.2 吊装作业

吊装大件货与吊卸货物类似，只是船舶的排水量发生了变化，推导方法和研究思路及得出的结论与“3.1”节相同。为简便起见，这里仅给出最后的计算式和结论。

3.2.1吊装过程中船舶初稳性计算

船舶稳心减小量δGM的计算式为

(18)

由式(18)可知，在吊装货物过程中，船舶初稳心的减小同样仅与吊杆的仰角有关，且船舶初稳性最小值出现在吊杆仰角最大的位置处。一般情况下，吊杆仰角的最大值出现在重吊旋至拟装舱位的上方时，最小值出现在吊离码头时。

3.2.2吊装过程中船舶横倾角的计算

船上重吊吊装重物时的瞬时船舶横倾角的表达式为

(19)

与吊卸过程一样，式(19)可简化为

tanθ=

(20)

式(18)～式(20)中：KG为装货前船舶重心高度；l为吊杆跨距。

3.3 装卸过程中的横倾调整

船舶在装卸过程中应尽量保持正浮状态，前已述及，无论是吊装还是吊卸，势必会造成船舶横倾角发生变化。为保障船舶和船员的安全，按照国际惯例，通常要求在整个装卸过程中船舶的横倾角≤3°。因此，在吊装或吊卸作业前要对此次作业进行细致的计算校核，查验是否满足整个装卸过程中横倾角均≤3°，若不满足，应通过调拨或注入(排出)压载水予以调整。

利用调拨或注入(排放)压载水的方法调整船舶装卸货期间任意时刻横倾角所需压载水质量mw的通用表达式为

mwy′cosθ=Mh

(21)

式(21)中：mw为所需压载水质量；y′为压载水调拨横倾力臂。

在卸货或装货过程中，所需调拨或注入(排放)压载水质量mw的具体计算式见表2。

表2 货物装卸过程中欲调拨压载水量

3.4 实船计算

“大富”轮的参数见表3。

表4给出“大富”轮货舱克令吊的技术参数。

由表4可知，克令吊的最大安全工作负荷为250 t，吊臂长为27 m。为便于计算，将用于船舶稳性计算的数值标注为图2的形式，其中：lb为吊臂长度；H为克令吊底座高度；D为船舶型深。

表3 “大富”轮参数

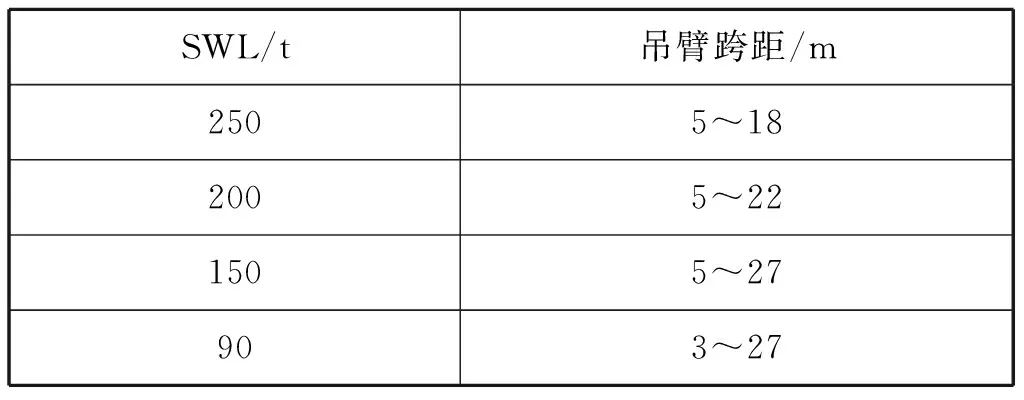
表4 “大富”轮货舱克令吊技术参数

以某航次为例，所装货物为桥梁和火电设备，单件货物最重为220 t。根据式(18)可计算出此次吊装货物导致的船舶稳心减小量的数值，将计算所需基础数据汇总于表5中。

将表5中的数据代入到式(18)中可得到此次吊装货物造成的船舶初稳心减小量为δGM=-0.33～1.24 m,即船舶初稳心的减小仅与吊杆仰角有关，吊杆仰角越大，对船舶初稳性的影响越大，即船舶初稳心最小值出现在吊杆仰角最大的位置处。在实际操作中，一般吊杆仰角α最大为60°，将该值代入到式(18)中求得船舶初稳心减小量δGM=1.14 m。

将表5中的数据代入到式(20)中可得到此次吊装货物造成的船舶横倾角满足tanθ≈0.077 6。

在以上计算中，吊杆跨距取的最大值为27 m，求得的横倾角为最大值θ≈4°26″。

由上述分析和实船计算可知，装卸重大件过程中的稳性降低或产生的横倾角可通过侧翼压载的方式减小。通过运用考虑吊杆仰角的计算方法，对“大富”轮在吊杆最大工作载荷情况下的“极限装载”进行计算，单次吊装货物可对“大富”轮产生船舶初稳心减小1.14 m、横倾4°26″的影响，对船舶装卸货物操作实践具有理论指导意义。

表5 计算所需的基础数据

4 结束语

给出装卸载荷对船舶浮态和初稳性的影响的理论计算通用方法，从考虑吊杆仰角的角度给出整个吊装、吊卸作业过程中产生的船舶初稳心降低及横倾的具体推导过程。船舶初稳性的变化仅与吊杆的仰角有关，运用该方法对单次吊装货物进行计算，结果产生船舶初稳心减小1.14 m、横倾4°26″的影响，通过调拨压载水可调整装卸重物引起的船舶横倾，对船舶装卸货物操作实践具有理论指导意义。

[1] 孙承猛,刘寅东.船舶浮态计算的一种优化方法[J].大连海事大学学报，2016(2)：39-41.

[2] 盛振邦，刘应中.船舶原理(上册)[M].上海：上海交通大学出版社，2003:46-70.

[3] 杜嘉立.船舶原理[M].大连：大连海事大学出版社，2008:47-57.

[4] 徐邦祯，姜华.重大件货物装卸中船舶稳性的计算及调整[J].大连海事大学学报，2003，29(1)：50-52.

[5] 高亮，田佰军，李士国.船载重大件货物应注意的几个问题[J].航海技术，2013，6(5)：32-33.

[6] 杨洲.船舶装卸重大件货物方案设计研究[D].大连：大连海事大学，2015:20-26.

[7] 叶章云.重大件货物吊装及积载的计算机辅助设计研究[D].大连：大连海事大学，2002:7-27.

[8] 徐俊菁.珠三角地区集装箱运输发展问题研究[D].大连：大连海事大学，2007:2-7.

[9] 安宇鸣，张仁颐.重大件海洋物流的典型货盘及装运方式[J].物流科技，2007,30(12)：37-39.

[10] 曹刚．大件物流运营与组织问题研究[D]．成都：西南交通大学，2011:5-10.

[11] 陈毅.浅析大件物流运营与组织问题[J].低碳世界，2016(16)：199-200.

[12] 蒋璐，唐娟娟，胡以怀.液货船稳性计算及校核方法研究[J].造船技术，2015(1)：20-24.

[13] 任凯,浦金云,李营.船舶装载对初稳性影响的实验教学模型[J].实验室研究与探索,2014,33(7):180-184.

[14] 段兴锋,任鸿翔,东昉.纵倾状态船舶浮态的研究与计算[J].中国航海,2015,38(1):54-57.

[15] 蒋维清.船舶原理[M].大连：大连海事大学出版社，1998:90-99.