基于Hilbert-Huang变换的航天器发射段力学环境分析
武江凯,白明生
(1.哈尔滨工业大学 航天学院,哈尔滨 150001; 2.中国空间技术研究院 载人航天总体部,北京 100094)
0 引言
载人航天器从发射到最后返回着陆,要经历发射段、在轨运行段和返回段中的各种噪声、振动、冲击和加速度等复杂力学环境。对飞行任务中力学环境参数的深入分析,对于制定和修改地面力学环境试验条件,从而指导设计,提高载人航天器对飞行环境的适应性、可靠性具有重要意义。采用正确合理的方法对测量到的振动时间历程信号进行识别处理是完成载人航天器力学环境分析的关键一步,除了完成信号时域内时间历程分析外,还需要针对不同类别的信号采用不同的特殊处理方法,以获得信号的特征信息[1-3]。
当前信号处理中常用的傅里叶变换(FFT)方法,是首先假定待处理信号具有线性、稳态特性,否则频谱分析结果可能没有物理意义;但实际信号通常是有限长、非线性且/或非平稳的。因此,基于FFT的频谱分析在实际应用中常常受到很大的限制。另外,FFT虽然可以分别从时间和频率2方面信号进行特征分析,但无法同时保留时间和频率信息,此外还存在能量在频域内发散以及造成部分负能量泄漏等问题[4]。
近年来,研究人员在时频分析研究方面取得了许多成果,先后提出了短时Fourier变换、Winger-Ville分布、Choi-Williams分布和小波变换等有效信号分析方法。但这些方法都采用积分作为分析手段,其基函数都为固定形式,缺乏自适应性,且容易出现多余信号,无法准确描述频率随时间的变换。1998年,Huang等人在提出经验模态分解方法的基础上,提出了Hilbert-Huang变换(HHT)方法[5]。该方法可以根据信号本身自适应生成基函数,对非平稳信号中的各频率成分进行有效分离,进而得到信号的Hilbert谱与Hilbert边际谱,最终实现对信号的时频分析,对于非平稳复杂信号具有很好的处理效果。
本文基于HHT的原理及特点,对某载人航天器发射过程中整流罩分离期间的瞬态力学环境参数进行处理,得到信号的主频率及对应时间范围,旨在为地面力学试验条件制定以及运载接口条件确定提供参考。
1 Hilbert-Huang变换基本原理
HHT作为一种具有自适应性的时频分析方法,在无须人为干预情况下,能够对信号的局部时变进行自适应的时频分解,非常适合用于对非平稳信号的时频分析。时频分析的关键在于确定信号的瞬时频率,而实际信号大多为复杂的多分量信号,计算瞬时频率时需要将其分解为单分量。为此,Huang等人提出了经验模态分解(emperical mode decomposition,EMD)法,可将待处理信号分解为单分量的固有模态函数( intrinsic mode function,IMF),然后在IMF的基础上计算瞬时频率并构造时间−频率−幅值三维Hilbert谱。
1.1 瞬时频率
一般情况下,非平稳信号的频率和幅值都相对时间变化,目前,提取信号瞬时频率的方法有多种,包括解析信号法、Shekel算法、Teager-Kaiser算法等,其中解析信号法最为合理、适用[6-8]。
针对解析信号,Ville对瞬时频率的定义进行了统一,即定义信号x(t)=a(t)cosθ(t) 的瞬时频率为
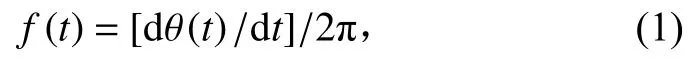
即信号相位的一次求导[9]。
在HHT中,可通过Hilbert变换求解局部相位微分的方法得到信号的瞬时频率。
对于实际待处理信号x(t),其解析信号为

式中:y(t)为x(t)的Hilbert变换,

其中p为Cauchy主值;a(t)为单分量信号的瞬时幅值,

θ(t)为单分量信号的瞬时相位,

在瞬时频率的基础上,可以应用波间频率调制解释波形的非线性变化,应用波内频率调制解释波形的散射传播。
1.2 固有模态函数(IMF)
实际信号多为复杂的多分量信号,其瞬时频率无法直接计算。因此,在以往的应用中,为了使求解的瞬时频率具有实际意义,一般要求信号须满足窄带条件。Huang推广了窄带条件的要求,并将具备以下特征的信号定义为IMF:
1)待处理信号中,极值点数目和过零点数目相差≤1;
2)任意时刻点,由局部极大值和局部极小值定义的信号上下包络均值为0。
1.3 经验模态分解(EMD)与Hilbert谱
HHT的核心是EMD。EMD方法根据信号的局部时间尺度,可自适应地筛选生成IMF,并将信号展开为若干IMF叠加之和的形式,以便由IMF计算瞬时频率。类似于Fourier变换和小波分解,EMD以IMF作为基函数进行非平稳信号分解是完备、自适应的,而且在实际应用中是几乎正交的。
对于实际信号x(t),EMD的具体算法如下:
1)初始化:令r0(t)=x(t),i=1。
2)筛选第i个 IMF:
a.初始化:令j=0,hij(t)=ri−1(t);
b.确定hij(t)的局部极值,包括极大值和极小值;
c.应用3次样条对信号进行插值,分别通过局部极大值和局部极小值构造信号hij(t)的上下包络;
d.计算已构造上下包络信号的瞬时均值mij(t);
e.令hij(t)=hij(t)−mij(t);
f.若hij(t)满足IMF筛选终止条件,则令第i个 IMFci(t)=hij(t),否则,令j=j+1,并返回步骤 b。
3)令ri(t)=ri−1(t)−ci(t)。
4)若ri(t)满足EMD的终止条件,则认为ri(t)为残余信号,并结束分解过程;否则,令i=i+1,并返回步骤2)。
其中,单个IMF的筛选通过对连续2次筛选结果之间的标准差σ进行控制,
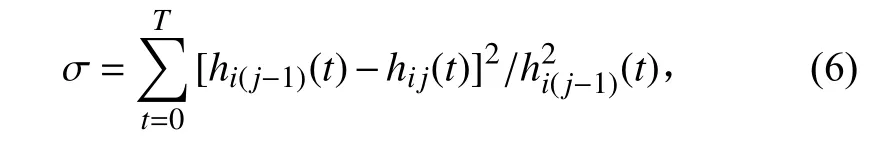
其中T为信号总长度,σ∈[0.2,0.3]。
根据EMD分解结果,非平稳信号可以表示为
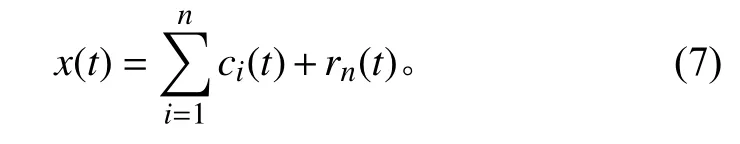
Hilbert谱是信号的时间−频率−幅值三维表示。对式(7)进行Hilbert变换,以极坐标形式构造解析信号,并取信号实部,则可得到Hilbert幅值谱

H(t,f)精确描述了信号幅值在整个频率段上随时间和频率的变换规律。由式(8)可见,若将IMF视为基函数,由于其幅值和频率是时变的,则相对传统的Fourier分析而言,Hilbert幅值谱可以视为Fourier频谱的推广形式,能够识别非平稳信号的幅值和频率时变特征。
Hilbert边际谱的定义为

Hilbert边际谱给出了信号幅值在整个频率段上的变换情况,以及每个频率值对整个时间范围的贡献测度,表示了统计意义上所有数据长度的累加幅度。
由于EMD的自适应广义基性质,H(t,f)和H(f)都可以比较准确地反映信号的实际成分,即只要存在某一频率成分,则表示该信号中一定有对应频率的振动波动存在[10-11]。
2 HHT在载人航天器力学环境分析中的应用
应用Hilbert-Huang时频联合分析方法对某载人航天器整流罩分离期间采集到的低频振动信号进行分析,建立信号的幅值/能量−时间−频率三维Hilbert-Huang谱。典型HHT分析的过程如图1所示。
利用HHT对整流罩分离期间采集到的信号进行处理分析,计算出瞬时频率、瞬时相位及各分量的EMD值(参见图2),求取信号的Hilbert-Huang时频谱(见图3)。
图3中:横轴代表时间变化;纵轴代表信号中的主要频率成分,颜色的深浅代表能量的高低,图中最下面一条频率曲线的颜色最深,代表其能量最高。从图3可以看出,在0.07 s时,信号的频率发生了突变,且能量随时间迅速衰减,说明组合体在这一时刻经历了一个强烈变化的力学载荷。

图1 Hilbert-Huang 变换过程Fig.1 Flow chart of the Hilbert-Huang transform
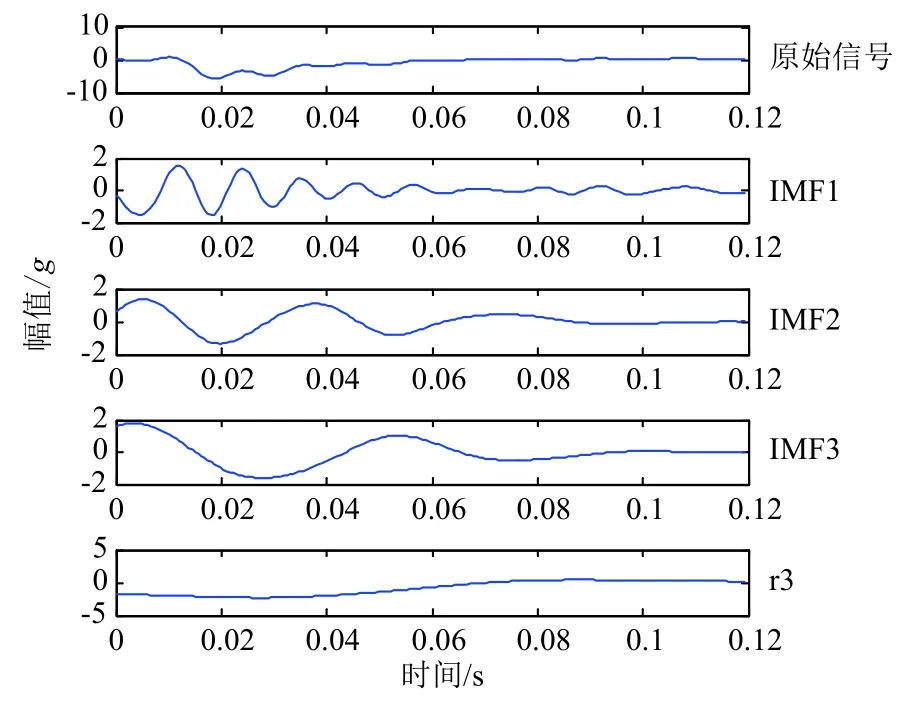
图2 原始信号及 EMD 得到的各分量Fig.2 Original signal and the components of the signal based on EMD
图4为整流罩分离信号边际谱,从图中可以看出,整流罩分离信号的能量主要集中在约40 Hz处,与图3形成了较好的对应。参考文献[12]给出,整流罩分离期间低频瞬态信号频率不超过50 Hz,因此图3的最下面一条曲线为信号的主分量,即在发射段整流罩分离期间,载人航天器主要经受了频率约为40 Hz的低频振动载荷作用。

图3 整流罩分离信号二维时频谱Fig.3 2-D Time-frequency spectrum during the separation of fairing

图4 整流罩分离信号边际谱Fig.4 Marginal spectrum during the separation of fairing
3 结束语
本文在HHT分析的基本方法基础上,针对载人航天器发射段非平稳振动信号的处理需求,应用HHT方法对载人航天器发射段整流罩分离期间船箭对接面的振动信号进行处理分析,得到了时频联合域内时间−频率−幅值三维Hilbert谱。Hilbert-Huang时频谱可以比较准确地识别出信号中的主能量和频率成分,及其出现的大致时间范围,且具有较好的时频分辨率。
对某载人航天器整流罩分离期间的实际数据进行处理,得到在0.09 s时刻,舱箭组合体经历了频率为40 Hz的强烈振动,表明HHT方法具有能同时给出时频域信号的优势,对于处理载人航天器发射段非平稳信号有较好的适用性,可以更方便地对飞行事件发生时信号的频谱进行识别和定位,可用于后续任务飞行参数的处理,服务于地面力学试验条件制定与运载接口条件确定。
[1]马兴瑞,于登云,韩增尧,等.星箭力学环境分析与试验技术研究进展[J].宇航学报,2006,27(3):323-331 MA X R,YU D Y,HAN Z Y,et al.Research evolution on the satellite-rocket mechanical environment analysis and test technology[J].Journal of Astronautics,2006,27(3):323-331
[2]马兴瑞,韩增尧,邹元杰,等.航天器力学环境分析与条件设计研究进展[J].宇航学报,2012,33(1):1-12 MA X R,HAN Z Y,ZOU Y J,et al.Review and assessment of spacecraft mechanical environment analysis and specification determination[J].Journal of Astronautics,2012,33(1):1-12
[3]朱亮聪,褚洪杰,毛玉明,等.基于部分遥测数据的飞行器力学环境评估方法[J].上海航天,2015,32(5):44-47 ZHU L C,CHU H J,MAO Y M,et al.Estimation of mechanical environment for spacecraft using partly remote measured data[J].Aerospace Shanghai,2015,32(5):44-47
[4]冯志鹏,褚福磊.基于Hilbert-Huang变换的水轮机非平稳压力脉动信号分析[J].中国电机工程学报,2005,25(10):111-115 FENG Z P,CHU F L.Transient hydraulic pressure fluctuation signal analysis of hydroturbine based on Hilbert-Huang transform[J].Proceedings of the CSEE,2005,25(10):111-115
[5]HUANG N E,SHEN Z,LONG S R,et al.The empirical mode decomposition and the Hilbert spectrun for nonlinear and non-stationary time series analysis[C]//Proceedings of the Royal Society of London A:Mathematical,Physical and Engineering Sciences,1998
[6]冯志鹏,褚福磊.行星齿轮箱故障诊断的频率解调分析方法[J].中国电机工程学报,2013,33(11):112-117 FENG Z P,CHU F L.Frequency demodulation analysis method for fault diagnosis of planetary gearboxes[J].Proceedings of the CSEE,2013,33(11):112-117
[7]高庆,朱辰,蔡毅鹏,等.飞行器力学环境参数分布特性及飞行散差研究进展[J].航天器环境工程,2016,33(5):555-561 GAO Q,ZHU C,CAI Y P,et al.A review of distribution and flight-to-flight variability of vehicles’ dynamic environment parameters[J].Spacecraft Environment Engineering,2016,33(5):555-561
[8]杨阳,李春,叶柯华,等.基于 HHT 方法的非稳定工况风力机结构动态响应时频特性分析[J].振动与冲击,2016,35(21):22-28 YANG Y,LI C,YE K H,et al.Structural dynamic response characteristics of a wind turbine in timefrequency domain under non-stationary operating conditions based on HHT method[J].Journal of Vibration and Shock,2016,35(21):22-28
[9]相小谊.基于Hilbert-Huang变换的信号分析及应用[D].西安:西安电子科技大学,2008:13-14
[10]孔宪仁,熊怀,李海勤,等.一种 Hilbert变换法在非线性系统分析中的应用[J].机械工程学报,2016,52(19):95-101 KONG X R,XIONG H,LI H Q,et al.The modified method of Hilbert transform and application in nonlinear vibration analysis[J].Journal of Mechanical Engineering,2016,52(19):95-101
[11]杨海,程伟.基于EMD及PNN的航天器振动环境分析[J].北京航空航天大学学报,2008,34(6):622-626 YANG H,CHENG W.Environment analysis based on PNN and EMD for vibration of spacecraft[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(6):622-626
[12]陈烈明.航天器结构与机构[M].北京:中国科学技术出版社,2005:20-37

