本地差分隐私保护及其应用*

高志强，崔翛龙，周 沙，袁 琛

(武警工程大学乌鲁木齐校区,新疆 乌鲁木齐 830049)

1 引言

随着互联网、云计算技术应用领域的不断扩张和大数据分析技术的飞速发展，海量数据在个人、企业、研究机构等源源不断地产生。无论是互联网巨头还是各种社会组织越来越钟情于收集和分析用户数据[1]。例如，浏览器(Browser)和移动应用软件(Mobile APP)无时无刻地通过收集用户终端数据来训练机器学习模型，分析用户行为模式；社会服务类企业会收集用户的生活统计数据来制定相应个性化服务方案[2 - 4]。收集用户数据是把双刃剑，第三方直接收集用户信息不利于保护用户隐私，然而不准确地收集用户信息，相应的服务质量就很难得到反馈提升，这样也不利于公共利益。因此，在数据收集阶段引入隐私保护机制来降低并控制隐私泄露的风险，平衡隐私保护与数据可用性之间的关系，解决和完善针对不牺牲用户个人隐私的大数据分析问题和机制是极具理论和实际意义的。

从1977年Dalenius[5]提出的隐私控制的定义，到经典数据脱敏方法k-anonymity[6]及其改进模型[7 - 11]都存在着以下缺陷：(1)集中存储模型下，非可信数据管理者使用户无法直接控制个人隐私数据。(2)由于背景知识无法明确界定，基于等价类的隐私保护模型被迫随着新攻击技术的出现而不断被动调整。(3)无法提供严格且有效的数学理论来证明其隐私保护水平，无法定量分析隐私泄露风险。值得重视的是，即使被严格处理的数据也可能泄露用户隐私，被去匿名化后的Netflix Prize竞赛历史数据信息[2,12]，便可以通过数据关联(Linkage)推断出用户具体隐私信息。

尽管早在2006年微软研究院的科学家Dwork[13 - 17]提出了严格可证明的差分隐私保护技术DP(Differential Privacy)，但由于仍然需要第三方来管理用户隐私数据，差分隐私一直是停留在理论研究层面的隐私定义，未被大规模地应用于实际产品中。因此，为平衡“个人隐私”和“大数据分析”关系，满足差分隐私保护特性，提高保护机制的隐私性和可用性，众包模式下的本地差分隐私保护LDP(Local Differential Privacy)[2,12,18]的概念应运而生。LDP可以在不需要信任第三方数据管理者的情况下，直接在本地将隐私数据加噪来保护个人信息不被泄露，同时从宏观角度保证数据收集者可正确地推断出群体统计信息。

目前，LDP技术已被广泛应用于集值型流式频繁项集挖掘的Heavy Hitters估计、众包模式下字符串边缘频率估计和联合概率估计、针对智能设备的机器学习等领域。值得关注的是，2014年，谷歌工程师Erlingsson等人[12]将基于随机应答和BloomFilter的RAPPOR(Randomized Aggregatable Privacy-Preserving Ordinal Response)技术成功应用于Google Chrome中，在本地通过差分隐私机制收集用户数据，首次揭开了LDP技术大规模应用的面纱。随后，Fanti等人[2]提出加强版的RAPPOR，实现了数据字典未知情况下的本地学习多变量联合概率分布估计。另外，2016年苹果全球开发者大会WWDC2016(WorldWide Developers Conference)[19]上，苹果软件工程高级副总裁Federighi在Keynote中宣布IOS10的QuickType输入法、emoji建议、spotlight全局搜索和备忘录关键词标记，将采用“差分隐私保护技术”在设备终端本地收集用户数据，并将隐私数据分析限制在用户设备上，并不会将数据上传到苹果服务器。随后，2017年6月，圣何塞McEnery会议中心的苹果开发者大会(WWDC2017)[20]发布了面向开发者的机器学习API——CoreML，继续强调用户数据隐私的重要性，保证机器学习的数据处理在个人设备上完成，也就是说，个人数据不必离开用户设备，用户信息将不被发送到云端，因而用户也能更好地获得隐私保护权益。

因此，作为差分隐私研究的重要分支，LDP技术正在从理论研究走向大规模实际业界产品应用，并逐渐成为差分隐私保护领域的一个研究热点。近几年来，LDP技术及其在各领域研究的结合使得大量新的成果不断涌现。本文在总结已有研究成果的基础上，对LDP理论发展及其在数据收集与数据分析领域的应用进行综述，希望能够为该领域的研究者提供有价值的参考信息。

2 预备知识

2.1 差分隐私定义下的数据模型

差分隐私是不依赖于攻击者背景知识的具有严格数学理论支撑的隐私定义，结合其应用场景及针对数据处理和收集方式的不同，主要存在两种数据分布模型：集中式模型，又称为可信管理者模型(Trusted Curator)[3]和本地模型(Local Model)[1]，如图1所示。

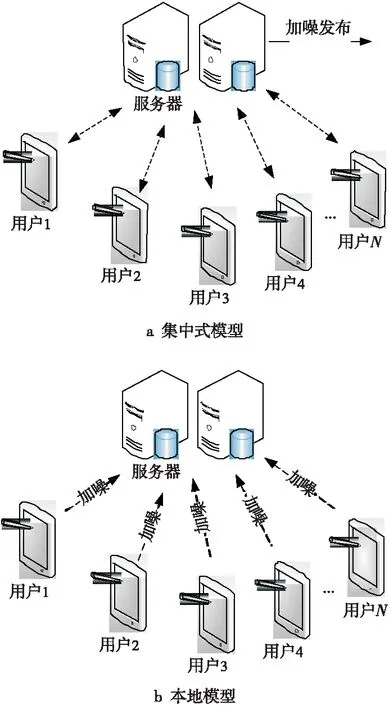
Figure 1 Data model in differential privacy图1 差分隐私定义下的数据模型

传统的集中式模型基于可信第三方，用户终端与数据收集者被视为一个数据收集与分析的整体，而数据服务器(云端)直接存储未处理的原始用户隐私数据，经过隐私处理(如加噪)等方式后统一对外发布。同时，集中式模型下又可以分为交互式和非交互式框架，目前，针对集中式差分隐私保护模型已有大量的研究成果[13,17,21 - 24]。Roth等人[21]提出了交互式数据发布的中位数机制(Median),能够在相同预算下提供更多数量的查询。Xu等人[22]提出了一种基于k-d树的直方图发布算法DPCube，当参数(频数分布紧密度阈值、空间分割次数)的取值适当时，DPCube算法在查询数量和查询误差等方面具有很好的性能。此外，Engel等人[23]提出了小波变换方法(Privelet),Hay等人[24]提出了层次查询方法，然而，这些针对差分隐私的数据发布和分析技术都基于可信管理者模型数据分布模型，集中式数据管理不可避免地面临着巨大的隐私安全泄露风险，严重制约着隐私保护技术的发展。

在众包模式下的分布式本地模型中，数据收集者(Data Collector)不可信任，数据服务器(云端)只能收到用户加噪的数据，也就是说，数据收集者根本不可能收集到原始数据。其中，用户在向数据收集者发送个人数据前，先在本地加入满足差分隐私的噪声扰动，最后数据收集者根据收集到的噪声数据，从统计学的角度近似估计出用户群体的统计特性，而不是针对具体用户个体进行统计特性推断。其中，每个用户只与数据收集者分享原始数据的加噪版本，由差分隐私保护的原理容易证明，无论本地隐私保护机制的加噪输出如何，都不能确定性地分析出具体的某一条记录来自于哪个用户个体，这既保证了群体统计信息的相对准确性，又保护了个人精确的原始数据，从而解决了用户隐私数据被不可信第三方外包管理的症结。

目前，针对本地模型的隐私保护算法研究不断涌现，文献[2]和文献[12]基于随机响应和BloomFilter，实现了用户字符串的统计信息的收集和多次数据收集的长效隐私保护。文献[3]结合本地隐私保护和集中式数据模式，提出具有高可用性和隐私保护性的混合模型BLENDER。文献[1]从生成式对抗神经网络的角度，结合差分隐私保护机制产生内部攻击数据，对协同式深度学习的安全性提出了挑战。文献[25]针对三星的智能移动终端的隐私数据收集问题，利用本地差分隐私保护机制构建了准确高效的Harmony系统，实现了支持LDP的统计分析与机器学习功能。综上所述，基于本地模型的最新研究成果涉及多个新兴领域，无论是基于统计分析的理论研究[18,26,27]还是产品实现，都将LDP的研究推向一个前所未有的高度。

2.2 本地差分隐私保护

LDP技术是解决基于非可信第三方隐私数据收集的方法，其主要思想是保证收集者：(1)不能收集或拥有任何个人的精确信息；(2)可以推断出用户群体的泛化统计信息。具体来说，用户在本地通过差分隐私技术来置乱原始数据，然后再把加噪数据发送给收集者。这样，LDP既保护了用户隐私，也避免了收集者面临的隐私数据治理的问题。本节将介绍差分隐私保护模型的两种形式化定义及定理。

定义1((ε,δ)-DP)[13]随机算法A满足(ε,δ)-DP，当且仅当所有邻接数据库D和D′只相差一条用户记录，对于算法A所有可能的输出R⊆Range(A)满足如下不等式：

Pr(A(D)∈R)≤eεPr(A(D′)∈R)+δ

(1)

其中，ε为隐私预算，用来调节算法A输出结果的隐私保护程度，适用于集中式差分隐私模型和本地差分隐私模型。

定义2((ε,δ)-LDP)[18]随机算法A满足(ε,δ)-LDP，当且仅当所有用户端数据对x1和x2，对于算法A所有可能的输出R⊆Range(A)满足不等式:

Pr(A(x1)∈R)≤eεPr(A(x2)∈R)+δ

(2)

当δ=0时，式(2)成为ε-LDP。直观地说，不管用户端数据的改变量，数据收集者关于接收到用户发送数据的背景知识改变不大。

两种差分隐私保护模型的主要区别如表1所示，二者最重要的差别在于加入噪声扰动的时机不同。在本地模型中，数据在发送给收集者之前进行隐私扰动，而集中式模型先进行原始数据收集，后进行隐私处理。另外，在本地模型中，D代表一个用户的数据，D′代表同一用户依概率改变后的数据。

Table 1 Difference of the two differential privacy models表1 两种差分隐私模型的差异

而集中式模型的D代表所有用户的数据，D′代表除去有数据变化用户的所有用户数据。

在针对隐私数据分析的本地模型中，每个本地用户用随机器Qi扰乱个人数据vi得到zi，数据收集者将其汇总得到s，最后进行数据分析。本地模型下的数据分析流程如图2所示。

Figure 2 Analysis process under local model图2 本地模型下的数据分析流程

差分隐私的序列组合特性是最常用的隐私预算ε分配策略(并行策略参见文献[15])。

定理1(Laplace机制)[17]函数f：D→Rd，敏感度为Δf，随机算法A(D)=f(D)+Y满足ε-DP，其中Y～Lap(Δf/ε)为随机噪声。

Laplace机制经常被用于本地模型中，常用于对数值型结果的隐私保护(指数机制、几何机制参见文献[15,16])。

2.3 随机应答

随机应答RR(Randomized Response)[28,29]是一种被用来保护敏感话题调查参与者隐私的技术，同时目前主流的本地差分隐私保护机制都是基于随机应答策略的。具体应用场景为：每个人不是属于组A就是组B，问题是在不能确定具体个人属于哪组的前提下，估计组A中人数的比例。随机应答给出的解决方案：随机选取n个人，随机设备(可以是抛硬币、摸球模型)以概率p指向A，以(1-p)指向B。在每轮调查中，受访者只需回答设备指向(调查者未知)的组别是否与其真正的组别一致(Yes或No)，这样便可以得到组A人数π的最大似然估计。其中，P(Xi=1)=πp+(1-π)(1-p)，P(Xi=0)=(1-π)p+π(1-p)，令n1、n-n1分别记为回答Yes和No的人数，则似然估计为L=[πp+(1-π)(1-p)]n1[(1-π)p+π(1-p)]n-n1。易得，当p≠1/2时，π的最大似然估计为:

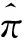
通过RR技术，每个参与者都可以否认“Yes”，因为这个结果基于设备的概率性，这样实现了针对个体的隐私保护。作为一种加强版本，参与者可以进行二次随机应答。若随机设备采用抛硬币方式实现，“Yes”的估计为2(Y-0.25)，其中Y为“Yes”应答比例。重要的是，RR机制满足差分隐私机制，不依赖于攻击者的先验知识，可以在数据收集中保护任一参与者的隐私，参与者可以拥有ε=ln(0.75/(1-0.75))=ln (3) 的隐私保护水平[2,12]。

LDP模型最早由RR技术实现，并应用于Google和Apple公司各自的产品中[2]。现有基于RR技术的LDP机制在数据挖掘中具有一定的局限性，只适用于用户数据类型为数值型或范围型，而数据收集者的数据挖掘任务局限于基本统计，如计数或求中位值等。但是，RR技术及其改进模型在收集群体层面的统计数据而不泄露个体数据方面具有优越性能，目前已成为新的研究热点。

3 主要研究方向

目前针对LDP的研究方向主要涉及基于随机应答与BloomFilter的编解码方式研究、针对流式频繁项集挖掘Heavy Hitters挖掘和针对智能终端的收集与机器学习等。

3.1 针对LDP的随机应答

已经应用于Google的Chrome浏览器的RAPPOR[12]是最早支持本地差分隐私的数据收集和众包数据统计的通用技术，采用随机应答策略和BloomFilter保证在研究用户群体数据时不能窥探到个体的信息，实现了针对客户端群体的类别、频率、直方图和字符串类型统计数据的隐私保护分析。RAPPOR应答被定义为比特位字符串，每一位都是对应用户端特性报告的逻辑谓词随机应答，用来收集用户群体的数值和序数值的统计，可以提供ln (3) 的差分隐私保护。

算法1用户端的RAPPOR算法

输入：用户数据X，参数k(串长度)，h(Hash个数)，概率参数f、p、q。

输出：数据报告s。

(1)信号处理。用h个哈希函数将X映射到大小为k的BloomFilterB上。

(2)永久随机响应(PRR)。每个X与BloomFilterB中的i生成二进制报告B′。

(3)即时随机响应(IRR)。分配一个大小为k的比特串s，初始化为0，依照概率参数设置s中的比特i。

(4)报文。把收集的报告s发送到服务器。

在算法1中，RAPPOR采用两个满足差分隐私的机制：永久和即时的随机应答，不仅可以单独调节隐私保护水平，而且BloomFilter可以增加额外的不确定性，不仅压缩了报文大小，更增加了攻击者的攻击难度。如图3所示，用户数据为X=“Male”，BloomFilterB大小为k=8，哈希函数个数h=3，BloomFilterB产生永久随机响应B′，每次数据收集(如每天)，数据收集者得到即时随机响应X′。由差分隐私保证，最厉害的攻击者最终只能收集到X′，不能推理到X。因为BloomFilter中多个值映射为一个比特位，使针对用户个人的攻击更难实现。

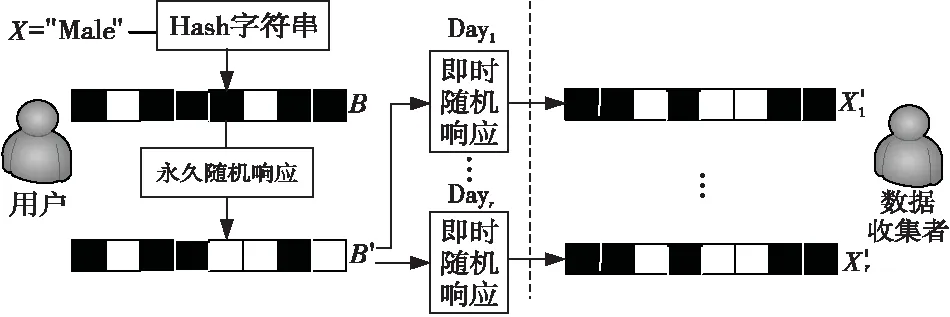
Figure 3 Life-cycle of the RAPPOR图3 RAPPOR报文的生命周期

RAPPOR在解码过程中结合成熟的假设检验、最小二乘求解和LASSO(Least Absolute Shrinkage and Selection Operator)回归[30]实现了针对字符串抽样群体频率的高可用解码框架。然而，RAPPOR的两个假设经常限制其实际应用：(1)使用RAPPOR的数据收集者只能孤立地了解单一变量的分布。实际上，研究多个变量之间的关联是更有意义的，比如，使用浏览器分析多个不相干的主页浏览记录或搜索URL与恶意软件的安装相关性关系。(2)数据收集者必须事先知道潜在字符串字典、安装软件的报告、名称、hash值，然而这些是不可能作为先验知识的。针对以上问题，对未知分布多变量关联分析和学习未知频率分布的用户端字符串可以作为解决方案，同时，构建候选字符串字典并应对大规模数据集的增加依然是制约算法效能的瓶颈，算法的并行化优化和分布式集群扩展可以作为一个有意义的研究方向。

3.2 基于LDP的流式频繁项集挖掘

频繁项集挖掘是数据挖掘领域的一项重要技术，可用于关联规则挖掘、用户行为预测以及相关性分析。而流式频繁项集挖掘主要解决top-k频繁项集任务，现有支持隐私保护的方案中，大量的通信消耗、隐私预算的损耗与可用性的平衡一直是基于LDP的流式频繁项集挖掘难点。针对集值数据(Set-Valued Data)上的流式频繁项集挖掘(Heavy Hitter Mining)任务，卡塔尔大学的于挺教授团队[31]在RAPPOR机制和Succinct Histgram的基础上，提出的LDPMiner方法[4]将挖掘任务分成两个子处理过程，如图4所示。首先，Sampling SH算法完成对流式频繁项的主成分识别工作，从噪声数据中初步确定流式频繁项的选值范围，然后Sampling RAPPOR算法对前一过程的结果进行频数估计上的调优处理，得到相比单一处理过程更为精确的流式频繁项结果。

Figure 4 Framework of the LDPMiner图4 LDPMiner的两阶段框架

3.3 其他成果

John等人[18]在2013年首先提出了Local Differential Privacy(1965年Warner提出的Random Response更早[28])。而苹果的差分隐私技术着眼于整体又保护个体，是唯一一家将Differential Privacy作为标准大规模部署的公司，但不像Google的RAPPOR，其技术一直未开源。苹果在WWDC2016、WWDC2017上倡导的Differetial Privacy和No User Profiling主要涉及三方面[19,20]：

(1)局部抽样：以某一频率局部采集一部分用户的数据，而不是收集用户的整体数据；

(2)Hash加密：用BloomFilter将用户数据做Hash运算，实现在保护用户隐私的前提下，得到用户是否使用某些固定表达的特征；

(3)噪声扰动：在收集用户数据前，先加入随机噪声，只要被注入的噪音抽样是正态分布的，那么整体来看，这些噪音最终将相互抵消。

这也给研究人员提供了避免在全局中暴露采样信息的思路：无需建立User Profile，Group Profile的精度就足够，只要数据量充足，即使只有加噪数据，依然可以获得群体趋势的统计量。总之，相比于效率低的传统密码学技术，苹果、谷歌等公司不断对本地差分隐私技术的商用，给我们对LDP技术的研究带来很大的动力，也希望苹果公司采用的相关技术细节可以早日开源，进一步推动LDP理论研究和实际应用。

本地差分隐私在数据挖掘中的应用研究与差分隐私的理论发展密切相关。对基于LDP的主流算法的总结如表2所示。

Table 2 Comparison among different LDP models表2 主流LDP算法的比较

4 LDP的理论分析

纵观现有文献的研究，LDP技术差分隐私理论分析主要涉及统计分析理论、差分隐私证明等。LDP的差分隐私证明是严格的，尤其基于随机响应的本地隐私差分保护研究很广泛。例如，可证明RAPPOR满足差分隐私的定义。其中，永久随机响应(PRR)保证了来自真值的加噪值保护隐私。

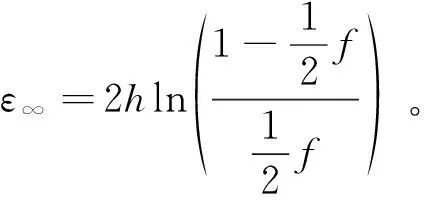
证明S=s1,…，sk是RAPPOR产生的随机报告，在已知用户数据V的条件下，观测任意S的概率，假设永久随机响应B′是已知的。

P(S=s|V=v)=

P(S=s|B,B′,v)·P(B′|B,v)·P(B|v)=

P(S=s|B′)·P(B′|B)·P(B|v)=

P(S=s|B′)·P(B′|B)

对于P(B′|B)相关概率如下：

不失一般性，BloomFilter的比特位1，…，h，设置为，b*={b1=1，…，bh=1，bh+1=0，…，bk=0}，

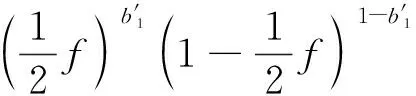
(1)

□

□

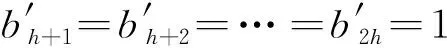
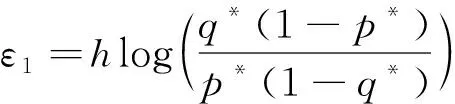
对于N个用户报文，差分隐私考虑输入只差一个记录j(报告集D1和D2只差一个报告Sj)，其他的在比值中约掉。

为第n次数据收集，计算εn需要额外假设攻击在从B′获得信息的效能。N越大，ε∞越小。然而，基于随机响应的差分隐私理论分析依然处于起步阶段，更高级的数理统计分析技术(如多随机变量相关性分析等)的应用将丰富本地差分隐私的理论研究。

5 结束语

随着众包模式的兴起与大数据分析产业的推动，本地差分隐私近年来的研究在理论上不断发展和完善，并在统计学、机器学习、数据挖掘、社交网络等领域得到了初步应用。本文介绍了本地差分隐私保护的基础理论，并着重介绍了主流LDP技术的数据收集与数据分析方法，最后从理论推导的角度对LDP技术进行分析。虽然LDP技术的研究和发展都较传统差分隐私起步晚，仍是一个相对年轻的研究领域，但近年来其在互联网领域的大规模应用给学界和产业界都带来强大动力。对于本地差分隐私保护，在理论和应用上都还存在一些难点以及新的方向需要进一步深入研究，包括：

(1)基于LDP的众包机器学习。

LDP技术源自于众包模式，在支持用户隐私保护的数据收集、支持隐私保护的机器学习、统计分析等领域具有很大的研究前景。国内南京大学网络合作与安全研究中心COSEC(Network Cooperation and Security Research Center)团队在抗大数据分析的隐私保护方法的研究中，提出的一种适用于各种移动感知众包任务的交易平台便是一个很好的探索。然而，分布式条件下的数据同步与集中统计分析是一个不容忽视的技术难点。

(2)抵抗新型攻击的能力方面。

文献[1]中提出的具有隐私保护数据生成能力的生成式对抗网络GAN(Generative Adversarial Networks)，可以针对该网络模型欺骗众包模式下的其他同等用户，这种新型攻击方式需要研究者引起重视。因此，完善本地隐私保护的理论根基，理清隐私保护与攻击就是矛和盾的关系，才能不断完善和提高，使LDP技术提供最可靠的用户隐私保护支持。

(3)差分隐私下的大数据分析。

随着大数据技术的发展，越来越多的应用涉及到大数据，社交网络、微博、医疗信息、生命科学以及定位系统服务等。利用Hadoop、Spark、Storm等大数据分析平台，实现支持差分隐私的数据挖掘和分析，尤其是基于RAPPOR技术的本地隐私保护算法在大规模数据字典的构建与计算效能间的优化亟待解决。

总之，本地差分隐私保护是目前信息安全领域的研究热点之一，也取得了丰富的研究成果。本文从理论和应用的角度对本地差分隐私保护目前的研究状况进行综述，希望能够为该领域的研究者提供有价值的参考信息。

[1] Hitaj B, Ateniese G, Pérez-Cruz F. Deep models under the GAN:Information leakage from collaborative deep learning[C]∥Proc of the 2017 ACM SIGSAC Conference on Computer and Communications Security, 2017:603-618.

[3] Avent B, Korolova A, Zeber D, et al. Blender: Enabling local search with a hybrid differential privacy model[C]∥Proc of the 26th USENIX Security Symposium, 2017: 747-764.

[4] Qin Z, Yang Y, Yu T, et al. Heavy hitter estimation over set-valued data with local differential privacy[C]∥Proc of the 2016 ACM SIGSAC Conference on Computer and Communications Security, 2016:192-203.

[5] Dalenius T.Towards a methodology for statistical disclosure control[J].Statistic Tidskrift,1977,15(2):429-444.

[6] Sweeney L.k-anonymity:A model for protecting privacy[J].International Journal of Uncertainty,Fuzziness and Knowledge-Based Systems,2002,10(5):557-570.

[7] Machanavajjhala A, Gehrke J, Kifer D, et al.l-diversity: Privacy beyondk-anonymity[C]∥ Proc of the 22nd International Conference onData Engineering, 2006: 24.

[8] Li N, Li T, Venkatasubramanian S.t-closeness: Privacy beyondk-anonymity andl-diversity[C]∥Proc of IEEE 23rd International Conference on Data Engineering, 2007:106-115.

[9] Wong R C W, Li J, Fu A W C, et al. (α,k)-anonymity: An enhancedk-anonymity model for privacy preserving data publishing[C]∥Proc of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2006:754-759.

[10] Xiao X, Tao Y. M-invariance:Towards privacy preserving re-publication of dynamic datasets[C]∥Proc of the 2007 ACM SIGMOD International Conference on Management of Data,2007:689-700.

[11] Zhao Y, Du M, Le J, et al.A survey on privacy preserving approaches in data publishing[C]∥Proc of the 1st International Workshop on Database Technology and Applications,2009:128-131.

[12] Erlingsson U, Pihur V, Korolova A. RAPPOR:Randomized aggregatable privacy-preserving ordinal response[C]∥Proc of CCS’14,2014:1054-1067.

[13] Dwork C. A firm foundation for private dataanalysis[J].Communications of the ACM,2011,54(1):86-95.

[14] Dwork C,Krishnaram K,Frank M,et.al.Our data,ourselves:Privacy via distributed noise generation[C]∥Proc of the 25th Annual International Conference on the Theory and Applications of Cryptographic Techniques (EUROCRYPT), 2006:486-503.

[15] Dwork C,Frank M,Kobbi N.Calibrating noise to sensitivity in private data analysis[C]∥Proc of the 3rd Theory of Cryptography Conference (TCC),2006:265-284.

[16] Dwork C, Moni N,Toniann P.Differential privacy under continual observation[C]∥Proc of the 42nd ACM Symposium on Theory of Computing (STOC),2010:715-724.

[17] Dwork C,Moni N,Toniann P.Pan-private streaming algorithms[C]∥Proc of the 1st Symposium on Innovations in Computer Science (ICS),2010:66-80.

[18] John C,Michael I,Martin J.Local privacy and statistical minimax rates[C]∥Proc of the IEEE 54th Annual Symposium on Foundations of Computer Science (FOCS),2013:429-438.

[19] Novac O,Novac M,Gordan C,et al.Comparative study of Google Android,Apple iOS and Microsoft Windows Phone mobile operating systems[C]∥Proc of International Conference on Engineering of Modern Electric Systems, 2017:154-159.

[20] Slva M,Ramos T,Holanda M.Geographic information system with public participat on IoS system[C]∥Proc of the 12th Iberian Conference Information Systems and Technologies,2017:1-5.

[21] Dwork C,Aaron R.The algorithmic foundations of differential privacy[J].Foundations and Trends in Theoretical Computer Science,2014,9(3-4):211-407.

[22] Xu J. Differentially private histogram publication[J].The VLDB Journal,2013,22(6):797-822.

[23] Engel D, Eibl G. Wavelet-based multiresolution smart meter privacy[J].IEEE Transactions on Smart Grid,2017,8(4):1710-1721.

[24] Hay M, Machanavajjhala A, Miklau G, et al. Principled evaluation of differentially private algorithms using dpbench[C]∥Proc of the 2016 International Conference on Management of Data, 2016:139-154.

[25] Nguyên T T, Xiao X, Yang Y, et al.Collecting and analyzing data from smart device users with local differential privacy[J].arXiv preprint arXiv:1606.05053,2016.

[26] KairouzP,Bonawitz K,Ramage D.Discrete distribution estimation under local privacy[C]∥Proc of International Conference on Machine Learning (ICML),2016:2436-2444.

[27] Peter K,Sewoong O,Pramod V.Extremal mechanisms for local differential privacy[J].ar Xivpreprint ar Xiv:1407.1338,2014.

[28] Warner S L. Randomized response:A survey technique for eliminating evasive answer bias[J].Journal of the American Statistical Association,1965,60(309):63-69.

[29] Wikipedia.Randomized response[EB/OL].[2017-06-13].http://en.wikipedia.org/wiki/Randomized_response.

[30] Robert T.Regression shrinkage and selectionvia the Lasso[J].Journal of the Royal Statistical Society,1994,Series B,58:267-288.

[31] Bassily R,Smith A.Local,private,efficient protocols for succinct histograms[C]∥Proc of the 47th ACM Symposium on Theory of Computing (STOC),2015:127-135.