基于随机几何的大规模MIMO中继异构网络性能分析*

周 猛，贾向东,2，颉满刚

(1.西北师范大学计算机科学与工程学院，甘肃 兰州 730070；2.南京邮电大学江苏省无线通信重点实验室，江苏 南京 210003)

1 引言

为了更好地满足大量高端设备对链路的数据请求，同时提供无处不在的用户链接需求，学术界和工业界已经开始了对新一代通信系统即第五代移动通信系统5G(the Fifth-Generation Mobile Communications)的研究，其中，大规模多输入多输出MIMO(massive Multiple-Input Multiple-Output)和异构网络HetNets(Heterogeneous Network)能够极大地提高系统的能量效率EE(Energy Efficiency)和频谱效率SE(Spectral Efficiency)，因此，被业界认为是5G的核心技术[1，2]。

大规模MIMO是对当前传统的MIMO系统放大了多个数量级，即数百根基站天线同时使用同一时频资源，且为数以百计的用户同时提供链接服务[3]，这将极大地提高系统的资源使用率。信道传播条件将成为大规模MIMO系统部署的一个关键因素[4]，在良好的信道传输条件下，通过简单的线性预处理方案诸如最大比结合/最大比传输MRC/MRT(Maximum Ratio Combining/Maximum Ratio Transmission)和迫零ZF(Zero-Forcing)，可以使得用户间干扰、小尺度衰落和加性噪声等不利因素得到有效的遏制，此将使得系统获得更多的信道容量，因此能极大地提高系统的SE和EE。另外，为了支持移动数据快速增长的需求，稠密的小小区也将被期望部署到未来的5G蜂窝移动通信网络中，这就导致了HetNets的出现[5 - 7]。在多层的混合异构蜂窝网络中，宏基站主要用于用户的调度和资源的分配，同时还要满足高移动性用户的需求，而稠密的小小区基站则主要是为了向低移动性的用户提供较高服务质量的链路请求。

文献[8]指出，超密集网络和大规模MIMO技术能够为系统带来极大的频谱效率和空间复用增益，因而能够极大地提高系统的信道容量。尽管很多文献已经在HetNets和大规模MIMO方面做出了卓越的贡献，尤其是通过最优化的方法分析了小区间用户的干扰等问题。但是，当前对于大规模MIMO覆盖范围、用户间干扰和数据链路速率等问题在异构蜂窝网络中却没有得到相应的研究。近来文献[9]指出，使用随机几何方法可以有效地解决此问题。基于此，文献[10]对大规模MIMO系统的正交和非正交两种导频序列情况进行了分析。文献[11]中指出，为了满足大规模MIMO中继系统覆盖范围的要求，部署基站的密度应该有一个确定的下界。不同于文献[11]，文献[12]中对大规模MIMO混合异构网的覆盖概率、性能增益和SE进行了分析。

尽管文献[11-13]都使用了随机几何方法对大规模MIMO系统进行了分析，但其仅限于单层的蜂窝系统，而仅有文献[12,13]采用随机几何方法对混合异构网络进行分析。显然，采用随机几何方法对大规模MIMO 异构蜂窝系统的研究还不够成熟，有很多关键的问题还亟待解决。然而，尽管中继系统已经得到了广泛的研究[14]，但是对基于大规模MIMO中继混合异构网络的随机几何方法尚没有被广泛地研究。

受上文启发，假设系统工作在半双工状态且采用时分双工TDD(Time Division Duplexing)模式，本文采用随机几何方法，对基于放大转发AF(Amplify-and-Forward)的大规模MIMO两层混合异构中继系统的SE进行了研究。其中，MRC/MRT和ZF两种预处理方案被分别部署在大规模MIMO基站。本文首先计算了用户对的信干比SINR(Signal-to-Interference Noise Ratios)和功率放大因子表达式；然后通过随机几何方法，获得了小区总的频谱效率。研究发现，只有当小小区半径小于宏小区保护半径时，系统才能达到最优(或次优)的性能。而对于宏小区的保护半径则存在上界，仅当满足此条件时，增大宏小区的保护半径才有助于提高系统的SE。与此同时，研究同时表明，宏小区半径存在最优的下限，且当宏小区半径小于最优下限时，系统所实现的总的频谱效率随着宏小区半径的增加而增大，且在相同的条件下，ZF能比MRC/MRT预处理方案实现更高的系统性能。

2 系统模型

2.1 两层混合异构网络模型

本文研究了如图1所示的两层大规模MIMO中继异构网络，其中第一层为宏小区MCs(Macro Cells)，第二层为小小区SCs(Small Cells)。假设系统中有B个MCs，其被稠密的SCs所覆盖。每个宏基站MBSs(Macro Base Stations)中都配置了N根天线用来为宏用户MUs(Macro Users)提供服务。同时，为了降低系统的能量损耗，小小区基站SBSs(Small cell Base Station)、小小区用户SUs(Small Users) 和MUs都仅配置了单根天线。其中，MBSs提供基本的覆盖，而SBSs用于提高系统的性能。同时，假定MBSs位于六边形小区的中心，为了分析方便，通常将六边形区域看作圆形区域。MUs均匀地分布在MCs中(除了保护半径外)，其服从密度为λM的泊松点过程PPPs(Poisson Point Processes)。假定每个SCs服从密度为λSC的PPPs，且只有一个SU随机地分布在SCs中，由于SCs和SUs服从相同的分布，根据PPPs的性质，即满足λS=λSC。本文分别用RM、RG和RS表示MCs半径、MCs的保护半径和SCs半径。

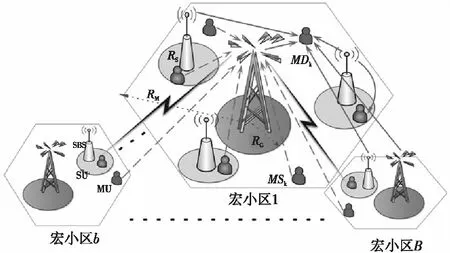
Figure 1 Two-tier HetNets with massive MIMO relay图1 两层大规模MIMO中继混合异构网络

2.2 多对宏用户对目标小区基站的信号传输

假定MC1为目标研究小区，其中宏基站MBS1用来协助KM1宏用户对之间的链路通信，(MSk,MDk),k=1,2,…,KM1。假定由于严重的路径损耗和几何衰减对系统的影响，任何宏用户对(MSk,MDk)必须在基站BS(Base Station)的协助下才能进行链路的通信。同时,假设系统采用时分双工TDD网络通信模式，当SCs进行上行链路通信时，MCs也进行相同方向的链路通信，且两层网络共享相同的频带。在目标MC1中，KM1用户对(MSk,MDk)之间的链路分为两个阶段，在上行阶段，MBS1接收到的信号为:

(1)

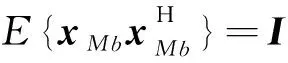
(2)

与此同时，表示从b-th MCs中k-th SU到MBS1中n-th天线的信道系数ωSbkn可表示为:

(3)

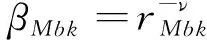
在下行阶段，由于系统采用放大转发AF协议，基站MBS1将接收到的从信源MSk发送的信号经过预处理后，将yT=ρFyR转发到信宿MDk。由于MUs、SUs和SCs均服从PPPs，因此功率放大因子ρ可表示为:

(4)

(5)

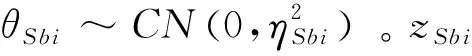
(6)

其中，hMbkn代表小规模衰落系数且满足hMbkn～CN(0,1)。αMbk代表由路径损耗指数v和MBS1到信宿MDk的距离所决定的大规模衰落。根据式(5)信宿所接收到的信号yDk，信宿MDk的SINR为:

(7)

其中，定义NT1为:

(8)

3 系统所实现的各态历经速率

由文献[13]可知，目标小区所得到的总的频谱效率为:

RM1=

(9)

其中，随机变量κ代表MCs1中MUs的平均个数，1/2是由于通信需要进行上/下行两个阶段。由式(9)可知，为了得到RM1的近似值，用户对(MSk,MDk)的条件概率必须首先给出，即:

(10)

其中，γDk由式(7)定义。通常，由式(7)和式(10)是很难直接得到RM1k的。利用凸函数和Jenson不等式的性质，RM1k的下界可以表示为:

(11)

其中，定义EγDk=E(1/γDk)。以下两部分分别采用MRC/MRT和ZF两种预处理方案来计算ρ2(或1/ρ2)和EγDk。

3.1 MRC/MRT预处理方案

当MRC/MRT方案部署在大规模MIMO中继系统时，由文献[15]可知，预处理矩阵F可以表示为:

(12)

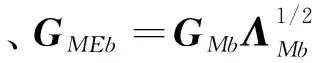
(13)

(14)

同理，式(4)中分母中第一项和第三项可分别表示为:

(15)

(16)

(17)

综合式(14)～式(17)，对于两层混合异构网络，当MRC/MRT预处理方案部署在大规模MIMO放大转发中继系统时，功率放大因子ρ可以表示为:

(18)

其中，μM、CGM、CSG分别定义为：

(19)

定理1当MRC/MRT预处理方案部署在大规模MIMO中继系统时，对于特定目标小区，其系统所实现的各态历经速率RM1_L_Bound可以近似地表示为：

(20)

其中，1/ρ2由式(18)给出，此外，式(20)的证明可参考附录A，NT2由式(32)定义。

3.2 ZF预处理方案

当ZF预处理方案部署在大规模MIMO中继系统时，预处理矩阵F[16]可以表示成：

(21)

(22)

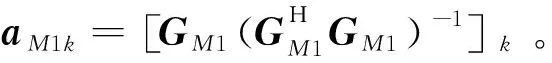
(23)

其中，NT1由式(8)定义。

由式(4)可得，1/ρ2可以表示为：

(24)

考虑到式(24)中，等号右侧的四部分具有相似的形式，现分析第二项。根据式(21)，则：

(25)

(26)

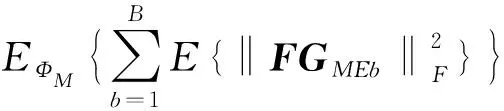
(27)

同式(25)～式(27)的分析，因此式(24)可以进一步如下表示：

(28)

定理2当ZF预处理方案部署在大规模MIMO中继系统时，在目标小区中所获得系统总的频谱效率可以近似地表示为：

(29)

其中，1/ρ2由式(28)定义，此外，式(29)的证明可参考附录B。

4 数值与仿真分析

基于以上分析，此节对基于MRC/MRT和ZF两种预处理方案下所实现的频谱效率进行数值仿真。假设λS=6×10-4m-2，路径损耗指数ν=4。

设定RM=1 000 m，RG=20 m，RS=20 m，本文首先在图2a和图2b分别给出了两种不同预处理方案下系统所实现的总SE与MUs的关系，也分别考虑了不同数量基站天线对系统实现SE的影响。通过对图2a和图2b的比较发现，对于给定的RM，系统所实现的SE随着MBS天线数量的增加而增大。这是因为，越多的基站天线可以为系统带来越多的天线增益。研究同时发现，对于给定的RM和N，当μM相对较小时，对于特定小区中，随着MUs的μM的增加系统SE逐渐增大。这是由于所有的MUs共享相同的时频资源，能够为系统带来更高的频谱复用增益，因此能够明显地改善系统的SE。图2b中对MRC/MRT和ZF两种预处理方案所实现的SE进行了比较，研究发现，在相同的条件下，ZF比MRC/MRT预处理方案的系统性能更好。

Figure 2 Aggregate SE of MUs in the object cell图2 目标小区所实现总的频谱效率

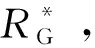
Figure 3 Impact of RG and RS on aggregate SE (RM=1 000 m, μM=10,N=1 000)图3 RG和RS对频谱效率的影响(RM=1 000 m,μM=10,N=1 000)

Figure 4 Joint impact of network parameters RM, RS,and RG on aggregate SE (μM=50,N=1 000)图4 RM、RS、和RG对频谱效率的联合影响 (μM=50,N=1 000)

假定μM=50，N=1 000，图4分别给出了RM、RG、RS对系统的SE影响。图4a中，设定RG=20 m,RS=10 m,20 m,25 m,30 m，图4b中，RS=20 m,RG=10 m,20 m,40 m,80 m,100 m。当RS>RG时，图4a表明系统的SE随着RS的增大而减小，这是由于RS的增大，小区内严重的SUs干扰降低了系统总的SE。与此同时，图4表明，当RM相对较小时，增大RG将极大地改善系统的SE,而且增加RM也能够提高系统的SE。然而，当RM足够大时，系统所实现的SE将达到一个定值，但却随着RS而改变。从图4a中发现，ZF方案优于MRC/MRT。

此外，图4b给出了保护半径RG对系统SE的影响。研究首先表明，当RG≤RS时，越小的保护半径RG，将导致越低的SE，这是由于SUs对系统所造成的严重干扰；其次，当RG>RS时，且RM相对较小时，保护半径RG将对系统SE有严重的影响。当然，对于MRC/MRT和ZF两种不同的预处理，系统所实现的渐近定值是不相同的。特别地，对于不同的RM，很容易发现，保护半径RG对总的SE有严重的影响。

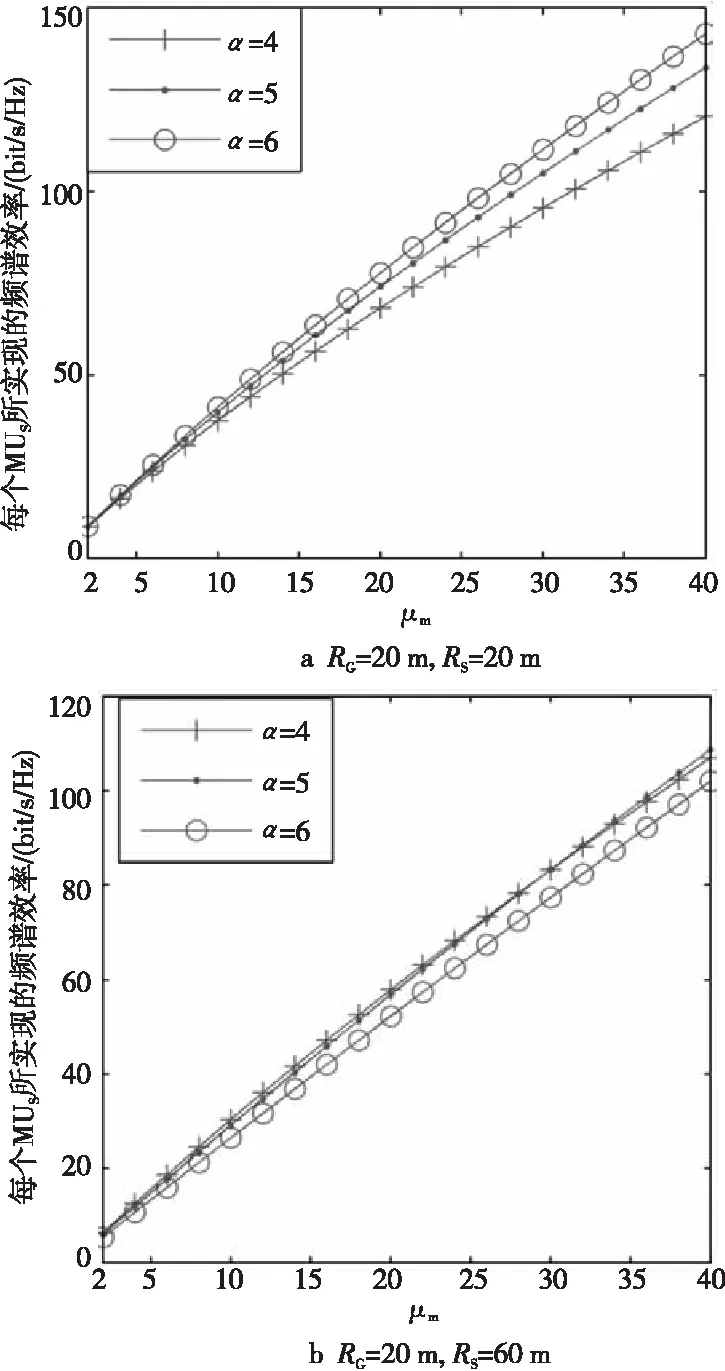
Figure 5 Impact of path loss exponent ν(MRC/MRT)图5 路径损耗指数ν的影响(MRC/MRT)

图5描述了路径损耗指数和小区中MUs的数量μM对系统SE的影响。通过对图5a和图5b的比较发现，路径损耗指数ν对SE的影响依赖于RG和RS。特别地，当RSRG)较小时，系统所实现的SE随着ν的降低而减小。尽管如此，研究发现，越大的小区半径RS，造成的性能损失越大，其主要原因是当RS-RG(RS>RG)较小时，来自宏小区用户的干扰大于小小区的用户。而这些从SUs的干扰可以被忽略，以至于MUs的干扰成为导致性能损失的主要因素。这种情况下，提高期望信号的发送功率可以降低由于增大路径损耗指数ν所造成的影响。然而，当RS-RG逐渐增大时，SUs引起的干扰大于MUs引起的干扰，以至于SUs成为造成干扰的主要因素。

5 结束语

基于随机几何方法，本文分别研究了MRC/MRT和ZF预处理方案下的双层大规模MIMO中继异构网络系统所实现的频谱效率，特别地，得出了实现总频谱效率的闭式解。系统仿真结果表明，相同的系统参数条件下，ZF预处理方案优于MRC/MRT方案。同时研究发现，实现的各态历经速率受到MBS天线数量、RM、RS、RG以及宏小区中MUs数量等系统参数的影响。通常，系统所实现的频谱效率随着MUs数量的增加而增大，然而，当小区中平均MUs的数量足够大时，实现的各态历经速率将保持在一个稳定的值。研究同时发现，为了减小宏基站所造成的严重干扰，RS应该小于RM。对于RM的影响，本文发现，当RM相对较小时，系统实现总的频谱效率随着RM的增加而增大。相反，其对系统的各态历经速率的影响将变得很小，即增大RM不能够有效地改善系统的频谱效率。研究的结果有助于两层全双工大规模MIMO中继混合异构系统网络的设计。

[36]Royal Government of Cambodia,“Political Platform of Royal Government of Cambodia of the Fifth Legislature of National Assembly”, https://www.cambodianembassy.org.uk/f_home/PDF/Political_Platform_Royal_Government_Cambodia_5th.pdf, 2013年9月。

附录A

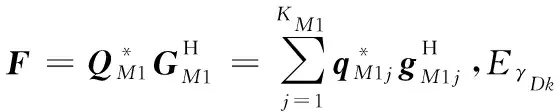
(30)

由于SUs和SCs服从独立同分布，即满足λM=λS。结合式(14)～式(17)，EγDk的闭式表达式可以表示为:

(31)

其中，定义NT2为:

(32)

结合式(11)、式(31)及式(32)，即可完成公式(20)的证明。

附录B

为了得到EγDk的估计值，将式(23)的SINR代入到EγDk中，因此EγDk可以进一步表示为:

(33)

(34)

(35)

(36)

同样地，可以得到E2:

(37)

(38)

由于:

(39)

因此，当ZF预处理方案部署在大规模MIMO基站时，EγDk可以表示为:

(40)

其中，1/ρ2和NT2分别由式(28)和式(32)给出。因此，结合式(11)及式(40)，即可完成式(20)的证明。

[1] Andrews J G,Buzzi S,Choi W,et al.What will 5G be ?[J].IEEE Journal on Selected Areas in Communications,2014,32(6):1065-1082.

[2] You Xiao-hu, Pan Zhi-wen,Gao Xi-qi,et al.The 5G mobile communication:The development trends and its emerging key techniques[J].Science China-Information Sciences,2014,44(5):551-563.(in Chinese)

[3] Larsson E G,Edfors O,Tufvesson F,et al.Massive MIMO for next generation wireless systems[J].IEEE Communications Magazine,2014,52(2):186-195.

[4] Ngo H Q,Larsson E G,Marzetta T L.Aspects of favorable propagation in massive MIMO[C]∥Proc of the European Signal Processing Conference,2014:76-80.

[5] Kamel M,Hamouda W,Youssef A.Ultra-dense networks:A survey[J].IEEE Communications Surveys & Tutorials,2017,18(4):2522-2545.

[6] Xie Man-gang,Jia Xiang-dong,Zhou Meng,et al. User-pair association scheme for multi-tier relay cooperative HetNets[J].Computer Engineering,2017,43(9):133-137.(in Chinese)

[7] Sanguinetti L,Moustakas A L,Debbah M.Interference management in 5G reverse TDD HetNets with wireless backhaul:A large system analysis[J].IEEE Journal on Selected Areas in Communications,2015,33(6):1187-1200.

[8] Gotsis A G,Stefanatos S,Alexiou A.Optimal user association for massive MIMO empowered ultra-dense wireless networks[C]∥Proc of the IEEE International Conference on Communication Workshop (ICCW),2015:2238-2244.

[9] Stoyan D,Kendall W S,Mecke J.Stochastic geometry and its applications[M].2nd Edition.New York:John Wiley & Sons,2013.

[10] Madhusudhanan P,Li Xing,Liu You-jian,et al.Stochastic geometric modeling and interference analysis for massive MIMO systems[C]∥Proc of the International Symposium on Modeling & Optimization in Mobile,2013:15-22.

[11] Zou Xun,Cui Gao-feng,Tang Ming-huan,et al.Base station density bounded by maximum outage probability in massive MIMO system[C]∥Proc of the IEEE Vehicular Technology

Conference,2015:1-5.

[12] Kountouris M,Pappas N.HetNets and massive MIMO:Modeling,potential gains,and performance analysis[C]∥Proc of the IEEE-APS Topical Conference on Antennas and Propagation in Wireless Communications,2013:1319-1322.

[13] Liu Wen,Jin Shi,Wen Chao-kai,et al.A tractable approach to uplink spectral efficiency of two-tier massive MIMO cellular HetNets[J].IEEE Communications Letters,2016,20(2):348-351.

[14] Haenggi M,Ganti R K.Interference in large wireless networks[J].Foundations & Trends® in Networking,2009,3(2):127-248.

[15] Suraweera H A,Ngo H Q,Duong T Q,et al.Multi-pair amplify-and-forward relaying with very large antenna arrays[C]∥Proc of the IEEE International Conference on Communications (ICC),2013:4635-4640.

[16] Zhang Qi,Zhu Hong-bo.Uplink supportive number of users in massive MIMO systems with ZF receivers[J].Journal of Nanjing University of Posts and Telecommunications (Natural Science Edition),2015,35(1):47-51.(in Chinese)

[17] Lee C H,Haenggi M.Interference and outage in poisson cognitive networks[J].IEEE Transactions on Wireless Communications,2012,11(4):1392-1401.

附中文参考文献：

[2] 尤肖虎,潘志文,高西奇,等.5G移动通信发展趋势与若干关键技术[J].中国科学:信息科学,2014,44(5):551-563.

[6] 颉满刚,贾向东,周猛,等.多层中继协助HetNets用户对关联方案[J].计算机工程，2017,43(9):133-137.

[16] 张琦,朱洪波.采用迫零接收机的大规模MIMO上行链路支持用户数研究[J].南京邮电大学学报(自然科学版),2015,35(1):47-51.