SCADA中历史数据的SDT算法研究与改进*

徐旭东，付艳萍

(北京工业大学信息学部计算机学院， 北京 100124)

1 引言

数据采集与监视控制SCADA(Supervisory Control And Data Acquisition)系统是基于组态化软件的流程工业系统，通过对工业设备的实时检测和控制来实现过程数据实时采集和存储、设备的参数设置、警告信号的实时显示等各种功能。

随着物联网和云存储技术的快速发展，R-TU(R-emote Terminal Unit)采集的数据量越来越大，采集周期也越来越短。历史数据库是SCADA系统的重要组成部分，不断地存储系统的历史数据，它可以用于系统故障预测和分析，保证SCADA系统的运行安全和稳定。SCADA中海量的历史数据给数据存储和数据处理造成了极大的负担，高效的数据压缩技术可以节省存储空间，提高存储空间的利用率。为了减少数据传输和永久存储时的开销，在SCADA系统存储数据时采用数据压缩技术是十分必要的[1]。

工业中数据压缩的方法一般有两种：无损压缩和有损压缩。无损压缩是指压缩前和压缩后的数据完全一致；而有损压缩是指解压缩后的数据与原来的数据有一定的误差，但是不影响数据的变化趋势。SCADA系统中常用的数据压缩方法有三种：分段线性方法、矢量量化方法和信号变换法。分段线性方法又包括矩形波串法(Box Car)、向后斜率法(Back Slope)、SDT(Swing Door Trending)以及PLOT(Piecewise Linear Online Trending)。矩形波串法和向后斜率法在数据变化缓慢的情况下数据压缩效果不明显，为解决这一问题，SDT和PLOT应运而生[2]。在很多流程工业中，矩形波串法和向后斜率法二者结合形成的BCBS(Box Car Back Slope)也一直在使用[3]。

在数据压缩算法中，有三个关键点：第一，由于硬件资源的限制和需要存储的数据量越来越多，所以压缩算法需要高压缩比；第二，在SCADA数据库中，数据的查询和存储要求的时间比较短，这要求压缩算法的压缩和解压缩的速度要快；第三，为了保证解压缩后的数据能够准确地描述数据的增长趋势，压缩算法的压缩精度要高、压缩误差要低。一般说来，同时满足高压缩比、低压缩误差、压缩时间短是不可能的，为了达到一个好的压缩效果，需要在三者之间找到一个平衡点[4]。

SDT算法在流程工业中用得最多，具有算法简单、操作容易、执行速度快的优点。信号变换方法也有很多，例如离散余弦变换、小波变换，现如今小波变换的应用领域十分广泛，但相对于SDT算法来说，算法的复杂程度较高。

2 SCADA历史数据压缩策略

SCADA系统中的历史数据主要包括：(1)遥控信息(状态量)：包括各种控制命令；(2)遥信信息(状态量)：包括各种开关状态信息；(3)遥测信息模拟量：主要包括温度、湿度等实时数据信息。

2.1 状态量的压缩

状态量信号的值只有0和1两个数值，采集模块以固定的时间间隔采集，在实际过程中，状态量数据在一段时间内不会发生变化，会出现当前采集的状态信号和上一时刻采集的状态信号是一致的。对于状态量的压缩，我们可以采用逢变则存的处理方法，即状态量的数值发生变化时才需要保存。如图1所示，时间点t0～t7的状态量值分别为1,0,0,1,0,0,0,0，根据状态量的压缩思想，只会保存t0、t3时刻的状态量值，其余时刻的状态量值不保存。

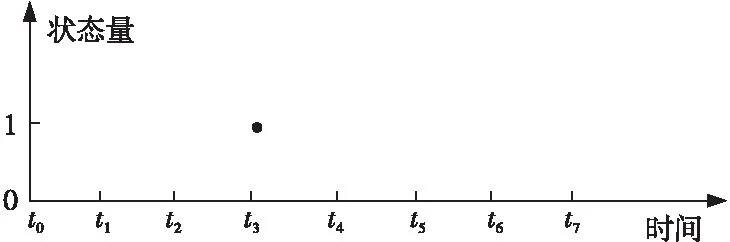
Figure 1 Compressing of state variables图1 状态量的压缩

2.2 模拟量的压缩

对于SCADA系统中模拟量的压缩一般采用有损压缩，这是因为SCADA系统没有必要记录每一个时间点上的模拟量值，只需要记录一段时间数据的变化趋势和异常点。有损压缩方法中SDT算法是一种基于线性拟合的数据压缩方法，它尽可能地延长直线趋势，允许数据在最大的误差范围，尽量减少计算量[5]。

SDT算法是由Bristol在1990年提出的，它通过不断构造平行四边形来选择保存的数据，对于落在平行四边形内的数据不予保存，只存储平行四边形以外的数据[6]。SDT算法的基本步骤如图2所示。

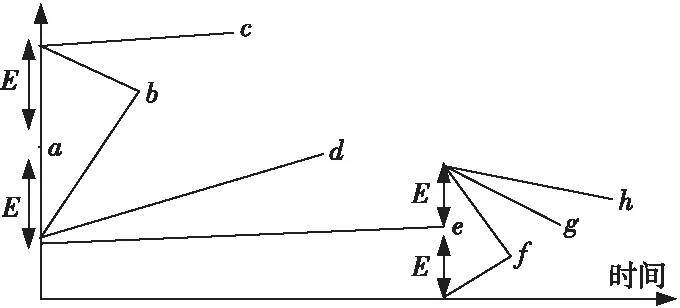
Figure 2 Basic steps of the SDT algorithm图2 SDT算法的基本步骤

设图2中点a为第一个压缩段的第一个数据点，在距离点a为E(也称为门限值)的坐标处各有两个支点，上支点与数据点连线构成最大斜率，下支点与数据点连线构成最小斜率。当只有一个数据点时，上、下支点和数据点在一条直线上，也就是斜率为0，表示旋转门是关闭的；随着数据点越来越多，门将逐步打开，斜率也在不断变化，并且上支点门保持最大斜率，下支点门保持最小斜率。在一段时间内，门一旦打开就不能关闭，直到上支点门和下支点门的斜率一致。只要两扇门未达到平行，或者两个内角之和小于180度，旋转门操作将继续进行。图2中第1个压缩段是从a到d，用a点到d点之间的直线代替数据点(a,b,c,d)；同理，第2个压缩段从e点开始，e点到h点之间的直线代替数据点(e,f,g,h)。

从SDT算法的基本思路可以看出算法存在的一些问题：第一，门限值E是唯一的可控参数，E值的选取直接影响着压缩性能，而且一旦E值确定，在整个压缩过程中是不能改变的。E值的选取一般是根据经验所得，如果选取不合适，将大大降低SDT算法的性能。第二，如果某时间段的数据变化很慢则会导致一轮数据压缩时间过长，就失去了线性趋势的实时性。第三，大多数情况下数据的变化趋势并不是线性的，而SDT算法是用线性趋势拟合数据。第四，SDT算法不处理噪声和野点，会把它当作正常数据，这不仅会降低算法的压缩比，也会影响算法的压缩精度。

3 改进的SDT算法ASDT

针对上述问题，研究者也都提出了改进方法，比如，王举等[7]针对原始算法门限值E不能改变的缺点，提出将给定的初始门限值根据数据的波动情况调整E的大小；于松涛等[8]提出了容差动态调整的思想，根据容差的大小动态设置门限值；曲奕霖等[9]采用反馈控制系统模型，实现了容差在压缩过程的动态变化；张景涛等[10]提出数据压缩的性能在很大程度上取决于压缩偏差，在数据压缩过程中应该动态选取压缩偏差参数的方法；段培永等[11]提出不能简单地用一条直线的斜率来表示一段数据的变化趋势，保存的数据点都是由计算得到的，而不是被压缩数据中的点；宁海楠[12]提出了一种新的过程数据压缩算法NSDT(New Swing Door Trending ),采用抛物线对过程数据的变化趋势进行拟合来实现数据压缩；张健等[13]提出要检测和去除异常点，设定记录限的长度等等。

以上改进算法都存在一些不足之处。第一，都是针对SDT算法存在的问题的一方面提出解决办法，没有综合考虑所有问题来提出解决方案。第二，采用直线对压缩数据进行拟合，也有提出采用曲线拟合压缩数据，但是根据函数的单调性的判定方法，在一段区间上曲线是单调递增或单调递减的。在实际情况中，数据的变化在一段时间内不可能是一直递增或递减的，不能从根本上改变数据的变化趋势。第三，改进的算法中有提出设定强制记录限FSRL(Forced Storage Recording Limit)来解决一轮的压缩时间过长的问题，这无疑增加了算法的复杂性[14]。第四，改进算法大都没有考虑处理异常点和野点。在数据压缩过程中，有的数据和其他的数据相差甚远，这些数据点为异常点。在SCADA系统中，异常数据的出现代表着系统可能出现故障，对于系统的正常运行有着重要的意义。野点和异常点一样都会影响数据压缩算法的压缩精度，降低数据压缩算法的性能。因此，在数据压缩算法中处理异常点和野点是十分有必要的。

本文提出的改进SDT算法ASDT(Advanced Swing Door Trending)通过正弦曲线拟合数据，在一个周期内，数据的变化有增有减，符合数据的变化规律。针对SDT算法存在的问题，ASDT算法可以根据正弦曲线的特点来解决。首先，ASDT算法可以利用正弦曲线的周期性，将一个压缩区间的长度限定在一个周期；其次，将正弦周期的第一个数据和门限值E一起作为ASDT算法的调节参数，由于正弦周期的第一个数据不是固定的，所以现在的调节参数就不是固定不变的，可以达到一个动态调整门限值的效果；最后，ASDT算法会处理异常点和野点，对于异常点的处理：设置记录值上限RL，如果数据超出记录值上限，则保存此数据。对于野点的处理：可以设置一个临界值NL，如果一个数据与其相邻点的数据之差大于NL，则这个数据是野点，可以忽略不计。

对于正弦曲线周期的设定，不仅要考虑压缩区间的长度，还要考虑流程工业压缩比问题。流程工业一般都采用10∶1的压缩比，如果超过此数据，会丢失一些有用的细节，正弦曲线的一个周期将作为一个压缩区间，所以将周期设为10，既限定了压缩区间长度又保证了压缩比。图3为ASDT算法的流程图，在ASDT算法中，TL为压缩区间的长度，RL为记录值上限，NL为野点临界值，每个正弦周期的第一个数据为A0，一个正弦周期的数值都以A0为基准数据，在A0附近波动，Emax为上限值，Emin为下限值。

Emax=A0+max(sin(ωt+φ)+E)

Emin=A0+max(sin(ωt+φ)-E)

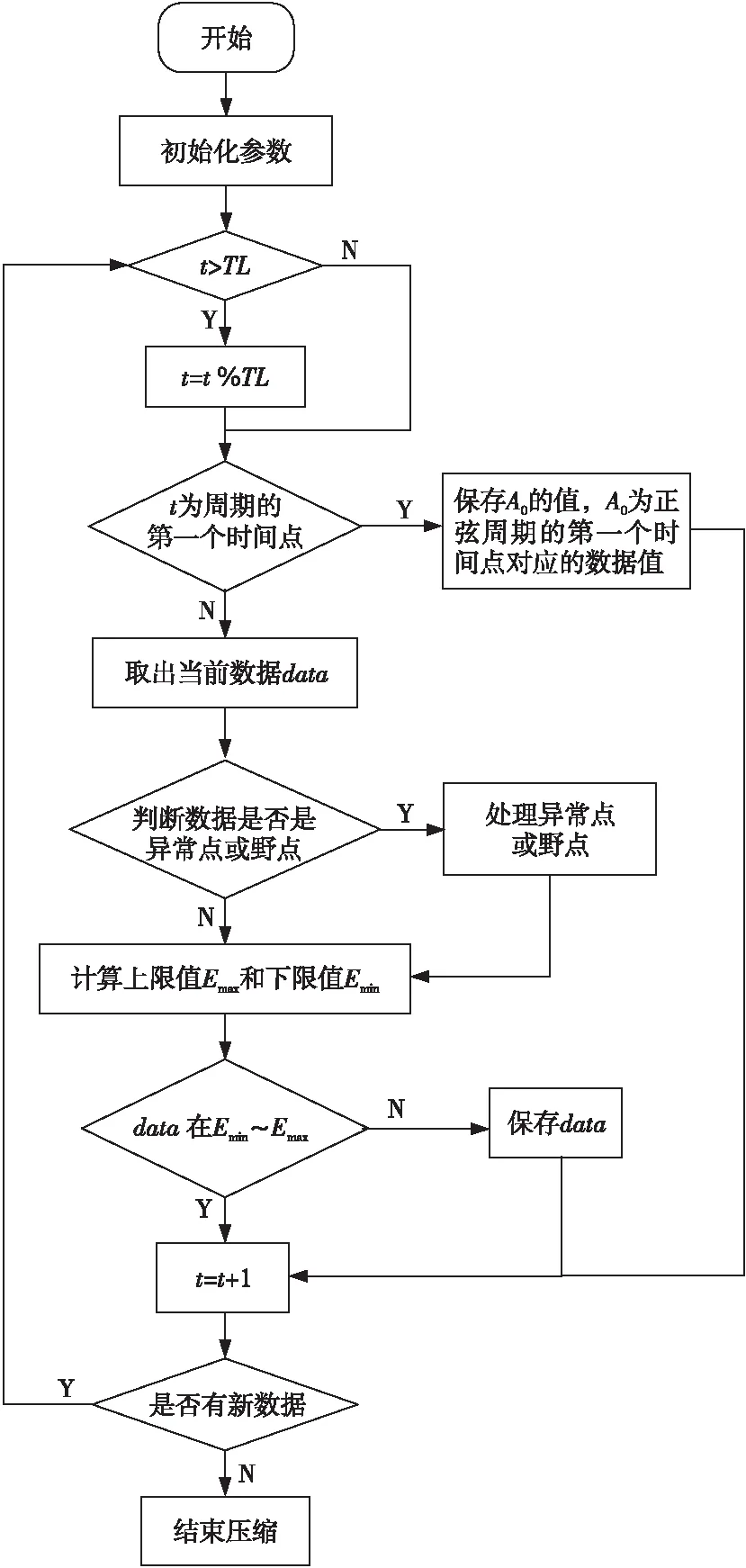
Figure 3 Flow chart of the ASDT algorithm图3 ASDT算法流程图

ASDT算法的具体步骤如下：

步骤1参数的初始化，TL和T都设置为10，ω=2π/T=2π/10=π/5。

步骤2判断t是否大于TL，如果值为否，转到步骤4。

步骤3对t的值进行处理，t=t%TL。

步骤4判断t是否为正弦周期的第一个时间点,即判断t是否为1，如果是，转到步骤8。

步骤5取出当前数据data的值，判断data是否是异常点或野点，如果是则处理。

步骤6计算上限值Emax、下限值Emin。在一个周期为10的正弦周期内，t分别为2.5和7.5时取得周期的最大值和最小值。

步骤7判断data是否在下限值～上限值的范围内，如果不在此范围内，则保存data的值;否则转到步骤9。

步骤8保存A0的值，为正弦周期的第一个时间点对应的数据值。

步骤9t=t+1。

步骤10判断是否有新数据，如果是，转到步骤2。

步骤11结束本次数据压缩。

4 实验结果分析

从算法设计的角度分析，衡量一个算法的好坏,主要是考虑时间复杂度和空间复杂度，简单地说是算法运行所需要的时间和所占的空间。在实际情况中，我们以数据压缩算法所需的压缩时间、解压缩时间以及数据文件所占的空间大小作为衡量压缩算法优劣的标准。NSDT算法也是通过曲线来拟合数据的，所以它和ASDT算法之间的比较更具有可比性。SDT算法、ASDT算法以及NSDT算法所需的时间与空间比较如表1所示。

Table 1 Comparison of storage space and time among SDT, ASDT and NSDT algorithms表1 SDT算法、ASDT算法和NSDT算法时间、空间比较

CR衡量算法的压缩能力，AE、RE、SE、MSE均可衡量数据的失真程度。AE、RE、SE表示整体数据的误差，没有对单个数据的误差进行评价。因此，本实验以MSE作为算法性能分析的指标。

实验的测试数据为SCADA系统的遥测温度值，选取了4组数据，数据量分别为1 000,5 000,10 000,50 000。

图4为SDT算法、ASDT算法和NSDT算法的压缩比比较，图5为SDT算法、ASDT算法和NSDT算法的压缩误差比较，表2为实验的结果数据。

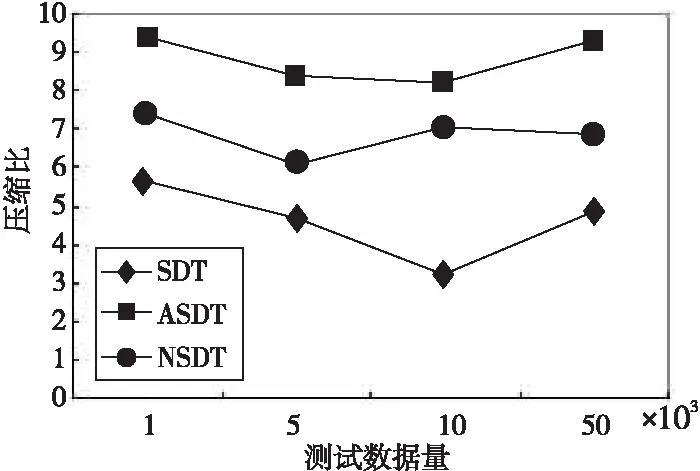
Figure 4 Comparison of compression ratio among SDT,ASDT and NSDT图4 SDT算法、ASDT算法和NSDT算法压缩比比较

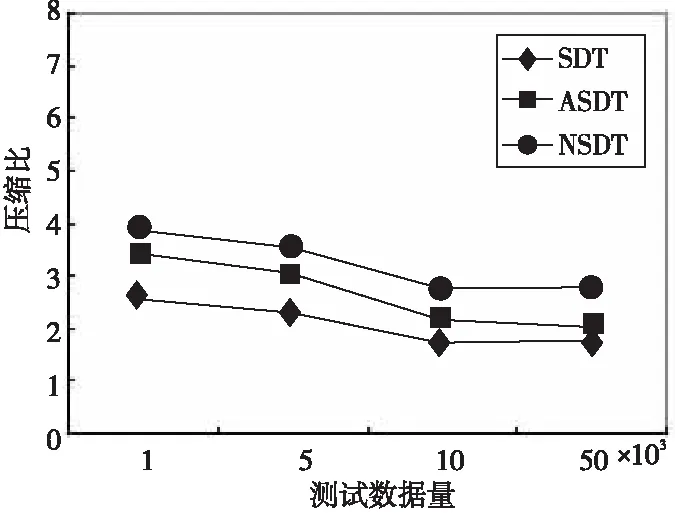
Figure 5 Comparison of compression deviation among SDT, ASDT and NSDT图5 SDT算法、ASDT算法和NSDT算法压缩误差比较Table 2 Performance comparison among SDT, ASDT and NSDT algorithms表2 SDT算法、ASDT算法和NSDT算法性能比较

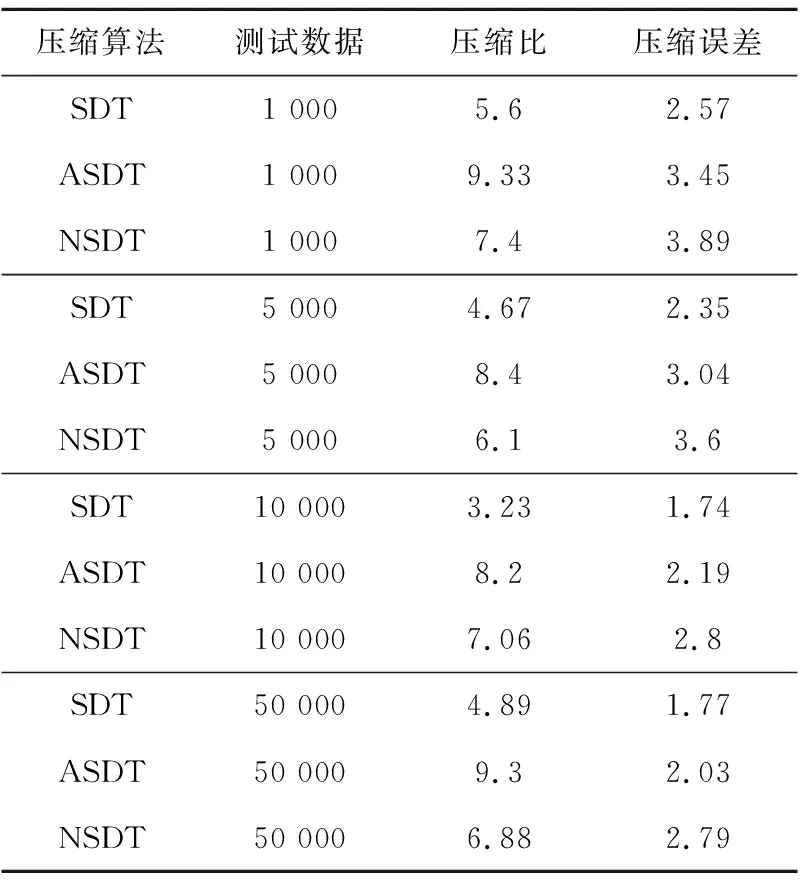
压缩算法测试数据压缩比压缩误差SDT1 0005.62.57ASDT1 0009.333.45NSDT1 0007.43.89SDT5 0004.672.35ASDT5 0008.43.04NSDT5 0006.13.6SDT10 0003.231.74ASDT10 0008.22.19NSDT10 0007.062.8SDT50 0004.891.77ASDT50 0009.32.03NSDT50 0006.882.79

5 结束语

本文提出了一种基于旋转门压缩算法的改进算法ASDT，并编写了程序对测试数据进行模拟计算。ASDT算法不仅解决了传统的旋转门算法直线拟合数据时没有考虑数据在采集过程的实际变化等问题，而且也不需要设定压缩区间的长度。通过上述实验，将SDT算法、ASDT算法以及NSDT算法进行了性能对比，结果表明ASDT算法能在不显著增加压缩误差的前提下，有效地提高压缩比。

[1] Sivalingam S,Hovd M.Effect of data compression on controller performance monitoring[C]∥Proc of 2011 19th Mediterranean Conference on Control & Automation, 2011:594-599.

[2] Vedam H, Venkatasubramanian V,Bhalodia M.A B-spline based method for data compression,process monitoring and diagnosis[J].Computers & Chemical Engineering,1998,22(12):S827-S830.

[3] Pettersson J,Gutman P O.Automatic tuning of the window size in the box car back slope data compression algorithm[J].Journal of Process Control,2004,14(4):431-439.

[4] Li X,Qiu H,Zhu Y.Research and design of lossy compression algorithm in embedded real-time database[C]∥Proc of the 2nd International Conference on Mechatronics and Automatic Control,2015:1027-1034.

[5] Mah R S H,Tamhane A C,Tung S H,et al.Process trending with piecewise linear smoothing[J].Computers & Chemical Engineering,1995,19(2):129-137.

[6] Bristol E H. Swing door trending：Adaptive trend recording[C]∥Proc of National Conference, 1990:749-753.

[7] Wang Ju, Fang Ding-yi, Chen Xiao-jiang,et al.Data compression of wireless sensor networks in the heritage monitor [J].Journal of Xidian University,2012,39(1):157-162.(in Chinese)

[8] Yu Song-tao,Wang Xiao-kun,Zhao Li-qiang,et al.The improved algorithm for SDT based on the dynamic adjustment of tolerance[J].Journal of Beijing University of Chemical Technology (Natural Science),2013,40(3):109-113.(in Chinese)

[9] Qu Yi-lin,Wang Wen-hai.Automatic parameter control SDT algorithm for process data compression[J].Computer Engineering,2010,36(22):40-42.(in Chinese)

[10] Zhang Jing-tao, Wang Hua,Wang Hong-an.Accessing and compressing of real-time data[J].Control and Instruments in Chemical Industry,2003,30(3):47-50.(in Chinese)

[11] Duan Pei-yong,Zhang Mei,Tang Tong-kui.A swing door trending(SDT) algorithm and its application to compressing process data received by local operation network nodes[J].Information and Control,2002,31(2):132-135.(in Chinese)

[12] Ning Hai-nan. A new process data compression algorithm based on SDT algorithm[J].Computer Technology and Development,2010,20(1):25-28.(in Chinese)

[13] Zhang Jian, Liu Guang-bin. A new data compression based on ISDT algorithm and its performance analysis[J].Fire Control and Command Control,2007,32(2):80-82.(in Chinese)

[14] Xing Rui,Qi Qi,Zheng Tao.Improved SDT algorithm [J].Computer Engineering and Design,2013,34(2):515-518.(in Chinese)

附中文参考文献：

[7] 王举,房鼎益,陈晓江,等.文物监测中无线传感器网络数据压缩算法[J].西安电子科技大学学报,2012,39(1):157-162.

[8] 于松涛,王晓琨,赵利强,等.基于容差动态调整的旋转门(SDT)改进算法[J].北京化工大学学报(自然科学版),2013,40(3):109-113.

[9] 曲奕霖,王文海.用于过程数据压缩的自控精度SDT算法[J].计算机工程,2010,36(22):40-42.

[10] 张景涛,王华,王宏安.实时数据的存取与压缩[J].化工自动化及仪表,2003,30(3):47-50.

[11] 段培永,张玫,汤同奎.SDT算法及其在局域控制网络中压缩过程数据的应用[J].信息与控制,2002,31(2):132-135.

[12] 宁海楠.一种基于SDT算法的新的过程数据压缩算法[J].计算机技术与发展,2010,20(1):25-28.

[13] 张健, 刘光斌. ISDT算法的数据压缩处理及其性能分析

[J].火力与指挥控制,2007,32(2):80-82.

[14] 邢锐,祁奇,郑滔.改进的SDT算法[J].计算机工程与设计,2013,34(2):515-518.