基于Poly IIR方法悬臂梁模态参数识别与研究

侯尧花， 张占一， 黄晋英， 马广轩， 沈 松

(1. 中北大学机械与动力工程学院，山西 太原 030051; 2. 北京东方振动和噪声技术研究所, 北京 100085)

0 引 言

悬臂梁结构已广泛应用到许多大型旋转机械的叶片模型中，其固有振动是旋转机械振动中最常见的振动形式之一[1-3]。在风机叶片高速旋转的过程中，由于受到各种交变载荷的长时间冲击，叶片自身会发生非常明显的受迫固有振动，并且在工程应用中受到酸性水、大气等外界条件腐蚀影响，对基于悬臂梁模型的叶片破坏极大，因此必须对旋转的叶片结构设计提出更高的要求[4]。

郭金泉等[5]利用平稳小波变换来识别悬臂梁上的缺陷；赵亮等[6]利用广义哈密尔顿原理及假设模态法得出悬臂梁系统动力学方程轴向运动，得到了材料属性指数越大、梁刚度越大、振动频率越大而振幅越小的结果；戴震等[7]研究了等截面悬臂梁自由落体冲击实验分析，得到了悬臂梁在冲击作用下的应力状态，没有对悬臂梁的冲击响应谱进行分析，因此对悬臂梁的力学传递特性的研究具有一定的局限性。张金轮等[8]利用插值矩阵法分析轴向受载的Euler-Bernoulli 梁双向弯曲与扭转耦合振动；苏军等[9]研究了一种悬臂梁式的发动机叶片扭转和弯曲变形同步测量的新方法；马辉等[10]进行了斜裂纹悬臂梁非线性振动特性分析，仅考虑了弯曲振动对裂纹的影响，得到随着裂纹角度的增加，裂纹导致的悬臂梁系统非线性特性更为明显，但是悬臂梁在扭转变形时对裂纹的影响更大，因此需要更进一步研究扭转变形对裂纹的研究。

以上学者集中于悬臂梁裂纹对模态参数的影响，没有对悬臂梁的扭转与弯曲变形进行详细的实验研究，但是挥舞弯曲与扭转变形对于叶片的结构安全影响较大，因此有必要进行悬臂梁的弯曲与扭转模态分析。在模态参数识别方法中，许多文献利用的方法包括ERA法、EFDD法、Poly MAX法[11-15]等，但是特征值算法拟合时必须先算脉冲响应函数，降低了计算效率，Poly MAX法的Hankel矩阵的系数需要复数运算，耗时较长而且对密集模态参数的识别具有一定的局限性，因此本文基于Poly IIR法对悬臂梁的弯曲与扭转变形进行模态测试，为叶片等悬臂梁结构系统的振动特性分析、振动故障诊断和预报以及结构动力特性的优化设计提供参考依据。

1 悬臂梁的模态理论分析

实际的振动系统都是弹性体，它的振动需要时间与空间坐标的函数来描述，其运动不再是二阶常微分方程组，而是通过偏微分方程来表示，本文拟利用Euler梁模型进行理论分析计算，它的主要特点为在同一XOY平面内梁的各阶模态振型做横向振动，主要变形为弯曲变形，在低频振动时可以忽略剪切变形以及截面绕中心轴转动惯量的影响。

通过材料力学的平衡面假设得知，弯矩与挠度的关系为然后代入力平衡方程中得到

当令p=m时，得到梁的横向振动为

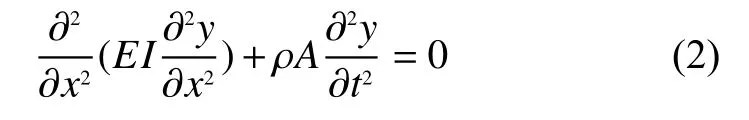
假设梁的主振动为y=Y(x)bsin(ωt+ϕ)，代入式（2）得到

根据材料力学理论得到等截面悬臂梁的边界条件为Y(0)=0,[EIY′′(X)]′=0,x=0,x=l。得到

悬臂梁各阶固有频率为

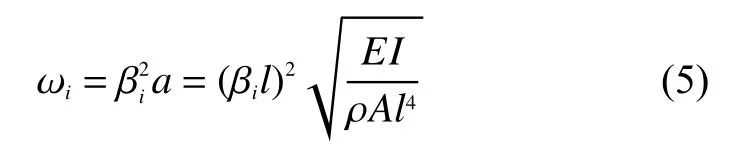
主振型为

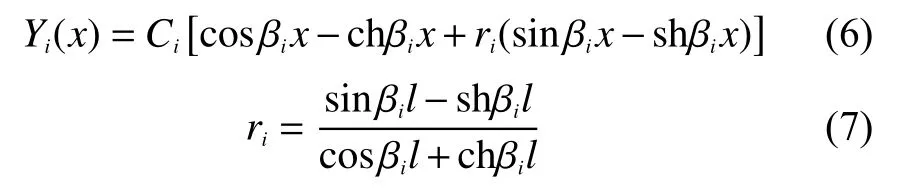
2 有限元分析计算

Workbench分析选用solid 186实体单元,悬臂梁的横截面为矩形截面，长度L=600 mm，宽度b为50 mm，厚度h为8 mm，弹性模量E为2×1011Pa，泊松比μ=0.3，密度ρ为7800 kg/m3。按照上述悬臂梁参数，利用Workbench对悬臂梁振动模态频率进行求解，得到前5阶弯曲频率分别为 10.247 ，64.192 ，179.75 ，352.23， 582.82 Hz。扭转频率分别为231.87 ，698.17 ，1172.1 Hz，限于篇幅只给出前3阶模态振型，如图1和图2 所示。

3 实验模态分析计算

3.1 Poly IIR 算法理论分析

Poly IIR模态识别方法利用IIR滤波原理推导出其频响函数特征方程系数，可以得到和模态频域参数识别Poly MAX法同样清晰的各阶模态稳定图，此算法理论严密，计算过程简单，如果 SISO系统的脉冲响应函数h(k)已知，其频响函数为

图1 悬臂梁前3阶弯曲模态有限元结果

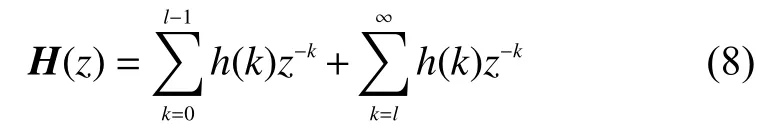
此处是采样间隔，是脉冲响应函数，是波形点数或长度，这是离散谱对应频率点在右端第2项为截断的部分对应的频谱，在所有频域法中，这项是未知的结果。

假定n阶模态的FRF写为

此处令N=2n，则有

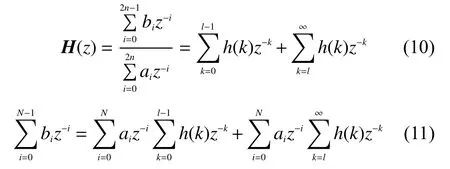
由于式（11）中只有多项式的分母为系统的频率特征方程, 取较低的L−N个方程构成：

图2 悬臂梁前3阶扭转模态有限元结果

对于MIMO系统来说，有q个响应点和p个激励点，式(3)中的系数矩阵ai具有维数p×p，而且a0=Ip×p，系数bi和脉冲响应函数序列h(k)可看作是的行矢量，对应同一响应点的p个激励点，因此得到：

特征方程系数矩阵为H矩阵所有元素的平方和取最小值。计算出(N+1)p维对称方阵并且矩阵M为

所有元素直接从时域数据得到，不需要额外的运算，更不需要复数的运算，比Poly MAX方法处理速度快了20%左右，模态参数识别率也提高了12%左右。特征方程为

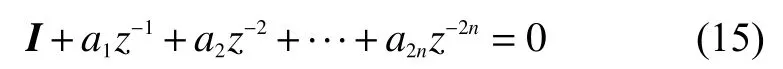
第r阶模态的频率和阻尼为

3.2 悬臂梁的模态实验

选取的悬臂梁尺寸为600 mm×50 mm×8 mm(长×宽×高)，材料为钢。实验过程首先把悬臂梁分10等分，总共22个测点，利用2个9824 ICP型加速度传感器分别布置于第10、13两个测点，这样放置到了最佳测试点，使该处的ADDOFA值最大，提高了信号的信噪比，因此本实验需采用MIMO实验法，提高模态特征方程的解耦性，识别同一频率附近不同的悬臂梁模态振型。

此次实验步骤如下：

1）在悬臂梁的左右两侧沿着变形最大的2个测点处分别布置2个9824型ICP加速度传感器，然后安装好MSC-1基于尼龙头的小力锤加力信号调理棒，利用双BNC线接入数据采集仪，详细布点位置，如图3所示。

2）进行基于锤击法的悬臂梁模态测试实验，首先进行预实验，得到合适的激励采样频率，然后利用DASP变时基技术得到较低的响应信号采样频率。

3）然后进行MIMO实验模态过程。

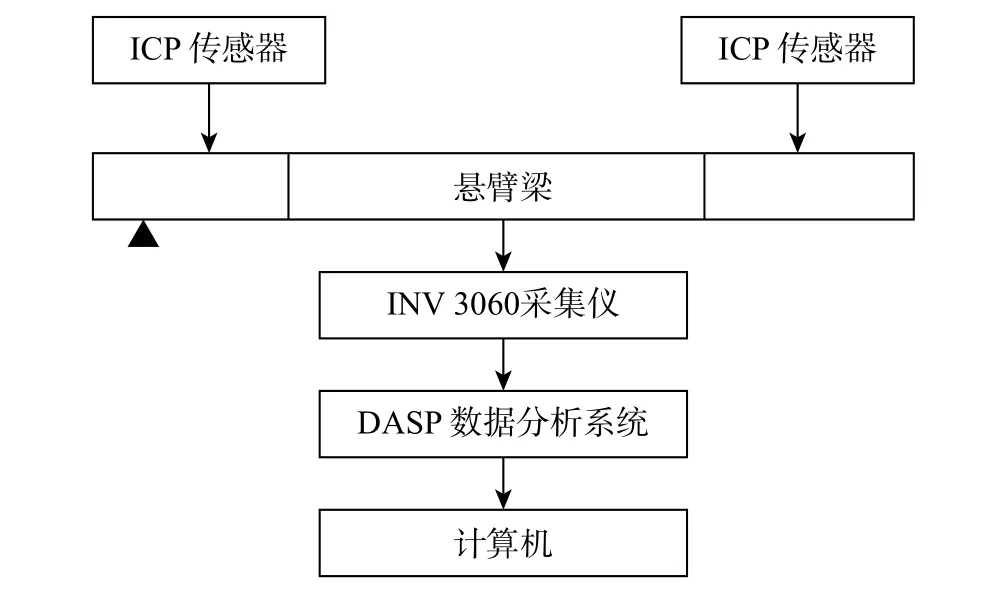
图3 悬臂梁模态实验现场连接图

4）利用基于Poly IIR方法进行模态参数识别。

5）得到悬臂梁实验模态固有频率与振型。

6）可以通过结果输出模态质量与模态刚度来验证实验结果的准确性。

由图4可以看出单个测点的频响特性函数的各阶频率信噪比非常好，说明本次实验数据的有效性，通过对所有测点的频响函数进行集总显示得到如图5所示，可以明显看出各阶密集模态结果。图6为利用Poly IIR得到的前5阶的弯曲模态振型，各阶固有频率分别为10.0 ，63.228，176.67，348.3，574.61 Hz，得到模态拟合结果解耦性好，峰值点突出，虚假模态几乎没有，说明该方法的准确性与稳定性指标非常好；图7为悬臂梁理论结果和实测频响曲线，得到实测值与理论值几乎重合；图8为振型相关矩阵校验检查模态分析结果，得到各阶振型的正交性良好。

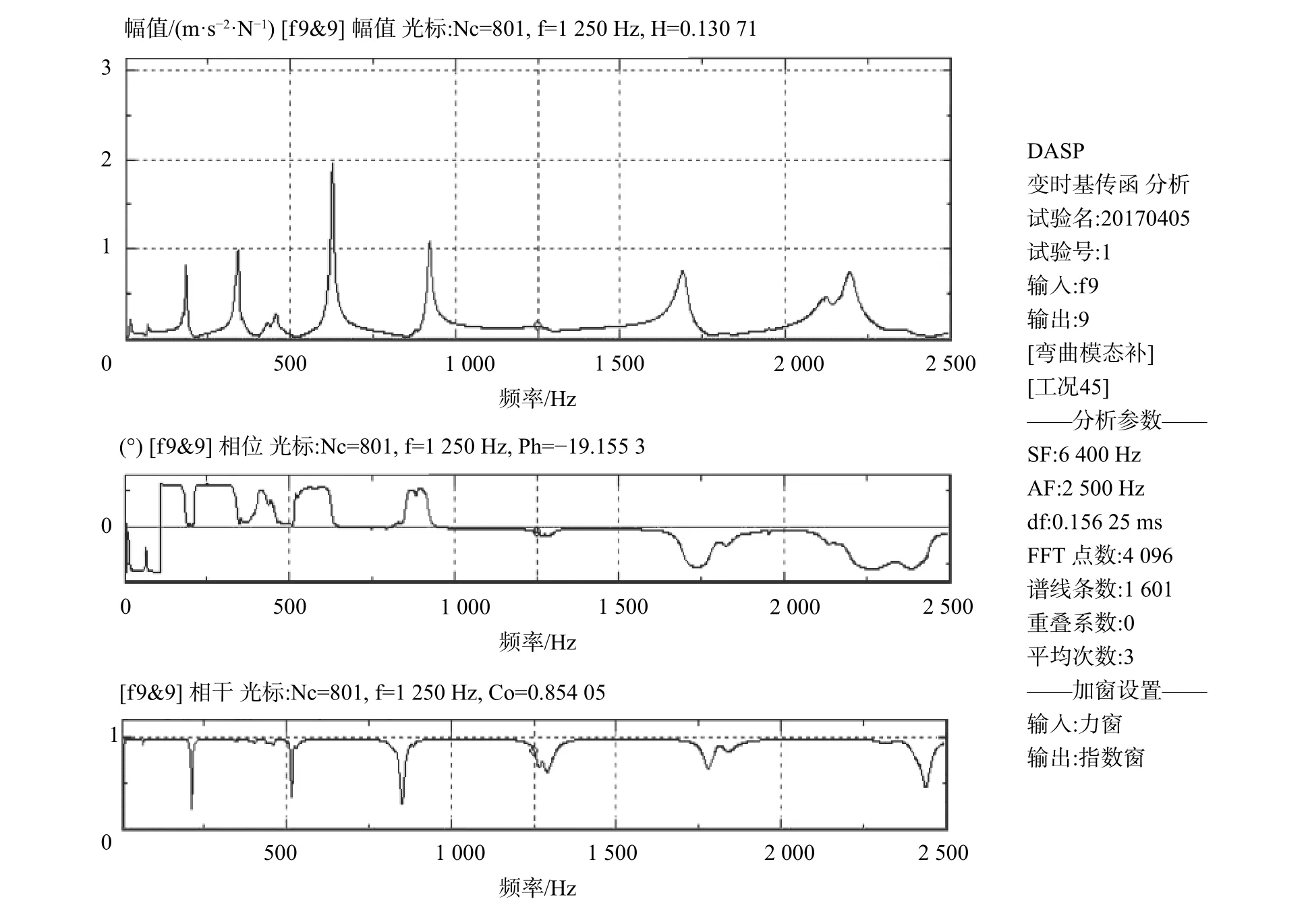
图4 单个测点的FRF与相干系数曲线

图5 所有测点的FRF函数线性组合曲线

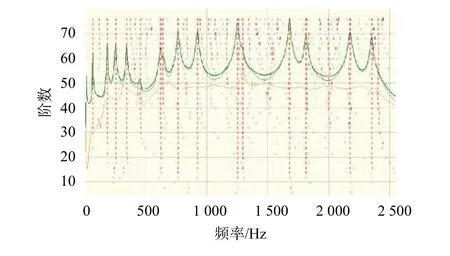
图6 Poly IIR模态拟合结果示意图

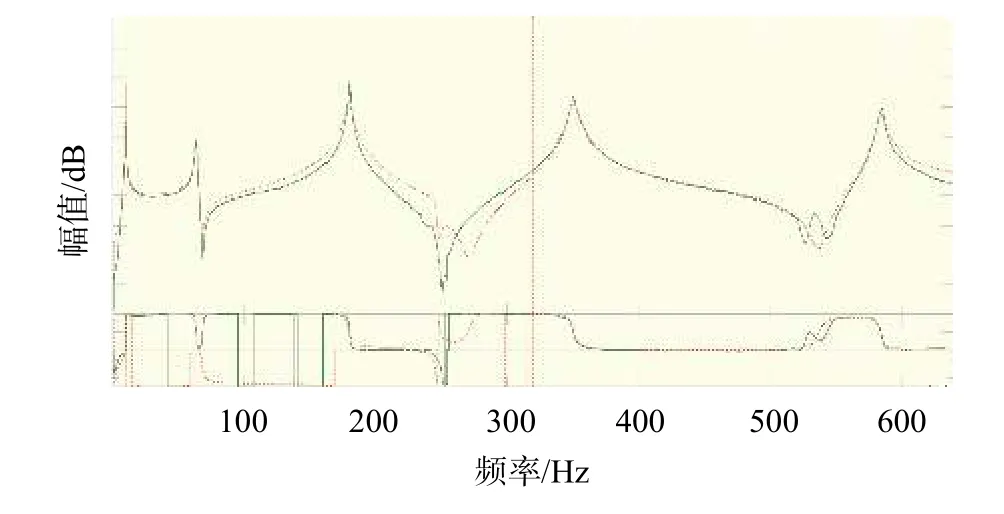
图7 理论计算与实测结果对数幅值对比曲线

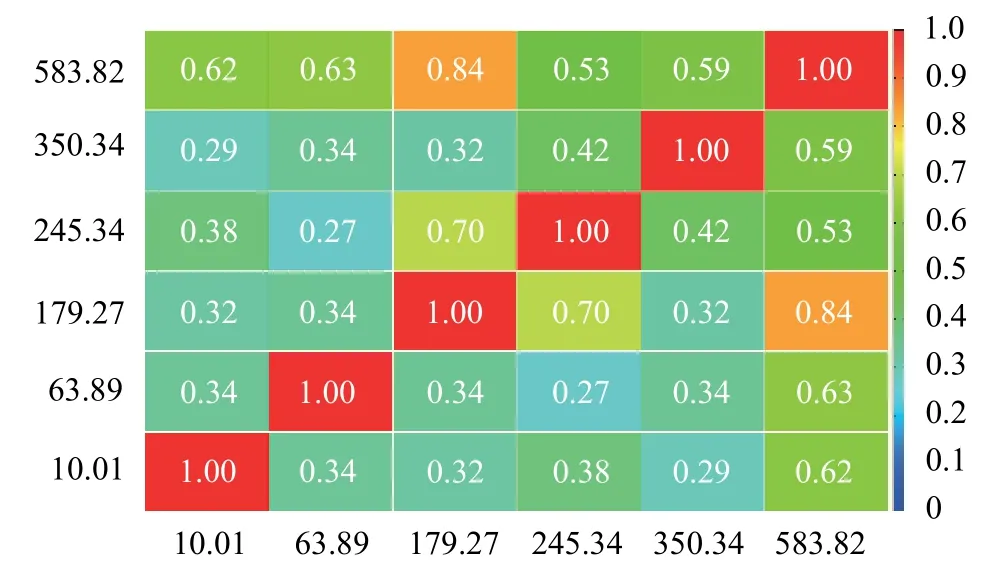
图8 模态相关性Cross MAC值计算结果

4 分析不同实验结果

通过前面的理论计算以及有限元分析得到悬臂梁的前5阶固有频率与振型，然后通过对悬臂梁进行实验模态分析得到悬臂梁的弯曲与扭转模态结果，如图9和图10所示。

图9 悬臂梁前5阶弯曲模态振型结果

图10 悬臂梁前5阶扭转模态振型

表1 弯曲实验与仿真结果比较

由表1中的实验结果可以得到悬臂梁的弯曲变形与扭转变形的模态振型具有相似之处，但是扭转变形对叶片等悬臂梁的结构共振损伤影响更大，在弯曲变形中，各阶固有频率基本满足βil的平方与1阶固有频率的乘积，而扭转变形的各阶固有频率为2i−1阶数与1阶频率的乘积，但是扭转1阶固有频率为241.87 Hz，对比有限元分析的1阶频率偏大，说明ICP传感器附加质量对悬臂梁扭转频率产生一定的影响，可为后续对不同附加质量对悬臂梁各阶模态频率的影响提供参考。

5 结束语

本文对悬臂梁进行了比较详细的理论仿真计算，建立了悬臂梁的振动力学模型，得出了悬臂梁各阶固有频率理论表达式，利用有限元分析了悬臂梁弯曲与扭转模态，然后利用Poly IIR方法拟合得到了悬臂梁的各阶弯曲模态与扭转模态实验结果。

悬臂梁的的各阶频率主峰非常明显，因此验证了Poly IIR方法对同一结构不同方向之间的模态频率拟合识别的优越性。通过对悬臂梁的弯曲与扭转模态分析，以及前期对简支梁的模态实验分析研究中可知，各阶固有频率与一阶频率成线性比例关系。

根据悬臂梁的各阶模态参数对比，可以为风机叶片的强度设计提供参考，包括增大叶片根部的强度设计，尽量避免风机转子的1阶临界转速频率靠近叶片1阶模态频率。

[1]赵荣珍, 芦颉, 苏利营. 风力机旋转叶片的刚柔耦合动力学响应特性分析[J]. 兰州理工大学学报, 2016, 42(6): 36–42.

[2]胡草笛, 王长路, 韦乐余,等. 叶轮参数对垂直轴风机风能利用系数的影响分析[J]. 机械强度, 2016, (02): 317–321.

[3]乔社宁, 李兵. 离心式风机含裂纹叶片的试验模态分析[J].流体机械, 2016, 44(11): 11–14.

[4]李春旺, 王澈, 李强, 等. 基于热固耦合预应力的发 动机叶片模态分析方法[J]. 空军工程大学学报（自然科学版）, 2016,17(2): 1–4.

[5]郭金泉, 陈垂福, 杨晓翔, 等. 辅助质量块—单裂纹悬臂梁耦合系统固有频率的理论研究及其应用[J]. 固体力学学报,2016, 03: 264–272.

[6]赵亮, 胡振东. 轴向运动功能梯度悬臂梁动力学分析[J]. 振动与冲击, 2016, 35(2): 124–128.

[7]戴震, 宋选民, 李志强, 等. 等截面悬臂梁自由落体冲击实验分析[J]. 实验室研究与探索, 2016, 35(1): 16–18.

[8]张金轮, 葛仁余, 韩有民, 等. 插值矩阵法分析轴向受载的Euler–Bernoulli 梁双向弯曲与扭转耦合振动[J]. 合肥工业大学学报（自然科学版）, 2017, 40(3): 373–378.

[9]苏军, 安中彦, 于云飞, 等. 发动机叶片扭转和弯曲变形同步测量新方法[J]. 实验力学, 2017, 32(2): 279–285.

[10]马辉, 曾劲, 郎自强, 等. 斜裂纹悬臂梁非线性振动特性分析[J].振动与冲击, 2016, 35(12): 86–91.

[11]KIM I W, RYU B J, KIM Y. Modal analysis and experiment of a simply–supported beam with non–uniform cross sections[J]. 2015, 16(12): 8654–8664.

[12]惠雷, 黄成, 荀勇. 采用EFDD法对系杆拱桥模态试验的分析[J]. 公路工程, 2015(6): 129–132.

[13]万成, 严波, 吕中宾, 等. 基于多通道模态分析的输电线路舞动特征识别[J]. 振动与冲击, 2016, 35(19): 132–137.

[14]张少波, 李美, 姜伟娟. 纯电动汽车减速器振动特性的模态分析[J]. 机械设计与制造, 2015(4): 224–227.

[15]李玉刚, 叶庆卫, 周宇, 等. 基于模态参数提取的随机子空间辨识算法改进[J]. 中国机械工程, 2017(1): 69–74.