Pascal函数矩阵的推广与应用
蔡杰锋
(闽南理工学院,福建 石狮 362700)
1 Pascal矩阵与Pascal函数矩阵的基本概念
Pascal三角形(又称杨辉三角形)最早是由中国南宋数学家杨辉发现的,用以描述二项式展开的系数,其形式是一个n层的三角形,第k层有k个正整数,分别对应二元多项式(a+b)k-1的展开式的k个项的系数,即:
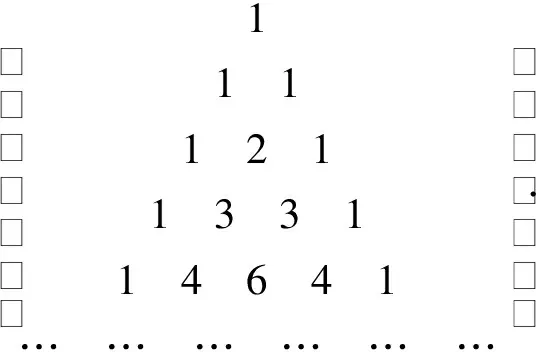
为了方便利用矩阵工具来研究Pascal矩阵,将其写成下三角的形式,就得出所谓的Pascal矩阵:

用严格的符号表示就是:
其中,Pn是n+1阶方阵,Pn(i,j)表示其(i,j)元.
Pascal矩阵Pn(i,j)有很奇妙的性质[1],其中,有两个性质较为重要:
(1)Pn是下三角的可逆矩阵;
(2)Pn的对角元都是1,所以特征值都是1.
Pascal函数矩阵是Pascal矩阵的推广,其引入了一个自变量,基本形式为:
其中,Pn[x]是以x为自变量的n+1阶函数矩阵,Pn[x](i,j)表示Pn[x]的(i,j)元.
显然,当x=1时,Pn[x]就是Pn.
关于Pascal函数矩阵的性质详见文献[1~3],其中,有两条性质较为重要:
(1)Pn[x+y]=Pn[x]·Pn[y](x,y∈R);
(2)Pn[x]-1=Pn[-x](x∈R).
2 Pascal函数矩阵的推广
为了方便起见,先约定以下矩阵运算的符号:
对m×n阶矩阵A,A(i,j),A(i,:),A(:,j)分别表示矩阵A的(i,j)元,第i行,第j列,其中1≤i≤m,1≤j≤n.
至今,Pascal已有多种类型的推广形式,具体可参见文献[4~6].
纵观其多种推广形式,不外乎是将未知函数项xi-j推广为其它类型的函数.因此,可以用任意类型的函数代替xi-j,得到新的推广形式.但是这样得出的函数矩阵的范围就太大了,研究价值不大.因此我们要找到Pascal函数矩阵的某些绝妙的性质,然后试图在不改变这些性质的情况下对其进行推广,这样得出的推广形式才会有研究价值.
纵观其多种已有的推广形式,都保持Pascal函数矩阵的一条绝妙的性质:
定理1Pn[x+y]=Pn[x]·Pn[y](x,y∈R).
证明上式等价于:
Pn[x+y](i,j)=Pn[x](i,:)·Pn[y](:,j),
对1≤i Pn[x](i,:)·Pn[y](:,j)=0=Pn[x+y](i,j). 对1≤j≤i≤n+1, 证毕. 现在再考虑一下如何推广Pascal函数矩阵的定义,使得推广后仍然保持与定理1类似的性质. 首先,先将Pn[x]定义中的某些概念一般化:Pn[x]的定义中,所需的未知因子是xk(0≤k≤n),可以将未知数x的取值空间换为一个半群(M,*),并且将幂次方函数换作M上的可列个实算子:Δk(k=0,1,2,...),类似地给出广义的Pascal函数矩阵的定义: 如上定义的广义Pascal函数矩阵不一定有跟定理1类似的性质.因此,就需要找出满足类似性质的某些充分条件.而在这之前,先要考虑一下怎样阐述定理1的推广形式: Pn[x+y]=Pn[x]·Pn[y](x,y∈R). 这个式子的右边是矩阵乘法,不需改变,左边式子中x+y的加法运算可以推广为半群(M,*)上的二元运算*,所以定理1的推广形式应该是: (1) 寻找使式(1)成立的充分条件,模仿定理1的证明: 式(1)等价于: (2) (f*g). 因此,可以得出式(1)成立的一个充分必要条件: 结合以上的论述,就得出一种较为广泛的有研究价值的Pascal函数矩阵的推广: 定义1给定一个半群(M,*),再给定满足以下条件的实算子{Δk|k=0,1,...}: 对每个f∈M及正整数n,定义一个n+1阶的函数矩阵 称其为半群(M,*)上的广义Pascal矩阵. 显然,由定理2,直接有: 利用抽象代数的理论,可以得出: 本节将上节推广的广义Pascal函数矩阵特殊化,构造几种特殊的推广形式,并给出其应用实例. 例1当半群(M,*)为实数加法群(R,+),实算子Δk是k阶幂算子xk时,所定义的广义Pascal函数矩阵就是一般的Pascal函数矩阵Pn[x].因此,上节定义的广义Pascal函数矩阵的确是一般Pascal函数矩阵的推广.此时,推论1就变成了定理1.又由于Pn[0]=In+1,根据推论2,有以下结论: 推论3Pn[-x]=(Pn[x])-1. 例如, 例2当半群(M,*)为n元实函数加法群,实算子Δk是k阶幂算子xk时,所定义的广义Pascal函数矩阵就是一般的Pascal函数矩阵的简单推广:Pn[f(X)],同样也有:Pn[0]=In+1(注意:这里的0表示零函数,而不是数字零),根据推论2,有: 推论4Pn[-f(X)]=(Pn[f(X)])-1. 例如, 例3当半群(M,*)为一元光滑实函数乘法半群(C(R),*),实算子Δk表示k次求导算子时,根据求导公式:下列式子成立: 从而,就可以定义特殊的广义Pascal函数矩阵: 又注意到半群(C(R),*)的单位元是恒等于1的函数f0(x)≡1,且再根据推论2,有: 根据上式,有以下关于数列的二项式反演关系: 推论6{an}和{bn}为两个实数列,则下列两种递推关系等价: 就等价于 再令上式的未知数x等于0,以及未知变量X,Y分别为(a1,...,an)T,(b1,...,bn)T,那么就可以得出以上两种递推关系等价的结论. 本文通过分析多种推广Pascal函数矩阵的形式和性质,得出了推广过程中始终保持的一个绝妙的性质(定理1);然后,在一个较为广泛的框架下给出了保持这个性质的充要条件(定理2);紧接着,根据这个充要条件给出了一种较为广泛的保持绝妙性质的广义Pascal函数矩阵;并且在最后给出了几种基于这种广义形式的特殊形式和应用. 本文所推广的广义Pascal函数矩阵是具有广泛研究价值的,对其进行更深入研究深有裨益. [1] CallG S,Velleman D J.Pascal’s matrices[J].Amer Math Monthly,1993,100:372-376. [2] Brawer R,Pirovno M.The linear algebra of the Pascal matrix[J].Linear Algebra Appl,1992,174:13-23. [3] Zhang Z Z.The linear algebra of the generalized Pascal matrix[J].Linear Algebra Appl,1997,250:51-60. [4] M Bayat,H Teimoori.Pascal k-eliminated functional matrix and Eulerian numbers[J].Discrete Appl Math,2001,49:183-194. [5] Z Zhizheng,M Liu.An extension of the generalized Pascal matrix and its algebraic properties[J].Linear Algebra Appl,1998,271:169-177. [6] 赵熙强,李琳.函数矩阵的进一步推广及应用[J].中国海洋大学学报,2015(3):136-140.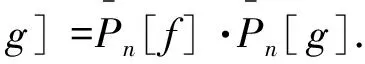




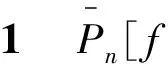


3 推广的Pascal函数矩阵的应用

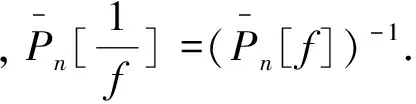


4 结论

