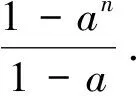例谈高中生数学解题的心理性错误
曹 瑜,张玉娟*,吕 谦
(1.鞍山师范学院 数学与信息科学学院,辽宁 鞍山114007;2.鞍山市第三中学,辽宁 鞍山 114012)
在中学生的数学学习中,解题与对习题的反思是其中非常重要的一个环节.学生通过解题,巩固所习得的数学知识,训练自身的数学思维能力;通过对习题进行反思整理,学生可以对解题的思路进行重新整合,不断锻炼解题能力,提升数学水平.因此,在教师教学的过程中,往往重点强调解题后的整理与反思.对于常见的错误,有经验的教师会在课堂教学中有针对性地进行讲解与分析,以避免学生再次出现该类错误.而对学生解题时还会出现错误,有的教师将其简单归咎于粗心大意或者知识点掌握不足.这导致教师在讲解习题时,直接重复正确答案,忽略学生真正的出错点;学生在听课时不能找到自己出现错误的本质原因,从而在一节习题课后依旧对问题存疑,无法正确地进行解题,使这种错误不断出现.教师认为自己讲清楚了,但学生依旧什么也没有听懂,不能起到习题课的真正作用.造成这种现象的真正原因是教师不能充分地重视学生出错的原因,成功解题除了依赖于智力品质和充足的知识储备外,学生本身的心理因素往往起到更大的作用.在同样的课堂教学中,基础水平相当的学生在解题上也会出现较大的差异,此时错误的出现与心理因素密切相关.因此,教师分析学生解题的心理性错误[1~5],对于提高教学效率、改进教学策略有重要意义.
1 心理能力不足
心理能力即人们从事心理活动所需要的能力.高中生解题过程中常因心理能力的限制导致在识别题目、对习题的信息加工及短期的工作记忆等方面出现错误.识别能力是指学生接触到题目之后,将问题模式与大脑中已有的知识经验建立联系,找出求解的方法.高中生常常对面对的问题感到茫然无措,百无头绪,这就是识别能力不足,无法将问题与知识结构进行对接.识别方面常见的典型错误为学生对已做过多次的习题无法再次识别辨认,对于解题过程中用到的公式感到陌生等.
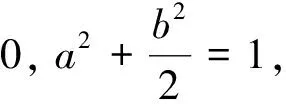
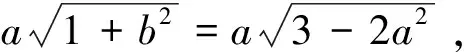
分析学生采用换元的方法尝试,但所得结果无法进行进一步的处理.这是属于识别能力缺乏的错误.
正解b2=2-2a2,则



即

解题过程中的记忆能力的不足主要是工作记忆能力不足.在此过程中,学生不断接收处理数据,这对他们暂时贮存信息的能力提出了一定的要求.解复杂的分类讨论问题时经常出现此种情况,解题后期忘记之前的分类,或是忘记求交集还是并集.
例2不等式x2-2ax+a+2≥0在x∈[1,3]时恒成立,求a的取值范围.
错解设f(x)=x2-2ax+a+2,函数的开口向上,对称轴为x=a,对此进行分类讨论:
若a≤1,则
f(1)=1-2a+a+2≥0,
解得a≤3;
若1 f(a)=a2-2a2+a+2≥0, 解得-1≤a≤2; 若a≥3,则 f(3)=9-6a+a+2≥0, 分析学生在计算过程中将参数的取值分为3个部分,a≤1,1 正解设f(x)=x2-2ax+a+2,则函数的开口向上,对称轴为x=a,对此进行分类讨论. 若a≤1,对称轴在定义域的左边,x>a时,函数f(x)单调递增,只需f(1)=1-2a+a+2≥0则f(x)≥0在x∈[1,3]时恒成立,解得a≤3,与大分类求交集,得a≤1; 若1 f(a)=a2-2a2+a+2≥0, 解得-1≤a≤2,求交集得1 若a≥3,对称轴在定义域右侧,x f(3)=9-6a+a+2≥0 因此,可以得到参数的范围a∈(-,2]. 学生在学习过程中,原有的知识结构具备固定的顺序,这种顺序影响了学生对新知识的编码,形成顺序心理.常见的顺序心理所导致的错误为: 例3已知ΔABC中,A∶B∶C=1∶2∶3,求sinA∶sinB∶sinC. 错解根据题目所给的A∶B∶C=1∶2∶3,直接得出sinA∶sinB∶sinC=1∶2∶3. 停留性错误建立在学生解相关类型题的经验上,是一种对于经验的呆板套用. 例4等差数列{an}的通项公式为an=2n-8,n∈N+.n为何值时,该数列的前n项和最小? 分析在求解等差数列的前n项和最值时,由于以往求二次函数最值只能得到一个解,学生不能及时地进行调整导致错误.这是学生停留在二次函数的经验中所产生的错误,属于停留性错误. 停留性错误很多情况下被认为与顺序心理相同,但二者有很大的区别.顺序心理更多的是题目本身的形式导致学生片面沿用所学,是客观条件给出的错误判断;而停留性错误则是学生过往经验的停留,是主观经验的直接影响. 在数学习题中,题目给出了各种各样的条件以供学生取用,此时学生倾向于发现简单直接的表面条件,而对于隐含在题目背后的条件则无法全面地找出来.在进行解不等式的教学中,教师经常会发现学生忽略分母不为0,而在解分式不等式时扩大了解集,将导致分母为0的解纳入解集范围.这种心理势态更多地被教师认为是马虎,将其归咎为单纯的学生个人问题,从而忽视了学生对基础知识掌握不足的问题. 错解原式化为x(x+2)(3-x)≥0,根据“穿根法”得到解集为x∈[-2,0]∪[3,+). 分析错解出现的原因有:一是忽略了“穿根法”的应用条件:自变量的系数为正值;二是忽略了分母不为0这一隐含条件. 正解原式化为 x(x+2)(3-x)≥0 (x≠3) 后,整理为 x(x+2)(x-3)≤0 (x≠3), 根据“穿根法”得到解集为 x∈(-,-2]∪[0,3). 错解利用均值不等式 因此 的最小值为4. 分析忽略均值不等式等号成立的条件,直接重复套用. 正解首先对原始式子进行展开变形,为 然后再套用均值不等式 相较于对隐含条件的忽视,学生更多出现的一种情况则是增加补充新的条件,这种心理现象称之为潜在假设——题目中并未给出条件,且并没有相关的隐含推导,学生依据过往经验和习惯性认知添加条件,导致解题错误.这种错误的产生原因有:一是学生对于基础知识掌握过于死板僵化;二是学生对题目重视不足,将其视为简单的巩固性练习. 分析学生直接认为ΔABC是锐角三角形.这是潜在假设错误. 分析潜在假设认为题中所给的f(n)是一个数列前n项和,但实际上它是通项公式. 正解分别列出f(n+1)与f(n) 因此 例10不等式x2+ax+1≥0在x∈R时恒成立,求a的取值范围. 分析运用参变分离的思想求解,潜意识认为x是一个正数.这是学生的潜在假设. 适当的解题焦虑有助于促进学生的解题亢奋情绪,而过度的焦虑则适得其反.学生在长期解题错误的过程中形成的紧张、逃避的心理态度,反映在习题上主要表现为试卷上解答题、应用题的大量留空,疲于思考,只接受直接答案,拒绝写出详细的解题步骤;有的学生将解题及整理视为形式化的重复,机械性地依照教师指示完成练习;有的学生则走向另一个极端,他们认为日常的解题训练并没有什么作用,从而轻视作业、练习,认为考试时解题正确即可,结果往往不如人意. 面对这样的情况,教师应当提起重视,首先从学生本身的情绪入手,在教学中运用数学游戏、数学史等材料,耐心培养他们的解题兴趣,形成正确的解题观念.在解题教学过程中,教师应摆脱无意义的重复行为,将教学重点转移至解题方法的深入阐述,包括其应用条件、适合的习题模式等,使学生真正理解练习的意义. 在解题错误的产生过程中,各心理因素并非独立作用.学生的解题过程中心理性错误是逐步产生的,每一步所蕴含的心理因素各不相同,最终导致的错解也是各因素综合作用影响的结果. 例11计算1+a+a2+…+an. 分析学生首先认为题目所给的等比数列可以直接应用公式,这是忽略a可能为1这一隐含条件所导致的错误.在计算过程中又由于题目所给的形式,认为这是n项之和,这是相关类型题的经验所导致的停留性错误. 综上所述,在解题过程中,学生的心理因素变化多样,多重因素综合导致了解题的失误.在教师进行教学时,不能简单认为解题的教学仅发生于习题课上,将纠正错误作为目标,重复正确答案.而应对题目和学生的错误进行针对性的分析,从学生的基础知识开始,强调基础概念和公式的掌握,活跃学生的解题思想,打破思维惯性;同时培养学生严谨审题的习惯,在解题过程中做到每一步骤有理有据,清晰明确,如此才能在心理层面逐步纠正学生的不良习惯. [1] 黄彩祥.高中数学解题心理性错误分析[J].数学教学通讯,2003,35(12):12-14. [2] 马文杰.高一函数教学中学生数学解题错误的实证研究[D].上海:华东师范大学,2014. [3] 刘向征.高中生数学解题心理性错误性别差异研究[D].西安:陕西师范大学,2010. [4] 波利亚.怎样解题[M].上海:上海科技教育出版社,2011. [5] 罗增儒.数学解题学引论[M].西安:陕西师范大学出版社,2001.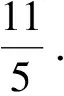
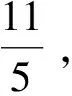
2 错误的心理势态
2.1 顺序心理导致的错误
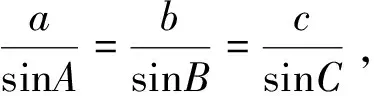

2.2 停留性错误
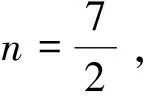
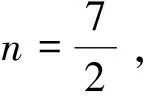
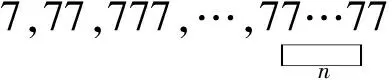

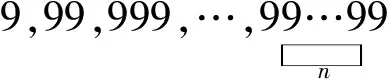
2.3 忽视隐含条件

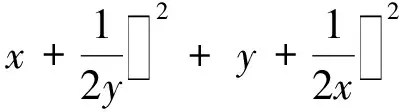

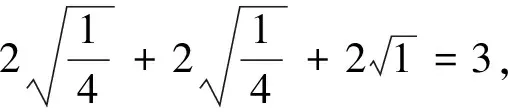
2.4 潜在假设
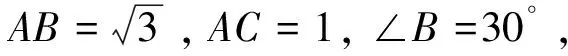
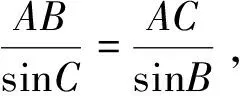
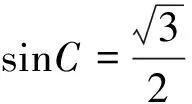
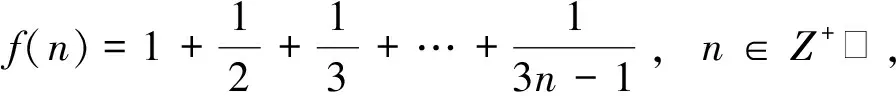
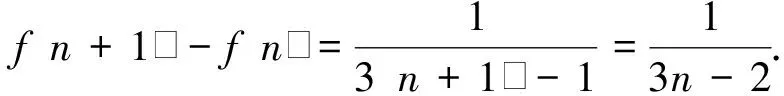
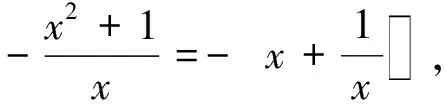
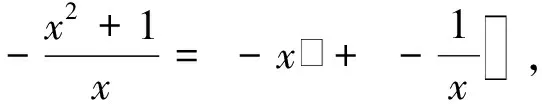
3 其他心理情况
4 总结