基于本征正交分解的缸内流场仿真校核方法探究

顾鹏，葛鹏辉，许敏

(上海交通大学汽车工程研究院，上海 200240)

活塞点燃直喷式(Spark Ignition Direct Injection)汽油机相比进气道喷射汽油机在燃油经济性和颗粒物排放方面具有很大的优势，并得到了广泛的研究和应用[1-2]。研究表明，缸内流场对发动机燃油雾化、火焰传播路径和速率具有重要的影响[3]，而缸内流场结构又受到诸多因素如进气道形状、进气歧管倾角和缸盖结构等的影响[4]。如果能够开发出较为准确的发动机三维模型，这将极大地节约发动机开发成本。因此，发动机的三维模型校核也显得尤为重要。

与传统的RANS仿真不同的是，大涡模拟和试验的结果都存在着强烈的循环差异，对发动机的三维模型校核带来了极大的障碍。而本征正交分解(Proper orthogonal decomposition)通过基函数(mode)为大涡模拟和试验结果提供了一个比较的基础[5]。Lumley 等[6]最早将本征正交分解的方法引入到湍流场的分析中，将湍流场中能量较大的大尺度涡团结构分离提取出来。由于发动机缸内流场同样具有高度湍流特性，因此该方法逐渐被用于发动机的流场分析中。Sirovich[7]提出的“snapshot”的本征正交分解方法，在与原先的直接法等效的情况下，大大提升了计算效率，也广泛应用于流场分析。在发动机流场试验和仿真分析方面，很多研究者都基于不同的试验和仿真工况做了很多有益的工作。秦文瑾、许敏等[8]证明了本征正交分解可以作为分析发动机缸内流场模拟结果准确性的有效工具。Fogleman等[9]通过相位固定的本征正交分解的方法，对不同曲轴转角的缸内流场变化进行了分析。陈豪等[10]指出目前对实际发动机流场结果本征正交分解的研究相对匮乏，并阐述了试验与仿真缸内流场比较的应用思路。此外，一些研究者对试验数据的完善，对缸内流场仿真校核的工作也具有重要意义。Druault等[11]通过本征正交分解对PIV的流场结果进行时间跨度上的插值，Borée 等[12]通过本征正交分解的方法阐述了时间和空间位置上的关联。

本研究在前人工作的基础上，着眼于基于本征正交分解的缸内流场仿真校核方法，从能量和模态的角度，全面合理地评价试验和仿真缸内流场结果的差异性，借此提出并建立缸内流场仿真校核的流程策略。

1 数值模型描述

1.1 发动机仿真方法

关于缸内流场循环的分析，大量基础性的研究是基于雷诺分解，建立对湍流脉动量的分析。雷诺方程的核心价值在于，将对湍流的研究转化为了建立可以求解的、与雷诺应力这个变量相关的输运方程。1887年提出的Boussinesq假设，通过与分子运动动量传递的类比，将雷诺应力转化为涡黏性系数，而涡黏性系数进一步地被分解为对湍流涡团的长度和速度尺度这两个变量的求解。在后续的缸内流场研究中区分零方程模型、单方程模型、多方程模型等，一定意义上就是在于求解这两个变量的微分方程的个数。Boussinesq假设之后，混合长度理论卡门相似理论等将涡团的长度和速度尺度以经验或者代数的方法表达，在早期的缸内流场分析中起到了很大的推动作用，但是它在时间、空间变化上的表征仍存在许多不足。因此，从1942年Kolmogorov和1945年Prandtl的研究开始，人们逐渐开始建立κ方程、涡黏度方程(Spalart-Allmaras)等单方程模型。现在主流的CFD软件中，频繁使用κ-ε,κ-ω等双方程模型，对于这些模型，研究者们还在不断地根据具体的使用情况进行修正，例如应用较广的压缩性修正、强旋流修正等。此外，在强调各向异性的缸内流场分析中，对雷诺应力直接进行分析的RSM模型也应用极广。

近几十年来，研究者们逐渐认识到缸内流场可以分解为一系列的有序流场结构，现在商业应用极广的LES(大涡模拟)实际上就是基于空间尺度的划分，将对应于不同尺度的涡团划分为可解尺度和亚网格尺度，两者分别使用直接求解的方法和假设模型的方法进行分析。大涡模拟的核心前提是大尺度涡团与仿真时设置的初始和边界条件相关性较大，而小尺度涡团受它们的影响较小，大尺度涡团的各向异性和小尺度涡团的各向同性促成了大涡模拟将它们分开处理的合理性。

大涡模拟的思路如下：首先消除小涡的脉动影响，得出局部的平均场，即为大尺度场，而亚网格尺度场则为原始流场与该平均场的差值。大尺度场根据网格，由N-S方程直接求解，而对于亚网格尺度场，常用的模型有Smagorinsky模型、WALE模型、亚网格单方程模型以及动态结构模型。其中，对于Smagorinsky模型和亚网格单方程模型，在后续LES的研究和计算中模型系数进行了修正，以满足更多的情况，进而产生了动态Smagorinsky模型[13]和亚网格单方程模型。

不管是直接数值模拟(DNS)，还是雷诺平均(RANS)或者大涡模拟(LES)，都因为其假定或者切入角度的问题，各自存在计算精度、计算能力、结果呈现等方面的问题，在实际的情况中研究者或者商业工程师应根据具体情况适当选用。而大涡模拟对于大尺度涡团脉动的保留，相对合理的计算能力要求以及对循环变动的分辨，使得它在未来的发动机仿真中将有极大的发展空间。本研究采用的仿真方法即为大涡模拟法。

本研究中大涡模拟的发动机是G4VDI GM 的四冲程直喷发动机，转速1 300 r/min下，涡流控制阀完全开启，形成一个低涡流比的工况，使得缸内流场湍流强度更强，这对于仿真模型校核更有意义。与试验相匹配的发动机结构见图1。基本网格大小为4 mm，在下止点处设置了109万个网格。针对仿真具体位置和情况，对网格进行优化。在阀附近最小网格为0.25 mm，图2示出网格优化的一些细节位置和内容。

图1 发动机结构

图2 网格优化设置

仿真所有的数据来源与试验严格对应。试验采用二维粒子图像测速方法来获得同样工况下的流场数据，在1台排量0.55 L、四冲程、4气门单缸光学发动机上进行(见图3),发动机具体运行参数见表1。

图3 光学发动机台架

缸径/mm86进气温度/℃25活塞行程/mm94.6转速/r·min-11 300连杆长度/mm160进气门开启时刻(ATDC)/(°)-366压缩比11∶1进气门关闭时刻(ATDC)/(°)-114进气涡流比0.55排气门开启时刻(ATDC)/(°)131进气压力/kPa40排气门关闭时刻(ATDC)/(°)372

1.2 本征正交分解方法

POD(本征正交分解)对于湍流的研究不同于传统的统计方法，不仅提供了周期平均流场和脉动流场宏观的分析，而且提供了更多内燃机循环变动的细节。POD在流场循环变动的分析中，将多循环同一时刻的流场提取为一系列基函数，而基函数对应的流场结构可以重新组合为原始循环的流场。鉴于是基于特征值的提取，POD的前几个基函数已经包含了大多数的流场动能，即通过分析前几个POD 模态，可以得到对于缸内流场循环变动的很多细节信息。

POD在很多领域都有着关键的应用，也存在许多的推导方法。本研究将结合PCA(主成分分析)的思路，理解POD计算过程在缸内流场分析中的真实含义，分析POD在缸内流场分析中的原理。

图4左侧为发动机缸内流场的速度矢量图，右侧为类比建立的一个n×n的样本，共有n2个节点。每一个节点包含对应矢量ui,j的信息。假定uk是第k个循环的速度场，其包含了该样本所有节点的矢量信息。

图4 速度场矢量示意

(1)

定义总体u为循环速度场uk的集合，行数为N，N即为样本总数，每个样本的维度为n2。

u=u1,u2,…uNT。

(2)

PCA的核心思想是去除冗余的维度和降噪，这两点与缸内流场分析中POD的思路不谋而合。对于总体u的分析，首先计算u1,u2,…uN的期望E(u),然后计算离散的协方差矩阵C。

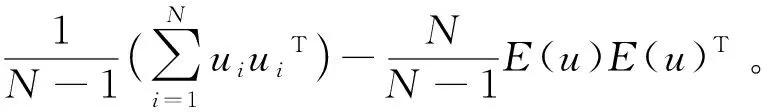
(3)

为了分析方便，在计算协方差矩阵之前，一般会进行数据中心化处理，即令E(u)=0，则有：

(4)

以三维的协方差矩阵为例可以发现，协方差矩阵的对角线实际上体现了各自维度的方差，非对角线元素体现了维度间的相互影响。PCA的思想是去除冗余的维度和降噪，实际上一方面尽可能使保留的维度之间相关性小，另一方面使保留的维度方差较大。从信号与数学意义上分析，根据最大方差理论，方差的大小体现的是包含能量的大小。

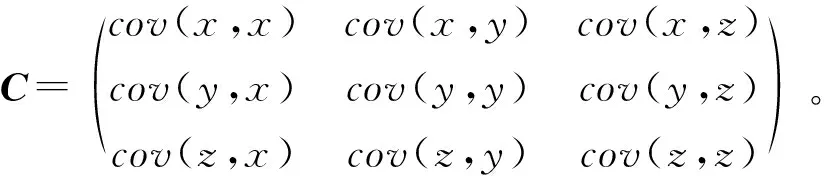
(5)

因此，对该矩阵C进行对角化处理并求特征值。对应于C的最大特征值的特征向量，就是POD的主要模态。也正因如此，POD的主要模态对应于大的方差，包含了大多数的能量，并且POD的降维过程也去除了不必要的维度。本研究从PCA的思路推导出这一点，也阐释了POD的处理过程对于缸内流场分析的实际含义。

2 缸内流场校核方法论

2.1 基于能量的缸内流场校核

将试验的50个循环(B1～B50)和仿真的50个循环在不破坏次序的情况下组成一个新的流场矩阵，对其进行本征正交分解。因此，试验和仿真得到共同的模态(100个)。虽然在物理意义上无法区分试验和仿真的模态，但正是由于试验和仿真有相同的模态，才使得模态前面的能量系数足以代表某个模态下试验和仿真的能量大小。

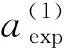
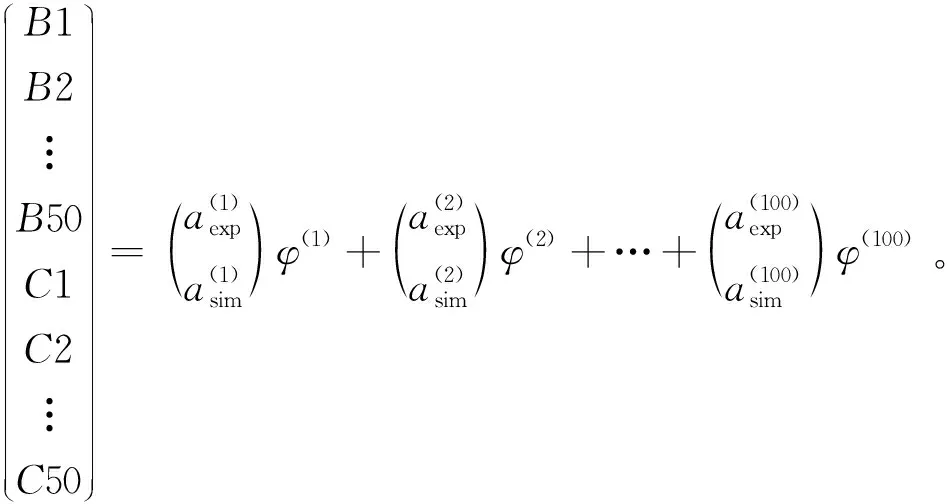
(6)

(7)

COV(变异系数)在考虑平均值的基础上体现了系数的离散程度，发动机研究中常用它来分析多循环间的变动性，比如平均有效指示压力变异系数。

(8)

这种基于能量的校核方法在一些仿真分析中已经开始广泛使用，并对于试验和仿真的分析工作提供了很多有力的支持。陈豪等[10]利用本征正交分解的方法分析了缸内进气和压缩过程中的循环变动以及气流的发展变化，并提及了试验与仿真缸内流场比较的应用想法。K. Liu等[14]利用本征正交分解的方法着重分析了大涡模拟的结果，并借此讨论了流场的循环差异。但该方法只考虑了主导模态的能量校核，并没有全面地对仿真模型进行校核，因此需要增加对仿真和试验各自的主导模态的校核。

2.2 基于模态相关性系数的缸内流场校核

在发动机缸内流场试验和仿真结果的对比中，面对的难题是缺乏一个行之有效、单一的方法来进行衡量。若是从能量的角度来分析和比较主要模态前面的系数，缺陷在于试验和仿真结果的差异是模态系数的差异和模态本身的共同作用。当某些循环中存在能量较大的流场结构时，该结构会严重影响模态，进而使得模态系数偏向试验或者仿真，不能更好地校核仿真数据。如果能够增加对模态的分析和比较，将大大提高模型校核的准确性。因此，对模态之间的相关系数进行分析，能够极好地解决上述问题。具体思路是将试验和仿真结果的差异转化为两个系数之间的比较，而这两个系数是在考虑了所有主要模态的基础上得到的。这种基于模态特征方法的比较流程见图5。

一般而言，选择前5个模态来进行对比，因为从能量上讲，前5个模态包含了流场的大多数能量和涡团结构。在实际应用中，可以根据工况和计算结果进行调整。图6示出了前1～5个模态能量系数的和，可以发现，前5个模态包含的能量非常接近于1，均在0.998以上。因此，本方法选取前5个模态来表征缸内流场是合理的。将试验和仿真的所有循环进行混合POD分析，并将其结果作为衡量仿真和试验结果的基准。与此同时，将试验的50个循环和仿真的50个循环分别进行POD分析，计算它们与混合POD主要模态之间的相关性系数后进行比较，从而得出试验和仿真结果的差异。

图5 基于模态相关性系数的校核流程

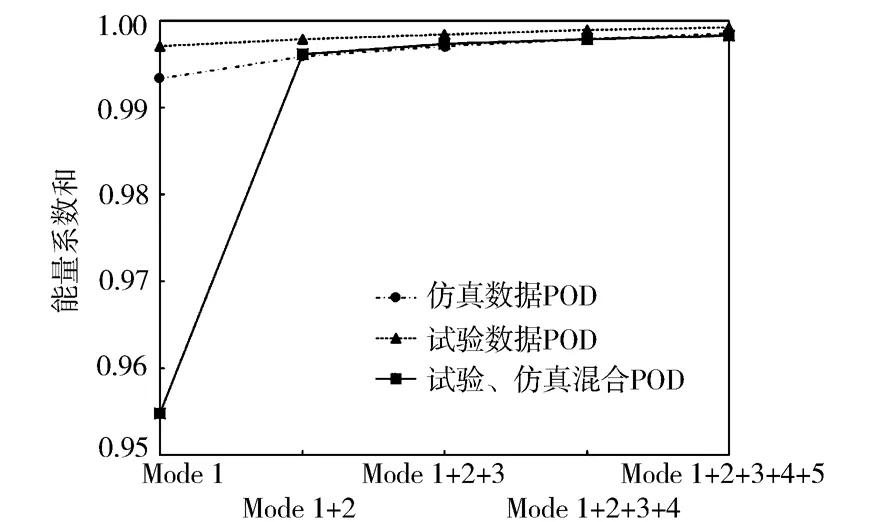
图6 本征正交分解主要模态包含的能量之和

对于模态之间相关性分析，使用以下几种相关系数：

SI(Structure index):

(9)

MI(Magnitude index):

(10)

KER(Kinetic energy ratio):

(11)

MI*(Magnitude index*):

(12)

式中：u，v分别为试验和仿真的主要模态的速度场矩阵。

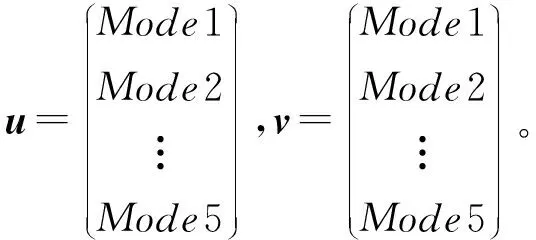
(13)

至此，通过流程图中系数1和系数2的对比，可以得出基于模态相关性系数的试验仿真结果差异。

3 缸内流场校核的结果分析

本研究数据来源由SIDI发动机的大涡模拟(LES)和粒子图像测速试验结果两部分组成。发动机转速为1 300 r/min，模拟的是部分负荷工况，进气压力为40 kPa。仿真基于CONVERGE 2.2 动态结构湍流模型进行计算，在去除第一个循环的基础上，共计算了50个循环的仿真结果。试验和仿真流场为图7所示的中心B-B平面，本研究以曲轴转角为270°为例进行分析。

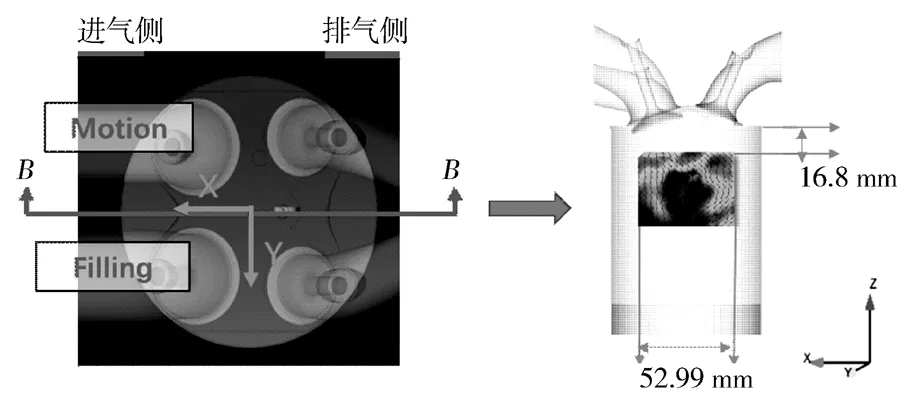
图7 试验和仿真流场平面示意

3.1 基于能量校核的结果分析

对流场试验和仿真数据进行能量的校核，即为根据模态前的能量系数进行分析。对试验和仿真数据进行有序的混合，前50个为试验工况，后50个为仿真工况。混合后进行POD分析，得出第1模态试验和仿真的对应系数。图8示出第1模态两组系数的波动情况对比。

图8 试验和仿真数据的第1模态系数对比

由图8可见，仿真和试验的模态系数均为正值，说明其对应的模态结构具有一个相同的流动方向。仿真数据的第1模态系数平均值为290.69，标准差为21.76，对应的变异系数(COV)为7.49%；试验数据的第1模态系数平均值为253.53，标准差为29.92，对应的变异系数(COV)为11.8%。仿真的主导模态的能量偏高，但其对应的标准差和变异系数偏小，说明仿真的循环变动要小于试验的循环变动。

从系数平均值的对比上看，仿真值相对于试验值存在着12%左右的差异。这一方面与发动机本身性能有关，试验数据的波动性体现了发动机本身的循环间差异；另一方面，从试验和仿真对比的角度来讲，仿真结果需要通过调整参数等方法来确保仿真结果的模态系数和试验结果更为接近，进而增强仿真结果的说服力。

图9示出模态2，3的试验和仿真系数对比。从物理意义上讲，除了包含大多数能量的第1模态，其他模态在一定程度上体现了较小的涡团结构特征。为了更直观地说明，图10示出了试验和仿真结果中某个循环的实际流场图。不难发现，除了左侧流场，尤其是左上侧体现缸内流场进气流态之外，其他的区域存在着较小的涡团结构，而这些小涡团结构又存在着极大的差别。秦文瑾等[15]指出，模态2显示的流场结构整体性明显下降．而局部小涡团则明显增多，模态3中该现象更加明显。说明模态越高，捕获局部随机脉动小涡团的能力越强。图10中的圆圈部分的次级涡团结构是模态2，3的主要特征点。从模态系数趋势和区别上来看，模态2的能量系数在量级上是很接近的，但小涡团模态的方向却是相反的，这一点与很多因素有关，如对第1模态结果的补偿，对圆圈部分次级涡团结构的捕获等。模态3的系数对于仿真和试验均具有随机性，体现了高阶小涡团的无序性。

图9 试验和仿真数据的第2，3模态系数对比

图10 试验和仿真单循环的速度场矢量图

3.2 基于模态相关性校核的结果分析

从模态间相关系数的角度来分析，分别计算了试验50个循环，仿真50个循环，混合100个循环这3种情况的POD结果。取试验和仿真50个循环的平均流场，绘制流场速度场(见图11a和图11b),展示试验和仿真流场的形态差异。为了进一步量化这种差异，依照基于模态相关性校核的思路和方法，对试验、仿真、混合的POD主要模态进行分析。

以混合POD的100个模态为基准，选取前5个模态，分别与仿真和试验的前5个模态进行相关性分析，进而比较其相关性系数。图11c,11d,11e分别为试验、仿真、混合三者的第1模态差异，用以形象化理解该方法结果分析的含义。混合流场的第1模态在流场的左上和左下有明显的大速度区域，而试验的第1模态侧重体现左下的大速度区域，仿真的第1模态侧重体现左上的大速度区域，图11c,11d,11e的形态也验证了图8中仿真的第1模态系数平均值要大于试验的第1模态系数平均值。这种方法对于前5个模态的相关性分析，实质上是在讨论相比等权重的混合POD，试验和仿真单独的POD流场模态所占的权重。理想情况下，这两个相关性系数应该都接近1或者其他临界数(视不同相关性系数定义)，而实际情况下，两个系数与1的差异以及两个系数间的差异体现了试验和仿真流场的差异。

图11 试验和仿真平均流场以及POD第1模态流场矢量

进一步对试验、仿真、混合的主要模态分别进行相关性计算，得出前面在模态校核流程中提到的系数1和系数2(见表2)。SI,MI的系数差异体现了试验和仿真的差异,由于本征正交分解过程中，模态只保留了结构信息，不包含能量信息，因此，KER的值为1,MI*与1的差值在10-6左右。通过这种全局分析的方法能够得到流场主要模态的差异，进而展现了流场结构的差异。这种方法实质上是在等权重的混合POD下，试验和仿真单独的POD流场所占的权重。系数1，2的理论值是1，并且接近1的程度和两个系数之间的差异体现了试验和仿真结果的差异。因此，可以基于某一个相关性系数(如SI)建立例如

(14)

这样的基准数，通过极其大量的试验，去挖掘得出普适意义上的临界值。其中，Indexexp，Indexsim为试验和仿真的某一种相关性系数，用以构建能明确化仿真模型适用范围的基准数。在基准数的某一个范围内，认为试验和仿真结果接近，可接受；在另外一个基准数的范围，则认定试验和仿真结果匹配精确度高。这样的工作是可行的并且对于试验和仿真差异的界定具有极大的意义。

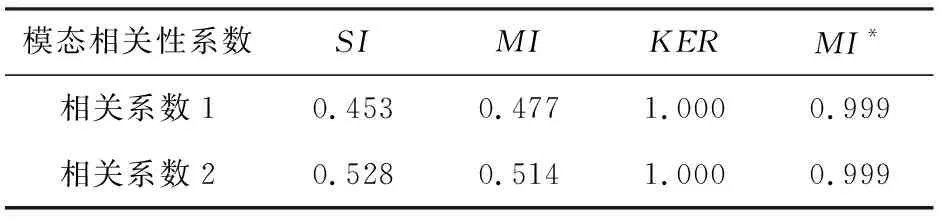
表2 模态相关性系数(系数1和系数2)

4 结束语

结合PCA(主成分分析)信号分析的角度，深入推导并剖析了本征正交分解在处理缸内流场过程中的物理意义，阐述了发动机缸内流场的主要模态实际上是原始流场经过“去除冗余的维度”和“降噪”的结果，对应于协方差矩阵对角线较大的方差值，即能量。提出并分析了能量和模态相关性两个方面的校核方法，其中创新性地提出了从模态相关性角度的计算方法和思路，对于过去仅从能量方面分析主要模态的系数，是一种合理的补充，有利于大涡模拟结果的全面校核。

基于高速粒子图像测速和大涡模拟数值计算的结果，对发动机缸内流场进行了模态和能量角度的校核分析。一方面，分析了发动机缸内流场大涡模拟和试验结果的主要模态的系数波动，模态1的系数差异体现了包含大部分能量的流场结构上的试验和仿真的差异，模态2，3的系数差异体现了局部小涡团的特征差异。另一方面，结合缸内流场速度矢量图、主要模态的相关性系数进行了定性和定量的分析。相关性系数体现的是等权重的混合POD下，试验和仿真单独的POD流场模态所占的权重。两个相关性系数的值的大小和差值，可以有效地体现仿真校核结果。

在模态相关性系数的校核方面，提出了进一步深化的方向，即试验，仿真模态的相关性系数1，2的大小本身以及差值，体现了试验仿真结果的客观差异，通过构建准则数，并基于大量实践，可以得出判断仿真结果优劣的准则数范围。这对于目前仿真结果可信度难以量化的情况，是一种可以考虑的实践思路。

参考文献：

[1] 蒋坚,高希彦.汽油缸内直喷式技术的研究与应用[J].内燃机工程,2003(5):39-44，58.

[2] 李相超,张玉银,许敏,等.直喷汽油机缸内喷雾湿壁问题研究[J].内燃机工程,2012,33(5):17-23.

[3] 田少雄,孔令逊,许敏,等.缸内涡流比对冷起动燃烧火焰的影响探究[J].内燃机工程,2017,38(3):1-8.

[4] 王天友,刘大明,张学恩,等.可变气门升程下汽油机缸内气体流动特性的研究[J].内燃机学报,2008,26(5):420-428.

[5] Sick V,Chen H,Abraham P S,et al.Proper-orthogonal decomposition analysis for engine research[C]//9th Congress,Gasoline Direct Injection Engines.Essen：[s.n.],2012:1-12.

[6] Lumley J L.The structure of inhomogeneous turbulent flows[J].Atmospheric turbulence and radio wave propagation,1967:166-178.

[7] Sirovich L.Turbulence and the dynamics of coherent structures.I.Coherent structures[J].Quarterly of applied mathematics,1987,45(3):561-571.

[8] 秦文瑾,许敏,孔令逊.直喷式汽油机缸内涡量场的本征正交分解[J].内燃机学报,2016,34(3):246-252.

[9] Fogleman M A.Low-dimensional models of internal combustion engine flows using the proper orthogonal decomposition[C]//Dissertation Abstracts International.[S.l.]：John L.Lumley,2005.

[10] 陈豪.直喷汽油机缸内过程稳定性机理的可视化研究[D].上海：上海交通大学,2014.

[11] Druault P,Guibert P,Alizon F.Use of proper orthogonal decomposition for time interpolation from PIV data[J].Experiments in Fluids,2005,39(6):1009-1023.

[12] Borée J.Extended proper orthogonal decomposition: a tool to analyse correlated events in turbulent flows[J].Experiments in Fluids,2003,35(2):188-192.

[13] Germano M,Piomelli U,Moin P,et al.A dynamic subgrid-scale eddy viscosity model[J].Physics of Fluids A:Fluid Dynamics,1991,3(7):1760-1765.

[14] Liu K,Haworth D C.Development and assessment of POD for analysis of turbulent flow in piston engines[C].SAE Paper 2011-01-0830.

[15] 秦文瑾.内燃机缸内湍流特性及其循环变动的大涡模拟与本征正交分解研究[D].大连：大连理工大学,2014.