大体积混凝土温度梯度及裂缝开展过程分析

雷元新，符耀东，朱 江

（佛山科学技术学院土木工程系，广东佛山528000）

1 工程概况

某建筑广场项目总用地面积81 101 m2，净用地面积59 591 m2，总建筑面积约540 000 m2。项目设地下室4层，建筑总高度150～180 m。4层地下室面积约20 000 m2，负4层地下室底板结构相对标高为-19.5 m，板底相对标高为-20.7 m。本工程地下室基础结构为“钻孔灌注桩+大体积承台+1 000厚底板”。由于本工程场地狭窄，结合该工程的道路设置情况，将地下室及裙楼施工划分为A、B、C共3个施工区段，3个区段依次进行流水施工作业，施工分区如图1所示。本项目施工现场环境比较复杂，基于现有资料及数据的完整性，现以C-1施工段中的CTA长方体承台进行分析，其尺寸为14.45 m×3.4 m×3.8 m，承台上面为1 m厚底板。

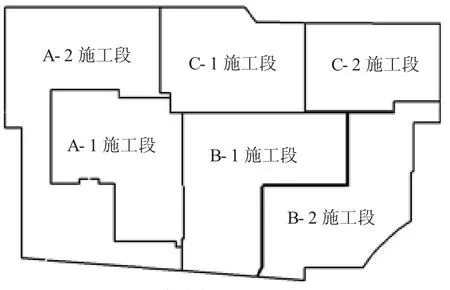
图1 地下室底板及承台施工分区图

2 计算参数的设定及模型的建立

2.1 有限元计算参数的设定

（1）材料参数

本次ANSYS分析采用SOLID70单元，混凝土及基础土体中比热、密度等材料属性赋值详见表1。

（2）大气温度及热生成函数

对于大气温度，可以通过当地就近气象台或者水文站获取该方面资料，有限元中大气温度变化可通过正弦或者余弦公式作为荷载施加到模型中［1-2］，如下式所示

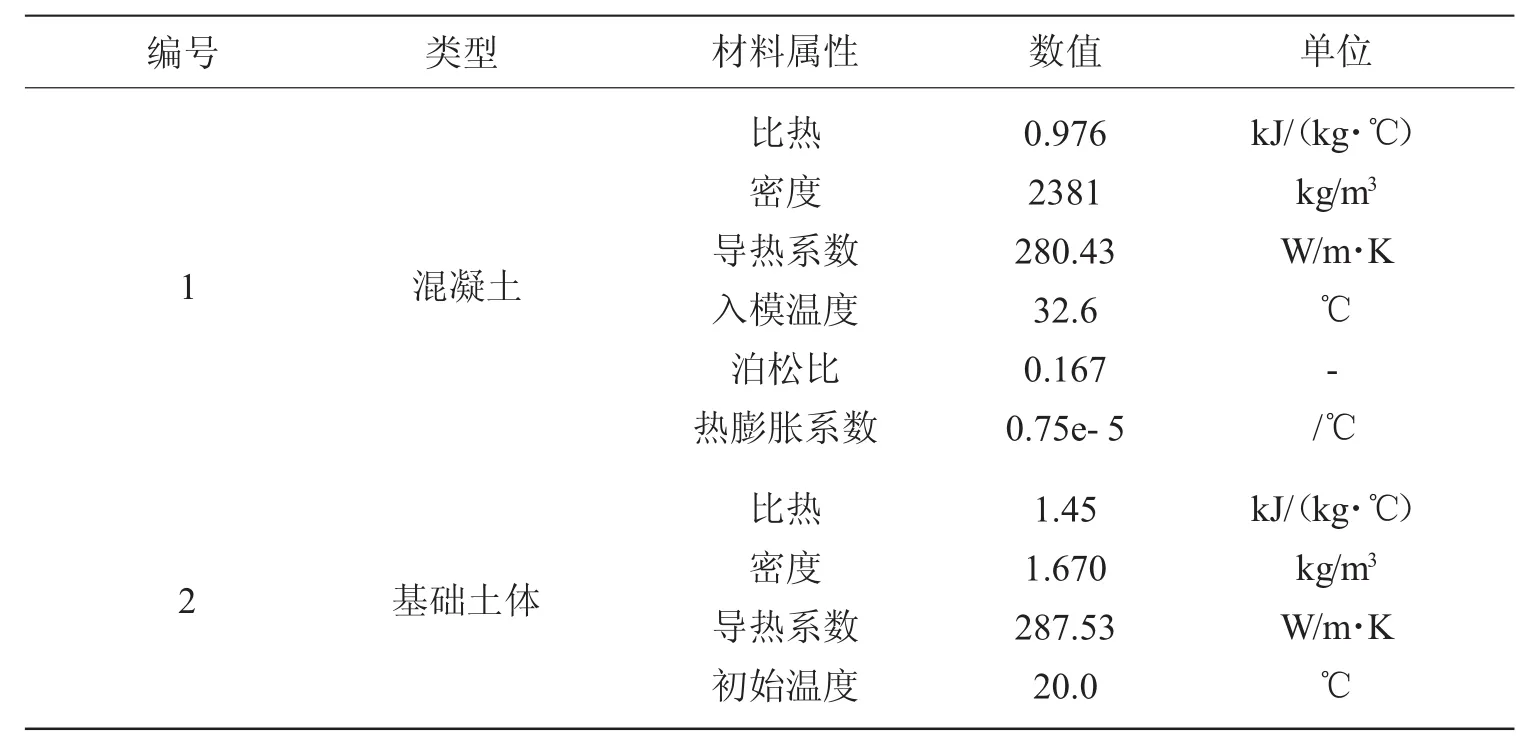
表1 ANSYS材料参数

式中，Ta指大气温度，单位℃；Tam指日平均气温，单位℃；Aa指大气温度日变幅，可取最高气温与最低气温之差的二分之一，单位℃；τ指时间，单位h；τ0指最高气温时间，单位h。

大体积混凝土温度主要热源是由水泥的水化热产生的，水化热可采用复合指数式表达［3］，如下式所示

式中，τ指龄期，单位h；Q（τ）=指混凝土龄期为τ时所积累的水化热，单位kJ/kg；Q0指τ→∞时混凝土最终的水化热，单位kJ/kg；a、b为常数。

将水化热通过生热率作为荷载施加到模型中［4］，生热率指混凝土在单位时间内产生的热量对时间的导数，如下式所示

式中，HGEN指生热率，单位W/m3；WC指单位体积混凝土水泥的用量，单位kg/m3。

将式（2）代入式（3）得

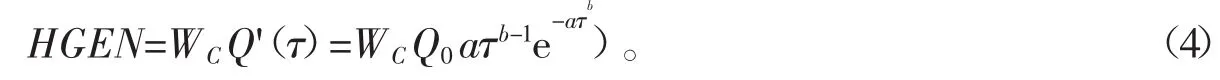
（3）弹性模量

大体积混凝土温度应力与弹性模量成正比关系，当混凝土入模后，其内部温度场的变化、水化热的散发以及弹性模量的增长都是同步发展，因此在有限元应力计算的过程中，考虑弹性模量与混凝土龄期的关系较为重要，C40混凝土弹性模量E（τ）随龄期τ变化［5］如式（5）所示

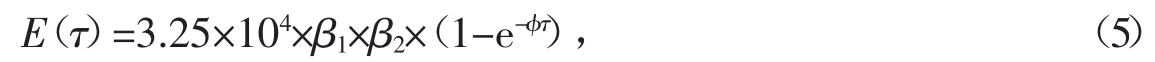
式中，φ为系数，可取0.09；β1、β2分别代表粉煤灰、矿粉掺量所对应的弹性模量调整修正系数，可按表2取值。

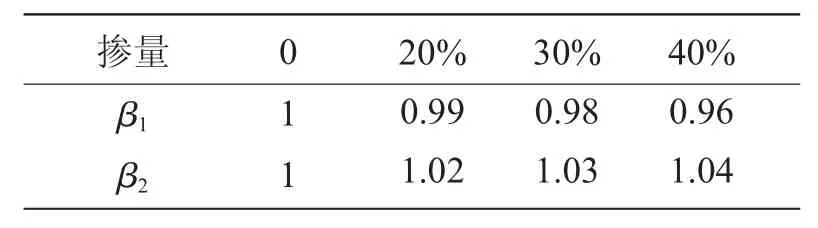
表2 粉煤灰及矿粉掺量掺合料弹性模量调整系数

2.2 有限元模型建立

所选大体积混凝土承台为规则的长方体，且四周边界条件相同，混凝土内、外温度分布具有对称性，故建立了1/4的模型进行模拟。承台上方为1 m厚的底板，四周及下方为10 m厚的基础土体，底板上表面与大气接触，下部为水泥砂浆护面胎模，承台与底板同时浇筑混凝土。对混凝土块体、基础土块体分别赋予表1中的材料属性，在提高单元网格精度的同时也要提高软件的计算速度，需要对主要部分单元进行高精度划分，对于次要部分单元可以简化网格划分，如图2所示。

图2 大体积混凝土有限元模型建立与网格划分

3 温度及应力场分析

利用ANSYS软件，确定好相关参数及边界条件，从混凝土入模开始，模拟20 d内混凝土温度场的变化情况，混凝土试块温度场分布情况如图3所示；由于篇幅问题，本文选取出现裂缝部分的混凝土，将其不同深度点处温度梯度与龄期的关系绘制成二维曲线图，如图4所示。

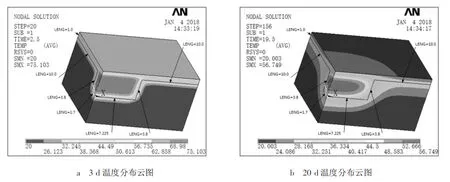
图3 CTA温度分布云图

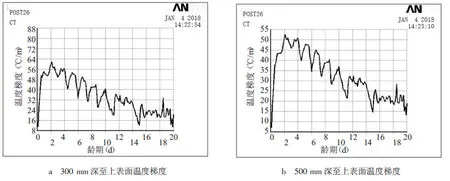
图4 CTA不同深度混凝土温度梯度

如图3所示，一定范围内，混凝土深度越大，其温度梯度越小，混凝土在3 d后，其最大内外温差接近40℃，到了20 d，混凝土内部温度最高仍超过50℃，内外温差多在20℃以下，但最高内外温差依然达到25℃。图4显示，混凝土浇筑1 d后，温度梯度迅速上升，2～4 d混凝土温度梯度处于最高阶段，其中300 mm处混凝土温度梯度最高达到62℃/m；混凝土中期，上表面混凝土受到大气温度的影响，使混凝土温度梯度出现较大幅度的变化，上层混凝土受到此影响表现更明显；混凝土在后期，整体温度梯度已下降到较小值。

4 ANSYS模拟裂缝过程分析

求解出混凝土温度场后，在ANSYS前处理阶段，根据式（5），每0.5 d取一次弹性模量，20 d内取40组弹性模量，采用APDL命令流方式输入到大体积混凝土模型；根据实验室测试混凝土立方体，所得出的3 d、7 d、14 d及28 d混凝土抗压强度，混凝土抗拉强度近似取抗压强度的十分之一值［6-9］；通过求解器计算出浇筑后20 d内混凝土裂纹发展过程，如图5～6所示。

图5 CTA第3 d裂纹

图6 CTA第7 d裂纹

图5～6中，由于温度梯度的变化，大体积混凝土出现裂缝。混凝土浇筑2 d后，CTA混凝土内外温差处于大于25℃状态，300 mm深处混凝土温度梯度达到60.0℃/m左右，500 mm深处混凝土温度梯度达到53.0℃/m左右，混凝土表面出现了裂缝，裂缝长度为45～120 mm；侧表面的混凝土温度梯度均小于32℃/m，并未出现裂缝。第7 d后，温度梯度下降到30～38℃/m，承台和底板的裂缝基本不再发展，但在上表面依然会有少许裂纹。由于混凝土上表面没有做保温养护的处理，而是直接与空气接触，混凝土上表面的热量与空气做热交换，承台内部温度分布较慢，大量的热量在短时间内并没有散发出来，形成了混凝土内外较大的温度梯度；由于混凝土内外温度梯度的变化，混凝土的拉应力也出现了较大变化，有限元模拟计算结果表明，混凝土浇筑3 d后，承台上表面的拉应力超过了现时混凝土的抗拉强度，导致了承台表面出现了几处裂缝；由于底板厚度相对承台较薄，其内部热量部分能散发出去，形成的内外温度梯度值并未导致混凝土出现裂缝，但也出现了一些裂纹，说明1 m厚的底板也需要做保温养护处理。

混凝土裂缝过程可按三阶段分析：

1）初始阶段的初始裂纹，混凝土浇注后，因水泥发生化学反应而产生大量的热量，在1～2 d混凝土内部温度迅速上升，为采取保温养护的混凝土上表面热量散发到大气中，形成内外大温度梯度，使混凝土体积出现变化而出现大拉应力，而此时混凝土弹性模量很小，在大拉应力状态下，混凝土会出现大应变，此时混凝土出现裂纹，并未开展成裂缝。

2）中期形成的裂缝，因水泥水化作用，中期混凝土内部温度依然出现缓慢上升，表面温度受大气温度影响较大，因内部温度下降与表面不稳定温度的变化，形成变化的温度梯度，当表面温度随大气温度下降较低时形成内外大温度梯度，此时的弹性模量已迅速增大，内部高温与外部低温的状态，其温度梯度超限时，裂纹就会扩展成裂缝。

3）后期混凝土内部温度处于缓慢下降状态，但由于此时混凝土徐变小，小温度梯度产生的温度应力使混凝土变形，混凝土受到自身及边界的约束作用，当这种变形不能释放时混凝土表面会出现裂纹。对于大体积混凝土来说，初期和中期裂缝的问题更为突出。

结果表明，有限元方法可以简易、有效地模拟大体积混凝土裂缝在温度应力下的发展过程。分析计算结果可以作为预测实际混凝土工程裂缝发展的依据。

3 结论

本文通过ANSYS软件计算出大体积混凝土温度场，模拟了在温度变化下混凝土裂缝的发展过程，得出以下结论：

1）实测与理论计算均说明，当混凝土内外温差超过25℃时，混凝土未必会开裂；而当大体积混凝土内外温差超过25℃，且内外温度梯度超过相应龄期温度梯度限值时，混凝土则出现开裂现象。

2）将混凝土裂缝发展情况分为三个阶段分析，早期和中期混凝土裂缝问题更为突出。

3）有限元方法可以有效地模拟混凝土块裂缝在温度应力下的发展情况，分析计算结果可以作为预测实际混凝土工程裂缝发展的依据。

［1］王新刚,高洪生,闻宝联.ANSYS计算大体积混凝土温度场的关键技术［J］.中国港湾建设,2009（1）:41-44.

［2］孙启冀,侍克斌,周峰.基于ANSYS的大体积混凝土温度应力计算程序开发研究［J］.电网与清洁能源,2015,31（5）:79-83.

［3］张子明,宋智通,石端学.混凝土绝热温升新理论及在龙滩工程中的应用［J］.红水河,2005,24（1）:5-10.

［4］丁兵勇,杨忠良,唐瑜莲,等.水电站厂房大体积混凝土温度应力分析与防裂措施［J］.南水北调与水利科技,2015,13（2）:362-365.

［5］中国冶金建筑协会.GB50496-2009大体积混凝土施工规范［M］.北京:中国计划出版社,2009.

［6］严俊,魏迎奇,蔡红,等.多场耦合下大体积混凝土初次蓄水的温度应力问题研究［J］.湖南大学学报（自然科学版）,2016,43（5）:30-38.

［7］FADUL M A A,MACKIE K R.Numerical Analysis of Coupled Heat and Mass Transfer Phenomena in Concrete at Elevated Temperatures［J］.Transport in Porous Media,2018（4）:1-22.

［8］刘大阴.超高层基础筏板大体积混凝土温度裂缝控制简［J］.施工技术,2015（S1）:442-447.

［9］史巍,侯景鹏.不同条件下相变控温大体积混凝土的温控性能［J］.建筑材料学报,2013,16（6）:1063-1066.