连续系统模型经离散化后的误差分析

杨 丹

（常州纺织服装职业技术学院，江苏 常州 213000）

随着计算机技术的迅猛发展，信息处理往往采用离散信号，而实际中大多为连续信号或模拟量。本文以二阶连续系统为例，研究采样周期对离散化方法精度的影响。

1 欧拉变换

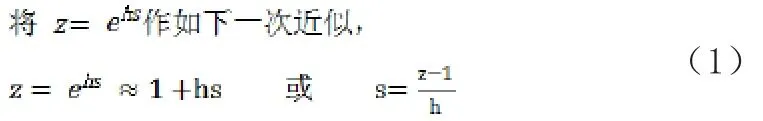
2 双线性变换

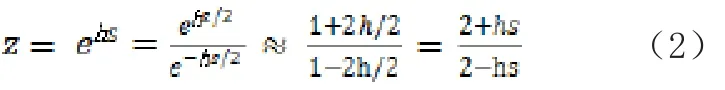
或

在进行模型转换时, 可以直接使用以上的离散化公式。

3 系统输出误差

以二阶系统传递函数模型为例，

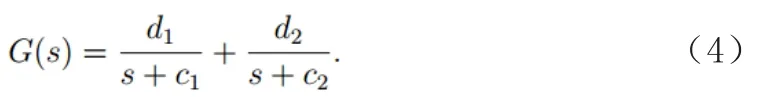
当系统输入为单位阶跃信号时，系统的时域输出为

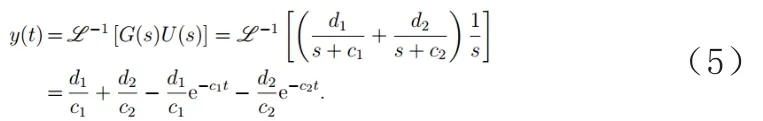
式（5）经欧拉变换离散化后得

输出误差

经双线性变换离散化后得

输出误差

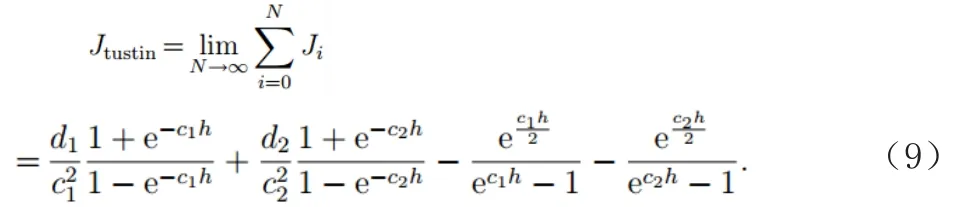
考虑以下二阶系统模型

当系统输入为单位阶跃信号时, 根据式（5）可知,系统的时域输出为

根据式（7）系统的输出误差为

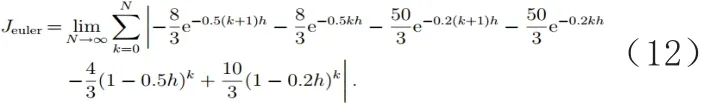
根据式（9）可知系统的输出误差为

当采样周期取时, 经欧拉变换和双线性变换离散化后的采样点处输出值与原连续曲线的关系如图1, 系统的输出误差如表1所示。

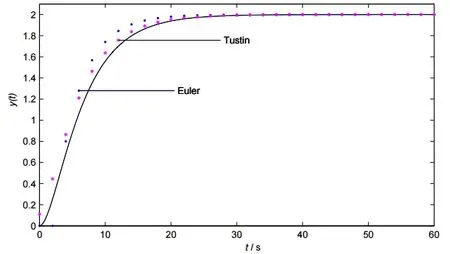
图1 h = 2时的连续响应曲线y(t)和离散采样点y(k)

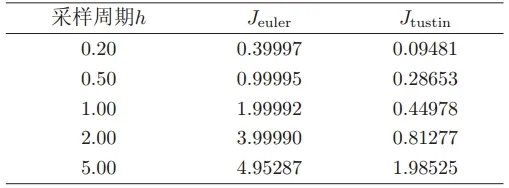
表1 误差与采样周期h之间的关系

4 结语

对于同一系统，单位阶跃为输入信号，同一种离散化方法的精度会随采样周期h的 变化而变化。h越小,离散化精度越高。反之，离散化精度越低。