基于弹流润滑及时变载荷分配模型的直齿轮效率研究
杨剑飞,陆凤霞,张沁薇,刘伟平
(南京航空航天大学 机电学院,江苏 南京 210016)
0 引言
齿轮传动作为一种重要的传动形式,广泛运用于汽车、航空等领域,其效率的计算也是国内外一直关注的热点。齿轮传动系统的功率损耗可分为有载荷功耗和无载荷功耗,其中有载荷功耗主要包括有载荷条件下的齿轮啮合功耗和轴承功耗,无载荷功耗主要包括齿轮及轴承的搅油损失、风阻损失。本文主要研究齿轮的啮合功耗。
传统的齿轮静态效率研究中,摩擦系数模型以及载荷分配模型对效率计算精度显得尤为重要,摩擦系数模型可分为平均摩擦系数模型及EHL摩擦系数模型,载荷分配模型可分为传统载荷分配模型(具有确定的载荷分配系数)以及时变载荷分配模型。
早期的学者Buckingham[1]、Merrit[2]、Niemann 和 Winter[3]基于沿啮合线上摩擦系数不发生变化以及齿面间载荷平均分配(单齿啮合区法向载荷Fn=2M1/(d1cosαw),双齿啮合区载荷分配系数为0.5)的模型,推导了几种齿轮啮合效率的计算公式,这也是ISO/TR 14179-1[4]、ISO/TR 14179-2[5](以下简称ISO-1、ISO-2)标准中齿轮啮合效率计算公式的来源。秦大同[6]基于平均摩擦系数模型及不同的齿轮载荷分配模型对行星齿轮啮合效率进行了分析。T Yada[7]抛弃了传统的齿面载荷分配模型,根据齿面摩擦系数从理论上重新推导了法向载荷的大小,得到时变载荷分配模型的齿轮效率计算公式,摩擦系数采用平均摩擦系数。文献[8]中介绍了部分基于一定试验的齿轮摩擦系数计算式,与早期的研究不同,这些摩擦系数随着齿轮啮合位置的变化也会发生变化,时变摩擦系数的出现对齿轮啮合效率的计算提供了一种新的思路。陈辛波[9-10]分别运用混合润滑状态下的摩擦系数公式及Benedict 和Kelley提出的齿轮摩擦系数经验公式,建立了直齿轮效率预测模型,模型中认为齿面间载荷平均分配。XU[11]基于弹流润滑理论,考虑齿面微观特性、润滑油非牛顿流体等特性,提出了精确的齿轮摩擦系数EHL计算模型,受到广泛的运用。
在过去的齿轮静态效率研究中,尚未见采用齿轮时变载荷分配模型和EHL摩擦系数模型结合的方法预测齿轮的啮合效率的文献。本文运用XU提出的EHL摩擦系数模型,结合直齿轮得啮合特性,考虑齿轮的法向载荷的时变性,建立一种新的直齿轮啮合效率预测模型。
1 齿轮啮合功耗数学模型
图1为齿轮外啮合的端面示意图,N1N2为理论啮合线,B1B2为实际啮合线,建立沿啮合线方向的坐标轴e,坐标原点为节点p。Ra1、Ra2为齿轮1、2的齿顶圆半径,Rw1、Rw2为齿轮1、2的节圆半径,Rb1、Rb2为齿轮1、2的基圆半径,ω1、ω2为齿轮1、2的角速度,αw为齿轮1、2的实际啮合角,x为啮入过程中的任意点,y为齿轮啮出过程中的任意点。
齿轮的啮合功率损耗包括滑动功率损耗和滚动功率损耗,后者在啮合功率损失中占的比例很小,一般可忽略。以一对齿从啮入到啮出为一个啮合周期,如图2所示,一个啮合周期内根据单双齿啮合可以将啮合线分为4段,B2C2,C2P,PC1,C1B1,其中B2C2、C1B1为双齿啮合区。

图2 单双齿啮合示意图
1.1 EHL摩擦系数模型
基于弹流润滑理论,考虑齿轮副表面粗糙度、润滑油非牛顿流体特性及热效应,Xu提出了齿轮副的摩擦系数计算模型:
(1)
式中:ν0为润滑油的动力粘度,单位为cps;ve为齿轮接触点处的卷吸速度,单位为m/s;R为接触点处的综合曲率半径,单位为m;S为表面粗糙度的均方根值,单位为μm。SR为滑滚比,f(SR,Ph,v0,s)可由式(2)计算得到:
f(SR,Ph,v0,S)=b1+b4|SR|Phlog10(v0)+b5e-|SR|Phlog10(v0)+b9eS
(2)
式中:b1,b2,…,b9的值依次在表1中给出。

表1 摩擦系数计算相关系数
1.2 时变载荷分配数学模型
时变载荷分配模型指的是抛弃齿面载荷分配模型,在齿轮的受力平衡方程中考虑摩擦力的影响,主动齿轮的输入力矩由主动轮上参与啮合的轮齿的法向压力及摩擦力的合力承担。一个啮合周期内,齿轮的啮合存在单双齿交替的情况,假设在双齿啮合区,齿轮1的输入力矩M1由参与啮合的两个齿平均承担。
图3、图4为啮合过程中,齿轮1在啮入过程中点x、啮出过程中点y的受力示意图,μ为时变摩擦系数,根据摩擦角的定义,可知ρ=arctanμ,Fx、Fy分别为x、y点的合力,大小根据力矩平衡求得,Fn为齿面法向载荷。值得注意的是Fn值具有时变性,其大小由Fx及摩擦角ρ共同确定,μFn为时变齿面摩擦力。

图3 啮入过程中齿轮1载荷分配模型
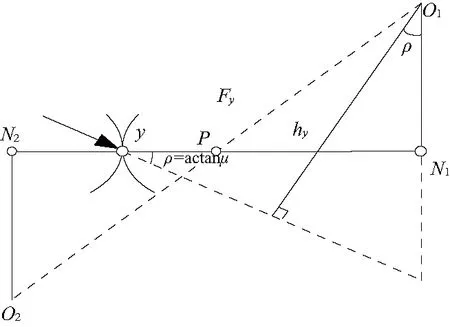
图4 啮出过程中齿轮1载荷分配模型
啮入过程中,根据力矩平衡,在单齿啮合区,齿轮1的输入力矩M1由该齿承担,那么式(3)成立:
(3)
式中,Fx1、Fnx1为单齿啮合区齿轮1受到的合力及法向载荷,hx是合力对齿轮1的力臂。
双齿啮合区,齿轮1的输入扭矩M1由双齿平均承担,那么有:
(4)
式中,Fx2、Fnx2为双齿啮合区齿轮1受到的合力及法向载荷。
同样,啮出过程中,单齿啮合区,有式(5)成立。
(5)
啮出过程中,双齿啮合区,有式(6)成立。
(6)
1.3 齿轮啮合效率的公式推导
如图1所示,沿啮合线方向建立坐标系,齿轮系统啮入过程中的输入功Wx1由式(7)得出:
(7)
式中,Tx1代表法向载荷Fnx、摩擦力μFnx对齿轮1的作用力矩。
齿轮系统啮入过程中的输出功Wx2由式(8)得出:
(8)
式中,Tx2代表法向载荷Fnx、摩擦力μFnx的反作用力对齿轮2的作用力矩。
齿轮系统啮出过程中的输入功Wy1由式(9)得出:
(9)
齿轮系统啮出过程中的输出功Wy2由式(10)得出

(10)
则时变载荷分配模型的一个周期的平均啮合效率η的计算式为:
(11)
2 仿真算例及对比验证
2.1 仿真对象的参数
为了验证新模型的有效性,分别运用Matlab对时变载荷分配模型、ISO-1、国标ISO-2的效率计算公式进行数值仿真,仿真对象采用来自于文献[11],具体参数如表2所示。

表2 仿真对象及相关参数
2.2 仿真结果及对比分析
由于试验条件有限,同样采用文献[11]中的试验数据,为了与试验数据形成对比,需要在本文的仿真结果、ISO标准中加入有载荷条件下的轴承功耗,单个轴承功耗计算公式如下:
PB=0.5μBWBdBω×10-3
(12)
式中,PB为有载荷条件下的轴承功耗,kW;μB为轴承摩擦系数,取0.001 1;WB为轴承径向载荷,N;dB为轴承内径(dB=30mm),ωb为轴承角速度,rad/s。
所以最终齿轮副啮合效率ηm为
(13)
式中,n为轴承的个数,PD为输入功率。
将试验结果、时变载荷分配模型啮合效率仿真结果、ISO-1、ISO-2中齿轮啮合效率的仿真结果进行对比分析,仿真结果如图5所示。


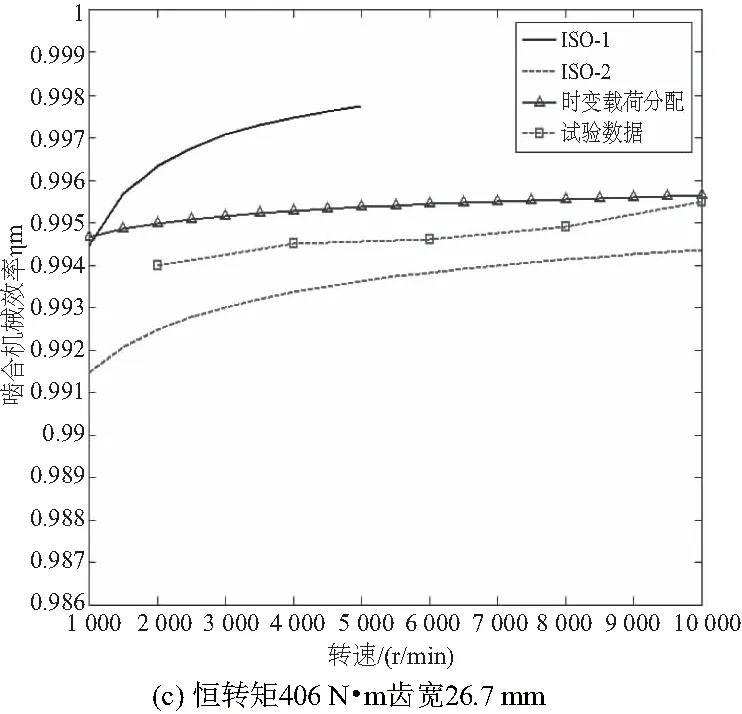

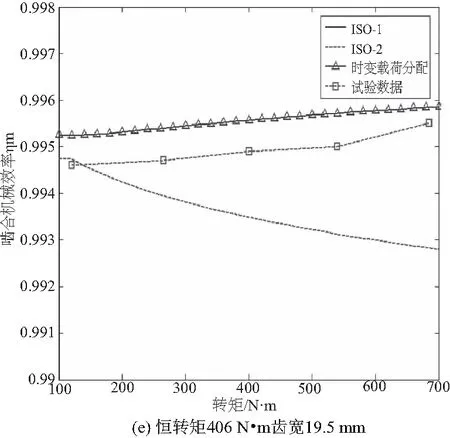
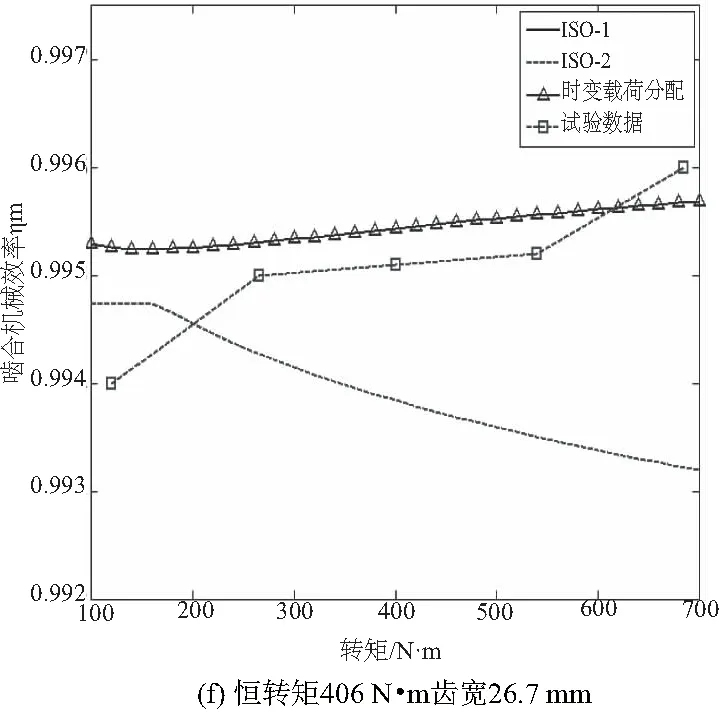
图5 时变载荷分配模型、ISO-1、ISO-2、试验数据对比
在该齿轮参数下,若齿轮转速超过5 000r/min,工况便超出ISO-1的计算范围,所以图5(a)-图5(f)中ISO-1标准对应的仿真数据只有一部分或者没有。
从图5还可以明显看出,时变载荷模型对效率的预测准确性要高于ISO-1、ISO-2。在恒转速6 000 r/min情况下标准ISO-2对效率的预测为:随着转矩的增大,齿轮啮合效率逐渐降低;时变载荷模型的预测为:随着转矩的增大,齿轮啮合效率也逐渐增大,与试验结果趋势基本一致。
两者的结论完全相反,原因是,在恒转速情况下,转矩的增大,齿轮端面上法向载荷也会增大。那么根据标准ISO-2摩擦系数公式计算得出的摩擦系数也会增大,直接导致标准ISO-2计算出的效率会减小,而图6反映了EHL摩擦系数模型下,恒转速6 000 r/min,转矩分别265 N·m、540 N·m、685 N·m时,齿轮副沿啮合线的摩擦系数分布情况,几乎在整个双齿啮合区域,摩擦系数随着扭矩的增大而减小,只有在节点附近区域,摩擦系数随着转矩的增大而增大。由于双齿啮合区域齿轮副相对滑动速度较大,啮合损失贡献最多,所以最终的趋势显示随着转矩的增大,啮合机械效率也会变大。对比结果显示,时变载荷分配模型对效率的预测具有较高的准确性,具有工程应用价值。

图6 恒转速6 000 r/min不同转矩下沿啮合线的摩擦系数分布
3 结语
提出了一种基于弹流润滑及时变载荷分配模型的直x齿轮效率计算方法,将仿真数据、试验数值、ISO-1数据、ISO-2数据进行对比分析,结果表明,基于该模型的计算方法与试验数据在数值上及趋势上均具有很好的一致性。
[1] Merritt H.E. Gears[M]. [S.I]Sir Isaac Pitman & Sons ,1946: 339-345.
[2] EarleBuckingham. Analytical Mechanics of Gears[M]. [S.I]McGraw Hill Book Company Inc,1949: 395-406.
[3] G..尼曼, H.温特尔机械零件(第二卷)[M]. 北京:机械工业出版社,1983.
[4] ISO/TR 14179-1:2001. Gears-thermal capacity-part1: rating gear drives with thermal equilibrium at 95 Csump temperature[S].
[5] ISO/TR 14179-2: 2001. Gears-thermal capacity-part2: thermal load-carrying capacity[S].
[6] 崔丽, 秦大同, 石万凯. 行星齿轮传动啮合效率分析[J]. 重庆大学学报(自然科学版), 2006, 29(3):11-14.
[7] Yada T. Review of Gear Efficiency Equation and Force Treatment[J]. Jsme International Journal, 1997, 40(1):1-8.
[8] 丁有永, 朱如鹏, 李政民卿. 乏油润滑直齿轮传动瞬态温度场主要影响因素分析[J]. 机械制造与自动化, 2013, 42(5):40-43.
[9] Xu H, Kahraman A,Anderson N E, et al. Prediction of Mechanical Efficiency of Parallel-Axis Gear Pairs[J]. Journal of Mechanical Design, 2007, 129(1):58-68.
[10] 陈辛波, 卢志坚. 基于弹流润滑的直齿轮动态效率模型及验证[J]. 同济大学学报(自然科学版),2013,41(5):773-778.
[11] 王斌, 陈辛波. 混合润滑状态下渐开线直齿轮啮合效率分析[J]. 同济大学学报(自然科学版), 2014, 42(12):1904-1911.
[12] XU H. Development of a generalized mechanical efficiency prediction methodology for gear pairs[D].Columbus: Ohio State University, 2005.

