基于最小二乘支持向量机左右逆协同的无人机解耦控制

许春山

(亿嘉和科技股份有限公司上海分公司，上海 200050)

无人机(unmanned aerial vehicle，UAV)具有成本低、灵活性高等特点，目前广泛应用于航拍测绘[1]、物流运输、农用植保[2]、灾害监测[3]和电力巡检[4]等领域，特别是在军事侦察领域优势突出[5]。对无人机飞行轨迹的精确跟踪，是无人机实现任务多样性的重要保障。但由于无人机本身具有多变量、非线性强耦合的特性，又易于受到外界环境的干扰，因此研究无人机系统的解耦控制变得至关重要。

目前国内外学者对无人机解耦控制做了相关研究。曾加等[6]通过非线性动态解耦研究了无人机的直接力控制问题。陈澜等[7]提出一种基于定量反馈理论的无人机解耦控制方法，可以较好地实现解耦，但采用的QFT鲁棒控制器受稳定平台参数影响。陈金科等[8]通过引入自抗扰控制器实现了对速度回路与俯仰角回路的解耦控制。许江涛等[9]针对无人机飞行过程中横侧向运动非方阵系统模型，提出了一种新型的解耦方法。首先采用内环反馈方法对模型进行方阵化，提出基于最优化的逆乃奎斯特阵列法的扩展INA法，然后将该方法用于无人机非方阵系统的动态解耦补偿器求解。楼静梅等[10]针对无人机横侧向控制系统，利用自抗扰控制技术对无人机滚转通道和偏航通道进行解耦控制。ZHANG等[11]提出了基于稳定逆因果近似解的无人机空速/高度精确解耦跟踪。徐旻等[12]设计了自适应和前馈协同解耦控制器，实现对无人机机体俯仰角和滚转角的解耦控制，但控制器受前馈控制系统阶数影响。张迪洲等[13]根据总能量控制理论设计了过渡模式的在线解耦控制策略。屈高敏等[14]针对无人飞行器线性解耦控制中两种常见方法的不足，采用微分几何方法对其进行了解耦控制设计。右逆系统[15]是一种适用于一般线性化系统解耦的控制方法，具有理论严格、物理意义清晰、应用方便的特点，通常与支持向量机等智能算法结合使用，已经成功应用于电力系统控制[16]、机器人控制[17]、电机控制[18]等领域，解耦效果好，鲁棒性高。

本文选用右逆理论对无人机进行解耦。首先采用Interactor算法构建右逆系统，而右逆系统中会出现一个不可测变量，即旋翼桨叶总距俯仰角。该变量作为右逆系统的输入量(也称为状态反馈量)是构建右逆系统的关键，同时该变量作为无人机系统的输出，在进行闭环控制时需要对其测量。但由于目前测量设备受到经济和技术上的限制，实现上述变量的直接测量存在困难。为此可采用基于内含传感器左逆软测量的方法来获得不直接可测的输出变量，然后基于软测量结果，实现右逆解耦控制。

基于上述思路，本文提出了一种基于最小二乘支持向量机(LSSVM)左右逆协同的无人机解耦控制方法。首先根据Interactor算法，对无人机系统输出进行微分获得右逆系统，并证明其可逆性；同时根据内含传感器左逆原理得到无人机旋翼桨叶总距俯仰角，将其代入到右逆系统，构成左右逆协同控制器；然后利用最小二乘支持向量机建立右逆模型，并将其串联在原系统之前，与积分器共同构成伪线性复合系统实现无人机线性化与解耦；最后将PID与右逆系统结合构成左右逆复合控制器实现解耦控制。基于上述方法建立的模型物理意义直观清晰。本文以无人直升机模型为研究对象，仿真结果表明，所提方法能实现对无人直升机的精确控制，且具有较强的鲁棒性。

1 无人直升机数学模型

无人直升机复杂的动力学特性决定了其控制系统是一个多输入多输出的系统，具有较强的非线性。旋翼是无人直升机的主要运动部件，对无人机的运动控制主要是通过桨毂对旋翼的变距操纵实现的，操纵与响应之间具有较强的耦合性。无人直升机的动力学模型[19]为：

(1)

将式(1)写成标准形式：

(2)

2 无人机数学模型可逆性分析

2.1 右逆方法

定义:给定系统Π：u→y，如果存在一个相应的系统Πr：v→r，在系统Πr的初值条件满足系统Π的初值条件的情况下，当u(t)=r(t)时，如果等式y(t)=v(t)成立，则称系统Πr为系统Π的右逆系统，系统Π为右可逆的。

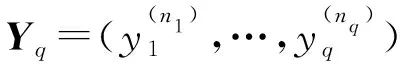
(3)

(4)

2.2 可逆性分析

Step1，对y1求一阶导数，根据式(2)可得：

(5)

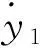
a6x4)1/2x3]u1

(6)

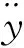
(7)

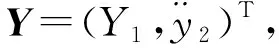
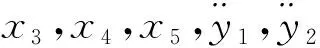
(8)

根据隐函数存在唯一性定理，右逆系统可表示为：

(9)

2.3 LSSVM右逆模型构建

式(9)表示的右逆系统模型是根据隐函数定理获得的，难以用解析表达式进行精确的描述，因此不利于右逆系统的实现。

y(x)=wTφ(x)+b

(10)

式中：w为权向量；b为偏置量，φ(•)为非线性映射。LSSVM可以更高的精度和正确率拟合非线性函数，可以适应未知或不确定的系统，帮助解决右逆系统中的非线性问题。

为了使样本拟合误差最小化，采用SRM(structure eisk minimization)准则，将回归问题变为约束优化问题：

(11)

式中：ei为松弛因子。根据泛函理论，本文采用满足Mercer条件的径向基函数作为核函数K(x(i),x)，将式(11)构造的Lagrange函数转变为无约束优化函数，最终得到LSSVM回归决策函数：

(12)

根据上述理论，选取垂直飞行速度、旋翼桨叶转速、旋翼桨叶总距俯仰角θ以及系统输出的二阶导数作为右逆系统输入，原系统输入作为右逆系统输出，采用LSSVM和积分器来构造直升机右逆控制模型。经过数据严格训练得到无人直升机垂直飞行速度和旋翼桨叶总距俯仰角θ的线性化右逆模型，将其串联在原系统之前构成2阶伪线性复合系统，如图1所示。

图1 基于LSSVM的无人机右逆系统

当对无人机进行闭环控制时，系统中的桨叶总距俯仰角θ作为输出反馈量和状态量是无法进行直接测量的，因此这里采用基于内含传感器逆的动态软测量方法，实现对桨叶总距俯仰角θ的间接测量。该策略通过逆系统理论计算得到无人直升机姿态的左逆模型，并利用支持向量机逼近非线性函数，辨识左逆模型，实现对桨叶总距俯仰角θ的软测量。

3 左右逆协同控制

3.1 左逆软测量方法

系统具有左可逆性是指系统的输入总可以通过一个左逆系统的输出得到还原。通过对原系统内部的内含传感器进行可逆性原理证明，并根据隐函数存在唯一性定理可推导出左逆系统。

(13)

如果所建立的内含传感器左可逆，则通过推导可得到其左逆系统，表达式为：

(14)

3.2 左可逆性分析

图2 左逆软测量原理图

Step1，对z1求0阶导数，可得z1=x1，并定义t10=rank(∂(z1)/∂x)，显然t10等于1。

(15)

Step3，对z1求2阶导数，可得

(16)

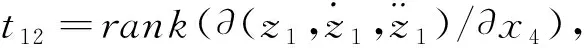
(17)

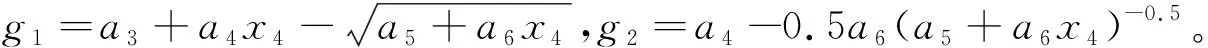
(18)

根据隐函数存在唯一性定理，将左逆表示为：

(19)

由此证明无人直升机飞行控制系统的左逆存在。

3.3 左右逆协同控制模型

通过分析系统的左可逆性，构造出左逆系统的内含传感器，实现对总距俯仰角θ的间接测量。将内含传感器应用到建立的无人直升机右逆系统中，得到如图3所示的无人直升机左右逆协同控制模型。

图3 无人机左右逆协同控制系统

4 仿真验证

4.1 无人机复合控制器

3节推导出了无人直升机的左右逆协同控制模型，利用左逆系统对不可测量的θ进行软测量，并采用右逆系统进行输出量的线性化解耦。为了更好地实现对无人直升机桨叶总距俯仰角和垂直飞行速度的解耦控制，引入PID(比例、积分、微分)控制器，构造基于无人直升机左右逆协同控制模型的复合控制器，原理如图4所示。

图4 无人机复合控制器

利用PID控制器实现对整个控制系统的闭环控制，提升了无人直升机控制系统的性能。

4.2 仿真参数

为了验证本文最小二乘支持向量左右逆协同解耦控制系统在无人直升机控制方面的有效性，在MATLAB环境下做了仿真研究。无人直升机中的相关参数标称值见表1。

表1 无人直升机模型参数

在MATLAB中构造无人直升机模型，当无人直升机稳定运行时，在特定的时间上施加激励信号，分析系统对激励信号的响应性能，并与其他控制器进行对比，验证本文方法的有效性。

4.3 结果分析

对LSSVM左右逆协同解耦控制进行仿真测试，并将结果与基于动态逆和滑模的无人直升机飞行解耦控制进行对比，图5和图6分别为无人直升机垂直飞行速度以及桨叶总距俯仰角的动态响应。如图5所示，分别在0s、2s和6s时刻对系统施加阶跃信号。对比3种控制器，左右逆协同控制对于垂直飞行速度的阶跃响应相比于模糊控制响应速度更快，同时超调量也较小；对比动态逆控制，虽然超调量略大，但是在响应速度上优势明显。

图5 垂直飞行速度动态响应

如图6所示，对比3种控制方法的旋翼桨叶总距俯仰角动态响应，左右逆协同控制响应速度较快，超调量也较小，综合性能较好。

综合对比分析图5和图6的动态响应，左右逆协同解耦控制对无人直升机的垂直飞行速度以及桨叶总距俯仰角的解耦效果较为理想。垂直飞行速度分别在2s和6s时有阶跃信号，桨叶总距俯仰角在两个时刻都产生了波动，即耦合效应。但是，左右逆协同相比动态逆和模糊控制，总距俯仰角耦合波动较小，且能够更快地消除波动；同样，在4s和8s时，旋翼桨叶总距俯仰角均产生了阶跃响应，这两个时刻无人机垂直飞行速度也都产生了波动，左右逆协同对比其余两种方法，同样能够更快地消除垂直速度的波动，保证无人直升机的稳定运行。

图6 旋翼桨叶总距俯仰角动态响应

5 结束语

无人机飞行控制系统具有多变量、非线性强耦合的特点，其解耦控制易受内部状态量以及输出反馈量不可直接测量的影响，为此本文提出了一种基于最小二乘支持向量机左右逆协同的无人机解耦控制方法。该方法利用右逆实现无人机解耦控制，左逆实现内部状态量和输出反馈量的间接测量，同时结合最小二乘支持向量机算法完成左右逆模型的构建，整个过程理论推导严格，模型结构简单，物理意义直观清晰。仿真结果表明，所提方法对无人直升机飞行控制解耦性能高，鲁棒性好。

参考文献：

[1] 孙钰, 韩京冶, 陈志泊, 等. 基于深度学习的大棚及地膜农田无人机航拍监测方法[J]. 农业机械学报, 2018,49(2): 133-139.

[2] 杨艳, 王杰, 白正清, 等. 山西省农用植保无人飞机发展现状分析[J]. 中国农机化学报, 2017(2): 13-17.

[3] 胡可, 陈思思, 王俊伟. 无人机载红外载荷在应急测绘中的应用[J]. 测绘科学, 2015,40(10): 60-64.

[4] 麦晓明, 朱庄生, 彭向阳, 等. 多传感器无人机电力线路巡检 POS 系统[J]. 中国惯性技术学报, 2015,23(1): 20-28.

[5] 刘慧霞，马丽娜，李大健, 等. 无人机多机协同侦察系统关键技术[J]. 火力与指挥控制, 2017,42(12): 1-4.

[6] 曾加, 慕春棣. 非线性解耦控制在无人机中的应用[J]. 清华大学学报(自然科学版), 2005,45(4): 545-548.

[7] 陈澜, 吴梅, 安锦文. 无人侦察机目标跟踪系统鲁棒控制[J]. 测控技术, 2005,24(5): 58-60.

[8] 陈金科, 孙秀霞, 张力. 基于ADRC的无人机纵向通道控制[J]. 空军工程大学学报(自然科学版), 2006,7(6): 10-12.

[9] 许江涛, 崔乃刚, 路菲,等. 无人机非方阵系统解耦控制[J]. 航空学报, 2008,29(增刊1): 157-162.

[10] 楼静梅, 张科. 基于自抗扰理论的无人机横侧向解耦控制研究[J]. 计算机测量与控制,2014,22(4): 1152-1154.

[11] ZHANG Jianhong，ZHANG Ping. Precise decoupling tracking of airspeed and altitude for UAV based on causal solution of stable inversion[J]. Chinese Journal of Aeronautics, 2009,22(3):307-315.

[12] 徐旻, 吴炎烜, 王正杰, 等. 小型涵道风扇无人机自适应解耦控制律设计[J]. 北京理工大学学报, 2012,32(3): 235-238,301.

[13] 张迪洲, 陈自力, 胡永江. 尾坐式无人机过渡模式纵向解耦控制[J]. 系统工程与电子技术, 2018,40(1): 132-138.

[14] 屈高敏, 李继广. 基于微分几何方法的飞翼无人飞行器解耦飞行控制[J]. 弹箭与制导学报, 2018,37(3): 1-9.

[15] 戴先中，刘军，冯纯伯. 神经网络α阶逆系统在离散非线性系统控制中的应用[J]. 控制与决策,1997,12(3): 217-221.

[16] 戴先中，陈珩何丹. 神经网络逆系统及其在电力系统控制中的应用[J]. 电力系统自动化,2001,25(3):11-17.

[17] 徐庆宏, 黄家才, 周磊. 基于神经网络逆系统的机器人分数阶滑模控制[J]. 组合机床与自动化加工技术, 2015 (12):49-52.

[18] 刘欣欢, 徐桂芝, 刘旭. 永磁同步电机系统神经网络逆解耦控制[J]. 河北工业大学学报, 2017, 46(5):1-9.

[19] 段富海, 何长安, 章卫国, 等. 反馈线性化与连续滑模控制方法在直升机控制中的应用[J]. 西北工业大学学报, 2000，18(3): 378-381.