Re数对小尺寸离心叶轮模化设计的影响分析

王 鑫

(西安邮电大学计算机学院, 陕西 西安 710121)

随着节能减排要求的日益深化，离心压缩机作为石油、化工、冶金以及电力行业的主要耗能设备，不断地向高性能、高压比的方向发展[1-3]。离心叶轮作为离心压缩机的核心部件，其气动性能的优劣对整个压缩机级起着决定性的影响[1,4]。

在离心压缩机的设计中，常采用模化设计方法，其特点是根据一台性能好的模型级，利用相似原理来设计新的压缩机[5]。应用模化设计方法时，模化叶轮与原始叶轮之间需要满足进口速度三角形守恒、Re数(雷诺数)守恒和Ma数(马赫数)守恒才能保证叶轮的等熵效率不变。一般来说，除非进口气体温度或物性发生重大变化，Ma数都会自动满足守恒条件，但随着气体黏性(或压力)的变化，Re数会随着叶轮几何尺寸的缩小而减小。对于大尺寸叶轮，Re数的影响较小，并且在用模化设计时常常忽略其影响，但随着叶轮几何尺寸的缩小，则必须考虑Re数对叶轮模化设计的影响。

本文利用相似原理，将叶轮外径为60mm的小尺寸离心叶轮分别缩小及放大了5倍，得到相应的模化叶轮。在模化设计过程中，叶轮进口总温及总压保持不变，调整模化叶轮的转速和进口质量流量，保证叶轮进口速度三角形守恒及Ma数守恒。以原始叶轮等熵效率作为参考，本文得到了该小尺寸离心叶轮效率损失和雷诺数之间的指数关系式，通过比较绝热条件下缩小叶轮及放大叶轮指数n的大小，研究了Re数对小尺寸离心叶轮模化设计的影响，并对叶轮内部流动进行了分析。

1 研究方法

1.1 研究对象

本文以外径为60mm的小尺寸离心叶轮为研究对象，该叶轮叶片形状通过求解给定角动量分布的S2流面逆命题方法得到。利用相似原理，将此叶轮分别缩小及放大5倍，得到了相应的模化叶轮，表1给出了原始叶轮与模化叶轮的相关几何参数及Re数数值，Re数由叶轮圆周速度、叶轮外径和进口气体黏性系数定义。

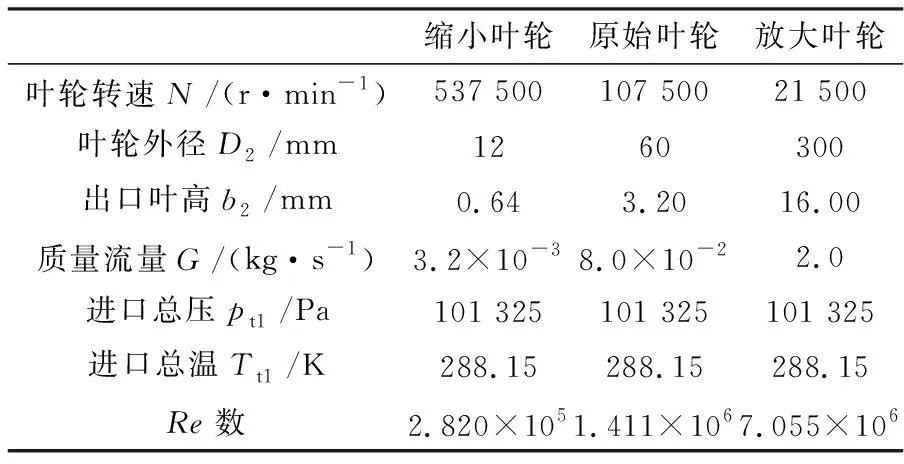
表1 原始叶轮及模化叶轮几何参数

1.2 数值计算方法

在数值计算中，本文将包括叶轮进口段、出口段及叶顶间隙区域的一个叶轮通道作为计算区域，考虑到网格数目与计算结果的独立性，最终确定的计算网格包含约60万个网格节点，并对叶轮叶片近壁面、端壁、前缘和尾缘等流动复杂区域进行网格局部加密。

采用计算流体动力学(CFD)方法计算叶轮内部湍流Navier-Stokes方程组，湍流模型选择Spalart-Allmaras模型，数值方法采用基于时间推进的数值离散格式，空间差分采用中心差分格式，为保证计算收敛，添加了人工黏性系数，采用多重网格方法、变时间步长和隐式残差光顺方法加速收敛。

计算区域进口给定总温、总压，沿叶轮轴向进气，出口给定叶轮质量流量，与叶轮相关的网格块和叶轮壁面给定转速，固体壁面采用绝热无滑移边界条件，采用定常计算方法计算叶轮内部流动。

2 结果与讨论

2.1 Re数对叶轮总体性能的影响

在确定的流动条件下，Re数定义了惯性力和黏性力的比值，并且表征了由于黏性效应引起的效率损失的大小。在模化设计中，Re数常常作为研究几何尺寸变化和性能变化之间关系的一个比例因子。图1给出了壁面绝热条件下原始叶轮和模化叶轮等熵效率的计算结果，由图可见：放大叶轮的等熵效率要高于原始叶轮，缩小叶轮的等熵效率要低于原始叶轮，但峰值效率点的位置并没有发生变化。由图中还可以发现，放大叶轮与原始叶轮的效率差值随着质量流量的增大而增加，而缩小叶轮与原始叶轮的效率差值随着质量流量的变化并无明显规律可寻。

图1 原始叶轮与模化叶轮等熵效率对比

叶轮效率损失(1-η)和Re数之间存在如下的经验公式：

(1)

式中：η为叶轮等熵效率；Re为叶轮雷诺数；D为叶轮外径；下标ref表示参考值。表2给出了设计流量下的具体计算结果，由表可以看出：相比于原始叶轮，放大叶轮的效率变化(绝对值)要高于缩小叶轮的效率变化(绝对值)；对于放大叶轮，指数n也稍大一些，因此在模化设计过程中，Re数对于放大叶轮的影响更显著一些。

表2 设计点叶轮等熵效率计算结果及对比

如前所述，不同流量下的效率变化也是不同的，因此指数n也是质量流量的函数。例如，对于放大叶轮，不同流量下的指数n的数值如下：

2.2 设计点叶轮内流动分析

图2给出了设计流量点沿叶轮叶片50%叶高展向截面相对Ma数等值线图，由图可见：模化叶轮与原始叶轮有着相似的Ma数分布，但随着叶轮几何尺寸的缩小，Re数减小，叶轮叶片表面边界层增厚，同时尾迹区变大，这意味着近壁面流动更容易发生分离，黏性损失也随之增大；另一个明显的变化是随着叶轮几何尺寸的减小，叶轮流道中部及后部低相对Ma数区域范围扩大。

图2 50%叶高展向截面相对Ma数等值线图

3 结束语

本文对小尺寸离心叶轮模化设计理论进行了数值研究，重点考察了Re数对模化设计过程的影响。研究结果表明：放大叶轮的等熵效率要高于原始叶轮，而缩小叶轮的等熵效率要低于原始叶轮。

文中获得了该小尺寸离心叶轮效率损失和Re数之间的指数关系式，并对放大叶轮及缩小叶轮进行了对比分析，结果表明：对于放大叶轮，指数n的数值要高于缩小叶轮，Re数在模化设计过程中的影响更显著一些。进一步对叶轮内部的流动分析表明：Re数的下降意味着更厚的边界层和范围更大的尾迹区，叶轮壁面内的流动更容易发生分离，黏性损失也随之增加。

本文的研究主要针对小尺寸离心叶轮模化设计方法的数值研究方面，进一步的研究工作是对该模化设计方法的实验验证与分析。

参考文献:

[1] YAMADA K, TAMAGAWA Y, FUKUSHIMA H, et al. Comparative study on tip clearance flow fields in two types of transonic centrifugal compressor impeller with splitter blades[C]// ASME Turbo Expo 2010: Power for Land, Sea, and Air. New York, USA：ASME Press，2010:2053-2063.

[2] LEIBFRIED D, SCHIRRMACHER A, BARTELMANN M, et al. The effect of leading-edge geometry on wake interactions in compressors[C]// ASME Turbo Expo 2009: Power for Land, Sea, and Air. New York, USA：ASME Press，2009:1769-1779.

[3] 李紫良,卢新根,张燕峰,等.高压比离心压气机串列叶轮内部流动机理研究[J].推进技术,2017,38(10):2393-2400.

[4] 刘正先,陈丽英.亚声速半开式离心叶轮叶顶间隙的流动特征[J].航空动力学报,2012,27(4):937-945.

[5] 祁大同.离心压缩机原理[M].北京：机械工业出版社,2018.