锂离子电池温度变化过程仿真与验证

马 龙，文 华



锂离子电池温度变化过程仿真与验证

马 龙，文 华

（南昌大学机电工程学院，江西 南昌 330031）

针对软包锂离子电池放电过程中温度变化过程进行研究，依据电池产热基本理论，通过内阻实验及0.5 C放电倍率下的温升实验计算出瞬态生热率曲线，得出电池熵热系数，建立生热速率随放电深度不断变化的瞬态生热模型，基于该模型进行不同放电倍率的温度仿真模拟，并与实验进行对比。结果表明，温度变化模拟结果与实验相吻合，生热率变化模拟结果与实验计算值相符合，模型可以很好地模拟电池在不同放电倍率下的温度变化，对电池温升过程分析及电池热管理过程控制具有指导意义。

锂离子电池；热特性；熵热系数；温度变化

随着国家对新能源汽车行业的重视与引导，我国锂离子电池行业的规模得到迅猛发展，目前已经超越韩国和日本，跃居全球首位。锂离子电池具有工作电压高、能量密度大、循环寿命长、单体额定电压高，自放电率低等优点，已经成为动力电池的首选。锂离子动力电池在放电过程中会产生大量的热，导致温度的上升，影响到电池本身的充放电性能与循环寿命，严重时会涉及其安全性与可靠性[1]，不少学者已经对电池的产热机理和产热模型进行了深入的研究分析，但是针对电池在不同放电倍率下的瞬态生热很少涉及，这对分析电池放热量以及放电过程温度变化有指导意义。

目前根据锂离子电池产热模型方面发展，按照产热原理可以分为电化学-热耦合模型、电-热耦合模型和热滥用模型[2]。电化学-热耦合模型是从电化学反应生热的角度建立的热模型，使用最广泛的是BERNARDI等[3]在1985年提出的电池生热基本理论，将电池生热分为可逆反应热（熵热）和不可逆热[过电压（-）引起的][4]，其中不可逆热包含电池的极化热和欧姆内阻产热[5]。很多学者对Bernardi生热速率0模型进行进一步研究和分析，构建了不同维度的生热模型，如集中质量模型、一维模型、二维模型、三维模型。电-热耦合模型是根据电池内部的电流密度分布建立的热模型，多使用在二维或三维温度场分析，便于改进电池外型、极耳、集流体等的设计以及研究电池的一致性问题[2]。热滥用模型是为了研究电池在热滥用条件下达到失控状态时的变化，一般是在传统热模型的基础上耦合内部的生热反应。

根据Bernardi电池生热理论公式简化得到的集中质量模型，电池生热中的欧姆内阻产热和极化热可以通过内阻测试并计算得到[1]，比较难以确定的是可逆反应热部分，影响可逆反应热变化的是熵热系数（d/d）。目前很多学者进行了关于熵热系数的分析和研究，研究方法有直接测量法、可逆热等值法、极化热扣除法3种[6]。直接测量法[7]需要大量测试时间，测量结果的精度也会受到影响。本文通过0.5 C放电倍率下的电池绝热温升实验计算出电池生热率曲线，并根据极化热扣除法扣除不可逆热部分求出可逆反应热，计算出瞬态熵热系数。根据电池内阻随温度和DOD的变化关系，以及熵热系数随DOD的变化关系，建立了生热率随时间不断变化的集中质量生热模型，模拟不同放电倍率下的温度变化。仿真结果与实验相符合，表明其能够模拟电池单体在放电过程的温度场变化，特别是针对小倍率放电中期的温度场变化比较明显，为电池单体热仿真和电池包热管理的过程控制提供指导。

1 实 验

1.1 研究对象

以某公司生产的软包锂离子动力电池单体为研究对象，如图1所示，电池规格参数见表1。电池单体层叠部分厚度为8 mm，正极极耳厚度为0.5 mm，负极极耳厚度为0.3 mm。实验设备包括动力电池测试系统、高低温防爆实验箱、多路温度测量仪等。

图1 锂离子电池单体

表1 锂离子电池规格参数

1.2 实验测试

1.2.1 内阻测试

关于电池的内阻测试的方法有很多，其中混合脉冲功率特性测试方法（hybrid pulse power characterization，HPPC）测试方法简单快捷，较其它方法有明显优势[8]。本实验采用HPPC测试方法测试在不同环境温度下的放电内阻，温度范围为-10～50 ℃，实验过程每隔1 s记录一次。测量结果见图2，横坐标为放电深度（depth of discharge，DOD），纵坐标为放电内阻。

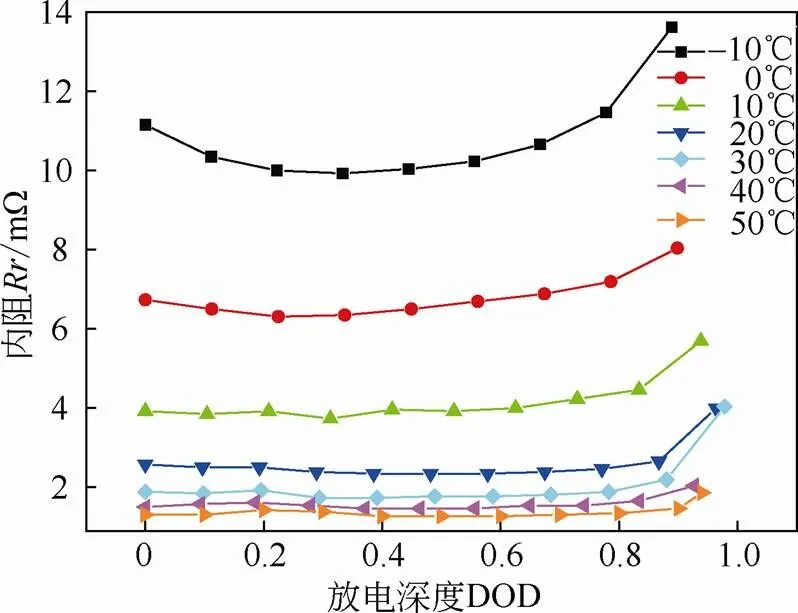
图2 不同温度下的内阻

由图2可以看出，在不同的环境温度下，内阻随温度的升高而整体降低，最低达到1.3 mΩ；在环境温度10～50 ℃时，内阻在10%～90%DOD范围内变化不大，在90%～100%DOD范围内逐渐增大；在-10～10 ℃时，内阻随着DOD先减小再增大。从测得数据整体来看，温度对内阻的影响比较显著，内阻的大小又直接影响电池的容量及充放电效率，所以对电池来说，控制合理的环境温度对其性能十分重要。

根据内阻值，对内阻随温度和放电深度的变化关系进行二元有理式拟合，得到关系曲面（图3）和关系式[式(1)]，相关系数0.99。

=(6.67511-0.08387×+1.81951×DOD

-10.19198×DOD2+11.4049×DOD3)/

(1+0.04027×+7.76235×10-4×2-2.43016×10-5×3+0.16896×

DOD0.18195×DOD2) （1）

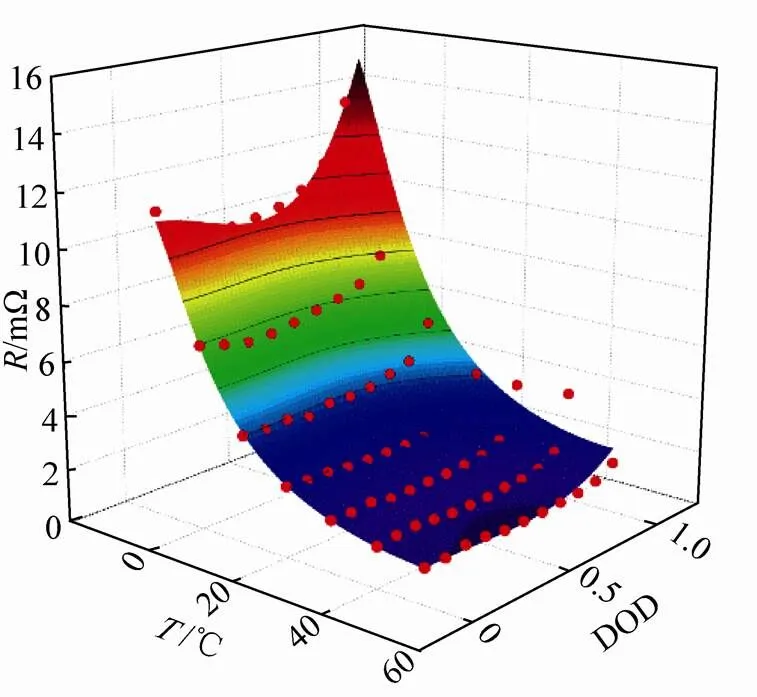
图3 内阻、温度和放电深度的拟合曲面

1.2.2 温升测试

为测量电池放电过程中的温升数据，在电池表面布置T型热电偶，记录电池在放电过程中的温度变化，使用绝热材料（绝热气凝胶）对电池表面进行双层包裹，放置在高低温防爆实验箱中，防爆箱温度控制在30 ℃，测量电池0.5 C放电倍率下的温度变化，如图4所示。测试前将电池在室温下以恒流恒压方式充电至4.2 V，截止电流0.1 C；静置2 h；放置在防爆箱中恒温至30 ℃；然后0.5 C放电至2.75 V。

1.2.3 温降测试

电池在放电温升测试中虽然进行了两层绝热包裹，仍然有部分热量通过对流换热和辐射换热散失到环境中去，根据CHEN[9]提出的将两者转化为折合对流换热系数简化计算。为了求出折合换热系数，需要对电池进行同一环境条件下的温降测试。电池放电结束后满足热平衡公式：

图4 温升实验测试图

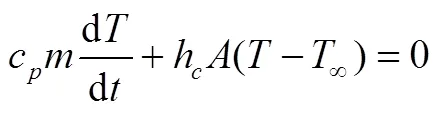
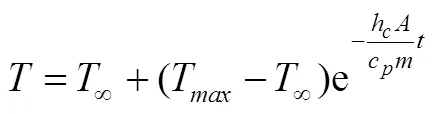
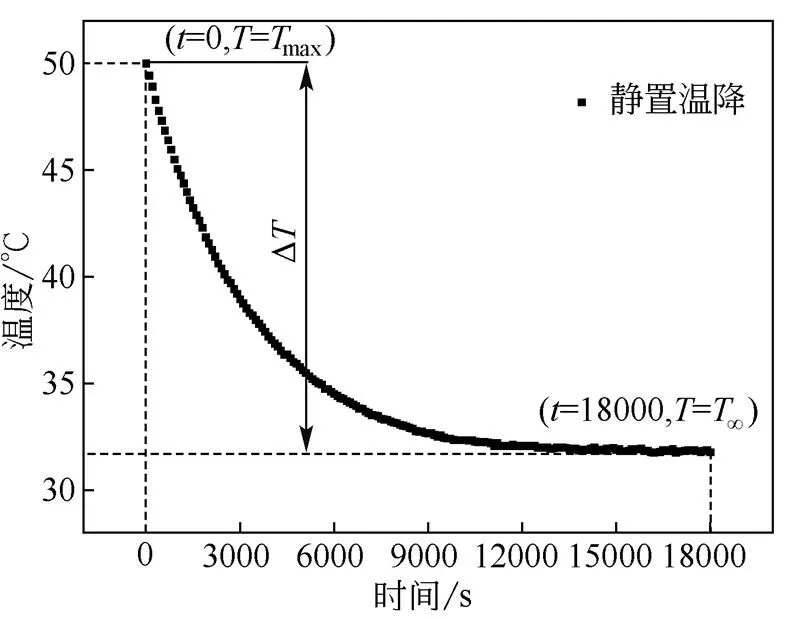
图5 静置温降变化图

2 热模型

2.1 电池生热模型

电池生热模型是基于Bernardi[2]生热基本理论公式，忽略内部离子浓度梯度引起的混合热和相变热，假设内部物质均匀发热，生热率公式[1]简化为式(4)

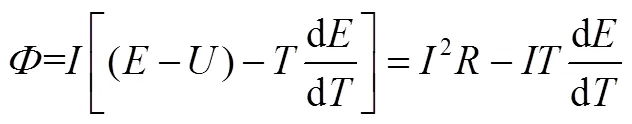
根据电池放电过程中的热平衡方程，电池放电过程中产生的热量一部分被自身吸收，另一部分通过对流传热和辐射传热散失到环境中，根据CHEN等[9]提出的可以将两种散热转化为对流换热计算，通过折合对流换热系数h体现，可以得到下列公式：

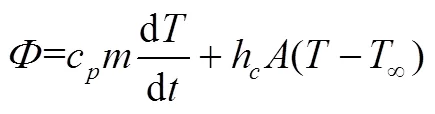
2.2 热物性参数

由于模型采用集中质量模型，所以忽略电池内部的各向热导率；根据OHDA等[10]通过实验测得的锂离子电池比热容随温度的变化关系，比热容随温度的变化不大，电池整体平均比热容c=1244 J/(kg·K)；电池在测试过程中的换热系数h=2.895 W/(m2·K)。

2.3 熵热系数

SATO等[11]通过对80 A·h软包锂离子电池实验得出，在小于26 A放电时电池可逆反应热大于内阻热，在大于26 A放电时可逆反应热小于内阻热；放电电流越大，内阻热占总热量的比例越大。根据电池生热模型[式(4)]可以看出，放电电流越大，内阻热在总生热量的比例越大，熵热占的比重相对越小，计算得到的熵热系数误差越大；然而由于放电电流太小则会造成温升变化不明显，测试误差增大。所以经多次实验，选取0.5 C倍率放电过程计算电池的熵热系数（d/d）。

通过0.5 C放电倍率绝热温升测试，测量电池在放电过程中的温度变化。根据式(5)计算得到0.5 C放电倍率下的生热率变化。

图6为0.5 C倍率下的生热率曲线，对其进行7次多项式拟合，得到该倍率下瞬态生热速率曲线。可以明显的看到，在～段，生热速率有明显的下降，在45%DOD附近生热速率达到最小，对应了放电中期的温度剧烈波动，放电末期～段生热率迅速增大。

图7为电池熵热系数随DOD的变化过程，正值代表可逆反应热为吸热过程，负值代表放热过程。可以看出，熵热系数随放电深度呈现一定的波动性变化，其中～、～、～是下降段，～、～是上升段；在～段，熵热系数为正值，说明在放电中期电池内部的可逆反应热为吸热反应，造成了电池在小倍率放电中期温度的下降；在放电末期～段，可以看出熵热系数急剧减小，反应热放热量迅速增大。电池熵热系数d/d的变化范围为-0.85～0.05 mV/K。

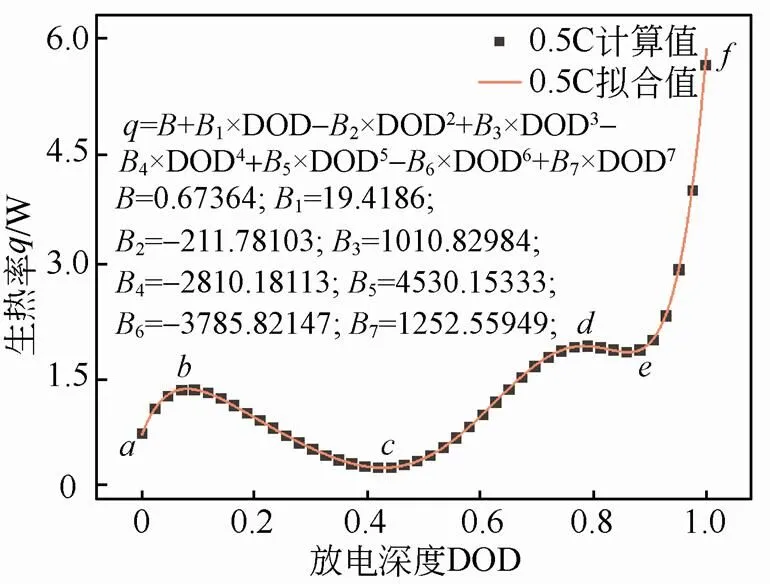
图6 0.5 C放电倍率下的瞬态生热曲线

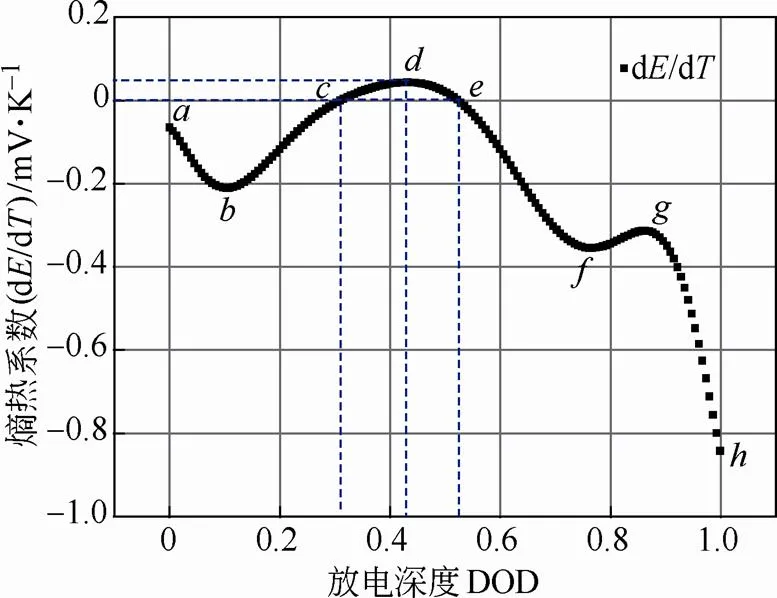
图7 熵热系数随DOD变化图

3 结果对比

基于以上电池集中质量生热模型[式(2)]，根据实验测试的内阻随温度和放电深度的变化关系[式(1)]，熵热系数随放电深度的变化关系（图7），进行不同放电倍率下电池温度仿真，并与不同放电倍率下的温度测试值进行对比。为保证电池上升的温度不至于过高，随着放电倍率的增大，测试时所设定的环境温度略有降低，具体如图8中所示。

图8为不同放电倍率下的电池温升曲线对比。可以看出，不同放电倍率下的电池温升模拟值与实验值相吻合，电池的初始温度和最终温度相一致；在小倍率放电过程中，可以很好地模拟出电池在放电过程中的非线性变化过程。随着放电倍率的增大，电池温度的波动性减小，在3 C放电时，温升曲线与放电深度趋于线性关系。

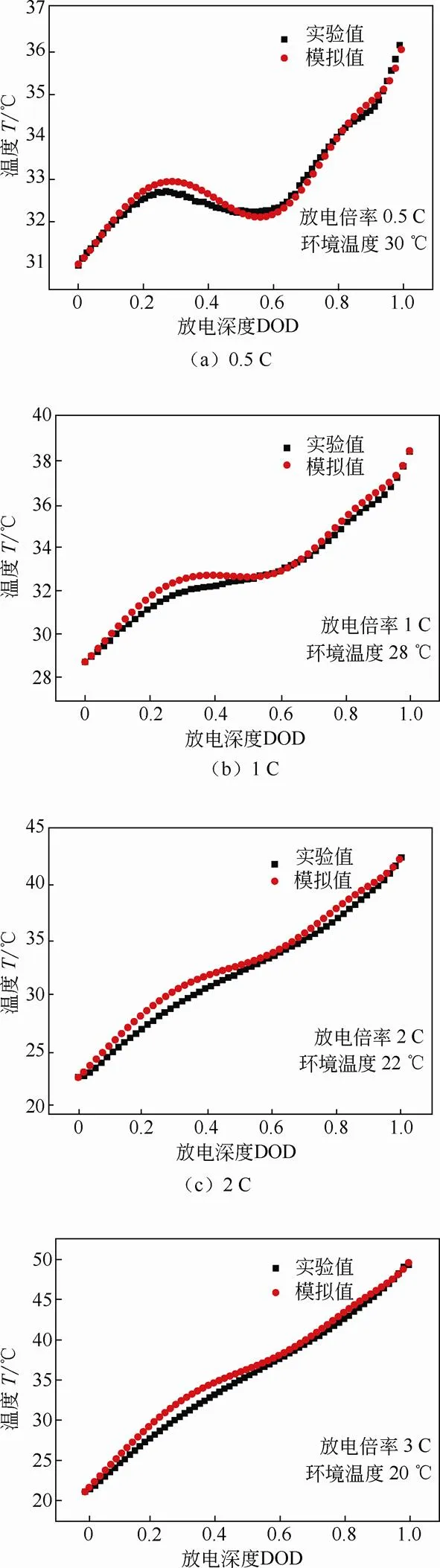
（d）3 C

通过测试不同放电倍率下的温度，根据式(4)计算出不同放电倍率下的生热率，结果与模拟值进行对比，见图9。通过图9可以看出，该模型可以很好地模拟电池生热率变化，尤其是在0.5 C、1 C放电倍率条件下，电池生热率模拟值与计算值的变化曲线基本一致，可以模拟电池在放电过程中的温度变化过程，为电池温变的过程分析及电池热管理的过程控制提供指导。

将不同放电倍率下生热率的模拟平均值与计算值平均值进行对比，如图10所示，可以看出电池平均生热率的模拟值略大于计算值，最大误差出现在1 C放电时，模拟值仅略高于计算值约5.4%，模拟结果精确度较高，能够模拟不同放电倍率下锂离子电池的发热量。

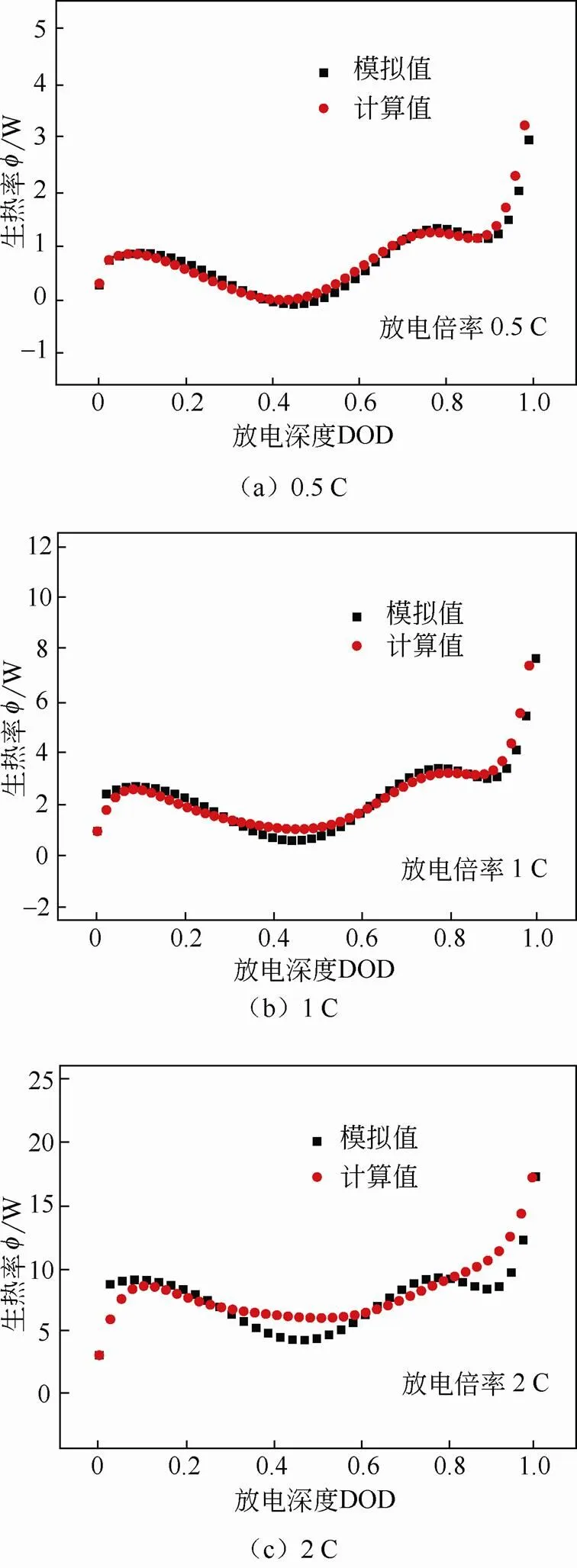
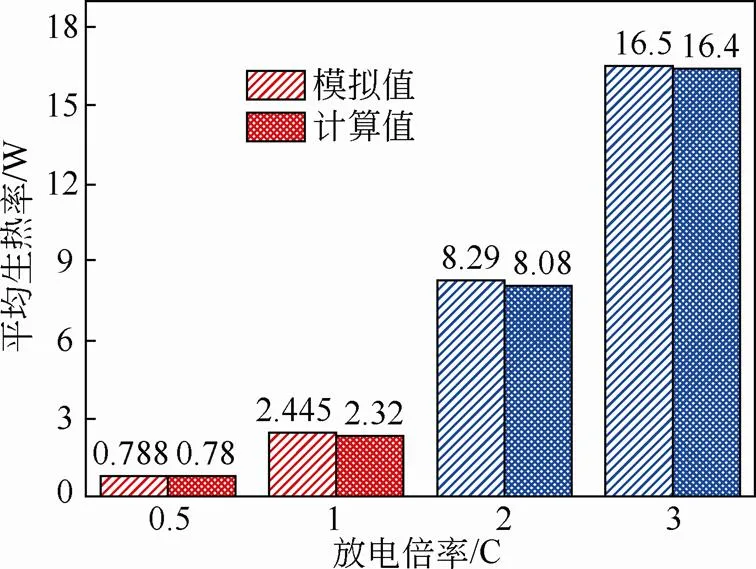
图10 不同放电倍率下的生热率平均值对比

4 结 论

本文依据电池产热基本模型，根据0.5 C放电倍率下的温升实验计算出电池瞬态熵热系数，建立生热率随放电深度不断变化的瞬态生热模型，基于该模型进行不同放电倍率的温度仿真模拟，并与实验进行对比验证，结果表明。

（1）该模型可以很好地模拟电池在不同放电倍率下的温度变化以及生热速率的变化，展现电池温度在小倍率放电过程中的非线性变化特征。

（2）电池在放电过程中熵热的波动影响电池温度的变化，在小倍率放电中期，熵热出现吸热反应，造成电池放电过程中温度的降低，电池熵热系数的变化范围约为-0.85～0.05 mV/K。

[1] 刘霏霏, 兰凤崇, 陈吉清. 基于动态内热源特性的车用锂离子动力电池温度场仿真及实验[J]. 机械工程学报, 2016(8): 141-151.

LIU Feifei, LAN Fengchong, CHEN Jiqing. Simulation and experiment on temperature field of lithium-ion power battery for vehicle based on characteristic of dynamic heat source[J]. Journal of Mechanical Engineering, 2016(8): 141-151.

[2] 李腾, 林成涛, 陈全世. 锂离子电池热模型研究进展[J]. 电源技术, 2009(10): 927-932.

LI Teng, LIN Chengtao, CHEN Quanshi. Research development on lithium-ion battery thermal model[J]. Chinese Journal of Power Sources, 2009(10): 927-932.

[3] BERNARDI D, PAWLIKOWSKI E, NEWMAN J. A general energy balance for battery systems[J]. J. Electrochemical Society, 1985, 132(1): 5-12.

[4] 云凤玲, 卢世刚. 基于高镍三元材料锂离子动力电池在循环前后的热特性分析[J]. 稀有金属, 2014, 38(6): 283-292.

YUN Fengling, LU Shigang. Thermal characteristic analysis of lithium ion power battery based on high nickel ternary material before and after cycle[J]. Chinese Journal of Rare Metals., 2014, 38(6): 283-292.

[5] 匡勇, 刘霞, 钱振, 等. 锂离子电池产热特性理论模型研究进展[J]. 储能科学与技术, 2015, 4(6): 599-608.

KUANG Yong, LIU Xia, QIAN Zhen, et al. Review on heat generation theory model of lithium-ion battery[J]. Energy Storage Science and Technology, 2015, 4(6): 599-608.

[6] 李斌, 常国峰, 林春景, 等. 车用动力锂电池产热机理研究现状[J]. 电源技术, 2014, 38(2): 378-381.

LI Bin, CHANG Guofeng, LIN Chunjing, et al. Research on heat generate mechanism of Li-ion batteries for electric vehicles[J]. Chinese Journal of Power Sources, 2014, 38(2): 378-381.

[7] 吴彬. 锂离子动力电池热设计方法研究[D]. 北京: 清华大学, 2015.

WU Bin. Thermal design methodology for traction lithium-ion batteries[D]. Beijing: Tsinghua University, 2015.

[8] 郭宏榆, 姜久春, 王吉宋, 等. 功率型锂离子动力电池的内阻特性[J]. 北京交通大学学报, 2011, 35(5): 119-123.

GUO Hongyu, JIANG Jiuchun, WANG Jisong, et al. Characteristic on internal resistance of lithium-ion power battery[J]. Journal of Bejing Jiaotong University, 2011, 35(5): 119-123.

[9] CHEN S C, WAN C, WANG Y. Thermal analysis of lithium-ion batteries[J]. Journal of Power Sources, 2005, 140(1): 111-124.

[10] ONDA K, OHSHIMA T, NAKAYAMA M, et al. Thermal behavior of small lithium-ion battery during rapid charge and discharge cycles[J]. Journal of Power Sources, 2006, 158(1): 535-542.

[11] SATO N. Thermal behavior analysis of lithium-ion batteries for electric and hybrid vehicles[J]. Journal of Power Sources, 2001, 99(1): 70-77.

[12] 陈燕虹, 吴伟静, 刘宏伟, 等. 纯电动汽车电池箱的热特性[J]. 吉林大学学报(工学版), 2014, 44(4): 925-932.

CHEN Yanhong, WU Weijing, LIU Hongwei, et al. Thermal characteristics of battery for pure electric vehicles[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(4): 925-932.

Simulation and verification of lithium-ion battery temperature changing process

MA Long, WEN Hua

(School of Mechanical & Electrical Engineering, Nanchang University, Nanchang 330031, Jiangxi, China)

To investigate the temperature-variation of the soft package lithium-ion battery during discharge, based on the basic heat generation model, through internal resistance test and temperature rise experiment under 0.5 C discharge, the transient heat rate curve is calculated and entropy coefficient is obtained. A transient thermal model can be established and the heating rate varies with the depth of discharge changing. The temperature variation was simulated by using this model and compared with the experiment. It shows that the simulation results are consistent with the experiment. This model can simulate the battery temperature change process under different discharge ratio very well, which has guiding mean for the battery temperature variation analysis and the thermal management.

lithium-ion battery; thermal characteristic; entropy coefficient; temperature variation

10.12028/j.issn.2095-4239.2018.0003

TM 911

A

2095-4239（2018）04-0712-06

2018-01-12；

2018-01-31。

国家自然科学基金项目（51762034）。

马龙（1988—），男，硕士研究生，研究方向为锂离子电池热分析，E-mail：ml@email.ncu.edu.cn；

文华，副教授，研究方向为电动汽车电池热管理，E-mail：wenhua25@ncu.edu.cn。