动力吸振器刚度和阻尼偏差对浮置板轨道低频振动控制的影响

王建伟

(北京城建设计发展集团股份有限公司,北京 100037)

本文基于扩展定点理论与车辆-轨道耦合动力学模型[14]，对附加动力吸振器的钢弹簧浮置板轨道的关键设计参数作进一步分析，着重探讨在动力吸振器偏离最优刚度与阻尼情况下浮置板的低振动控制效果，为动力吸振器在浮置板轨道低频振动控制中的实际运用提供一定的参考。

1 动力吸振器设计及低频振动控制评价方法

1.1 动力吸振器设计参数

基于单自由度系统，文献[12-13]对扩展定点理论进行了详细介绍。轨道板是具有多阶模态的连续系统，可基于模态分析技术，利用模态向量的正交性将轨道连续体系统离散为多个单自由度集成的非耦合模型，然后使用单自由度系统制振设计方法进行设计。附加动力吸振器的轨道板示意见图1。

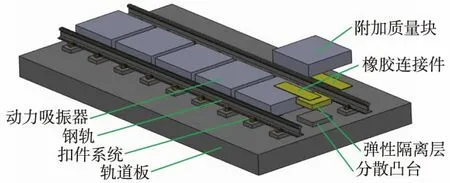
图1 附加动力吸振器的轨道板示意

根据多自由度等价质量识别法可知，轨道板第i阶模态的等价质量Mi与刚度Ki可以通过以下公式[7]计算

(1)

(2)

式中，Ei为轨道板对应第i阶模态的总动能；ωi为轨道板第i阶的固有频率。

根据文献[11-12]可以得到控制浮置板轨道第i阶模态的动力吸振器的最优设计参数

mi=μiMi

(3)

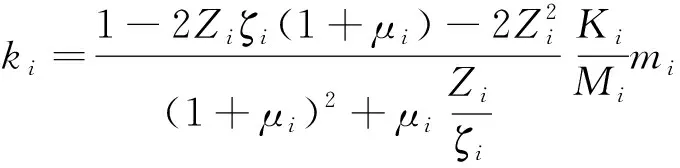
(4)

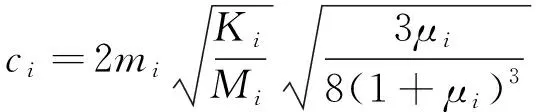
(5)

式(3)～式(5)中，μi为质量比；mi为动力吸振器质量；ki为动力吸振器最优刚度；ci为动力吸振器最优阻尼；Zi为浮置板轨道第i阶模态等效阻尼比；ζi为动力吸振器第i阶模态等效阻尼比。

由式(3)～式(5)可知，只要选定质量比μi，便可求出动力吸振器质量与最优阻尼。至于动力吸振器的最优刚度，可以先求出Zi=0时动力吸振器的最优刚度，然后根据最优同调的原则适当降低刚度值加以调试确定。

1.2 浮置板轨道模态分析

本文按照实验室浮置板轨道尺寸建立有限元模型，其中浮置板长9.06 m，宽3.15 m，厚0.495 m，钢轨之间无凸台。钢轨采用梁单元模拟，钢轨两端施加简支约束；轨道板采用实体单元模拟，纵向两个端面施加对称约束来模拟轨道板之间剪力铰的作用；扣件系统和钢弹簧隔振器均采用弹簧-阻尼单元模拟，其中钢弹簧隔振器底端施加固定约束[15]。浮置板轨道主要结构参数见表1。

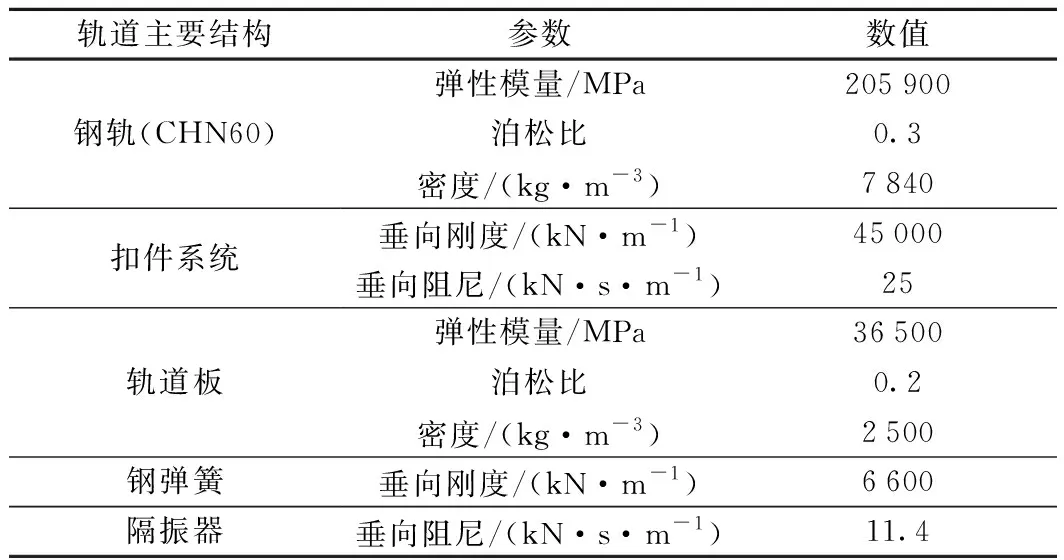
表1 浮置板轨道主要结构参数

为对浮置板轨道有限元模型进行修正与验证，保证计算参数的准确性与可靠性，本文对实验室浮置板轨道进行现场模态测试。测试中，采用德国M+P公司的VibPilot动态测试与分析软件作为数据采集系统和分析软件，通过对轨道板不同位置进行锤击，采集轨道板振动响应，并采用m+p SmartOffice V4.4模态分析软件进行分析，从而获得浮置板轨道前4阶固有频率与相应的模态振型。将模态测试的结果与仿真结果进行对比，不断修正有限元模型的计算参数，从而保证浮置板轨道有限元模型的准确性与可靠性。

浮置板轨道模态测试结果与仿真结果的对比见表2，前4阶模态振型如图2、图3所示。

由表2可知，浮置板轨道仿真结果与模态测试结果偏差在±3%以内；由图2与图3可知，浮置板轨道第1阶模态振型以垂向平动为主，第2阶与第3阶以刚体转动为主，第4阶以垂弯为主，且仿真分析的模态振型与模态测试结果保持了一致性，从而验证了浮置板轨道有限元模型的准确性与可靠性，为浮置板轨道动力吸振器的设计准备了条件。

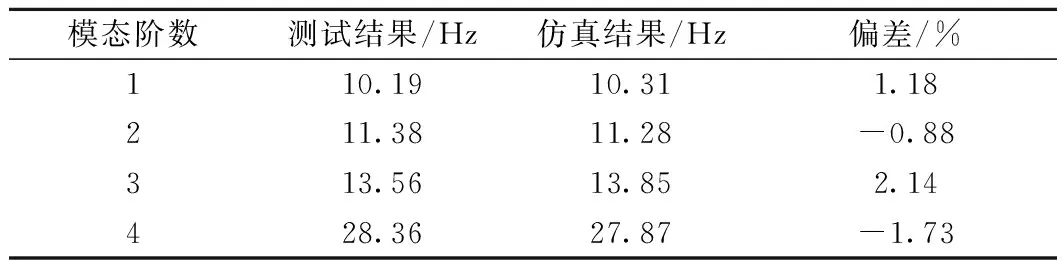
表2 浮置板轨道模态测试结果与仿真结果对比

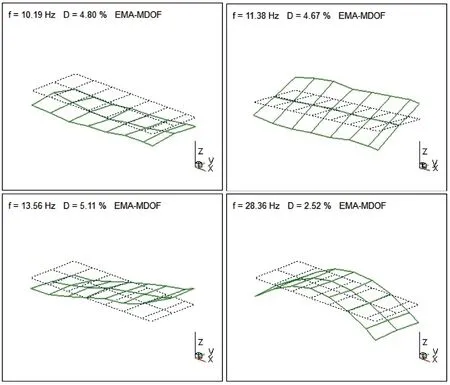
图2 浮置板轨道模态测试结果

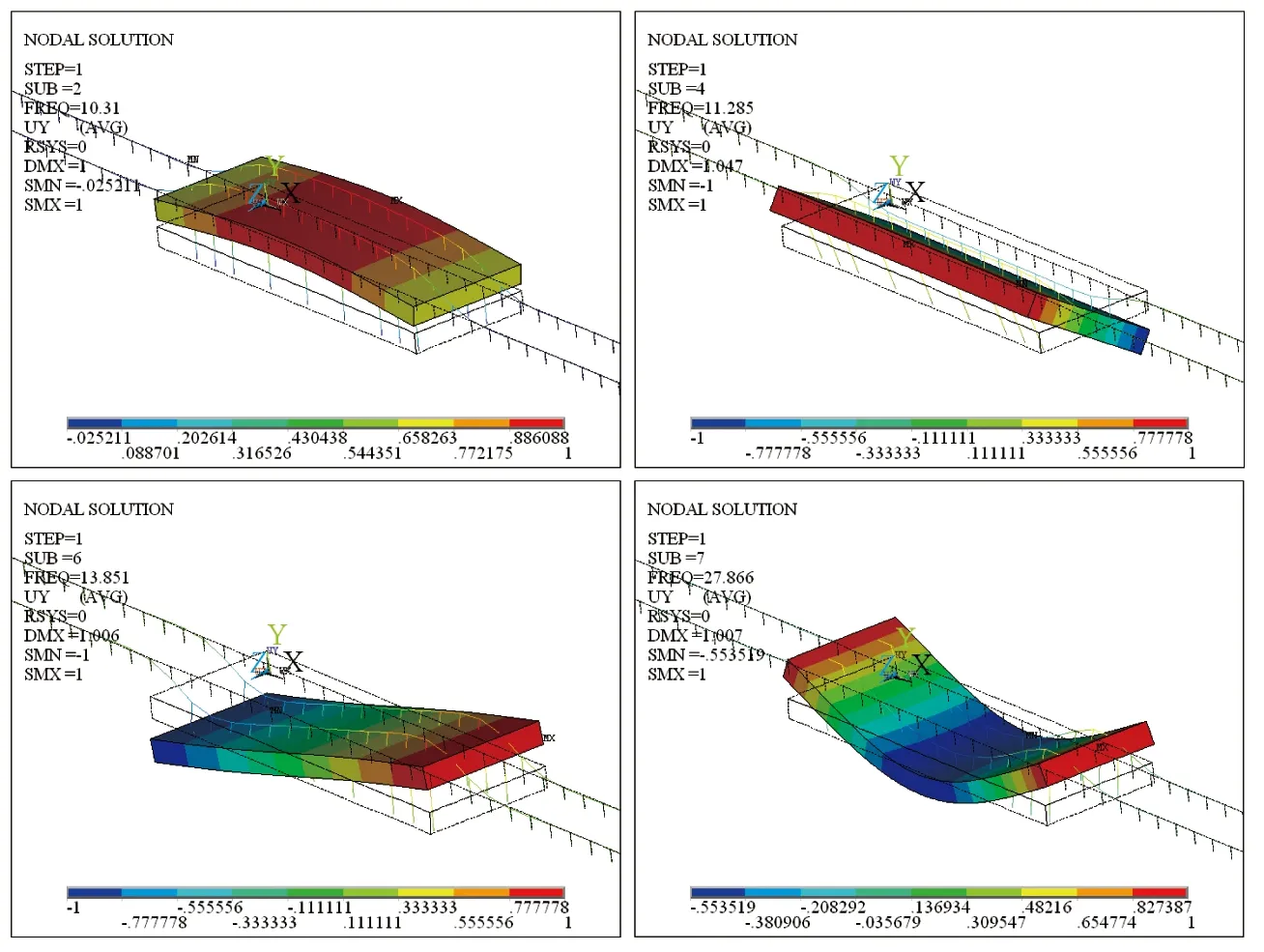
图3 浮置板轨道模态仿真结果

1.3 附加动力吸振器的浮置板轨道有限元模型

由于浮置板轨道低频域振动放大的现象主要发生在第1阶固有频率处，故本文主要控制浮置板轨道第1阶模态，抑制浮置板轨道垂向振动。根据式(1)、式(2)可得到轨道板第1阶模态的等价质量和刚度分别为33 400 kg和149 970 kN/m。选定质量比为0.3，由式(3)～式(5)可得到抑制浮置板轨道第1阶模态的动力吸振器的最优参数。考虑到浮置板轨道第1阶模态主要以垂向振动为主，集中质量块与离散质量块的控制效果相同，本文将集中质量块离散为6块，平均分布在浮置板轨道纵向中心线上，每个质量块的质量、刚度与阻尼为原参数的1/6。表3列出了单个动力吸振器的最优参数，图4给出了附加动力吸振器的浮置板轨道有限元模型，其中动力吸振器附加质量块采用质量单元模拟，弹性连接件采用弹簧-阻尼单元模拟。

表3 动力吸振器的最优参数

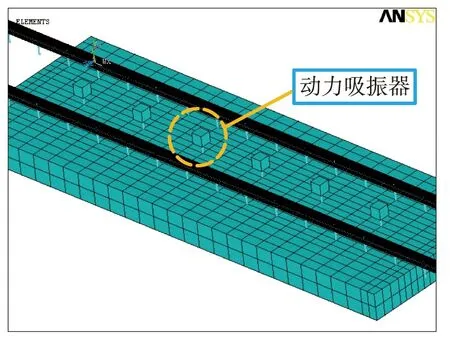
图4 附加动力吸振器的浮置板轨道有限元模型

1.4 低频振动控制效果评价方法

《浮置板轨道技术规范》(CJJ/T191—2012)规定了浮置板轨道减振效果评价方法。浮置板轨道与整体道床比较时分频振级均方根的差值ΔLa宜按以下公式计算

(6)

式中VLq(i)——选择没有采用浮置板轨道的地段为参考系，其轨旁测点铅垂向振动加速度在1/3倍频程第i个中心频率的分频振级，dB；

VLh(i)——采用浮置板轨道的地段，其轨旁测点铅垂向振动加速度在1/3倍频程第i个中心频率的分频振级，dB。

附加动力吸振器的浮置板轨道相对于普通整体式道床的减振量ΔLa2与无动力吸振器的浮置板轨道相对于普通整体式道床的ΔLa1的差值如下

(7)

(8)

ΔLa2-1=ΔLa2-ΔLa1=

(9)

ΔLa2-1为无动力吸振器的浮置板轨道与附加动力吸振器的浮置板轨道的分频振级均方根的差值，可作为动力吸振器综合振动控制效果的评价指标。

2 计算方案的确定

由表3可知，动力吸振器的最优设计参数表现为“小刚度，大阻尼”的特点，表明动力吸振器在抑制轨道板低频振动峰值的同时，自身振动加剧，将振动能量消耗在弹性连接元件中，从而达到降低浮置板低频振动的效果。但制作弹性连接件同时满足小刚度、大阻尼是比较困难的，又由于材料制作工艺的限制，动力吸振器参数与设计参数难免存在偏差，故有必要分析动力吸振器参数偏差对浮置板轨道低频振动控制效果的影响。表4列出了具体的计算方案，其中工况0为动力吸振器最优参数工况，工况1～工况3为动力吸振器阻尼偏差工况，工况4～工况8为动力吸振器刚度偏差工况。

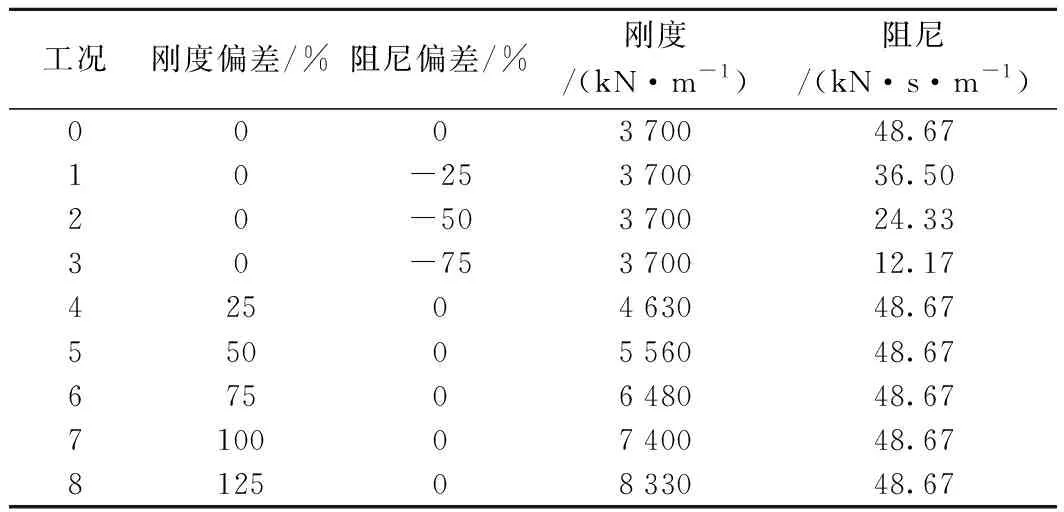
表4 动力吸振器参数偏差计算方案

3 附加动力吸振器的浮置板轨道谐响应分析

针对附加动力吸振器的浮置板轨道有限元模型，按照表4所列计算方案，对附加动力吸振器的浮置板轨道进行谐响应分析，其中简谐荷载施加在钢轨上，大小为15 kN，分析频率范围0～30 Hz。

图5和图6分别给出了阻尼偏差与刚度偏差工况下浮置板轨道的板中位置的幅频响应曲线。

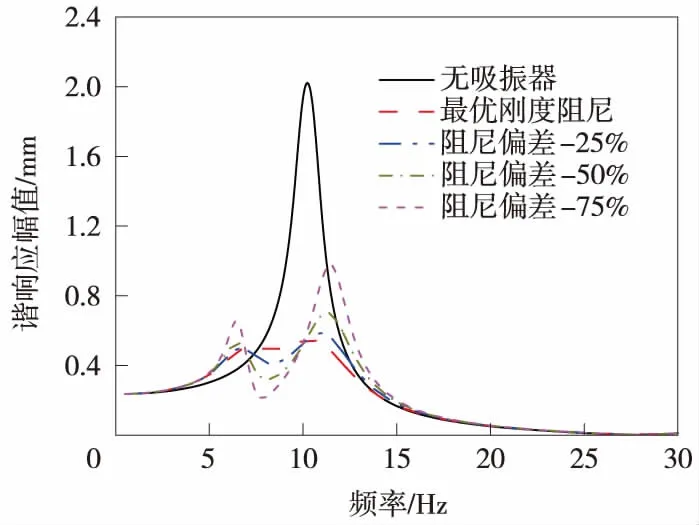
图5 阻尼偏差工况下浮置板轨道的幅频响应曲线

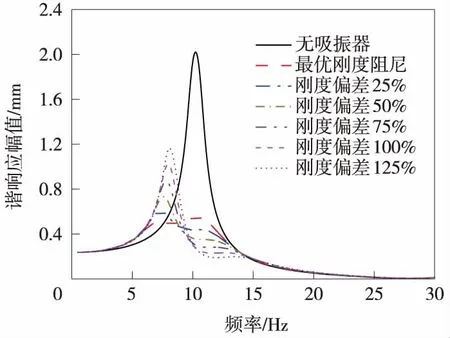
图6 刚度偏差工况下浮置板轨道的幅频响应曲线

由图5可知，无动力吸振器时，浮置板轨道振动位移在固有频率处存在较大的峰值，采用吸振器后，该峰值得到有效抑制，当吸振器阻尼偏离最优值时，浮置板轨道振动位移在固有频率两侧出现较为明显的峰值，其大于最优阻尼工况下的峰值但均小于无吸振器时的峰值，且随着阻尼偏离增大，即阻尼参数减小，两侧峰值增大，吸振器的振动控制效果下降。由图6可知，当动力吸振器刚度偏离最优值125%以内时，浮置板轨道振动位移在固有频率左侧出现较为明显的峰值，其频率在7～8 Hz，且随着刚度偏差增大，即刚度参数增大，左侧峰值增大，在该频率段，动力吸振器的振动控制效果下降。

4 列车动荷载下附加动力吸振器的浮置板轨道低频振动控制效果分析

本文基于车辆-轨道耦合动力学理论[14]，建立地铁车辆-浮置板轨道耦合动力学模型，如图7所示，计算得到轮轨相互作用力，并将其导入附加动力吸振器的浮置板轨道有限元模型中进行动力学计算。其中，地铁车辆运行速度取80 km/h，轨道不平顺采用波长范围为1～30 m的美国五级轨道谱。

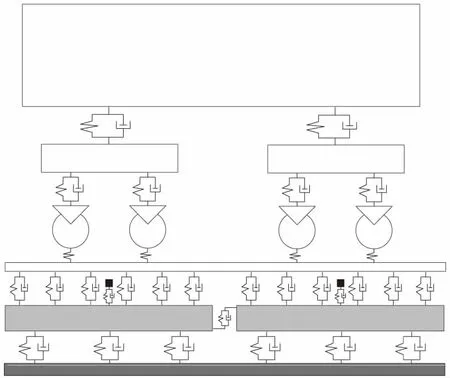
图7 地铁车辆-浮置板轨道垂向耦合动力学模型

图8、图9分别给出了动力吸振器阻尼偏差和刚度偏差工况下浮置板轨道板中位置的1/3倍频程下的振级。

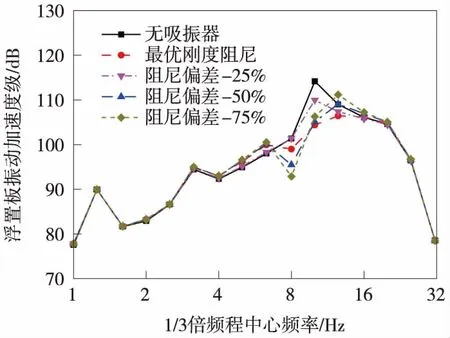
图8 阻尼偏差工况下浮置板轨道的振级

图9 刚度偏差工况下浮置板轨道的振级

由图8可知，在列车动荷载作用下，浮置板轨道在中心频率10 Hz处振级最大，应用最优参数下的动力吸振器后，浮置板轨道在中心频率10 Hz处的振级明显降低，同时在附近频段浮置板轨道的振级与无吸振器时相差不大，而在阻尼偏离最优值时，浮置板轨道在中心频率10 Hz两侧频段出现振级放大的现象。由图9可知，在刚度偏离最优值125%以内时，浮置板轨道的振级在4～8 Hz有放大现象，但在中心频率10 Hz处，浮置板振级比最优参数工况下小。

由式(9)可计算得到表3所列工况下无动力吸振器的浮置板轨道与附加动力吸振器的浮置板轨道分频振级均方根的差值，即动力吸振器在32 Hz以内的综合振动控制效果，如图10所示。

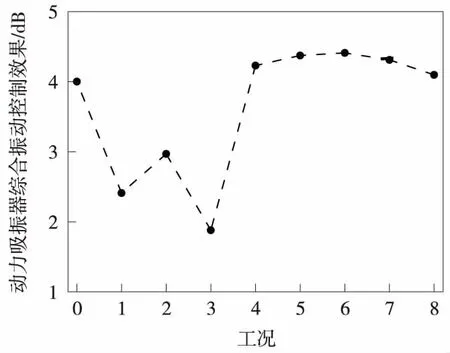
图10 不同工况下浮置板轨道综合振动控制效果

由图10可知，采用最优参数下的动力吸振器时，吸振器在32 Hz以内的综合振动控制效果达到4 dB左右；当阻尼偏离最优值时，吸振器综合振动效果降低，在阻尼偏离最优值-75%工况下，综合振动控制效果为1.9 dB，比最优参数工况降低了2.1 dB；当刚度偏离最优值时，吸振器的综合振动控制效果比最优参数工况有所增加，在刚度偏离最优值75%工况下，综合振动控制效果为4.4 dB，增加了0.4 dB。

5 结论

本文基于扩展定点理论，并结合车辆-轨道耦合动力学模型，对浮置板轨道动力吸振器的关键设计参数开展研究，着重分析了动力吸振器刚度与阻尼参数偏离其最优值时对浮置板轨道的低频振动控制效果的影响。通过仿真分析，得到以下结论。

(1)当动力吸振器阻尼偏离最优值时，浮置板轨道振动位移响应在固有频率10 Hz两侧出现明显的峰值，该峰值介于最优参数工况和无吸振器工况下的峰值之间，且该峰值随阻尼参数偏差的增大而增大；当动力吸振器刚度偏离最优值125%以内时，浮置板轨道振动位移响应在固有频率10 Hz左侧出现较为明显的峰值，且随着刚度偏差增大而增大，动力吸振器对浮置板轨道在该频段的振动控制效果降低。

(2)当动力吸振器的刚度与阻尼为最优参数时，吸振器能够有效地降低浮置板轨道在中心频率10 Hz处的振级，同时不会明显引起10 Hz附近频段振级的放大，而动力吸振器刚度与阻尼偏离最优值时将会引起10 Hz附近频段振级的放大。

(3)由动力吸振器综合振动控制效果分析可知，当阻尼偏离最优值时，吸振器对浮置板轨道32 Hz以内的综合振动控制效果降低，在阻尼偏离-75%工况时，综合振动控制效果比最优参数工况降低2 dB，而刚度偏离最优刚度时，低频振动控制效果有所增加，在偏离75%工况下，振动控制效果增加0.5 dB。

(4)动力吸振器刚度与阻尼参数的偏差对浮置板轨道的振动控制效果影响较大，在其实际应用过程中，应结合材料的配方与工艺，以求达到动力吸振器最佳的控制效果。

[1] 姚京川，杨宜谦，王澜.浮置板式轨道结构隔振效果分析[J].振动与冲击，2005，24(6)：108-113.

[2] 张生延.浮置板与整体道床轨道车轨振动特性对比分析[J].铁道标准设计，2016，60(11)：10-13.

[3] Crockett A R， Pyke J R. Viaduct design for minimization of direct and structure radiated train noise[J]. Journal of Sound and Vibration， 2000，231(3):883-897.

[4] Lombaert G， Degrande G， Vanhauwere B， et al. The control of ground-borne vibration from railway traffic by means of continuous floating slabs[J]. Journal of Sound and Vibration， 2006，297(3-5):946-961.

[5] 李俊岭.地铁钢弹簧浮置板轨道对环境振动的影响分析[D].成都：西南交通大学，2009.

[6] 刘卫丰，刘维宁，马蒙，等.地铁列车运行引起的振动对精密仪器的影响研究[J].振动工程学报，2012，25(2)：130-137.

[7] 丁德云.地铁列车振动环境响应低频特征的分析与研究[D].北京：北京交通大学，2010.

[8] Zhu Shengyang， Yang Jizhong， Yan Hua， et al. Low-frequency vibration control of floating slab tracks using dynamic vibration absorbers[J]. Vehicle System Dynamics， 2015，53(9)：1296-1314.

[9] 杨吉忠，张雷，蔡成标，等.低频域多模态制振轨道板设计[J].西南交通大学学报，2015，50(6)：1082-1087.

[10] 杨吉忠，颜华，蔡成标.城市轨道交通低频减振轨道结构研究[J].铁道学报，2015，37(9)：90-95.

[11] 张龙庆，朱胜阳，蔡成标，等.动力吸振器在浮置板轨道低频振动控制中的应用[J].工程力学，2016，33(9)：212-219.

[12] 背户一登.动力吸振器及其应用[M].任明章，译.北京：机械工业出版社，2013.

[13] 背户一登.结构振动控制[M].马立新，李孜，译.北京：机械工业出版社，2011.

[14] 翟婉明.车辆-轨道耦合动力学[M].北京：科学出版社，2007.

[15] 丁德云，刘维宁，张宝才，等.浮置板轨道的模态分析[J].铁道学报，2008，30(3)：61-64.