基于SPA-MLR方法的土壤含水量光谱预测模型研究

贾学勤，冯美臣，杨武德，王 超，孙 慧，武改红，张 松

(山西农业大学农学院, 山西 太谷 030801)

土壤水分对植物的生长发育具有重要的影响，与植物和外界环境间的物质和能量交换密切相关，也是植物生长状况监测的重要指标[1],因此土壤含水量的快速准确测定对于农业生产具有重要意义。传统的测定土壤含水量的方法主要有烘干法、中子仪法以及时间域反射仪法(TDR)等，但耗时费力，且测定范围小，难以满足现代农业对大面积土壤含水量准确及时测量的需求[2]。

高光谱遥感监测具有快速、准确、无破坏的特点，在监测土壤含水量方面具有重要作用。随着高光谱遥感技术的快速发展，光谱分辨率不断提高，光谱信息极大丰富的同时也增大了背景和噪音的影响，进而增加准确提取特征光谱信息的难度，影响监测模型的精度[3]。研究发现光谱数据变换在消除背景和噪音干扰，降低内外部因子的影响，放大光谱吸收特征方面具有较好的效果，有利于光谱信息的挖掘和提取，进而提高监测模型的精度和稳定性[4,5]。Kemper等[6]对土壤原始光谱反射率进行一阶微分处理，提高了土壤重金属、粘粒含量等的监测精度。何挺等[7]研究表明反射率对数一阶微分变换，提高了土壤光谱与含水量的相关性。伊叶彪等[8]通过土壤光谱去包络线后进行一阶微分，预测含水量R2达到了0.855。谢伯承等[9]利用反射率倒数的对数(A)、A值的一阶微分和相对反射率反演土壤含水量，得出A的一阶微分反演效果最佳，且土壤含水量与光谱反射率呈明显非线性关系。姚艳敏等[10]对土壤光谱反射率进行光谱变换，预测黑土土壤含水量，结果表明反射率进行对数一阶微分变换后建立的模型最好，R2达到了0.931。张俊华等[11]研究得出高光谱预测龟裂碱土土壤含水量最优模型为使用反射率一阶微分的幂函数模型，R2高达0.9447。目前，光谱变换已广泛应用于光谱数据处理中，但是不同研究中各种变换方法效果不一。本文以此为切入点，在前人研究的基础上，首先对原始光谱进行11种常规变换，然后选择连续投影算法(SPA)选择特征波段，结合多元线性回归(MLR)建立土壤含水量光谱监测模型。旨在利用SPA-MLR实现不同光谱变换方法监测土壤含水量，并分析比较不同变换处理后各SPA-MLR回归模型的监测精度，进而选择出土壤含水量高光谱监测的最佳模型。

1 材料与方法

1.1 土壤样品采集与处理

本试验以山西省晋中市太谷县山西农业大学试验站的麦田土壤为研究对象，土壤质地为黄土母质发育而成的石灰性褐土，取表层土壤(0～20cm)为试验样品。土壤样品自然风干后剔除杂质，再研磨过2mm孔径筛后混匀。称取72份，每份100g，放于金属盒中，编号为1～72，然后进行土壤含水量调配，具体方法如下：在36h内，每隔0.5h取一份称量好的土样，向土壤中缓慢注水，使土壤达到饱和状态，注水后室温下使其自然蒸发。待最后一份土样注水完成、表面自由水消失后对所有土样进行光谱和含水量测定，从而得到72份不同含水量的土壤样本。其中土壤含水量用烘干法测得。

1.2 土壤光谱采集及预处理

本试验采用美国ASD公司的Field Spec Pro FR 型便携式光谱仪测定土壤光谱，波段范围为350～2500nm，在350～1000nm区间采样间隔为1.4nm，在1000～2500nm区间采样间隔为2nm。土壤光谱测定在暗室内进行，光源为50W卤素灯。光谱测量时光照方向与垂直方位夹角15°，光源距土壤表层40cm，采用10°视场角 ，探头位于土壤表面上方20cm处。光谱采集前进行标准白板校正，光谱采集时水平转动样品5次，每次转动60°，每个方向采集10条光谱曲线，共获得60个光谱数据，剔除异常值后将采集的光谱数据平均作为该土样反射率光谱。为消除噪声影响，本研究采用Savitzky-Golay3点平滑对光谱进行平滑去噪处理。由于350～400nm,2450～2500nm噪声影响较大，本研究选择400～2450nm波段范围进行研究。

1.3 光谱变换算法

本文在前人研究基础上选取11种典型的数学变换算法对光谱数据进行变换处理，如表1所示。

1.4 高光谱模型建立及模型评价

连续投影算法(SPA)可以有效降低光谱数据共线性，与偏最小二乘法(PLS)相比，可以最大程度地降低信息重叠度，有效地降低光谱模型复杂度[12]。且可以简化校正模型，缩短校正时间，已经越来越多地应用于特征波段的选取[13]。此外，还可以改善多元线性回归模型(MLR)的建模条件。SPA-MLR回归模型可以减小模型拟合复杂度，加快运算速度[14]。因此本研究选用SPA提取特征波段，结合MLR建立土壤含水量高光谱预测模型。

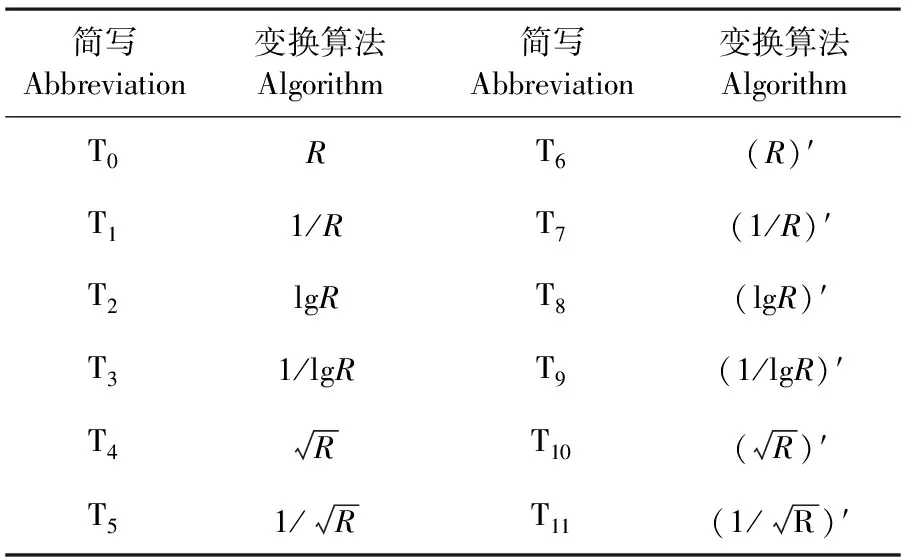
表1 11种光谱数据变换算法信息

注：R为波段λ(nm)处的反射率值。

Note:Ris the spectral reflectance value at the wavelengths ofλ(nm).

为确保土壤含水量模型稳定性和精度，将得到的土壤含水量样本(72个)随机分为两部分，选择48个样本用于构建模型，剩余24个样本用于模型验证。本研究采用相对预测偏差(RPD)，决定系数(R2)以及均方根误差(RMSE)作为模型预测精度的评价标准。其中，R2越接近于1，RMSE越小，表明模型具有高的预测精度和稳定性。当RPD大于2时，模型预测效果准确；当RPD大于1.4且小于2，模型预测效果一般可以粗略估计；当RPD小于1.4，模型无法进行准确预测[15]。

1.5 数据分析

本研究使用ViewSpec Pro光谱分析软件进行预处理，Excel 2007和Unscramb 10.3软件进行光谱、变换处理，Matlab 7.0和SPSS软件进行特征波段提取以及模型建立，Origin 8软件制图。

2 结果与分析

2.1 不同含水量土壤光谱特征

图1为不同含水量土壤光谱反射率曲线图，由图可以看出在400～2450nm范围内，随着土壤含水量增加光谱反射率不断降低。在可见光波段，光谱反射率随着土壤含水量的变化幅度明显小于近红外波段。在可见光-近红外波段(380～780nm)，随着波长增加反射率有升高的趋势，但是升高斜率不同；在1400nm、1900nm附近有两个明显的水分吸收谷。

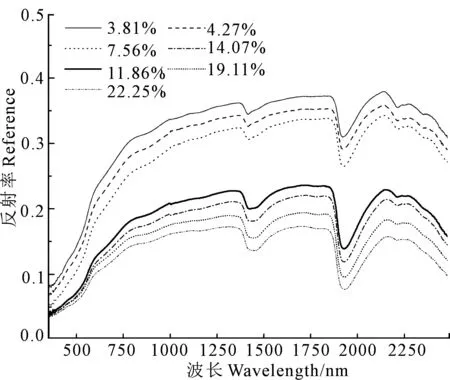
图1 不同含水量土壤的反射率曲线Fig.1 Spectral curves under of different soil moisture content

2.2 基于SPA方法和不同光谱变化方法提取的敏感波段

表2为光谱变换处理后基于SPA提取的土壤含水量最优波段个数和具体波段。由表2可知，最优波段个数都为3～5个，但是使用不同变换算法处理后光谱最优波段个数有一定差异，微分处理增加了最优波段个数。对不同变换算法处理后提取的光谱特征波段进行分析可知，提取的土壤含水量特征波段分布比较分散，特征波段在近红外、短波红外区域都有分布。不同变换算法处理后的特征波段有一定差异。

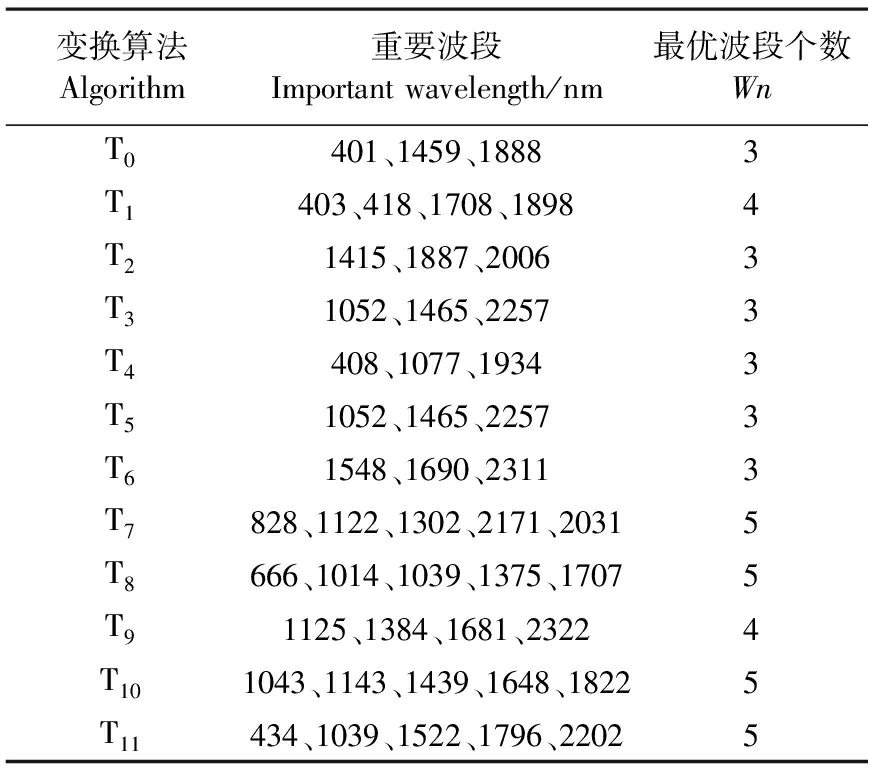
表2 基于SPA和不同光谱变化方法的重要波段的提取

2.3 基于SPA-MLR方法的土壤含水量光谱预测模型建立

以原始光谱以及11种变换后基于SPA提取的特征波段为自变量，以土壤含水量为因变量，利用MLR建立的土壤含水量高光谱预测模型，如表3所示。基于11种变换处理建立的SPA-MLR模型监测精度，除了T3比较低外，其余变换均优于原始光谱所建的模型，表明原始光谱经一定数学变换处理可以提高土壤含水量高光谱监测精度。T6、T7、T8、T9、T10、T11的监测模型精度均高于对应的一阶微分处理前T0、T1、T2、T3、T4、T5。表明一阶微分变换能提高土壤含水量模型的精度。在所有数学变换中，T8的校正模型的监测效果最好，其决定系数R2和RPD最大，分别达到了0.957和4.74，RMSE最小，为2.16。T11次之，其R2和RPD分别达到了0.944和4.15，RMSE为2.55。T3的校正模型监测效果最差，R2和RPD都最低，分别为0.860和2.31，RMSE最大，为6.18。

表3不同土壤含水量光谱预测模型

Tab. 3 Predictive models of different soil moisture content

变换算法Algorithms模型ModelsR2RMSE/%RPDT0y=417.660R401-415.185R1888+271.944R1459+19.3910.8873.632.79T1y=0.694R403+0.100R418-13.925R1708+6.812R1898+13.7530.9003.423.03T2y=312.330R1415-304.339R1887+13.2570.9183.103.37T3y=225.499R1465-178.004R1052-67.516R2257-27.9320.8606.182.31T4y=-332.373R1934-29.668R408+452.190R1007-62.9350.9152.484.36T5y=46.633R1898-79.946R1708+5.419R403+37.6670.9202.893.65T6y=108790.163R1548-92439.173R1690-10313.521R2311-0.6110.9422.614.02T7y=1720.981R1302-1389.581R828+253.218R2171-1976.432R1122-612.636R2031+1.2500.9142.793.78T8y=629.471R666+8158.075R1014-12587.075R1039-31671.078R1375+34808.678R1707-2.1520.9572.164.94T9y=14294.340R1384-3194.977R2322+8246.352R1681-1491.601R1125-12.9010.9436.114.74T10y=-123683.801R1439+11675.161R1648-18882.797R1043-9774.030R1822-6604.232R1143+19.1850.9353.943.82T11y=-9208.900R1522-4388.004R1796-2637.737R1039+3034.038R2202+137.782R434-2.1220.9442.554.15

2.4 模型精度验证

利用验证集样本对土壤含水量预测模型分别进行验证。原始光谱以及11种变换后基于SPA-MLR建立的土壤含水量监测模型验证结果如表4所示。从表中可看出，所有数学变换处理后模型的验证效果均优于原始光谱建立的模型，其中T8变换模型精度最高。为了更直观地展示模型精确度，以T8为例制作预测值与实测值1∶1关系图(图2)。由图可以看出,T8处理模型的拟合效果较好，其验证集R2最大为0.903，RMSE最小为3.41，RPD较大为2.95。

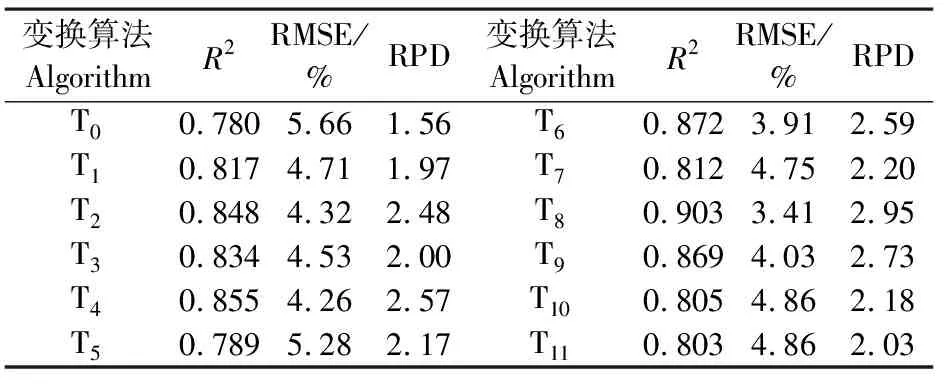
表4 模型验证结果

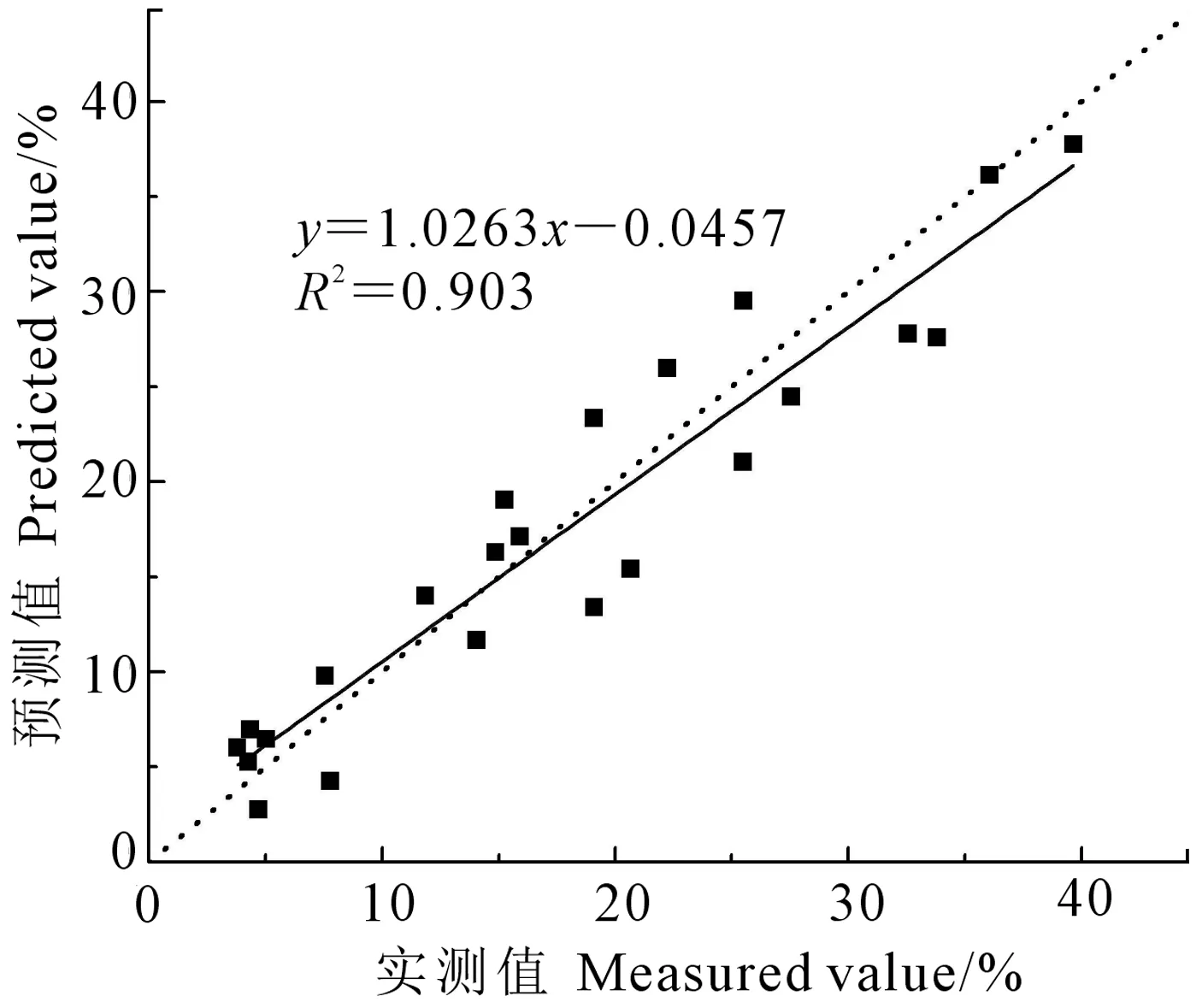
图2 土壤含水量实测值与估测值1∶1图Fig.2 The correlation between predicted values and measured values of soil water content

3 讨 论

光谱数据变换可以有效地消除土壤光谱噪音和背景的影响，放大特征光谱信息。本研究选择11种典型的变换算法对土壤光谱进行变换，然后使用连续投影算法(SPA)提取特征波段，结合MLR建立土壤含水量光谱监测模型，比较选择土壤含水量光谱监测最佳模型。有研究表明，特征波段选取个数为3～5个最佳，这样不但可以准确地表达出待测指标的信息，而且可以有效避免过拟合现象的出现[16]。本研究利用SPA提取的特征波段个数均为3～5个，所以不用再对特征波段进一步筛选。

从本研究建立的土壤含水量的校正模型及其验证结果可知，各变换处理后建立的模型都有较高的预测精度，其R2都高于0.7。其中除了T3外，各变换处理后建立的土壤含水量光谱预测模型都优于原始光谱T0，表明数学变换能提高土壤含水量模型的预测精度。这主要是由于变换处理有效地减小了光谱信息中噪音和背景的影响，放大了特征光谱信息，有利于光谱信息的提取和挖掘[17]。目前，在作物冠层和土壤光谱研究中，已经证明一阶微分处理能有效提高模型的预测精度[18,19]，在本研究中光谱一阶微分变换建立的模型表现也比较好，仅次于反射率对数一阶微分变换T8。由于土壤光谱受土壤质地、有机质含量、土壤颗粒大小等的影响较大，不同土壤的有机质含量和质地差别较大[20]。由于本试验是在单一土壤质地和有机质含量背景下完成的，因此反射率对数一阶微分T8变换能否适用于其它背景条件下(不同质地、有机质含量等)的土壤光谱还有待进一步的研究。

4 结 论

本文以人工模拟72个不同含水量的土壤样本为研究对象，测定室内光谱以及对应的土壤含水量，基于11种常见的数学变换算法，建立土壤含水量的SPA-MLR光谱监测模型，综合比较分析模型校正集和验证集模型精度评价指标(R2、RMSE、RPD)得出：各光谱变换建立的模型都有较好的预测精度，其中，反射率对数的一阶微分T8建立的模型表现最好，校正集(R2=0.957，RMSE=2.16，RPD=4.74)和验证集(R2=0.903，RMSE=3.41，RPD=2.95)表现均最好。因此反射率对数一阶微分变换处理后建立的SPA-MLR模型为土壤含水量高光谱监测最佳模型。

参考文献：

[1] Yin Z, Lei T, Yan Q, et al. A near-infrared reflectance sensor for soil surface moisture measurement[J]. Computers and Electronics in Agriculture, 2013, 99: 101-107.

[2] 孙越君, 郑小坡, 秦其明, 等. 不同质量含水量的土壤反射率光谱模拟模型[J]. 光谱学与光谱分析, 2015,35(8): 2236-2240.

[3] Stenberg B, Rossel R A V, Mouazen A M,et al. Chapter five-visible and near infrared spectroscopy in soil science[J]. Advances in Agronomy, 2010,107: 163-215.

[4] 王磊, 白由路, 卢艳丽, 等. 光谱数据变换对玉米氮素含量反演精度的影响[J]. 遥感技术与应用, 2011,26(02): 220-225.

[5] 乔星星, 冯美臣, 杨武德, 等. 变换光谱数据对土壤氮素PLSR模型的影响研究[J]. 地球信息科学学报, 2016,18(8): 1123-1132.

[6] Kemper T, Sommer S. Estimate of heavy metal contamination in soils after a mining accident using reflectance spectroscopy[J]. Environmental Science & Technology, 2002,36(12): 2742-2747.

[7] 何挺, 王静, 程烨, 等. 土壤水分光谱特征研究[J]. 土壤学报, 2006，43(6): 1027-1032.

[8] 尹业彪, 李霞, 赵钊, 等.沙质土壤含水率高光谱预测模型建立及分析[J]. 遥感技术与应用, 2011,26(3): 355-359.

[9] 谢伯承. 基于高光谱遥感不同发生层土壤的光谱信息的提取研究[D]. 杨凌：西北农林科技大学，2004.

[10] 姚艳敏, 魏娜, 唐鹏钦, 等. 黑土土壤水分高光谱特征及反演模型[J]. 农业工程学报, 2011,27(8): 95-100.

[11] 张俊华, 贾科利. 典型龟裂碱土土壤水分光谱特征及预测[J]. 应用生态学报, 2015,26(3): 884-890.

[12] Araújo M C U, Saldanha T C B, Galvao R K H, et al. The successive projections algorithm for variable selection in spectroscopic multicomponent analysis[J]. Chemometrics and Intelligent Laboratory Systems, 2001,57(2): 65-73.

[13] 陈斌, 孟祥龙, 王豪. 连续投影算法在近红外光谱校正模型优化中的应用[J]. 分析测试学报, 2007,26(1): 66-69.

[14] Galvão R K H, Araújo M C U, Silva E C,et al. Cross-validation for the selection of spectral variables using the successive rojections algorithm[J]. Journal of the Brazilian Chemical Society, 2007,18(8): 1580-1584.

[15] 刘秀英, 王力, 宋荣杰, 等. 黄绵土风干过程中土壤含水率的光谱预测[J]. 农业机械学报, 2015,46(4): 266-272.

[16] 高洪智, 卢启鹏, 丁海泉, 等. 基于连续投影算法的土壤总氮近红外特征波长的选取[J]. 光谱学与光谱分析, 2009,29(11): 2951-2954.

[17] 鲁如坤. 土壤农业化学分析方法[M]. 北京: 中国农业科技出版社,2000.

[18] 王强, 易秋香, 包安明, 等. 基于高光谱反射率的棉花冠层叶绿素密度估算[J]. 农业工程学报, 2012,28(15): 125-132.

[19] Brown D J, Shepherd K D, Walsh M G,et al. Global soil characterization with VNIR diffuse reflectance spectroscopy[J]. Geoderma, 2006,132(3): 273-290.

[20] Muller E, Decamps H. Modeling soil moisture reflectance[J]. Remote Sensing of Environment, 2001,76(2): 173-180.