一类疟疾传播模型的稳定性和后向分支
殷红燕
(中南民族大学 数学与统计学学院,武汉430074)
疟疾是一种由疟原虫引起的虫媒传染病,严重危害了人类的健康. 利用数学模型来研究传染病的流行原因及控制方法已被证实是有效的. 自从1911年,Ross发表了第一篇关于疟疾传播的数学模型的论文[1]以来,很多专家和学者在疟疾传播模型的研究上做了大量的工作,并取得了一定的成果[2-6]. 本文建立了一个简单的关于疟疾传播的SIS-SI模型,分析了模型无病平衡点的局部渐近稳定性和全局渐近稳定性,得出了基本再生数公式,讨论了地方病平衡点的存在性,并证明了后向分支的存在性.
1 模型的建立

根据以上的参数及假设,建立如下的疟疾传播模型:
(1)
注意到,所有蚊子的数量满足下面的Logistic方程:
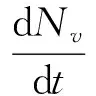
(2)
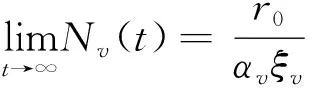
(3)

2 无病平衡点和基本再生数
特征方程为:
(λ+r0)(λ+μh)[λ2+(σh+μv)λ+σhμv-
(4)
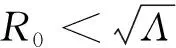
这里σh=μh+δh+θh. 显然,当:
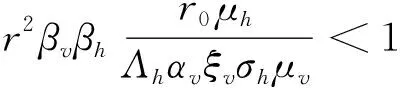
3 地方病平衡点和后向分支

(5)


(6)

(7)

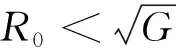

(8)


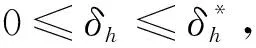

(9)
为了方便,记Sh=x1,Ih=x2,Iv=x3,并引入向量符号x=(x1,x2,x3)T和f=(f1,f2,f3)T,则方程组(9)可以写成:

(10)
这里

因此,它的特征根是λ1=-μh,λ2=-(σh+μh)和λ3=0.

为了计算文[9]中的定理4.1中定义的系数a和b,先计算f在E0的二阶偏导数:
f在E0的其他二阶偏导数都等于0. 于是:

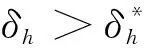

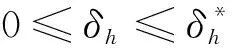
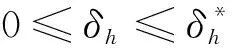
4 无病平衡点的全局渐近稳定性
关于无病平衡点E0的全局渐近稳定性,有如下的结果.

(11)



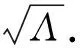
推论1 当δh=0时,如果R0<1,那么方程组(3)的无病平衡点E0是全局渐近稳定的.
5 数值模拟
本节给出两个数值例子来证实前面的一些理论结果.
例1 选取参数αv=10,μv=0.49,ξv=0.03,Λh=1000,μh=3.7,θh=0.05,δh=2.8,βh=0.59,βv=0.6,r=10. 计算可得方程组(3)的基本再生数R0≈1.1107>1,因此存在唯一的局部渐近稳定的地方病平衡点. 当t→∞时,方程组(3)的解趋近于这个地方病平衡点,如图1所示.
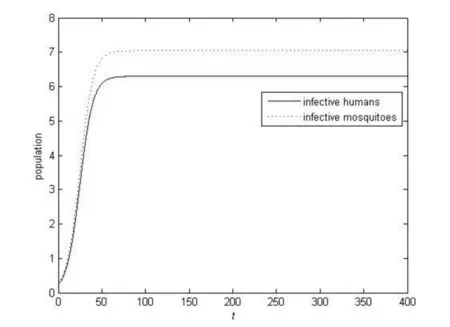
图1 当R0>1时,方程组(3)存在唯一的稳定的地方病平衡点Fig.1 System (3) has a unique stable endemic equilibrium when R0>1
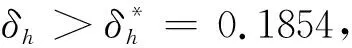
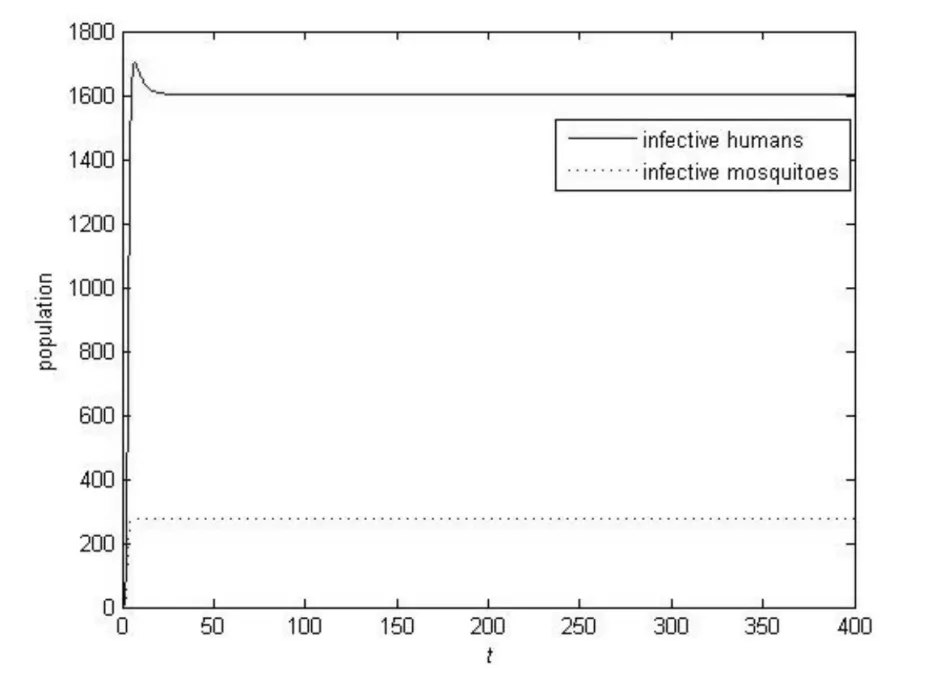
图2 当R* 图3 当R0 参 考 文 献 [1] Ross R. The prevention of malaria[M]. London: Murry, 1911: 15-20. [2] Macdonald G. The epidemiology and control of malaria[M]. London: Oxford Univ,1957: 51-62. [3] Bailey N. The biomathematics of malaria[M]. London: Charles Griff,1982: 22-30. [4] Aron J L, May S M. The population dynamics of malaria[C]//Anderson R M. Population Dynamics of Infectious Diseases: Theory and Applications.London: Chapman and Hall, 1982: 139-189. [5] Koella J C. On the use of mathematical models of malaria transmission[J]. Acta Trop, 1991, 49(1):1-25. [6] Ngwa G A. Modelling the dynamics of endemic malaria in growing population[J]. Discr Cont Dyn Syst B,2004, 4(4): 1173-1202. [7] Li Jia.New revised simple models for interactive wild and sterile mosquito populations and their dynamics[J]. Journal of Biological Dynamics, 2017, 11(2): 1-18. [8] Garba S M, Safi M A, Gumel A B. Cross-immunity-induced backward bifurcation for a model of transmission dynamics of two strains of influenza[J]. Nonlinear Anal RWA, 2013, 14(3): 1384-1403. [9] Castillo-Chavez C, Song B. Dynamical models of tuberculosis and their applications[J]. Math Biosci Eng, 2004,1(2): 361-404. [10] Hale J K. Ordinary differential equations[M]. New York: Wiley, 1969:248-249.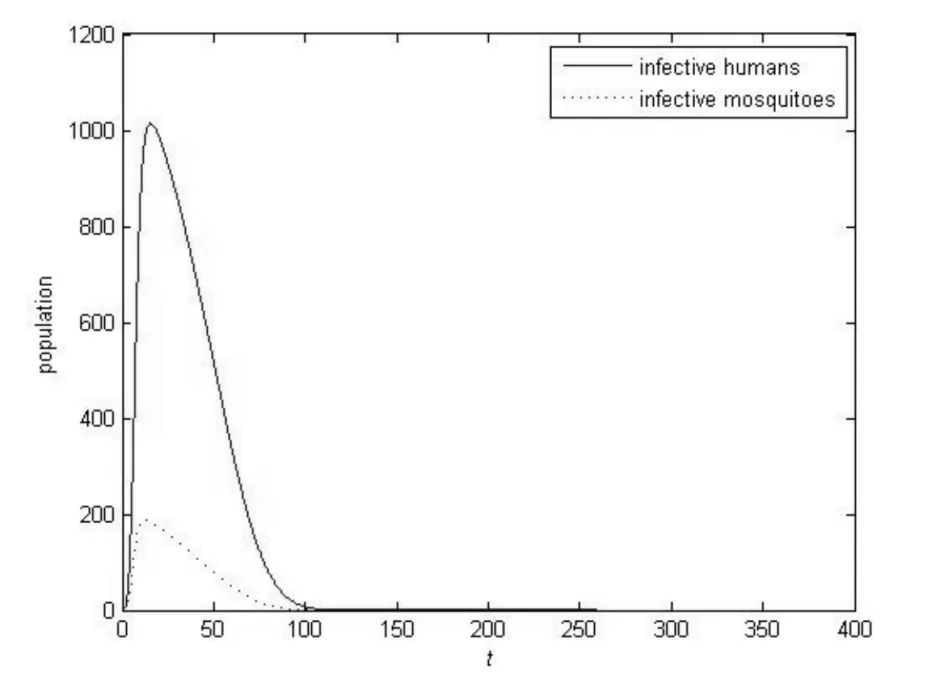
6 结语