一种标记粒化集成的多标记学习算法

李 峰，苗夺谦，张志飞，罗 晟

(同济大学 计算机科学与技术系，上海 201804)

(同济大学 嵌入式系统与服务计算教育部重点实验室，上海 201804)

1 引 言

现实世界存在的大量事物同时拥有多个标记，例如，一首乐曲可能同时包含悲伤、静谧等多种情感[1]；一个蛋白质可能同时拥有转录、新陈代谢等多种功能[2]；一幅图片可能表达了大海、沙滩等多个语义信息[3]；一部电影可能同时属于动作、喜剧等多个题材类型.这些拥有多个标记的事物称为多标记样本，这些多标记样本构成了多标记数据.然而传统机器分类学习中通常每个样本仅被赋予一个类别标记，称作单标记学习，不能直接用于多标记数据.不同于传统机器学习算法，给定一个标记空间L，多标记学习算法旨在学习标记已知的多标记数据，预测出未标记样本相关的标记子集Y，其中Y⊆L，并且|Y|≥1[4-6].

多标记数据中标记之间往往存在一定的相关性，如一部电影如果标记为“动作”类型，那么它同时属于“冒险”类型的可能性比它同时属于“爱情”类型的可能性大得多，因此在多标记学习中不能忽略标记之间的相关性.多标记数据中的样本可能同时拥有多个标记，导致了多标记数据的复杂多变，并且标记之间具有相关性，这些都极大地增加了多标记学习算法预测的难度.多标记分类问题俨然成为一个比较有挑战的问题，吸引了越来越多学者的关注与研究，成为机器学习中一个研究热点.针对多标记分类问题，一系列多标记学习算法被提出，这些算法主要可以分为两类，问题转化型方法(Problem Transformation Methods)和算法适应型方法(Algorithm Adaption Methods)[4].

第一种类型的方法独立于算法，将多标记分类问题转换成一个或者多个单标记分类问题，再利用已有的单标记学习算法处理.而第二类方法则是对某一具体算法进行改进以使其能直接处理多标记分类问题，如支持向量机(SVM)[7，8]、决策树[9，10]、神经网络[11]、粗糙集[12]、k-近邻算法[13，14]等.本文主要研究第一类方法.

本文基于粒计算的思想，提出了一种标记粒化集成的多标记学习算法(Label-Granulated Ensemble Method for Multi-label Learning，GEM).粒计算(Granular Computing，GrC)[18，19]是目前解决复杂问题的有效方法之一，其模拟人类处理复杂问题的方式，将复杂问题转化为若干简单问题，依据某一特性从信息或者数据中抽象出信息粒.该方法为标记空间中的每一个标记找到相关性程度最大的前k个标记，这k个标记构成了一个关系粒，这样使标记间的相关性最大可能地被考虑.对每一个关系粒构建一个分类器，最后集成各分类器的结果，最终输出预测的结果.GEM算法不仅考虑到了标记之间的相关性，而且根据标记之间的相关性构建关系粒，避免了LP算法复杂度过高、泛化性不够的问题和RAkEL方法随机选择造成的不稳定性，以及标记可能被遗漏的，算法性能不够好的问题.

在三个多标记数据集上通过实验研究了关系粒的基数，既标记个数对算法性能的影响.并跟BR方法、LP方法和RAkEL方法进行了比对.实验表明本文所提算法能取得较好的性能.

本文在第一部分介绍了本文工作提出的背景；相关的基础知识放在了第二部分；第三部分详细介绍了本文所提算法；在第四部分通过实验验证了本文所提算法的有效性；最后对本文工作进行了总结.

2 基础知识

这里先简要介绍与本文所提算法相关的基础知识，多标记学习和互信息的基本概念.

2.1 多标记学习

给定一个b维的样本空间F=Rb和q个标记的标记空间L.T={(X1，Y1)，(X2，Y2)，…，(Xn，Yn)}表示一个多标记数据集，其中每个样本Xi∈F表示为一b维特征向量，Yi={yi1，yi2，…，yiq}表示样本Xi对应的标记向量，当Xi含有标记lj时，yij=1，否则yij=0(1≤i≤n，1≤j≤q).

2.2 互信息

定义1. 熵[20，21]能有效地度量随机变量不确定性，随机变量A的熵定义为：

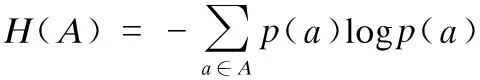
(1)

其中，p(a)表示a的概率密度.

定义2. 给定变量A时变量C的条件熵为：

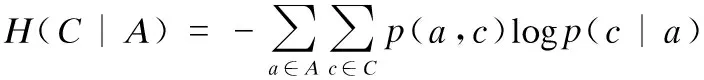
(2)

其中p(a，c)是联合概率密度，p(c|a)是条件概率密度.

定义3. 互信息能度量两个变量间相互依赖的程度，变量A和C的互信息定义为：

(3)

从式(3)可以看出MI(A；C)=MI(C；A).

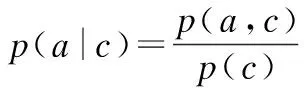
MI(A；C)=H(A)-H(A|C).

(4)

3 粒化集成多标记学习算法

针对LP算法复杂度过高，RAkEL方法稳定性不佳的问题，以及粒计算能较好的把复杂问题转化为若干简单问题，本文提出了一种标记粒化集成的多标记学习算法.该算法首先根据标记之间的相关性，为每个标记li∈L划分出一个与之相关度最大的k个标记构成的标记子集，记为关系粒[li]k.将标记之间的相关性考虑进标记子集的划分中，相较于RAkEL方法更加直接而且稳定.对每一个关系粒[li]k构建一个分类模型，对于∀lj∈[li]k有hi：X→lj，lj，预测出在该分类模型下样本X是否含有标记lj，模型可改写为输出预测值hi(X，lj)，如果X含有lj则hi(X，lj)=1，否则hi(X，lj)=0.最终对各分类模型的相应预测的值集成后输出预测的标记向量Y′.算法流程如图1所示.

图1 粒化集成算法流程Fig.1 Flowchart of the proposed method

3.1 关系粒

定义4. 给定一个标记li∈L和相关度度量函数S，那么li的关系粒[li]k定义为：

[li]k={lj|Rank(S(li，lj))≤k，lj∈L}

(5)

其中，k为关系粒基数，确定了关系粒中标记的个数，满足1≤k≤q，Rank(σ)为排序函数，其对σ值从大到小排序.对于∀li，lj∈L，满足以下性质：

1)0≤S(li，lj)≤1；

2)S(li，lj)=S(lj，li)；

3)Rank(S(li，li))=1.

从定义4可以看出当关系粒基数k=q时，关系粒与标记空间等同，所有的标记组合被考虑，则是LP方法.然而当k=1时，关系粒中只剩自身一个标记，不考虑标记之间的相关性，则是BR方法.更进一步，当k=q或k=1时，轻易可以看出关系粒[li]k为等价类.

相关度度量函数S影响着关系粒中标记的选择.在机器学习中，常用各类距离函数度量不同样本间的相关性，如欧氏距离、曼哈顿距离、马氏距离等.在多标记学习中，也常用各类相关性度量函数来判断样本间的相关性，但相较于传统机器学习，多标记学习还度量标记间的相关性.常见的标记间相关性度量函数有基于互信息的相关性度量，基于皮尔逊相关系数的相关性度量.基于距离函数的相关性度量往往只能度量正相关性，不能很好地判断负相关性.而互信息是常用的度量两个变量相关性的有效方式之一，不仅能度量正相关性，还能评估非线性相关性和负相关性，所以这里我们选用常用的互信息定义两个标记间的相关性，作为相关度度量函数.给定∀li，lj∈L，根据公式(3)他们间的相关性计算如下：

S(li，lj)=MI(li；lj)

(6)

由定理1，相关性度量函数可表示为：

S(li，lj)=H(li)-H(li|lj)

(7)

从式(7)可以看出，对于给定的一个标记li，H(li)为常数，对排序函数Rank(σ)而言，去除或者添加一个常数项，对排序结果无影响.因此求解关系粒[li]k对相关性度量函数S(li，lj)的排序可转换为只由条件熵表示即：

Rank(S(li，lj))∝Rank(-H(li|lj))

定义4中关系粒[li]k的求解可改写为：

[li]k={lj|Rank(-H(li|lj))≤k，lj∈L}

(8)

既对已知标记lj，标记li存在的不确定性大小的负值进行排序，不确定性越小说明相关度越大.关系粒的划分过程伪代码如算法1所示.

算法1.标记粒化算法

输入：标记空间L，关系粒基数k，训练集T={(X1，Y1)，(X2，Y2)，…，(Xn，Yn)}

输出：关系粒[li]k，1≤i≤q

第1步：

Fori=1：q

//初始化关系粒

①[li]k←φ；

②Forj=1：q

根据公式(2)计算条件熵H(li|lj)，(li，lj∈L)；

End For

③Car←k；

④WhileCar>0

a)查找条件熵最小的标记arg min1≤a≤qH(li|la)；

b)[li]k←la；

c)H(li|la)←∞；

d)Car←Car-1；

End While

End For

第2步：得到关系粒[li]k，1≤i≤q.

3.2 分类器

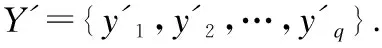
算法2.粒化集成多标记学习算法

输入：未标记样本X，关系粒基数k，训练集T={(X1，Y1)，(X2，Y2)，…，(Xn，Yn)}，标记空间L

输出：未标记样本X对应的标记向量Y′

第1步：

调用算法1；

第2步：

Forj=1：q

训练分类模型hi；

Negj←0；

Posj←0；

End For

第3步：

Fori=1：q

Forlj∈[li]k

Negj←Negj+1-hi(X，lj)；

Posj←Posj+hi(X，lj)；

End For

End For

第4步：

Forj=1：q

IfPosj≥Negj

yj←1；

Else if

yj←0；

End If

End For

第5步：输出预测的标记向量Y′

4 实验分析

4.1 数据集及实验设置

本文从Mulan Library[22]选取了3个涵盖文本、图像、生物的来自真实世界的多标记数据集进行了实验，以验证本文所提算法的有效性.数据集的详细信息如表1所示.表中，样本数是指该数据集包含的样本数量，特征数是指特征空间的维度，标记数则是该数据集标记空间的标记个数，标记基数是平均每个样本所含有的标记数量.

Scene数据集[15]包含2407张图片，每张图片由6个可能的语义标记标注.其特征空间由294维视觉特征构成.

Medical数据集[23]是关于病例诊断的数据里.该数据集包含了978个病历文本记录样本，每个样本由1449维的诊断历史记录和观察到的症状组成，标记空间则是45种ICD-9-CM疾病编码.

Yeast数据集[7]用于描述酵母菌的基因功能分类，由2417个yeast基因样本和14种可能的基因功能构成.每个基因样本对应于一个103维的特征向量.

为了验证算法的性能，实验中将所提算法与BR方法、LP方法和RAkEL方法进行了比对.根据文献[16]建议的参数配置，RAkEL方法的子集大小为2，子集数量为2p，阈值设为0.5.支持向量机算法(SVM)是机器学习中的经典算法，能有效地处理多类分类问题，因此本文选取了RBF核的支持向量机算法构建最终的分类模型，损失参数取1，gamma值为0.07.实验采用了十折交叉验证方法(Ten-foldcross-validation).

表1 多标签数据集Table 1 Multi-label datasets used in the experiments

4.2 评价指标

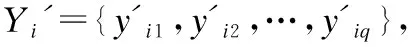
汉明损失度量算法预测出的标记信息与实际的标记信息的平均差异值.

当π条件满足时，<π> 值为1，否则为0.该指标值越小说明算法性能越好.

综合评价指标F1值是准确率和召回率的调和平均值，解决了准确率和召回率可能存在矛盾的问题，是机器学习中常用的一个评价指标.当我们知道真正数tp，真负数tn，假正数fp，假负数fn，那么F1的计算如下：

微平均F1与宏平均F1是以两种不同的平均方式求的全局的F1指标.微平均F1和宏平均F1能综合多个类别的分类情况，评测系统整体性能.给定标记li的tpi、tni、fpi和fni四个值，那么MicroF1和MacroF1计算如下：

微平均F1与宏平均F1值越高说明算法性能越好.

4.3 实验结果及分析

4.3.1 关系粒基数选择

该部分研究了关系粒基数k的取值变化对算法性能的影响.从表1可以看出数据集Scene、Medical和Yeast标记空间的维数q分别为6、45和14标记数，当关系粒基数k取1时为BR方法，取q时为LP方法，因此在实验中我们令2≤k≤q-1.由于Medical的标记空间维数过大，当基数k取值过大时，丧失了粒化的意义，因此实验中我们对其基数取值为2≤k≤20.各评价指标结果在各数据集上随着基数k增加的变化曲线如图2-图4所示.图中显示的评价指标值为十折交叉验证的均值，为了让各评价指标结果能在图中清晰的表示，更清楚地观察变化规律，对同一数据集地单一评价指标结果进行了放大和移动，但这些修改不影响评价指标的变化规律.

从图2可以看出，在Medical数据集上，随着k的增加汉明损失先逐渐变小，微平均F1逐渐变大，当k取13时两个指标达到最优，而宏平均F1的变化较复杂，但综合考量三个评价指标，当k取13时算法在Medical数据集上最优.而从图3和图4可以清楚地看出在Scene数据集和Yeast数据集上的最优在k取5时获得.

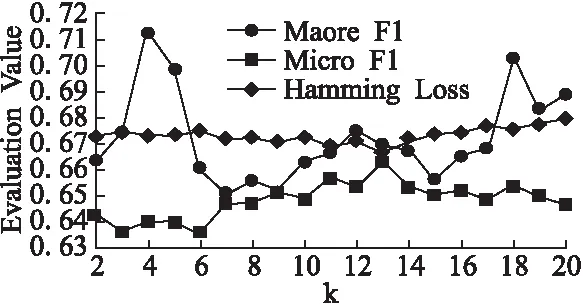
图2 Medical数据集上评价指标随着k增加变化曲线Fig.2 Evaluation criteria of varying the number of k on Medical

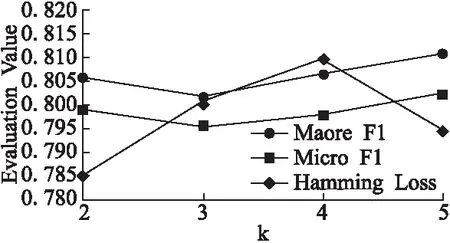
图3 Scene数据集上评价指标随着k增加变化曲线Fig.3 Evaluation criteria of varying the number of k on Scene

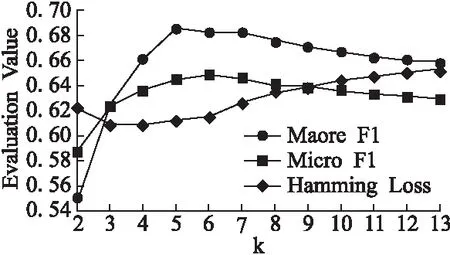
图4 Yeast数据集上评价指标随着k增加变化曲线Fig.4 Evaluation criteria of varying the number of k on Yeast

4.3.2 对比实验分析

各对比算法BR方法、LP方法RAkEL方法和本文所提算法在各数据集上的实验结果如表2所示.表中↑(↓)符号表示该项指标值越大算法性能越好.

从表2可以看出在Medical数据集上，各个对比算法取得的Hamming Loss值比较相近，GEM在MicroF1指标上优于其它三个算法，而LP方法在MacroF1上取得最优，但跟本文所提算法GEM相差不大.本文所提算法在数据集Scene上各项指标均优于其它对比算法，但在Hamming Loss上跟其它算法差异较小.BR算法性能明显劣于其它.Yeast数据集中，从MicroF1和MacroF1两项指标来看GEM最优，从Hamming Loss角度，除了LP外，其它三种方法所取得的结果差异较小.从三个数据集整体上看，本文所提算法性能整体上优于其它三种算法.

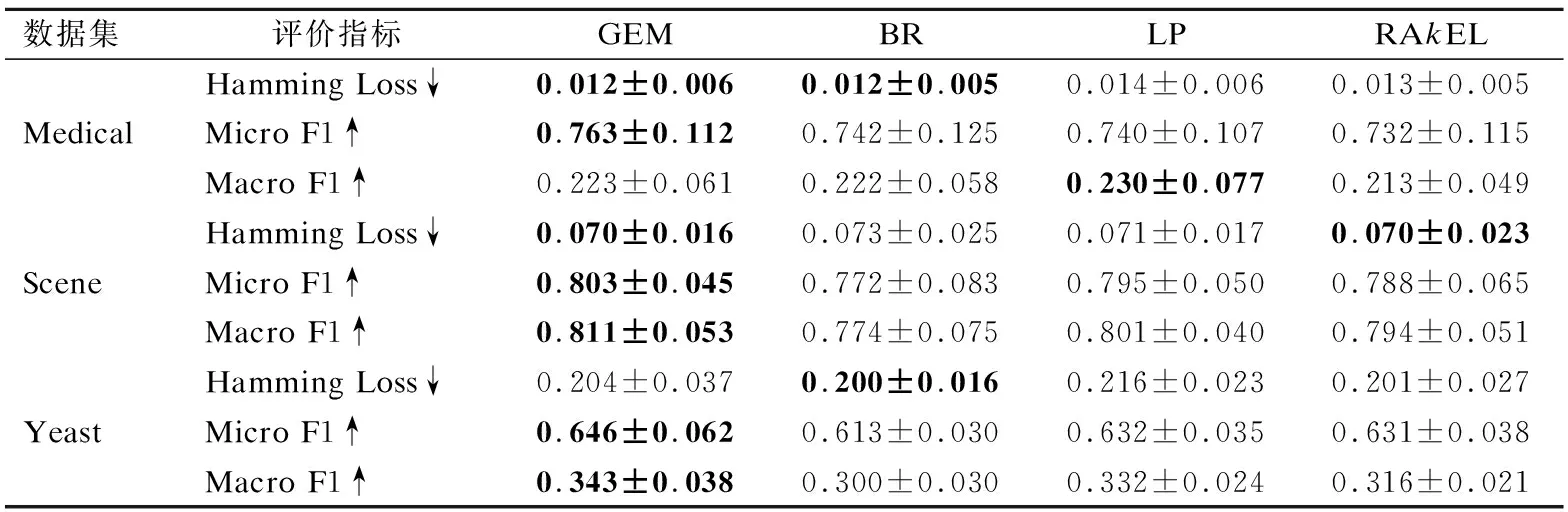
表2 对比实验结果(均值±标准差)Table 2 Compared experimental results (mean±std.deviation)

5 结 论

针对BR方法忽略标记间的相关性，LP算法复杂度过高、标记组合对应的正例可能过少的问题，RAkEL方法中随机选择子集造成算法性能不稳定的问题，本文提出了一种粒化集成的多标记学习算法.该算法根据标记间的相关性，为每一个标记找到一个关系粒，考虑关系粒中标记组合，构建一个单标记分类器，最终集成各分类器的结果.能避免前面提到的问题，产生稳定较好的结果.实验结果表明相较于其它对比算法，本文所提算法能取得较好的预测效果.

：

[1] Tsoumakas G，Katakis I，Vlahavas I.Multi-label classification of music into emotions[C].Proceedings of the 9th International Conference on Music Information Retrieval，Philadephia，ISMIR 2008：325-330.

[2] Yu Ying，Pedrycz W，Miao Duo-qian.Neighborhood rough sets based multi-label classification for automatic image annotation[J].International Journal of Approximate Reasoning，2013，54(9)：1373-1387.

[3] Pavlidis P，Weston J，Cai J，et al.Grundy.Combining microarray expression data and phylogenetic profiles to learn functional categories using support vector machines[C] .Proceedings of the 5th Annual International Conference on Computational Biology，Montreal，QC：ACM，2001：242-248.

[4] Tsoumakas G，Katakis I，Vlahavas I.Mining multi-label data/Data mining and knowledge discovery handbook[M].Berlin：Springer，2010：667-685.

[5] Tsoumakas G，Katakis I.Multi label classification：An overview[J].International Journal of Data Warehousing and Mining，2007，3(3)：1-13.

[6] Zhang Min-ling，Zhou Zhi-hua.A Review on multi-label learning algorithms[J].IEEE Transactions on Knowledge and Data Engineering，2014，26(8)：1819-1837.

[7] Elisseeff A，Weston J.A kernel method for multi-labelled classification[C].Proceedings of Advances in Neural Information Processing Systems，Vancouver，BC：NIPS，2001：681-687.

[8] Chen W J，Shao Y H，Li C N，et al.MLTSVM：a novel twin support vector machine to multi-label learning[J].Pattern Recognition，2015，52：61-74.

[9] Clare A，King R.Knowledge discovery in multi-label phenotype data[G].LNCS 2168：Proceedings of the 5th European Conference on Principles of Data Mining and Knowledge Discovery：PKDD 2001.Berlin：Springer，2001：42-53.

[10] Wu Q，Tan M，Song H，et al.ML-forest：a multi-label tree ensemble method for multi-label classification[J].IEEE Transactions on Knowledge and Data Engineering，2016，28(10)：2665-2680.

[11] Zhang Min-ling，Zhou Zhi-hua.Multi-label neural networks with applications to functional genomics and text categorization[J].IEEE Transactions on Knowledge and Data Engineering，2006，18(10)：1338-1351.

[12] Yu Ying，Pedrycz W，Miao Duo-qian.Multi-label classification by exploiting label correlations[J].Expert Systems with Applications，2014，41(6)：2989-3004.

[13] Zhang Min-ling，Zhou Zhi-hua.ML-kNN：a lazy learning approach to multi-label learning[J].Pattern Recognition，2007，40(7)：2038-2048.

[14] Zhang Min-ling.An improved multi-label lazy learning approach[J].Journal of Computer Research and Development，2012，49(11)：2271-2282.

[15] Boutell M，Luo J，Shen X，et al.Learning multi-label scene classification[J].Pattern Recognition，2004，37(9)：1757-1771.

[16] Tsoumakas G，Katakis I，Vlahavas I.Randomk-labelsets for multilabel classification[J].IEEE Transactions on Knowledge and Data Engineering，2011，23(7)：1079-1089.

[17] Tsoumakas G，Vlahavas I.Random k-labelsets：An ensemble method for multilabel classification[M].Machine Learning：ECML′07，Springer，Berlin，2007，406-417.

[18] Yao Yi-yu.Interpreting concept learning in cognitive informatics and granular computing[J].IEEE Transactions on Systems，Man，and Cybernetics，Part B：Cybernetics，2009，39(4)：855-866.

[19] Yao Yi-yu，Zhao Li-quan.A measurement theory view on the granularity of partitions[J].Information Sciences，2012，213(23)：1-13.

[20] Shannon C.A mathematical theory of communication[J].Bell System Technical Journal，1948，27(3)：379-423.

[21] Shannon C.A mathematical theory of communication[J].Bell System Technical Journal，1948，27(4)：623-656.

[22] Tsoumakas G，Spyromitros-Xiousfis E，Vilcek I.Mulan：a java library for multi-label learning[J].Journal of Machine Learning Research，2011，12(7)：2411-2414.

[23] Pestian J，Brew C，Matykiewicz P，et al.A shared task involving multi-label classification of clinical free text[C].Proceedings of the Workshop on BioNLP 2007：Biological，Translational，and Clinical Language Processing，Prague：BioNLP，2007：97-104.

附中文参考文献：

[14] 张敏灵.一种新型多标记懒惰学习算法[J].计算机研究与发展，2012，49(11)：2271-2282.